仰斜式挡土墙稳定影响因素分析

夏智翼

（国网新源水电有限公司丰满培训中心，吉林省吉林市 132108）

仰斜式挡土墙稳定影响因素分析

夏智翼

（国网新源水电有限公司丰满培训中心，吉林省吉林市 132108）

在许多工程中，挡土墙的安全与整个工程的安全是息息相关。由于仰斜式挡土墙的受力较好，在工程中得以广泛应用。但目前针对仰斜式挡土墙的相关设计说明及算例较少，对作用在挡土墙上土压力的计算不够合理，造成挡土墙的开裂及失稳等问题。本文针对上述存在的问题，对仰斜式挡土墙的土压力、墙体应力以及稳定计算等关键问题做深入的研究和探讨。

仰斜式挡土墙；土压力；有限单元法；ABAQUS

0 引言

挡土墙被广泛应用于水利水电、铁路、公路、桥梁等工程中，主要起到安全防护的作用，挡土墙的安全不仅关系到经济效益问题，甚至还直接威胁到人民生命安全。因此，有必要对作用在挡土墙上的土压力以及边坡的稳定进行深入的分析研究[1]。

计算挡土墙稳定的关键问题是如何准确地计算出墙背及墙前的土压力。目前针对仰斜式挡土墙的相关设计说明及算例较少，挡土墙设计规范中也并没有给出适用于仰斜式挡土墙土压力的计算方法，只是建议参照重力式挡土墙的土压力计算方法——库仑理论方法来计算。库仑理论方法假定的条件和实际工程中的条件不相符合，只能采取简化条件，且计算时没有考虑仰斜式挡土墙与土体之间的相互作用以及位移协调的作用，采用这种方法计算出的结果与实际的受力情况常常存在一定偏差。由于土压力计算不准确，会造成挡土墙的安全隐患或资源浪费，因此如何准确计算仰斜式挡土墙所受的土压力，以及如何控制安全系数这两个问题的解决就显得尤为重要。

1 仰斜式挡土墙的数值模拟

1.1 工程概况

某水库位于海河流域卫河水系，总库容246万m3，是一座以防洪、灌溉为主，兼顾水产养殖等综合利用的小（Ⅰ）型水库。水库主坝为土石结构，副坝为均质土坝。典型断面坝体高5.5m，坝坡上游做浆砌石斜墙，斜墙外坡1∶0.9，内坡1∶0.7，坝脚采用1.0m深的浆砌石护角，宽度比培厚浆砌石宽0.3m。下游坝坡坡度为1∶2.5，下游水位72.30m。水库挡土墙典型断面（见图1）。

1.2 几何模型的建立

由于挡土墙沿长度方向的形式完全一致，故几何模型可简化为二维模型，不考虑坝顶防浪墙的影响，建立较规则的有限元几何模型。垂直坝轴线方向断面图如图2所示。

1.3 材料模型的选取

仰斜式挡土墙线弹性模型，选取的基本参数见下表1。

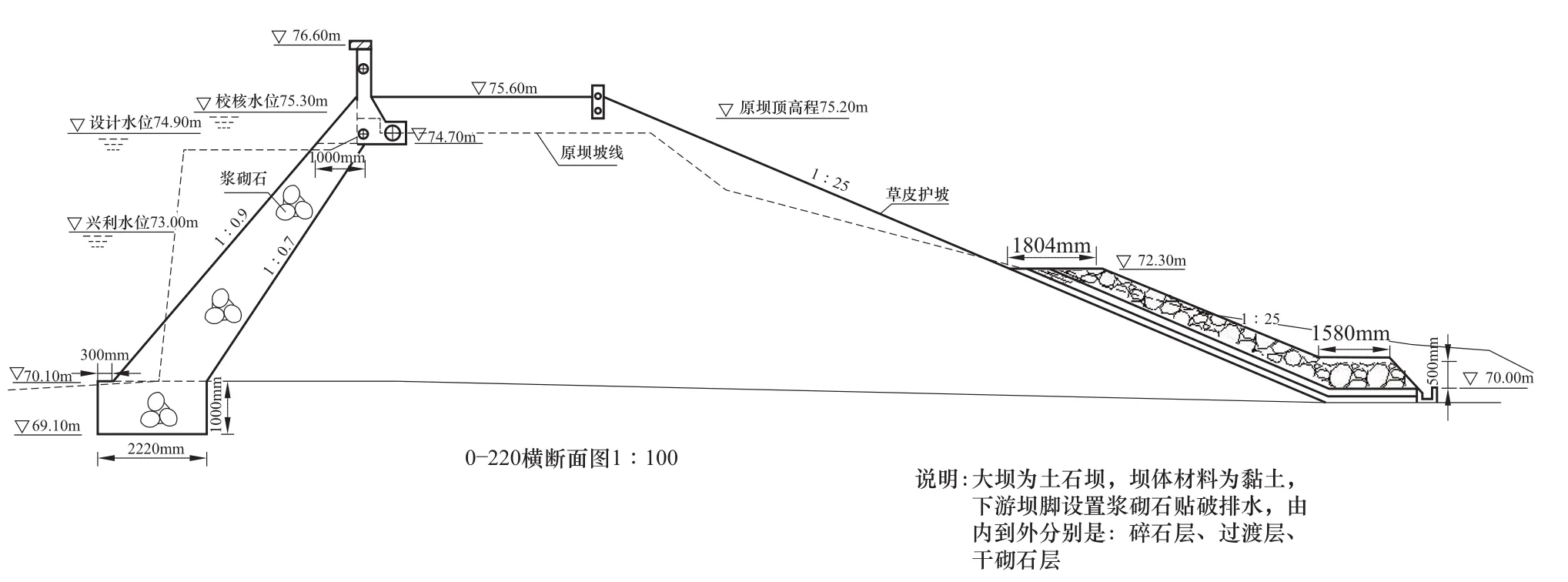
图1 计算典型断面图

图2 垂直坝轴线方向断面图

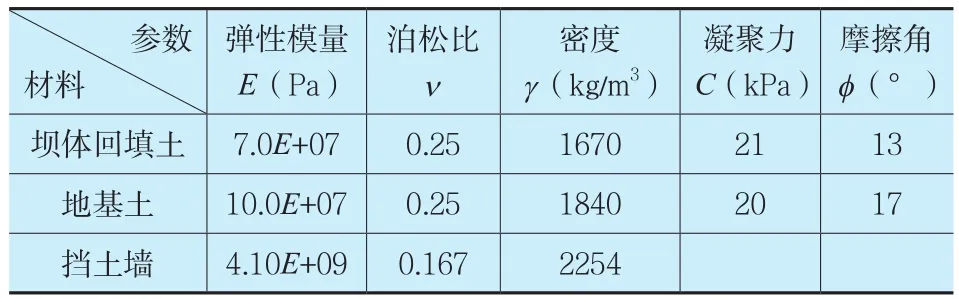
表1 模型材料参数表

1.4 荷载及边界条件

根据实际情况，在荷载施加过程中，各部件之间可能会产生接触，主要包括挡土墙墙体、挡土墙基底与土体之间的接触[2]。本文采用摩擦约束，以主从面接触对来设置其接触特性。墙体摩擦系数参照规范取为0.4。

1.5 网格划分及单元选取

有限元分析计算时，网格的尺寸等参数将极大影响计算结果，通常情况下，计算结果的精度与划分的网格数量成正比[3]。但随着网格划分得越精细，模型的计算成本也会随着增大。为了保证工程应用时尽量提高计算效率，缩短计算时间，又能够满足工程中所需达到的精度，本文根据实际情况，将与墙体接触部分对网格进行了细化处理，其余土体的网格间距逐渐增大，网格划分结果如图3所示。

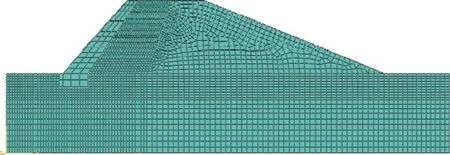
图3 几何模型网格划分

2 仰斜式挡土墙有限元计算结果分析

2.1 墙背土压力计算结果

以0+220断面建立ABAQUS有限元模型，计算后得到墙后土体的水平应力云图如图4所示，提取墙背后土体中各节点的水平力值的并将变化趋势绘成图5。

由图5可以看出，墙背上各点的土压力值呈曲线分布且存在波动。由于墙体和土体之间存在摩擦力、土体之间存在相互作用，引起沿墙体上节点力分布呈波动状态，且在距离墙底约1/3处达到最大值，与库仑土压力理论作用点位于墙底1/3处的结论基本一致。

图4 有限元模型计算结果的水平压力云图（纵轴方向表示土体水平压力，单位：Pɑ；横轴方向表示距墙顶距离，单位：m）

图5 墙背上墙顶至墙底各点土压力值分布图

2.2 墙前土压力计算结果

《挡土墙设计实用手册》建议，当挡土墙嵌入地面以下的深度在1m以内时，可忽略不计墙前被动土压力的影响；当挡土墙嵌入地面以下1m以上的深层时，通常是按主动土压力进行计算，而不按被动土压力计算；当有必要按被动土压力进行计算时，应对被动土压力计算值进行折减，即按实际计算的被动土压力的某个百分数来考虑，有文献建议取其30%～50%[1]。根据以上理论，本文的墙前土压力应按照主动土压力来计算。根据实际工程资料，分别按主动土压力以及被动土压力方法进行计算，所得到的土压力值列入表2。将用ABAQUS模拟计算所得的各节点应力积分得到土压力值也列入表2，并对两种方法的计算结果进行对比分析。

表2 理论方法与有限元方法墙前土压力计算结果

由计算结果可知，有限元软件计算出的墙前土压力略大于理论公式所求得的被动土压力的值，按照土压力理论，土体应该已经发生破坏，但是由于应力集中、计算误差等原因，在有限元计算当中，虽然总的土压力已经超过被动土压力，但墙前土体还没有发生整体破坏，然而在墙前已经产生了较大的塑性区，如图6所示，说明此时土体已经接近破坏，计算结果合理。

图6 有限元计算结果PEEQ云图

2.3 基底应力计算结果

挡土墙基底应力设计要求：通常状况下，土基不得出现拉应力，岩基不得出现非常小的拉应力，最小压应力应符合规定，最大压应力须控制在地基承载力设计值以内。

用有限元方法计算所得的挡土墙竖直方向应力云图如图7所示，并将计算所得的各节点竖向应力写入数据文件，将基底所包含节点竖向应力值整理后，将计算结果列入表3中。基底最大应力值Pmax=91.06kPa＜300kPa（满足要求），基底最小应力值Pmin=10.25kPa＞0（满足要求）。

图7 挡土墙竖直方向应力云图

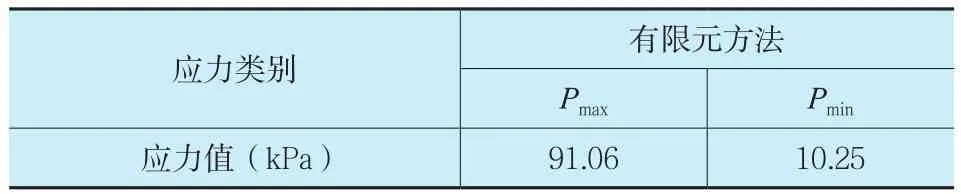
表3 有限元方法基底应力计算结果

2.4 墙身应力计算结果

墙身应力验算应选择具有代表性的墙身截面，一般来说，墙身与墙基结合面的强度若能满足，则其上各截面则均可达到要求，无需再算。参考挡土墙设计规范以及工程资料，当挡土墙偏心受压时，计算截面以上部分荷载作用偏心距需满足的条件为：砌体轴心抗压强度1.14N/mm2，砌体抗拉强度0.24N/mm2。

由有限元方法计算所得的墙身所受的压应力及拉应力如图8和图9所示。

图8 挡土墙墙身压应力云图

图9 挡土墙剪应力云图

表4 有限元方法基底应力计算结果

由表4中的有限元计算值可以看出：最大压应力值σmax=98.03kN/m2＜1140kN/m2，满足要求，σmin=-16.87kN/m2，说明此时结构中产生拉应力，但小于轴心抗拉强度0.24N/mm2，因此也是满足要求的；最大剪切应力τ=278.07kN/m2，小于抗剪允许值[τ]=0.6 N/mm2，因此也是满足要求的。

3 仰斜式挡土墙稳定影响因素分析

挡土墙墙体破坏的主要有以下方面的原因：

（1）挡土墙截面厚度不够，无法完全承受土压力。

（2）边坡排水不畅，造成土压力增大导致裂缝的产生。

（3）由于地基承载力不足或不均匀沉降而引起的破坏。

在实际工程当中，由于土体性状，墙体断面形式，墙体高度、坡度、厚度，地基深度等因素，都极大地影响着墙后的水平土压力和沉降，从而影响着挡土墙的稳定性。在实际工程中，极难将所有的影响因素统一归纳到一个理论公式当中。即使可以归纳为计算公式，也很难将理论公式广泛地应用于实际[4]。

本文分析现有的土压力计算方法，将各种方法所考虑的因素分别列于表5内。

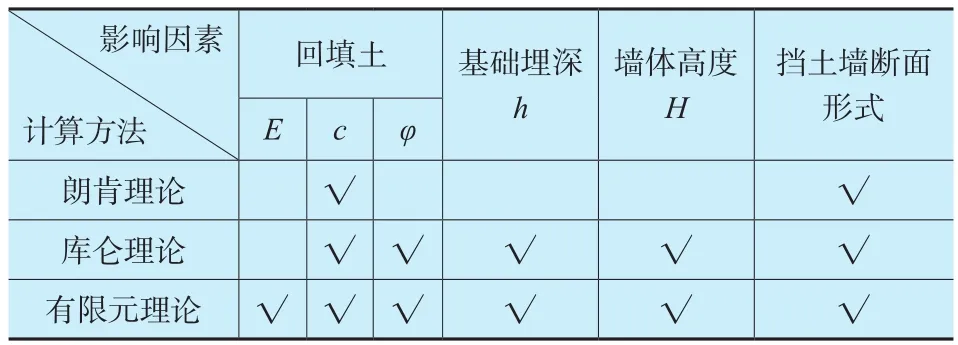
表5 各计算方法考虑因素

由上表可以看出，传统理论方法计算时忽略了土体弹模对土压力的影响，并且很少考虑基础埋深对挡土墙稳定的影响。结合本文的研究目的，为有效解决这一问题，本文考虑了以下几个影响因素：

（1）墙后填土的材料特性。

（2）墙基的埋置深度。

3.1 墙后填土的弹性模量E对土压力和安全系数的影响

由于不同地区不同性质的土体的弹性模量不同，本文针对填土弹性模量的变化对水平土压力的影响做出相应的分析研究。土体弹性模量E取值的范围通常在10～50MPa之间，本文在建立对比模型时，以原始模型参数为基础，将墙后填土弹性模量E分别取为10MPa、20MPa、…、50MPa，并保持其他参数不变，对各对比模型进行计算分析，提取沿墙体面从上至下各节点主动土压力值整理并绘制成图10：

图10 改变填土性状对各节点水平土压力的影响

从图10可以看出，位于距墙底1/3处附近的节点土压力值达到最大，与库仑理论提出的土压力作用点位于距墙底1/3处的结论基本一致。提取模型中所求得的各单元的水平力并对其积分，得到墙背上的总水平土压力值，整理后如表6所示：

表6 填土弹性模量E对水平土压力的影响

由表6可以看出，随着挡土墙后填土的弹性模量E在逐渐增大时，作用在墙体上的主动土压力水平分力在不断减小。对于同一土体来说，土体越密实，其弹模越大，土体越稳定。由此可知，在施工时，提高施工质量，保证回填土的压实度，这样可以降低墙体后的土压力，以提高挡土墙的稳定性，使挡土墙更加安全。

根据前文所计算出的各不同弹模条件下所对应的水平土压力，由安全系数公式分别计算各状况下的挡土墙抗滑安全系数和抗倾覆安全系数，计算整理后如表7和表8所示：

表7 填土弹性模量E对抗滑安全系数Ks的影响

表8 填土弹性模量E对抗倾覆安全系数Kt的影响

由表7和表8也可看出，随着弹性模量逐渐增大，抗滑安全系数与抗倾覆安全系数均逐渐增大。弹性模量在工程中可理解为墙后填土的压实程度。由此，可以提出一项对工程有指导的建议：在施工时，提高工程质量，增加墙后填土的压实度，在一定范围内有利于挡土墙的稳定。

3.2 墙后填土的等效内摩擦角对土压力和安全系数的影响

在进行挡土墙土压力计算时采用库仑土压力公式，库仑土压力公式假定墙后为砂性土，但工程中墙后填土常为黏性土，通常将黏性土的摩擦角转换为等效内摩擦角后计算土压力。为比较黏性土内摩擦角的变化对主动土压力以及挡土墙稳定的影响，在保持原始参数不变的基础上，分别改变模型中黏性土的摩擦角并将其转化为等效内摩擦角来表示土压力的变化规律。本文中选取黏性土摩擦角分别为10°、15°、20°，土体内聚力c=21kPa，计算所得等效内摩擦角分别是49°、56°、63°。计算仰斜式挡土墙土压力时的公式为：Ea=Ea'（1-tanα tanφ），在其他条件均不变的情况下，当φ增大至某一个值的时候，土压力将会出现负值，此时的计算结果不符合实际，应舍去。计算本文φ的临界值为68°，故计算时只计算至等效内摩擦角在68°以内的情况。改变土体内摩擦角值提交计算，提取各节点的土压力值绘制成图11。

图11 改变土体内摩擦角对各节点水平土压力的影响

提取模型中所求得的各单元的水平力并对其积分，得到墙背上的总水平土压力值，结果整理见表9。

表9 填土等效内摩擦角ϕd对水平土压力的影响

由表9可知，在等效内摩擦角逐渐增大的过程中，仰斜式挡土墙所受的土压力逐渐减小，利于挡土墙受力。在实际工程当中，采用摩擦角较大的土体可以尽量减少墙体受力，并可有效地减小挡土墙断面。

利用挡土墙安全系数计算公式，将各种内摩擦角所对应的安全系数计算并整理见表10和表11：

表10 填土内摩擦角ϕ对抗滑安全系数Ks的影响

表11 填土内摩擦角ϕ对抗倾覆安全系数Kt的影响

由表10和表11可以看出，当填土等效内摩角增大时，抗滑和抗倾覆安全系数是逐渐增大的。由于非黏性土的内摩擦角较大，产生的土压力较小，因此墙后填土尽量采用砂性土，可保证挡土墙的稳定性。当工程中不可避免地要使用黏性土时，可以在黏土中掺入粗砂或者提高压实质量。

3.3 基础埋深对挡土墙稳定性的影响

由于挡土墙基础嵌入的深度会影响墙前产生的土压力，通常认为，挡土墙的基础越深越利于墙体稳定，但墙体嵌入地基过深将增加施工难度，并且会大幅度地增加造价。为了保证工程的经济性，在满足稳定的前提下，尽量减少嵌入深度，故本文研究了地基深度对仰斜式挡土墙的稳定性的影响。

挡土墙的基础埋深应根据地形状况，地下水位、地基土类别、冻结深度等因素统筹考虑，通常取0.5～1m，当地基为基本岩层时，按表12选取。

表12 挡土墙基础埋置要求[2]

参考以上规定，改变本文中模型中的基础埋深，分别选取为0.6、1、2、3m，并提交计算，分析实际工程中基础埋深对挡土墙稳定的结果影响。当基础埋深为0.6m时，墙前产生塑性贯通区，即墙前已经发生挤出破坏，如图12所示：

故将变化范围调整为0.7、1、2、3m，分别提交计算，并将结果整理如下：

当基础埋深在增加的过程中，墙前的土压力会逐渐增大，因此我们关注墙前土压力有限元计算结果与理论计算结果的对比值，如表13所示：

图12 墙基深度0.6m时塑性变形云图

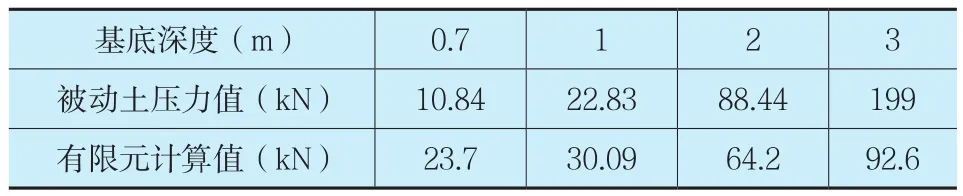
表13 墙前土压力有限元计算与理论计算值

由上述结果可以看出，当基础埋深大于2m时，墙前所产生的力小于被动土压力，在进行稳定计算时，应采取实际的土压力值进行计算，计算结果如表14、表15所示：

表14 基础埋深变化对挡土墙抗滑稳定系数的影响

表15 基础埋深的变化对挡土墙抗倾覆稳定系数的影响

由以上结果可以看出，随着基础埋深的增加，地基土体作用在墙体上的稳定力增大，抗滑安全系数逐渐增加；但由于基础埋深在增大的过程中，墙土墙基础和基础前、后土压力在对于墙趾点的抗倾覆力矩和倾覆力矩中所占的比例均在增大，当深度无限增大而墙体高度不变时，地表以上的墙体和土体所产生的抗倾覆力矩和倾覆力矩将远远小于基础墙体和基础前、后土压力所产生的力矩，此时的抗倾覆安全系数值接近于1，因此在基础埋深增加的过程中，抗倾覆安全系数略有减小，但仍然满足规范要求［3-6］。

4 结束语

本文利用ABAQUS有限元软件对仰斜式挡土墙进行了数值模拟分析，并对其计算结果进行分析；采用ABAQUS有限元方法，通过改变模型中各项参数，对影响仰斜式挡土墙稳定的关键因素进行数值分析，得到以下规律：随着墙后填土的弹性模量E、等效内摩擦角φd逐渐增大，墙后水平土压力逐渐减小，抗滑和抗倾覆安全系数呈逐渐增大的趋势；基础埋深逐渐增大时，墙体抗滑安全系数逐渐增大，抗倾覆安全系数略有降低，但仍然满足工程要求。

利用有限元模型可以真实的模拟工程实例并计算挡土墙稳定的相关参数，计算结果更接近工程实际情况，能够给设计和施工人员用于参考，指导设计。不足之处是本文只分析了填土弹性模量和内摩擦角变化对墙体应力和稳定的影响，并未考虑施工速度和不同断面形式对工程的影响，分析计算在不同断面形式以及不同施工速度下挡土墙的受力特性以及稳定性变化规律，为仰斜式挡土墙的设计提供更完整的资料。

[1]薛殿基，冯仲林.挡土墙设计实用手册[M].北京：中国建筑工业出版社.2008.

[2]顾慰慈.挡土墙土压力计算[M].北京：中国建材工业出版社.2001.

[3]庄茁.基于ABAQUS的有限元分析和应用[M].北京：清华大学出版社，2006.

[4]赵庆.土石坝坝下涵洞数三维有限元分析[D][硕士学位论文].郑州，郑州大学，2010.

[5]潘福营，李璟延.复杂地质条件下隧洞开挖支护施工技术［J］.水电与抽水蓄能.2015，1（2）：42～44.

[6]郭熔.响洪甸蓄能电站闸门槽混凝土贯穿性漏水处理施工技术应用分析[J].水电与抽水蓄能.2016，2（2）:50-55.

夏智翼（1986—），女，硕士，讲师，主要研究方向：水电站建筑物施工监测。E-mail:zhiyi-xia@sgxy.sgcc.com.cn

Influencing Factors Analysis of Retaining Wall Reclining on the Slight Slope

XIA Zhiyi
（Feng Man Training Center， State Grid Xin Yuan Company Ltd.Jilin 132108，China）

In many engineering，the safety of the retaining wall is closely related to the whole project.Because retaining wall reclining on the slight slope has good material properties， it is widely applied in the project.But now， the design instructions and examples for retaining wall reclining on the slight slope are less， and researches on the soil pressure of the retaining wall are not reasonable which could easily cause the problem in cracking and instability of retaining walls.In this paper， in view of above-mentioned problems; further research and discussion have been done on earth pressure， wall body stress，stability calculation， and other key issues of retaining wall reclining on the slight slope.

retaining wall reclining on the slight slope； soil pressure ； finite element method ； ABAQUS