沿石墨烯薄层传播的非线性表面等离激元

曹明，刘畅，孙坚，潘涛，徐国定

（苏州科技大学数理学院，江苏苏州215009）

沿石墨烯薄层传播的非线性表面等离激元

曹明，刘畅，孙坚，潘涛，徐国定*

（苏州科技大学数理学院，江苏苏州215009）

分析了沿石墨烯覆盖的各向异性Kerr非线性介质表面传播的非线性表面等离激元的性质。根据麦克斯韦方程组和边界条件并把石墨烯模拟为无限薄的表面电导率，导出了表面等离激元的色散关系。数值结果表明，当表面等离激元的传播常数小于某个临界值时，其色散曲线出现“双稳”态。改变石墨烯的化学势、光强或非线性系数可以有效地控制表面等离激元的色散和传播性质。

各向异性Kerr非线性介质；石墨烯；表面等离激元；色散关系

1902年，Wood[1]在光学实验中首次发现了表面等离激元共振现象。1941年，Fano等人[2]根据金属和空气界面上表面电磁波的激发解释了这一现象。Ritchie[3]注意到，当高能电子通过金属薄膜时，不仅在等离激元频率处有能量损失，在更低频率处也有能量损失，并认为这与金属薄膜的界面有关。1959年，Powell和Swan[4]通过实验证实了Ritchie的理论。1960年，Stren和Farrel[5]研究了此种模式产生共振的条件并首次提出了表面等离激元（Surface plasmon，SP）的概念。在以后的这几十年中，SP的研究如火如荼，并由此诞生了表面等离激元学（plasmonics）与亚波长光学，为新一代人工超材料提供了理论基础，并为SP全光器件及全光电路开辟了道路。

近年来，金属和介质界面上的SP的性质得到广泛研究[6-13]。SP的实质是金属表面电子在外加电磁场的激发下发生集体振荡所产生的电荷密度波，其振幅在垂直于表面的方向上随着传播深度的增加而成指数衰减，所以这是一种存在于金属与电介质界面附近的非辐射局域电磁场模式[14-15]。集成光路的全光信号处理要求用光来控制光，而非线性介质可以通过非线性系数和光强来调节其特性，这使得非线性的作用显得尤为重要。各种基于亚波长金属结构的非线性光学器件已经得到研究，此种新型器件在纳米尺度下可以得到明显的非线性效应，这是其他类型的器件无法比拟的[16-18]。

石墨烯（Graphene）是一种由碳原子构成的单层片状结构的新材料。它是一种由碳原子以sp2杂化轨道组成六角蜂巢型晶格的平面薄膜，只有一个碳原子厚度的二维材料。科学家们研究发现，石墨烯在一定条件下具有与贵金属类似的特性[19]。可以利用石墨烯的这种特性来代替金属来产生SP[20]。贵金属支持可见光至近红外波段的SP，且有较高的传播损失，而石墨烯可以支持太赫兹至中红外波段的SP[21-22]。另外，研究表明，在常温下石墨烯支持的SP具有较小的传播损失。更重要的是，通过外加栅极电压或掺杂的方法可以改变石墨烯的化学势，从而改变石墨烯的电导率分布情况，最终实现对SP传播特性的调控。

该研究讨论沿由石墨烯分离的各向异性Kerr非线性介质与线性介质的界面传播的SP的性质，如图1所示。从麦克斯韦方程组出发，结合边界条件，推导了TM波的非线性SP的色散关系，并讨论了石墨烯的化学势对SP的色散关系和传播长度的影响。

图1 石墨烯分离的线性介质与各向异性Kerr非线性介质的界面

1 理论描述

研究的模型如图1所示，z>0区域为各向异性Kerr非线性介质，z<0区域为各向同性、无吸收、非磁性的线性介质。

对于沿x方向传播的TM波，Ex，Ez，Hy各分量都含有因子ei（βx-ωt）。在z>0的区域，由麦克斯韦方程组得[23]

其中γ＝β/kr；ξ=krz；kr=ωr/c；ωr是磁共振频率；c是真空中的光速；μy是各向异性Kerr非线性介质的磁导率张量；εxx和εzz是各向异性Kerr非线性介质的电容率张量的，它们分别表示为[23]

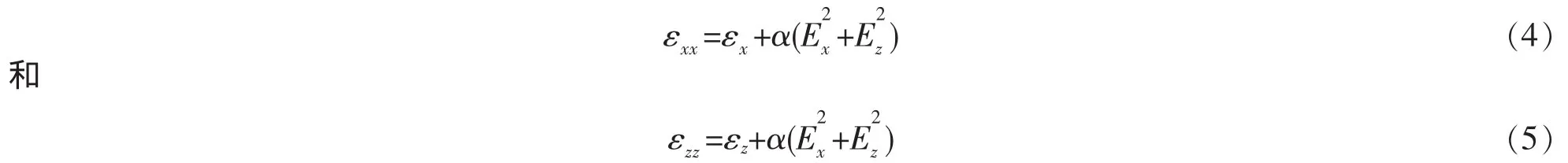
其中α是非线性系数；εx和εz是各向异性介质的线性部分电容率张量的对角元素，它们一般用与频率有关的Drude模型表示，分别是

同样的，有效磁导率μy可以表示为

在方程（6）和（7）中，不考虑损耗，约化频率Ω=ω/ωr，Ωpx=ωpx/ωr，Ωpz=ωpz/ωr，其中Ωpx和Ωpz是等离子体频率；F是介于0到1之间的常数。

从方程（1）和（2），可以得到

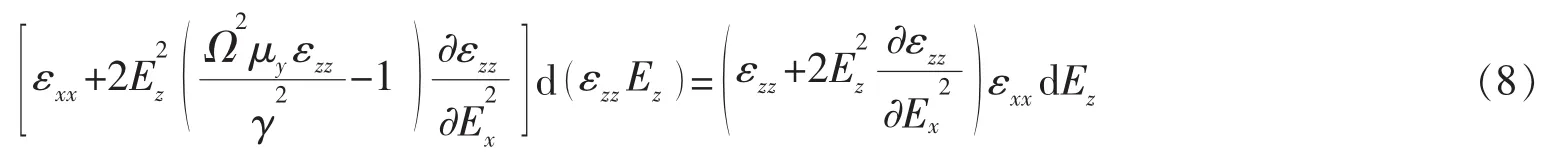
构造如下方程

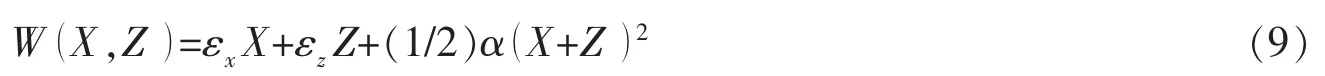
其中X=Ex2，Z=Ez2，可得

由方程（1）和（8）-（10）可得全微分

其中C是由边界条件决定的积分常数。

对于半无限非线性介质的SP，当ξ→∞（即z→∞）时，X和Z都趋向于0。积分常数C=W（0，0）=0。由方程

（9）和（12）可得

z<0的区域为线性介质，如果令εxx=εzz≡ε1且μy=1，则通过方程（1）-（3）可以得到

因为只有在这种情况下解才有物理意义。

在z=0处，由电场的切向分量的连续性（Ex1=Ex2）和磁场切向分量的边界条件（Hy1-Hy2=σEx）可得方程

其中Ex（0）和εzz（0）是在z=0+的界面处的值；σ是石墨烯的电导率，它包含带内电子跃迁和带间电子跃迁的贡献，当入射光子能量满足条件ħω<2μc时，带内跃迁占优势，此时σ为[24]

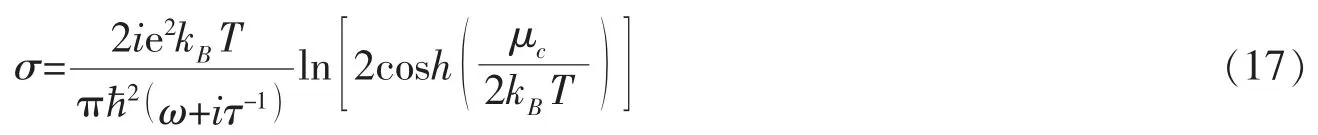
式中μc为石墨烯的化学势；e是电子电荷量；kB是玻尔兹曼常数；ħ是约化的普朗克常数；T是温度；τ是弛豫时间。

由方程（14）和（16）可以得到

其中Ex（0）是在z=0+的界面处的值，ρ＝1+qσ/Ωcε0ε1。对于TM波，E0=Ex2（0）+Ez2（0），结合式（18）有

在z=0处，结合方程（13）、（19）和（20），整理得到

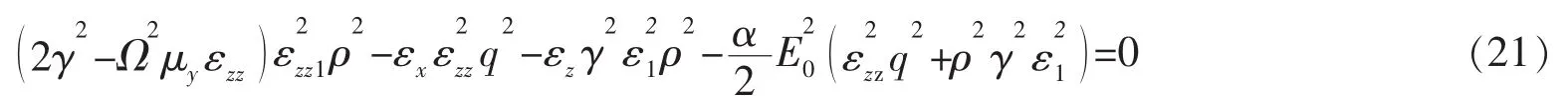
（21）式即为SP的色散关系，显然它与石墨烯的电导率有关，因此，改变电导率即可控制SP的传播性质。

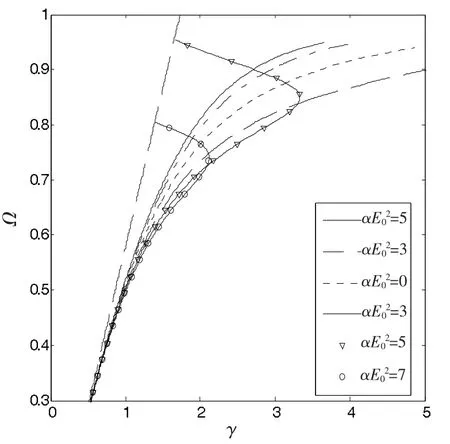
图2 不同的αE02对色散关系曲线的影响石墨烯的化学势μc=0.1 eV

2 数值结果和讨论

为了分析石墨烯对非线性SP传播特性的影响，必须进行数值计算。在计算中选择如下参数：T=300 K，F=0.56，ωr/2π=10 THz，Ωpx=2，Ωpz=2.5。

图2表示石墨烯的化学势μc=0.1 eV，不同的αE02值对SP色散关系的影响。其中最左边的直线为“光线”，即方程Ω=γ/ε1所对应的曲线。其他所有的色散曲线都在“光线”右边，这是由方程（15）所限制。在图2中，当αE02是负值或者比较小的正值时，色散曲线随着归一化传播常数单调递增。这表明SP的群速度是正的。但当αE02的值进一步增加时，大概大于5，色散曲线会有拐点，并

与“光线”有交点。在交点处，SP退化为线性各向同性介质中以速度传播的光子。而在拐点γt处，SP的群速度的符号发生了改变。显然，当γ>γt时，没有SP在表面传播，即γt是归一化截止波矢；而当γ<γt时，同一个波矢对应两个SPs，它们的群速度符号相反，共存于表面，即出现“双稳”态的SPs。而且随着αE02值的增加，拐点在下降，并且色散曲线在逐渐地靠近“光线”。从图中可见，当γ<0.5时，色散关系曲线与“光线”几乎重合，即αE02值对色散关系的影响不大。当γ>0.5时，色散曲线开始逐渐偏离“光线”，但各支曲线的偏离程度不一样，在αE02<0的情况下，αE02的绝对值越小，则色散曲线偏离程度越大，而在αE02>0的情况下，αE02的值越小，则色散曲线偏离程度越小。

如图3所示，由于石墨烯的化学势显示了在αE02=0时不同的石墨烯的化学势μc的值所对应的色散关系曲线。从图中可以看出，不管μc的值如何变化色散曲线都会有一个拐点γt，也就是说即使不考虑超颖材料非线性，即αE02=0，SP仍然有正负两个群速度。而且随着石墨烯化学势的增加，SP色散曲线的拐点γt不断向左边移动，即SP的传播常数的范围在逐渐变窄。在中高频率区域，化学势对色散特性影响较大，而在较低频率区域化学势对SP色散的影响减弱。因此，在中高频率区域可以通过改变石墨烯的化学势来控制SP的传播性质。

接下来讨论当超颖材料具有非线性时，石墨烯的化学势对SP性质的影响。图4显示了αE02=7时，不同的石墨烯的化学势μc的值所对应的色散关系曲线。由于非线性的存在，曲线呈现显著的“双稳”性质。当归一化频率Ω在区间[0.55，0.75]中时，各条色散曲线分离的空间不大，而在其它频率各条色散曲线几乎重合，可见在中频处，化学势对色散特性有影响，在低频和高频处化学势对SP色散的影响变得微弱。与图3比较得知，当非线性存在，石墨烯的化学势对表面等离激元的调控效果减小。

图3 不同的石墨烯化学势μc对色散曲线的影响参数αE02=0。最左侧的长虚线为“光线”

图4 在αE02=7时不同的石墨烯的化学势μc的值所对应的色散关系曲线最左侧的长虚线为“光线”

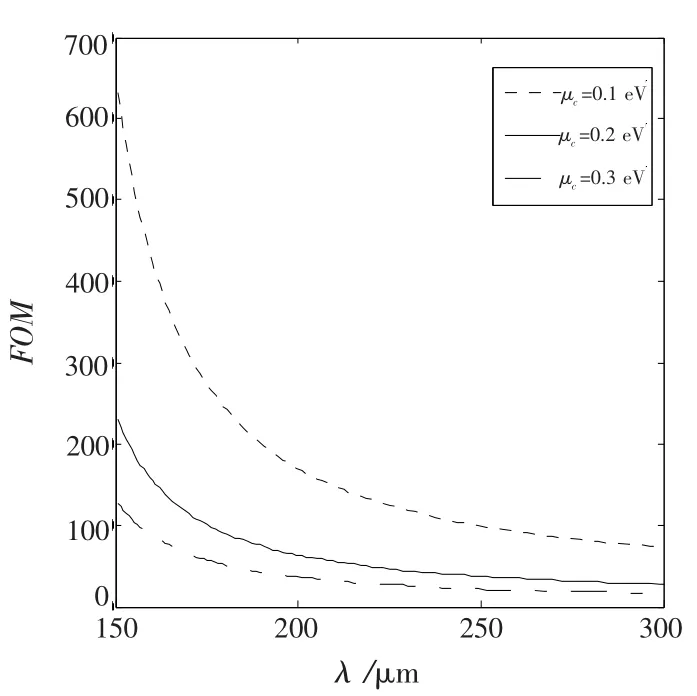
图5 不同μc的值时的品质因数（FOM）随波长的变化曲线

石墨烯的化学势μc不仅对SP的色散关系有影响，而且对其传播长度也有调控作用。图5中三条曲线显示了不同μc的值时的品质因数（figure-of-merit，FOM）。品质因数的表达式为

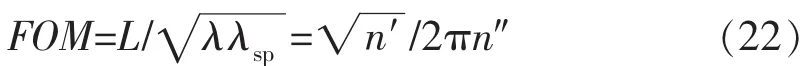
其中L为SP在表面的传播长度；λ是波长；λsp是等离激元波长；n′和n″分别是等离激元有效折射率的实部和虚部，它们满足如下表达式[25]

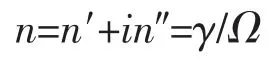
这个品质因数反映了由有效波长和自由空间波长的几何平均数归一化的传播长度。与直接探讨传播长度相比，由于对于不同的化学势和波长所对应的FOM区分更加明显。因此，可把FOM定义成该模型的特性参数。从图中显见，对于一定的化学势，随着横坐标Ω（即ω）的增加，传播长度单调减小。而从三条

曲线的比较来看，随着石墨烯的化学势μc的增加，传播长度在逐渐地减小，这意味着纯的石墨烯（无掺杂或无栅压过的石墨烯）更有利于长距离传播。因此，要通过石墨烯的化学势来调控研究系统的色散性质，就要以牺牲等离激元的传播长度为代价。为了兼顾传播长度，石墨烯的化学势的选择在0.5 eV以下。

3 结语

在各向异性Kerr非线性介质和线性介质的界面处引入了石墨烯薄层。通过麦克斯韦方程组和电磁边界条件，导出了SP的色散方程。由于有石墨烯的存在，色散关系不仅与非线性系数和光强的函数有关，还受到石墨烯的化学势μc的影响。通过数值计算，分析和讨论了这两个因素对SP的色散和传播特性的影响。结果发现，非线性的存在使色散曲线出现“双稳”性质，即同一个传播常数，对应两个频率不同、群速度符号相反的SPs。在中高频率范围，石墨烯的化学势对SP的色散特性有较为明显的调控作用。但在传播长度方面，增加化学势似乎不利于SP的传播。这些结果对于设计基于石墨烯结构的等离激元和光子器件有一定的借鉴意义。

[1]PORTO J A，GARCIA-VIDAL F J，PENDRY J B.Transmission resonances on metallic gratings with very narrow slits[J].Physical Review Letter 1999，83（14）：2845-2848.

[2]CAO Qing，LALANNE P.Negative role of surface plasmons in the transmission of metallic gratings with very narrow slits[J].Physical Review Letters，2002，88：057403.

[3]RITCHIE R H.Plasma losses by fast electrons in thin films[J].Physical Review，1957，106：874.

[4]POWELL C J，SWAN J B.Origin of the characteristic electron energy losses in aluminum[J].Physical Review，1959，115：869-871.

[5]STERN E A，FERRELL R A.Surface plasma oscillations of a degenerate electron gas[J].Physical Review，1960，120：130.

[6]BARNES W L，DEREUX A，EBBESEN T W.Surface plasmon subwavelength optics[J].Nature，2003，424：824-830.

[7]SMOLYANINOVII.Quantum fluctuations of the refractive index near the interface between a metal and a nonlinear dielectric[J].Physical Review Letters，2005，94：057403.

[8]SHIHaofei，WANG Changtao，DU Chunlei，et al.Beam manipulating by metallic nano-slits with variant widths[J].Optics Express，2005，13：6815-6820.

[9]YANG Pengfei，GU Ying，GONG Qihuang.Surface plasmon polariton and mode transformation in a nanoscale lossy metallic cylindrical cable[J].Chinese Physics B，2008，17：3880.

[10]ZHOU Renlong，CHEN Xiaoshuang，ZENG Yong，et al.Enhanced transmission through metal-film hole arrays and the surface plasmon resonance[J].Acta Physica Sinica，2008，57：3506-3513.

[11]ZHANG Haixi，GU Ying，GONG Qihuang.A visible-near infrared tunable waveguide based on plasmonic gold nanoshell[J].Chinese Physics B，2008，17：2567.

[12]SUN Mei，LIU Rongjuan，LIZhiyuan.The influence of hole shape on enhancing transmission through subwavelength hole arrays[J].Chinese Physics，2006，15：1591.

[13]MENG Kuo，WANG Yanhua，CHEN Longwang，et al.Resonant transmission of the terahertz pulse through a subwavelength metallic slit[J].Acta Physica Sinica，2008，57：3198-3202.

[14]BARNES W L，DEREUX A，EBBESEN T W.Surface plasmon subwavelength optics[J].Nature，2003，424（6950）：424824-424830.

[15]VASA P，WANG Wei，POMRAENKE R，et al.Real-time observation of ultrafast Rabi oscillations between excitons and plasmons in metal nanostru[J].Nat Photon，2013，7：128-132.

[16]WURTZ G A，ZAYATS A V.Nonlinear surface plasmon polaritonic crystals[J].Laser＆Photon Review，2008，3：125-135.

[17]MIN Changjun，WANG Pei，JIAO Xiaojin.Optical bistability in subwavelength metallic grating coated by nonlinear materialter[J].Optics Express，2007，15：12368-12373.

[18]PORTO J A，MARTIN M L，GARCIA V F J.Optical bistability in subwavelength slit apertures containing nonlinear media[J].Physical Review B，2004，70：081402.

[19]JABLAN M，BULJAN H.Plasmonics in graphene at infrared frequencies[J].Physical Review B，2009，80：245435.

[20]KOPPENS F H L，CHANF D E，ABAJO F J G.Graphene plasmonics：A platform for strong light-matter interactions[J].Nano Letters，2011，8：3370-3377.

[21]LIZ Q，HENRIKSEN E A，JIANG Z，et al.Dirac charge dynamics in graphene by infrared spectroscopy[J].Nature Physics，2008，4：532-535.

[22]JABLAN M，BULJAN H，SOLJAM.Plasmonics in graphene at infrared frequencies[J].Physical Review B，2009，80：245435.

[23]XU Guoding，PAN Tao，ZANG Taocheng，et al.Nonlinear surface polaritons in anisotropic Kerr-type metamaterials[J].Journal of Physics D：Applied Physics，2009，42（4）：45303-45309.

[24]FALKOVSKY L A.Optical properties of graphene[J].Journal of Experimental&Theoretical Physics，2008，115（3）：496-508.

[25]GAN C H，CHU H S，LIE P.Synthesis of highly confined surface plasmon modes with doped graphene sheets in the midinfrared and terahertz frequencies[J].Physical Review B Condensed Matter，2012，85（12）：117-122.

Nonlinear surface plasmons propagating along graphene sheets

CAO Ming，LIU Chang，SUN Jian，PAN Tao，XU Guoding
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

In this paper,we analyzed the nonlinear surface plasmons（SPs）propagating along the graphene sheets sandwiched between an anisotropic Kerr-type nonlinear medium and a linear isotropic medium.Following Maxwell's equations and the boundary conditions and modeling graphene as an infinitesimally thin surface conductivity,we derived the dispersion of the nonlinear SPs.The numerical results indicate that the dispersion of the SPs exhibits bistability when the propagation constants are smaller than their critical values.The dispersion and propagation properties of the SPs can be effectively controlled by changing the chemical potential of the graphene,the optical intensity or the nonlinear coefficient.

anisotropic Kerr-type nonlinear media；grapheme；surface plasmon；dispersion

O441.4

A

1672－0687（2016）04－0028－06

责任编辑：李文杰

2015－06－16

江苏省高校自然科学基金资助项目（13KJB140017）

曹明（1988-），男，江苏常州人，硕士研究生，研究方向：光学微结构与电磁波传播。

*通信联系人：徐国定（1965-），男，教授，博士，E-mail：guodingxu@163.com。