集值映射的单值广义模糊积分

马朝晖，吴健荣

（苏州科技大学数理学院，江苏苏州215009）

集值映射的单值广义模糊积分

马朝晖，吴健荣*

（苏州科技大学数理学院，江苏苏州215009）

借助于广义三角模给出了集值可测映射一种新的模糊积分的定义，它是单值可测函数的模糊积分的推广。在给出该积分的一些基本性质的基础上，得到了该积分的一个重要收敛定理。

可测集值映射；模糊测度；广义三角模；模糊积分

1 预备知识

对集值积分的系统研究可以追溯到20世纪60年代。1965年，Aumann[1]以可测集值函数的单值Lebesgue可积选择定义了Rn空间中集值函数的积分，并讨论了该积分的一些基本性质。伴随着模糊测度和模糊积分[2]的发展，1990年，王子孝，张德利[3]针对一些特殊的模糊测度，如λ-测度，讨论了集值模糊积分。此后，文献[4－5]采用Aumman积分的定义方式，分别将集值函数的取值限制在[0，1]和R+的幂集上，利用单值可测选择的模糊积分定义了集值函数的模糊积分，自然，这些积分的取值均为集合。

关于集值映射单值模糊积分的研究也取得了一定进展。2001年，文献[6]将集值函数的取值限制在[0，1]的幂集上，类似Sugeno积分给出了集值映射模糊积分的定义，并研究了该积分的一些基本性质及Fatou引理和Lebesgue收敛定理。2012年，Croitoru在文献[7]中给出了取值为实线性空间幂集的集值函数的单值模糊积分定义，证明了该积分的单调收敛定理和一致收敛定理。2014年，文献[8]则研究了取值为R+的子集的集值映射及其模糊积分。

笔者通过引入了广义三角模，给出了集值映射单值广义模糊积分的定义，并研究该积分的一些基本性质。引进的概念和所得到的结论是已有相应概念和结论的推广。

文中，Ω总表示一非空集合，∑为Ω上的一个σ-代数，从而（Ω，∑）为可测空间。R+＝[0，∞），P0（R+）表示R+的全体非空子集。对于集值映射F：Ω→P0（R+），记

定义1[2]若集函数μ：∑→[0，+∞]满足以下条件：

（1）μ（Φ）=0；

（2）A，B∈∑且A⊂B则μ（A）≤μ（B）（单调性）；

（3）A1⊃A2⊃…⊃An⊃…，An∈∑，∀n∈N，并且存在n0∈N，使得μ（An0）＜+∞，则；

（4）A1⊂A2⊂…⊂An⊂…，An∈∑，∀n∈N，则；

则称μ为模糊测度，相应的（Ω，∑，μ）称为模糊测度空间。其中（3）、（4）分别称为上、下连续性。

定义2[2]称集函数μ：∑→[0，+∞]

（1）是次可加的，若∀A，B∈∑，有μ（A∪B）≤μ（A）+μ（B）；

（2）是零可加的（零可减的），若∀A，B∈∑，μ（B）=0，有μ（A∪B）=μ（A）（μ（A-B）＝μ（A））。

定义3[9]记D＝[0，+∞]2/{（0，+∞），（+∞，0）}，映射S：D→[0，+∞]称为是广义三角模，若其满足条件：

（1）S[x，0]=0，∀x∈[0，+∞），且存在e∈（0，+∞]，使得S[x，e]=x，∀x∈（0，+∞]，这里e称为单位元；

（2）S[x，y]=S[y，x]；

（3）当x1≤x2，y1≤y2时S[x1，y1]≤S[y2，x2]；

（4）若{（xn，yn）}⊂D，（x，y）∈D且xn↑x，yn↓y则S[xn，yn]→S[x，y]。

注1S[x，y]=min（x，y），S[x，y]=kxy（k＞0）均为广义三角模，其中S[x，y]=min（x，y）的单位元为∞，S[x，y]= kxy的单位元为1/k。

定义4[10]称广义三角模S是次可加的，若∀x，y∈[0，+∞]，有

定义5[9]设（Ω，∑，μ）为模糊测度空间，S是广义三角模，f是非负可测函数，则f在A上的广义模糊积分为

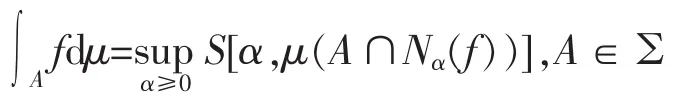
其中Nα（f）={ω|f（ω）＞α}。

定义6[11]称集值映射F：Ω→P0（R+）可测，若F-1（U）∈∑，（∀闭集U⊆R+）。

定义7[8]设（Ω，∑，μ）为模糊测度空间，集值映射F：Ω→P0（R+）是可测的，A∈∑，则F在A上关于μ的积分定义为

方便起见，以下记F-1（[α，+∞））=Fα，∀α∈[0，+∞）。

2 主要研究

首先，利用广义三角模，给出集值映射一种新的模糊积分定义。

定义8设（Ω，∑，μ）为模糊测度空间，F：Ω→P0（R+）是可测的集值映射，A∈∑，F在A上的单值广义模糊积分（简称为（G）积分）定义为

注2若F为单值函数时，可看出该定义是定义5单值可测函数模糊积分的推广；若S[x，y]=min（x，y），则该积分定义即为定义7。

下面讨论该积分的若干性质，首先从定义8可以直接得到以下结论：

定理1设（Ω，∑，μ）为模糊测度空间，F：Ω→P0（R+）是可测的集值映射，A∈∑。

（3）若F（ω）={a}，∀ω∈Ω，a∈（0，+∞），则（G）。

（5）F1，F2：Ω→P0（R+）是可测的集值映射，且∀ω∈Ω，F1（ω）⊂F2（ω），则。

（7）设μ，S次可加，F，G：Ω→P0（R+）是可测集值映射，则。

定理2设（Ω，∑，μ）为模糊测度空间，F：Ω→P0（R+）是可测集值映射，B∈∑，μ（B）=0。

证明（1）由μ的单调性及μ（B）=0可得μ（B∩Fα）=0。又μ是零可加的，则

（2）的证明类似。

定理3设（Ω，∑，μ）为模糊测度空间，μ是零可加的当且仅当对于可测集值映射F，G：Ω→P0（R+），F＝G μ-a.e蕴含。

证明必要性：设μ是零可加的，F，G：Ω→P0（R+）是可测的集值映射且F＝G μ-a.e。令A={ω∈Ω|F（ω）≠G（ω）}，则有μ（A）=0。由μ的单调性，对任意α∈[0，+∞），有μ（Fα）≤μ（Gα∪A）。再由μ是零可加的及μ（A）=0，可知μ（Gα）=μ（Gα∪A），所以μ（Fα）≤μ（Gα）。类似可得μ（Gα）≤μ（Fα）。

所以对任意α∈[0，+∞），有μ（Fα）=μ（Gα），进而由定义8可得。

充分性：设A，B∈∑，μ（B）=0，要证μ（A∪B）=μ（A），下面分两种情况讨论：

（1）当μ（A）=+∞时，由μ的单调性可得μ（A∪B）=+∞=μ（A）。

（2）当μ（A）＜+∞时，定义可测集值映射F，G：Ω→P0（R+）如下：∀ω∈Ω，

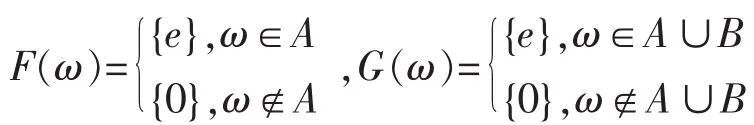
其中e是S的单位元。则{ω∈Ω|F（ω）≠G（ω）}=B-A，由μ的单调性可得

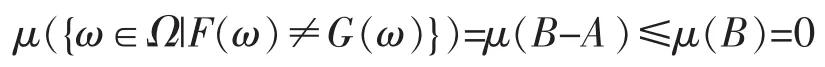
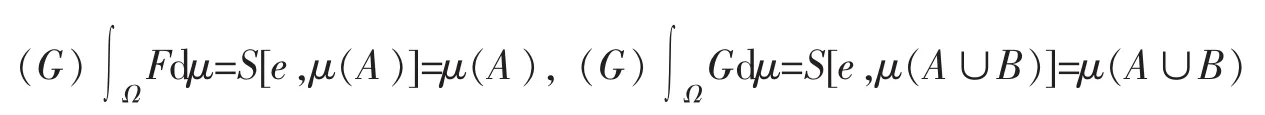
所以μ（A）=μ（A∪B），即μ是零可加的。

推论1若μ零可加，F=G在A上μ-a.e（∀A∈∑），则。

证明充分性：由于对任意α∈[0，+∞）有S[α，μ（Fα）]≤β，所以。另外，由于

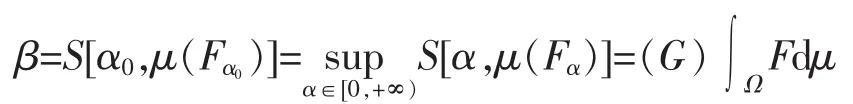
（1）若αnk↑∞，则μ（Fαnk

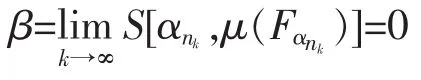
与β∈（0，+∞）矛盾。

（2）若αnk↓0，则由μ（Ω）＜+∞知

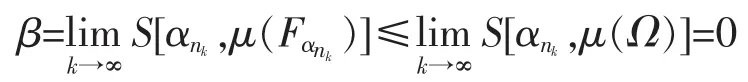
与β∈（0，+∞）矛盾。

（3）若αnk单调收敛于α0∈（0，+∞），则单调收敛于，由广义三角模的性质有

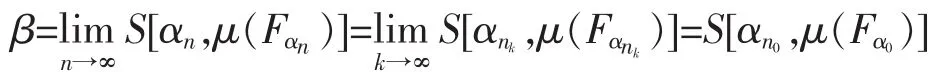
即存在α0∈（0，+∞），使得S[αn0，μ（Fα0）]=β。证毕。

最后，给出文中定义的积分的一个重要收敛定理。

定理5设（Ω，∑，μ）为模糊测度空间，Fn：Ω→P0（R+）是可测集值映射列，且Fn（ω）⊂Fn+1（ω）（∀ω∈Ω，n∈N），定义

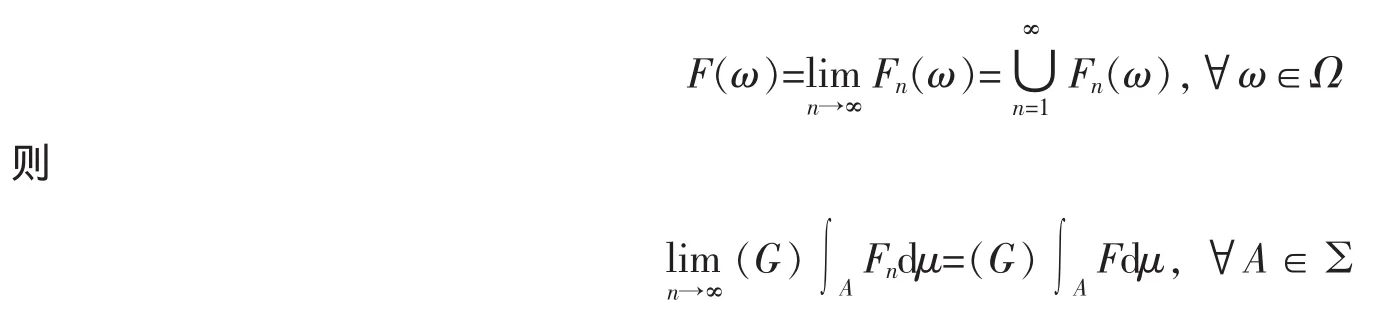
证明由文献[11]中的命题3.4知，F是可测集值映射。不失一般性，设A＝Ω（对∀A∈∑，类似可证）。因为Fn（ω）⊂Fn+1（ω）⊂F（ω）（∀ω∈Ω，n∈N），所以由其积分性质有

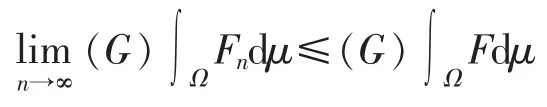
性知

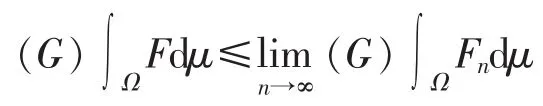
（3）当I＝+∞时，则有αk使得S[αk，μ（Fαk）]＞k（k＝1，2，…），类似（2）的证明知存在nk，使得当n≥nk时S[αnk，μ（（Fn）αnk）]＞k，所以

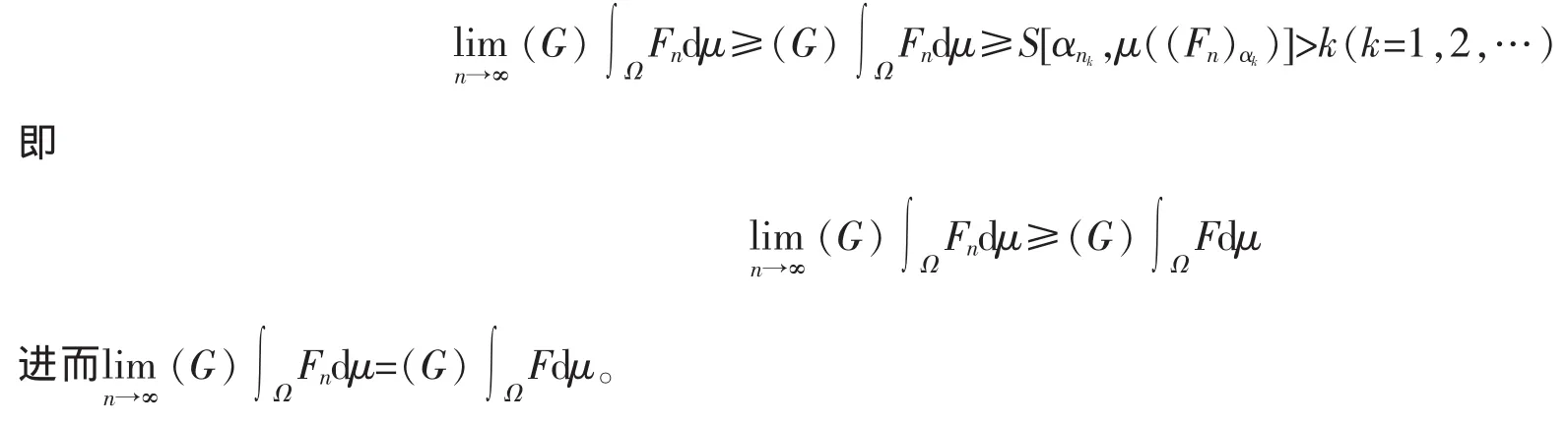
[1]AUMANN J.Integrals of set－valued functions[J].J Math Anal Appl，1965，12：1-12.

[2]SUGENO M.Theory of fuzzy integrals and its applications[D].Tokyo：TokyoInstitute of Technology，1974.

[3]王子孝，张德利.集值函数的模糊积分[C]//中国模糊数学与模糊系统学会第五届年会论文集.成都：西南交通大学出版社，1990：102-105.

[4]ZHANG D，GUO C.Fuzzy integrals of set-valued mappings and fuzzy mappings[J].Fuzzy Sets and Systems，1995，75（1）：103-109.

[5]ZHANG D，GUO C.Generalized fuzzy integrals of set－valued functions[J].Fuzzy Sets and Systems，1995，76（3）：365-373.

[6]CHO S J，LEE B S，LEEG M，et al.Fuzzy integrals for set－valued mappings[J].Fuzzy Sets and Systems，2001，117（3）：333-337.

[7]CROITORU A.Fuzzy integral of measurable multifunctions[J].Iran J Fuzzy Systems，2012，9（4）：133-140.

[8]CROITORU A.Strong integral of multifunctions relative to a fuzzy measure[J].Fuzzy Sets and Systems，2014，244（1）：20-33.

[9]WU C X，WANG S L，SONG S J.Generalized triangle norms and generalized fuzzy integrals[C]//Proc of Sino-Japan Sympo on Fuzzy Sets and Systems.Beijing：International Academic Press，1990.

[10]夏阳，吴健荣.一般可测函数的（G）模糊积分[J].模糊系统与数学，2011，25（1）：96-102.

[11]CASTAING C，VALADIER M.Convex Analysis and Measurable Multifunctions[M].Berlin Heidelberg，New York：Springer，1977.

Single-valued generalized fuzzy integrals of set-valued mappings

MA Zhaohui，WU Jianrong
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

By using the generalized triangle norm,we introduced a new concept of a fuzzy integral of a measurable set-valued mapping,which generalized the fuzzy integral of a measurable single-valued function.After presenting some basic properties of this integral,we obtained an important convergence theorem of it.

measurable set-valued mappings；fuzzy measure；generalized triangle norm；fuzzy integral

O159MR（2000）Subject Classification：28B20

A

1672－0687（2016）04－0023－05

责任编辑：谢金春

2014－10－28

国家自然科学基金资助项目（11371013）

马朝晖（1990-），女，河南周口人，硕士研究生，研究方向：非线性分析。

*通信联系人：吴健荣（1963-），男，教授，博士，硕士生导师，E-mail：jrwu@mail.usts.edu.cn。