基于熵权的集对分析方法在水质评价中的应用——以郑州市为例

陈 隽， 洪思扬， 程 涛， 焦志倩

(1.环境保护部 华南环境科学研究所,广东 广州 510655；2.北京师范大学 水科学研究院，北京 100875)



基于熵权的集对分析方法在水质评价中的应用
——以郑州市为例

陈 隽1， 洪思扬2， 程 涛2， 焦志倩2

(1.环境保护部 华南环境科学研究所,广东 广州 510655；2.北京师范大学 水科学研究院，北京 100875)

采用基于熵值的集对分析评价方法对郑州市伊洛河七里铺和黄河花园口两个地表水监测点的水质进行分析，计算出这两个监测断面的水质评价结果，并进一步将计算结果与其它两种水质评价方法的结果进行了对照.结果表明，在水质分析中，基于熵权的集对分析法与其他评价方法的结果较为吻合，且能更好地反映水质状况.该方法基于VBA编程，易于操作，可以为水环境保护与管理决策提供技术支持.

水质评价；熵权；集对分析；VBA

水污染一直是困扰着人类的一个重大环境问题，每年我国由于水质污染造成的人员伤亡、经济损失不可估量.近三十年来，由于经济的飞速发展，污水排放量增大，大量工业垃圾、农业污染物没有得到充分处理即被排放，造成了江河湖泊水质的严重污染，且水体污染有加重趋势，了解水质污染的具体情况，是有效控制和治理水污染.实施合理高效的水资源管理的基础.水质评价是了解水体情况的重要一步，对水质监测结果进行分析评价，对保护和治理水环境，推动水环境管理与社会经济发展的高效融合，具有重要的现实意义.

目前，水质评价的方法较多.其中，单因子评价法是在各个水质单项评价指标中，选取最差的一项作为评价最终水质级别的依据，这是现行国家水质标准中已经确定的悲观评价原则，对相关管理部门的监察有重要意义，但无法对水质做出综合评价.污染指数评价法是将各个水质单项评价结果与评价标准相除，得到该项评价指标的分指数，继而通过相关数学方法的运用，计算得到水质的综合污染指数.但该方法也存在一定弊端，如水质评价结果是相对值，无法得到明确的水质分类级别.模糊综合评价法是针对水质评价指标、各个水质级别的分类标准具有模糊性这一特点而发展的一种应用较为广泛的方法，其弊端在于评价结果的表达形式是隶属度矩阵，呈现形式并不直观.灰色系统分析法是将整个水体看作一个拥有部分已知信息和部分不确定信息的灰色系统，通过计算各项评价指标的实测值与对应指标评价标准的关联度，进而确定评价水体的水质级别，但该方法较为复杂，不太易于计算.每种评价方法都有其优缺点[1-4].水质状况本身即具有不确定性，评价指标与分类等级之间存在一定的非线性关系[5].因此，恰当的评价方法的选取在水质分析中具有重要作用.

集对分析(Set pair analysis，简称SPA) 是我国民间学者赵克勤结合确定性分析和不确定性分析方法，于1989年首次提出的一种利用联系度描述和处理综合集成问题的一种全新的系统分析方法，该方法已广泛应用于水质评价工作中.集对分析可用于处理模糊、随机和信息不完全所致的不确定性系统的理论和方法[6]，利于水质因子与水质等级间复杂的非线性关系的反映.因此，将该分析应用于水环境质量评价是合理且可行的.本文将集对分析方法引入伊洛河的水质评价中，并将研究结果与传统方法进行对照，以验证其合理性，进而为区域水环境保护与管理决策提供技术支持.

1 基于熵权的水质集对分析模型构建

1.1 集对分析基本模型的构建

(1)集对分析理论的基本原理 设X和Y是有联系的两个集合，X集合中有n个对象，即X=(x1,x2,…,xn)，Y集合中亦有n个对象，即Y=(y1,y2,…,yn).集合X与集合Y构成集对H(X,Y)，其联系度可以定义为

(1)

式中：μx-y表示集合X和Y的联系度；S为集对H(X,Y)中具有同一性的对象的数目；F为具有差异性的对象的数目；P为具有对立性的对象的数目；三者之和为n.代表差异度系数，取值范围在-1～1之间，当其取值为1时，差异性即转化成同一性；其值越趋于0，即表现越显著的不确定性.j代表对立度系数，这里将其取值为-1.若令a=S/N为同一度，b=F/N为差异度，c=P/N为对立度，则(1)式可改写为

(2)

a越趋近于1，表明集合X和Y的特征越趋近于同一；c越趋近于1，表明集合X和Y的特征越趋近于对立；b越趋近于1，表明集合X和Y的特征越趋近于差异.

在水质评价中，将水质监测数据作为集合X，将监测项目所对应的水质等级划分指标作为集合Y，使实际监测的评价因子数据与水质评价标准指标间构成一个集对，通过计算2个集合的联系度，评判水质级别.

(2)确定联系度 在不确定系统中，联系度可以对具有一定关联的两个集合进行量化，从而清晰地显示两者之间的定量关系.首先按单因子评价方法，参照《国家地表水环境质量标准》，计算出每个单项指标的水质等级.对于处于某个等级内的单项指标，我们定义其与该等级的联系度为1，定义其与该单项的水质等级相隔的水质等级的联系度为-1，对于相邻的水质等级，则通过联系度来确定实测指标与评价指标之间的距离，计算公式如下.

a. 样本i的第j项实测指标与第Ⅰ级水质联系度表示如下：

(3)

式中:xij为样本i第j项的实测指标值；s1j，s2j为指标分类的限制值.

b. 样本i的第j项实测指标与第Ⅱ级水质联系度表示如下：

(4)

式中:s3j为指标分类的限制值.

c. 样本i的第j项实测指标与第Ⅲ级水质联系度表示如下：

(5)

式中:s4j为指标分类的限制值.

d. 样本i的第j项实测指标与第Ⅳ级水质联系度表示如下：

(6)

式中:s5j为指标分类的限制值.

e. 样本i的第j项实测指标与第Ⅴ级水质联系度表示如下：

(7)

式中：s5j为指标分类的限制值，为了便于计算评价指标位于Ⅴ级时与Ⅳ级评价标准之间的联系度，将s5j赋值为2s4j-s3j.

1.2 熵值法确定权重

权重是针对某一研究对象而言的相对指标，同其他研究方法相比，熵值法能够更加有效地反映指标信息熵值的效应，较适应于水质污染情况的评价[7].熵权的大小与被评价对象的指标值有显著的联系，根据其原理，标准化方法的选择和实测指标数据的性质是影响赋权的重要因素[8].在水质评价的权重确定中，引入熵值这一概念来反映水质指标值的无序化程度，利用信息熵这种方法，根据各个评价指标之间的差异度，进而计算出各个评价指标的权重.相对于其它赋权方法，熵值法是相对渐变且有效的[9].具体计算步骤如下.

(1)数据标准化 设有m个采样点、n项指标，用原始数据矩阵X=(xij)m×n(i=1,2,…,m;j=1,2,…,n)表示.这里采用极值处理法对原始数据进行标准化，转换公式如下：

(8)

(9)

(2)熵值法的原理 传统熵值法定义各个评价指标的熵：

(10)

从(10)式中可以看出，若fij=0，lnfij是没有意义的，故需要对fij进行修正，进一步将其定义为

(11)

计算评价指标的熵值为W，W=(Wj)1×n.

(12)

通过上面的公式可以计算出各特征权重系数.

(3)联系度的确定 样本与各评价等级之间的联系度，并加权处理：

(13)

式中：μik为样值i与评价等级k之间的联系度；μijk为样本i中评价等级j对k评价标准的联系度，选取联系度数值最大的评价等级作为最终水质的评价等级.

1.3 基于熵权的集对分析方法在VBA编程中的实现

Visual Basic for Applications简称VBA，是一种编程语言，是微软公司开发出的，用以完成通用的自动化任务.主要能用来扩展Windows的应用程式功能，特别是Microsoft Office软件.基于Excel的VBA编程功能，对录入到Excel中的数据进行批量化处理，通过中间程序的功能实现，直接在表格中给出每个样本的水质等级，具体计算步骤如下.

首先按固定的格式录入水质数据和水质标准，录入的水质数据和水质标准分别放在两个Excel工作表(“水质数据”及“水质标准及熵值”)中，以便分别调用.数据录入应该按照固定的格式，便于程序的运行管理.

第二步是计算熵权值，即对所有样本按前文所述步骤计算每个水质指标的熵权值(占最终水质等级的比重)，熵权值的计算与所给的样本值的多少有关，样本值越多，越能反应区域变化特征和时间变化特征.熵权值计算在VBA中的实现需要借助多层循环语句和选择语句，以便于精简程序语言，减少运行时间.计算出的熵权值存储在一个“水质标准及熵值”工作表中水质标准之后.

第三步是计算分级联系度，即利用水质数据和水质标准，应用前文所述原理和公式，进行编程语言的设计，批量计算出每个水质指标与每个水质等级的联系度，并放入“单项联系度”工作表中.然后根据第二步计算得到的每个水质指标的熵权值，乘以相应的水质指标的联系度.最后，对水质指标中与相同水质等级的联系度相加，得到水质样本与五个水质等级的最终联系度，放入“最终联系度”工作表中.

最后，对于每个水质样本，分别确定联系度最大的那个水质等级，作为水质样本的水质等级，放入“水质数据”工作表中相应的水质样本后.

2 实例应用

伊洛河流域地处我国黄河流域的中段，位于东经109°45′-113°06′、北纬33°33′-35°05′之间，流域面积18881km2，属暖温带季风气候区，春季干燥多风，夏季易发暴雨，秋冬干旱少雨，多年平均径流量为27亿m3.流域地势险峻，地形复杂多样.流域中部及西部地区降水量大，洛河和伊河两岸的丘陵区降水量较少，降水量随海拔高度增加而减少，是黄河中部的重要供水来源之一.

为了验证集对分析方法的合理性，本文采用郑州市的伊洛河七里铺和黄河花园口两个地表水监测断面2010、2011和2012年各月的水质监测数据，以溶解氧(DO)、高锰酸盐指数(M)、五日生化需氧量(BOD5)、氨氮 (NH4-N)、化学需氧量(COD)、总氮(N_total)、总磷(P_total)、粪大肠菌群(Coo_org)为评价指标，分类标准参照《地表水环境质量标准》(GB 3838-2002)，详见表1.

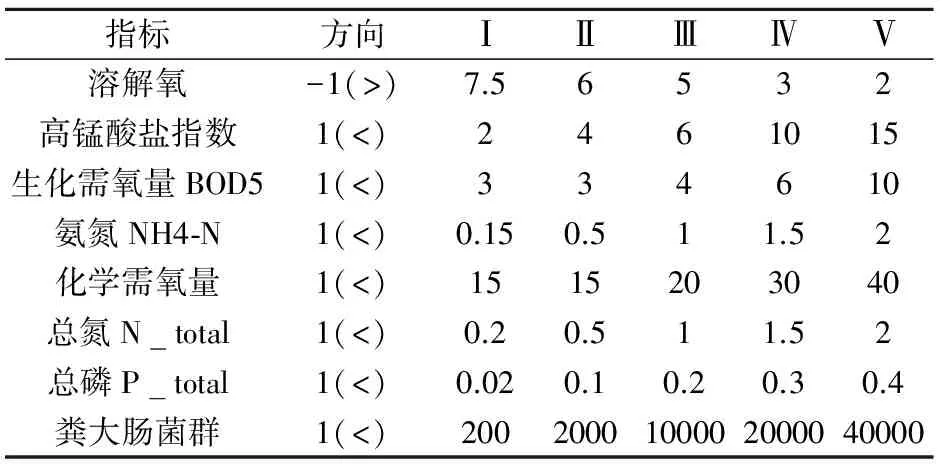
表1 地表水环境质量标准

这里以伊洛河七里铺监测断面的实测水质数据为例，对基于熵权的集对分析方法在水质评价中的应用进行具体说明.表2为七里铺断面2010年1月的水质指标值.首先，根据熵权值计算公式，得出各指标在水质评价中的权重分别0.123,0.131,0.149,0.118,0.111,0.116,0.139和0.113.其次，计算得到水质指标与五个等级的联系度，结果如表3所示.从表中最后一行可以看出，该测量断面在该日的水质等级为Ⅳ类.参照此方法，计算七里铺和花园口2010、2011、2012年各月的水质等级，结果见表4.

表2 七里铺断面水质指标值

3 结果讨论与分析

从表4中可以看出单因子分析的计算结果普遍高于集对分析和模糊数学综合分析法的计算结果，这是因为单因子分析法是将各项水质评价指标中最大的一项作为最终的数值等级，故指标相对偏高，也是不太能够反映实际情况的；同时，集对分析与模糊数学综合分析方法对水质的评价结果在大部分的月份保持一致，这是由于两种方法都是基于较为复杂的数学方法进行评价，两种结果能够互相验证，一定程度上验证了集对分析方法的有效性.

表3 水质指标与五个等级的联系度

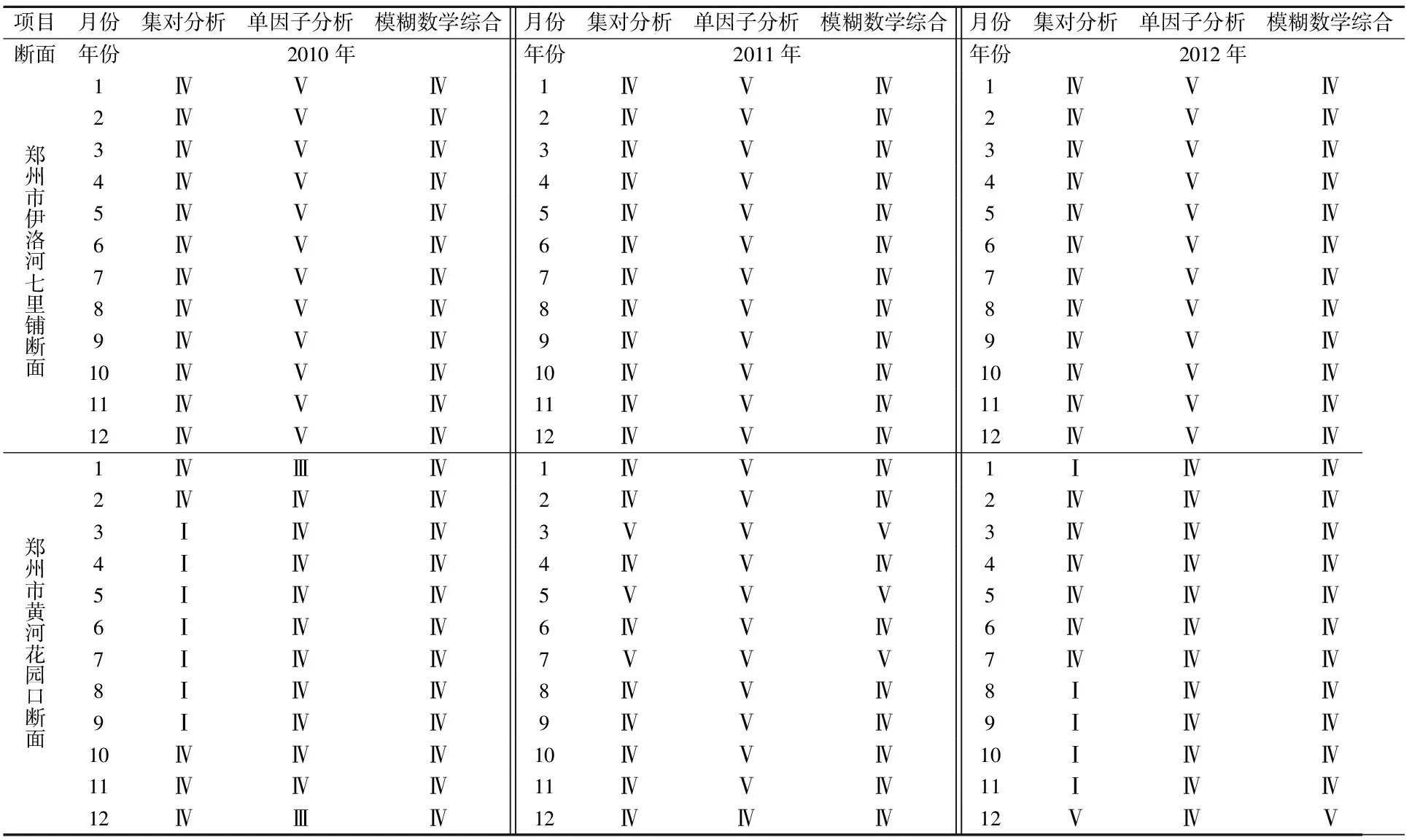
表4 郑州市某监测断面不同时间的水质监测结果等级

但是在花园口断面若干月份的评价结果中，集对分析与模糊数学综合分析方法得出的结果差异较大，这是因为模糊综合评价过程中，较常采用是线性加权平均法，评价结果容易出现失真的现象，且计算过程比较复杂，实际操作性较差[10].集对分析方法能综合反映水质不同指标的特征，较好地体现水质的实际情况.

同时，我们发现，在花园口断面若干个监测月份的评价结果中，集对分析的结果明显小于单因子分析和模糊数学综合分析的评价结果，可能的原因包括两方面：一是两种评价方法本身存在差异.两种评价方法都是基于相应函数的建立，模糊综合评价的水质等级是通过隶属度的值确定的，其取值范围在0-1之间，但不同水质等级之间如何过渡没有给出描述，而集对分析法的水质等级是通过联系度而确定的，其取值范围在-1-1之间，且不同水质等级之间的过渡性通过差异度、对立度等指标表现，因而评价结果更为准确、合理.二是两种评价方法的权重是通过不同方法确定的.对于模糊综合评价而言，其权重是由水质的实测值与对应的评价指标相除获得的，使得权重只与水质的实测值相关，进而导致某一类实测值偏高使得整体评价结果偏高现象的发生，从而使其评价结果高于集对分析法的评价结果.此外，模糊综合评价法是根据单一数值确定权重的方法，本身存在一定的误差.本研究在计算权重时运用信息熵的方法，这样能够减小单一指标确定权重时所产生的误差，并且能够体现各个评价指标的集中趋势.

另外，花园口站位于七里铺站的下游，伊洛河作为黄河中游的主要支流，对于黄河的水质会产生较大的影响.通过这两个监测断面数据的评价结果可知，单因子评价法及模糊数学综合评价法的评价结果表明，花园口断面的水质相较于七里铺断面更好，而利用集对分析得到的评价结果得到类似的结果，但也在一部分月份表现出相反的结果，这是由于集对分析方法除了反应当前站点监测数据所表现出的水质信息，同时利用了更多的空间信息，考虑了两个站点之间监测信息的互相影响，评价结果更加合理.两个监测断面的水质评价结果显示伊洛河七里铺站的水质年际变化不太大，而花园口站的水质年际变化较大，这是由于伊洛河作为支流，导致水量和水质变化的因子较为稳定，对水质影响不大，而黄河作为中国第二大河，受到的中上游带来的不确定性影响较大，水质年际变化较为明显.

4 结语

本文通过构建水质指标实测值与对应评价标准之间的集对关系，计算联系度，进而确定水质等级，采用熵权法确定各指标的权重，有效避免了人为赋权的主观影响，得到了更加合理的评价结果.集对分析法原理易懂、计算简便、结果直观，适合大部分地区的水质评价.相比于其它水质评价方法，集对分析的评价结果更加真实客观.借用VBA编程对评价方法进行集成，能够高效地批量处理数据，直接输出评价结果，方便快捷.将计算方法集成在Visual Basic上，通过按钮和数据表格的形式更加智能便捷地实现其功能，以方便非编程专业研究人员的操作和实践，是下一步的工作方向.同时，本文对比了同一地区的两条河流水质监测站点的水质评价结果，分析了上下游关系以及河流规模对于断面水质的影响.

[1] 陈南祥,苏荣,曹文庚.基于熵权的集对分析法在土默特左旗地下水水质评价中的应用[J].干旱区资源与环境,2013,27(6):30-34.

[2] 张冉,孙宝盛,王永亮,等.黄河入海口水质评价与预测[J].环境工程学报,2013,(8):3089-3093.

[3] 姜云超,南忠仁.三种不确定性水质综合评价方法比较研究[J].干旱区资源与环境,2011,25(3):177-181.

[4] DAHIYA S, SINGH B, GAUR S, et al. Analysis of groundwater quality using fuzzy synthetic evaluation[J]. Journal of Hazardous Materials, 2007,147( 3):938-946.

[5] 孟宪萌,胡和平.基于熵权的集对分析模型在水质综合评价中的应用[J].水利学报,2009,40(3):257-262.

[6] 童英伟,刘志斌,常欢.集对分析法在河流水质评价中的应用[J].安全与环境学报,2008,(6):84-86.

[7] 叶斌.基于改进熵值法的内河水运评价研究[D].成都:成都理工大学,2012:15-16.

[8] 任化准,温忠辉,等.基于熵权的集对分析方法在地下水脆弱性评价中的应用[J].工程勘察,2010,(4):44-47.

[9] 郑志宏,魏明华.基于熵值法的改进集对分析水质模糊评价[J].河海大学学报,2013,41(2):136-139.

[10] 薛巧英.水环境质量评价方法的比较分析[J].环境保护科学,2004,30(124):64-67.

Application of Set Pair Analysis based on Information Entropy in Water Quality Evaluation——Take Zhengzhou as an example

CHEN Juan1， HONG Si-yang2， CHENG Tao2， JIAO Zhi-qian2

(1. South China Institute of Environmental Sciences, Ministry of Environmental Protection, Guangzhou 510655, China; 2.College of Water Science, Beijing Normal University, Beijing 100875, China)

This paper introduces set pair analysis based on information entropy, and the method is translated into VBA programming and then applied in Qilipu and Garden surface water monitoring sections’ water quality analysis in Zhengzhou city. The result of three monitoring years is calculated out by the program. Then the result is compared with the results calculated by other two methods. The comparison shows that the result of set pair analysis has better effect. Method based on VBA programming is easy to operate, and it is a relatively good technical support for water environment conservation and management decision.

water quality assessment; entropy weights; set pair analysis; VBA

2016-03-01

陈隽(1967-)，男,山西太原人，高级工程师, 主要从事水资源与水环境方面的研究.通讯作者：洪思扬(1990-)女，博士研究生，主要从事水资源系统分析方面的研究.

10.14182/J.cnki.1001-2443.2016.05.010

X824

A

1001-2443(2016)05-0449-06