激发态氢原子间的相互作用色散系数

许荣霞, 黄时中

(安徽师范大学物理与电子信息学院,安徽 芜湖 241000)



激发态氢原子间的相互作用色散系数

许荣霞, 黄时中

(安徽师范大学物理与电子信息学院,安徽 芜湖 241000)

以氢原子动态极化率的格林函数理论为基础, 借助归纳法解决了该理论体系中所涉及的复杂微分算子的运算问题, 导出了处于任一激发态的氢原子的多极动态极化率的解析表达式,从而解决了处于任意激发态的两个氢原子间的范德瓦尔斯相互作用色散系数的计算问题.作为本理论的应用,给出了氢原子n=4激发态的多极动态极化率的解析表达式，绘出了氢原子n=4激发态的电偶极、电四极和电八极极化率随光场频率变化的曲线图,计算了H(4s)-H(4s)体系的范德瓦尔斯相互作用色散系数.

氢原子;激发态;多极动态极化率;色散系数

近年来,随着激光冷却和囚禁技术的发展以及Bose-Einstein凝聚在若干原子体系中的实现,人们越来越关注原子间相互作用色散系数的研究[1-4]．由于原子间范德瓦尔斯相互作用色散系数可以表示为原子的多极动态极化率的积分[5,6],因而研究色散系数的一个基础性工作是计算原子的多极动态极化率.

氢原子间的范德瓦尔斯相互作用色散系数一直是人们的研究重点[7-11],因为氢原子既是可以精确求解的量子体系,也是研究碱金属原子以及其它原子体系的基础.2008年,Masili等[12-14]将研究多光子电离问题中所采用的稳定变分方法引入到氢原子极化率和相互作用色散系数的计算中, 提出了计算基态氢原子的多极动态极化率和相互作用色散系数的稳定变分方法,精确地计算了基态氢原子的极化率以及基态氢原子间的两体和三体相互作用色散系数,并将其视为原子间相互作用色散系数的“精度标杆”.然而,此方法的不足之处是只适用于基态,无法推广到激发态.2012年,方燕等利用径向库仑格林函数的积分性质[15]导出了处于第二激发态的氢原子的多极动态极化率的解析表达式，绘出了处于第二激发态的氢原子的电偶极、电四极和电八极动态极化率随光场频率变化的曲线图,计算了H(3s)-H(3s)体系的两体色散系数.

本文以方燕[15]等的研究工作为基础,借助归纳法解决该理论体系中所涉及的复杂微分算子的运算问题,导出处于任一激发态的氢原子的多极动态极化率的解析表达式,从而解决处于任意激发态的两个氢原子间的范德瓦尔斯相互作用色散系数的计算问题.作为本理论的应用,我们将给出氢原子n=4激发态的多极动态极化率的解析表达式，绘出氢原子n=4激发态的电偶极、电四极和电八极极化率随光场频率变化的曲线图,并具体计算H(4s)-H(4s)体系的范德瓦尔斯相互作用色散系数.

1 理论

两个氢原子A和B间的范德瓦尔斯相互作用势可以表示为[16，17]

(1)

其中R是两个原子核之间的距离，C2n是两体色散系数，可以表示为两个原子在虚光频时的动态极化率之积的积分[5,6]

(2)

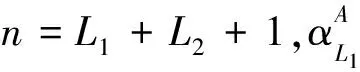
对于处在φnilimi态的氢原子, 其2l-极动态极化率的基本计算式是

(3)

按照方燕[15]等的工作,可以得到φnilimi态氢原子的多极动态极化率的如下表达式

(4a)

(4b)

(4c)

(4d)

(4e)

利用莱布尼茨公式无法导出此微分的一般表达式. 我们发现借助归纳法可以解决此问题. 依据对前5阶偏微分的表达式的总结,可以归纳出

(5a)

(5b)

(6)

对于n=1、2、3的情形, 由(6)和(4a)式所导出的氢原子多极动态极化率的解析表达式与之前方燕[15]等所导出的解析表达式完全一致，这也验证了一般解析式(6)的正确性.

2 应用

2.1 处于4s激发态的氢原子的多极动态极化率

图1 4s激发态的氢原子的动态偶极极化率Fig.1 Dynamic dipole polarizability of atomic hydrogen omic hydrogen in its 4s excited state

图2 4s激发态的氢原子的动态四极极化率Fig.2 Dynamic quadrupole polarizability of at in its 4s excited state

不难发现，在0.005-0.0237的频率范围内，对应着4个激发能：0.01124,0.01734,0.02106,0.02346,图中渐近线的位置与此相符.

2.2 H(4s)-H(4s)体系的两体色散系数

利用(2)式和Mathematic程序可以方便地计算出同处在4s激发态的两个氢原子之间的两体色散系数，计算结果列于表1中.

表1 H(4s)-H(4s)体系的两体色散系数(原子单位)

图3 4s激发态的氢原子的动态八极极化率Fig.3 Dynamic octupole polarizability of atomic hydrogen in its 4s excited state

3 结语

本文以氢原子动态极化率的格林函数理论为基础, 借助归纳法解决了该理论体系中所涉及的复杂微分算子的运算问题, 导出了处于任一激发态的氢原子的多极动态极化率的解析表达式, 从而解决了处于任意激发态的两个氢原子间的范德瓦尔斯相互作用色散系数的计算问题. 作为本理论的应用, 给出了氢原子n=4激发态的多极动态极化率的解析表达式，绘出了氢原子n=4激发态的电偶极、电四极和电八极极化率随光场频率变化的曲线图, 计算了H(4s)-H(4s)体系的范德瓦尔斯相互作用色散系数. 与之前所导出的氢原子第一、第二激发态的多极动态极化率的解析表达式作比较发现，我们所推导的一般解析式是正确的，可以为后续其他方法的研究提供很好的参考数据.

[1] LEGGETT A J. Bose-Einstein condensation in the alkali gases: Some fundamental concepts[J]. Rev Mod Phys， 2001,(73):307.

[2]〗MITROY J， BROMLEY M W J. Higher-order Cn dispersion coefficients for the alkali-metal atoms[J]. Phys Rev A, 2005,(71):042701.

[3] MITROY J, BROMLEY M W J. Higher-order Cn dispersion coefficients for hydrogen[J]. Phys Rev A, 2005,(71):032709.

[4] DEAL W J, YOUNG R H. The long-range interaction between two hydrogen atoms[J]. Mol Phys, 1970,(19):427-429.

[5] DALGARNO A, DAVISON W D. The calculation of Van der Waals interactions[J]. Adv At Mol Phys， 1966,(2):1.

[6] CEBIM M A, MASILI M， GROOTE J J D. High precision calculation of multipolar dynamic polarizabilities and two- and three-body dispersion coefficients of atomic hydrogen[J]. Few-Body Syst， 2009,(46):75.

[7] FIGARI G, MAGNASCO V. On the interpolation of frequency-dependent polarizabilities through a readily integrable expression[J]. Chem Phys Lett, 2003,(374):527.

[8] DEAL W J, YOUNG R H. Long-range interaction between two hydrogen atoms[J]. Mol Phys， 1970,(19):427.

[9] KOIDE A, MEATH W J, ALLNATT A R. Abinitio evaluation of multipole dispersion energies and properties[J]. J Phys Chem， 1982,(86):1222.

[10] MAGNASCO V, FIGARI G. One-center calculation of dispersion coefficients between ground-state H-atoms from pseudostate decomposition of static multipole polarizabilities[J]. Mol Phys， 1987,(62):1419.

[11] THAKKAR A J. Higher dispersion coefficients-accurate values for hydrogen-atoms and simple estimates for other systems[J]. J Chem Phys， 1988,(89):2092.

[12] GAO B, STARACE A F. Variational calculation of multiphoton ionization processes for the H atom[J]. Phys Rev Lett， 1988,(61):404.

[13] GAO B, STARACE A F. Variational principle for high-order perturbations with application to multiphoton processes for the H atom[J]. Phys Rev A， 1989,(39):4550.

[14] LIU C R， GAO B， STARACE A F. Variationally stable treatment of two-and three-photon detachment of H- including electron-correlation effects[J]. Phys Rev A， 1992,(46):5985.

[15] 方燕,黄时中.氢原子第二激发态的多极动态极化率和两体色散系数[J].原子与分子物理学报,2012,29(3):56.

[16] STANDARD J M, CERTAIN P R. Bounds to two- and three-body long-range interaction coefficients for S-state atoms[J]. J Chem Phys, 1985,(83):3002.

[17] PATIL S H, TANG K T. Multipolar polarizabilities and two-and three-body dispersion coefficients for alkali isoelectronic sequences[J]. J Chem Phys, 1997,(106):2298.

The Dispersion Coefficient of Atomic Hydrogen in the Excited States

XU Rong-xia, HUANG Shi-zhong

(College of Physics and Electrical Information, Anhui Normal University, Wuhu 241000, China)

Based on the Green function theory of dynamic polarizability for hydrogen atom, and with the aid of inductive method used to solve the complex differential operator involved in the theory, an analytical expression for the multipole dynamic polarizabilities of hydrogen atom in an arbitrary excited state is derived, so that the problem of calculating the van der Waals interaction dispersion coefficient between two excited hydrogen atoms is solved. As an application of the present theory, the multipole dynamic polarizabilities of hydrogen atoms in n=4 excited state are calculated, typical results for dynamic dipole, quadrupole and octupole polarizabilities at real photon frequencies are shown in a series of figures. Meanwhile, the two-body dispersion coefficients for H(4s)-H(4s) system are computed.

hydrogen； excited state； multipole dynamic polarizabilities； dispersion coefficients

2015-03-30

国家自然科学基金专项基金项目(11047019)；安徽省自然科学基金项目(11040606M15).

许荣霞(1990-)，女，安徽舒城县人，硕士研究生；黄时中(1959-)，男，安徽宿松县人，教授，硕士生导师.

10.14182/J.cnki.1001-2443.2016.05.007

O562.4

A

1001-2443(2016)05-0437-04