基于变权AHP法的贫困生评定

彭德军，杨婧宇，沈有建

（海南师范大学 数学与统计学院，海南 海口 571158）

基于变权AHP法的贫困生评定

彭德军，杨婧宇，沈有建

（海南师范大学 数学与统计学院，海南 海口 571158）

文章应用多属性决策理论研究高校贫困生评定问题.通过确定贫困生评定的指标集，对定性指标采用模糊分级量化法，并对各指标值进行无量纲化处理.采用层次分析法（AHP）获取属性权重向量，建立变权AHP综合评价模型，得到了综合评价结果，较传统的评价方法更为客观、更具科学性.

学生资助；贫困生；层次分析法；变权

在贫困生评定过程中，需要对多个属性指标进行分析.定量指标的数据（如收入、支出）容易获得，根据不同指标类型（如：效益型、成本型、偏离型），可以直接对定量指标进行无量纲化.定性指标则需要先进行定量化处理，再进行无量纲化.徐泽水[1]、胡苗苗等[4]介绍了效益型和成本型评价指标，并给出了这两类指标的无量纲化公式.冯春明等[2]对贫困生评定采用AHP法，根据权重大小对贫困程度进行排序.方楠[3]应用熵权多指标模糊系统处理贫困生的评定问题，但对定性指标和定量指标处理的方法未介绍，并且缺少对贫困生各项指标均衡性考虑.张昭[5]采用组织小组评议方式对定性指标进行处理（以1～9数字为标度值）.杨昔阳等[6]引进了变权公理，提升了综合评价中各指标的均衡性.陈峰[7]以1～3分为标度的打分模式对定性指标进行处理.徐亮[8]对学生资助综合评价的重点是指标体系的预处理，权重的获得方法，并且考虑了各指标的均衡性.但对于非收入、支出型的定性评价指标（如：家人健康、家庭特征、负债情况等）的处理方法并未涉及.本文在传统AHP方法的基础上，采用文献[5]的方法对定性指标作量化处理，再进一步对指标值进行无量纲化，即定性指标值无量纲化处理，建立了较传统评价方法更为客观的变权AHP贫困生综合评价模型.

1 贫困生评定决策方法介绍

贫困生评定属于多属性决策问题，采用如下做法：第一步，确定评价指标，获得决策矩阵，并对决策矩阵进行无量纲化处理.对于可获得具体数值的如收入、支出等指标，通过发放问卷获得数据，并做无量纲化处理.对于带模糊性的定性指标，可通过组织小组评议对调查对象进行1～9标度值打分，由此达到对定性指标

量化.再对非收入型指标作量化处理.第二步，确定权重，本文对该问题进行分层分析，利用层次分析法获得权重.第三步，建立基于变权AHP的综合评价模型.第四步，排序择优，按综合属性值进行排序，由此得到贫困程度高低排序.

1.1 贫困生评定指标的确定

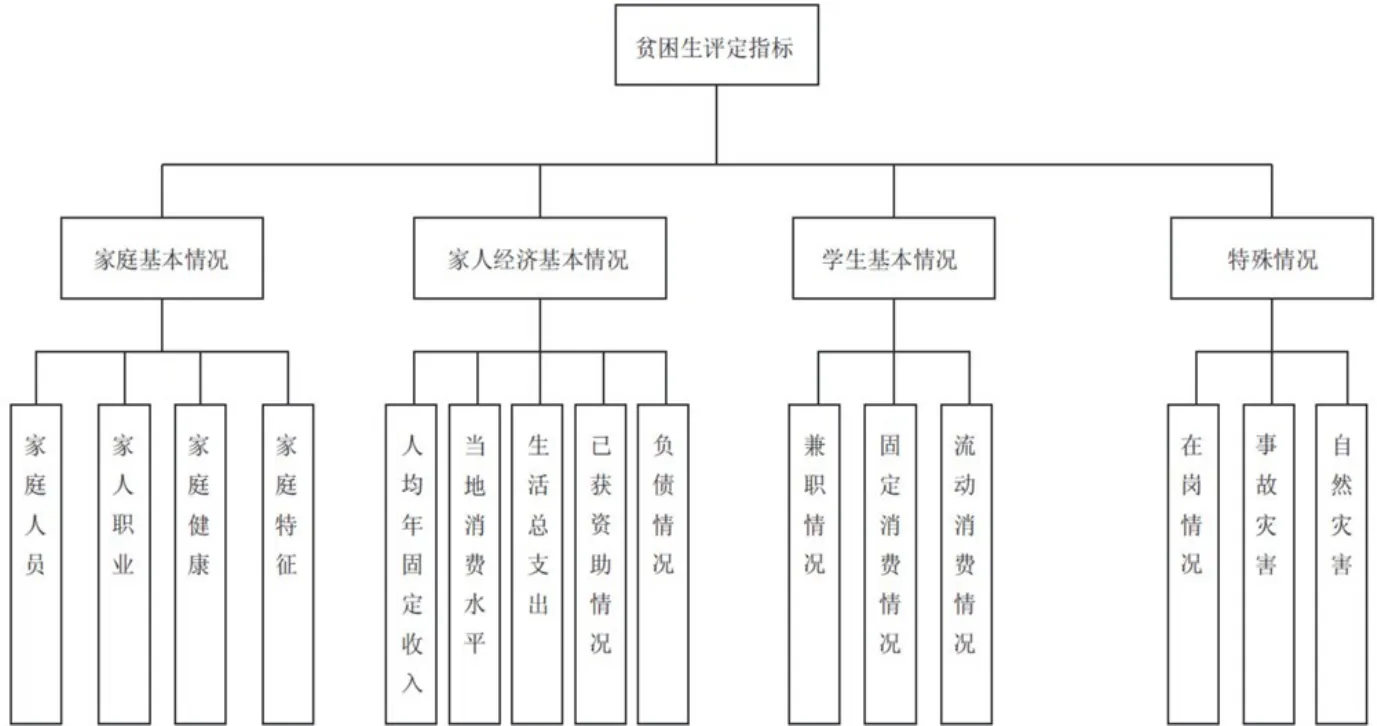
图1 贫困生评价指标体系Fig.1 Evaluation index system for poor students

建立包括家庭基本情况（B1）、家人经济基本情况（B2）、学生基本情况（B3）和特殊情况（B4）在内的4个一级指标：A={B1，B2，B3，B4}.

家庭基本情况（B1）包括家庭人员C11、家人职业C12、家人健康C13、家庭特征C14等4个二级指标：B1={C11，C12，C13，C14}.

家人经济基本情况（B2）包括固定收入C21、生活总支出C22、当地消费水平C23、已获资助情况C24和负债情况C25等5个二级指标：B2={C21，C22，C23，C24，C25}.

学生基本情况（B3）包括兼职情况C31、固定消费情况C32、流动消费情况C33等3个二级指标：B3={C31，C32，C33}；

特殊情况（B4）包括在岗情况C41、事故灾害C42、自然灾害C43等3个二级指标：B4={C41，C42，C43}.

1.2 评价指标无量纲化处理

首先，对评价指标进行分析，具体说明见表1.

1.2.1 定量指标无量纲化处理

上述确定的定量指标类型可分为三种：效益型、成本型和偏离型.对于效益型指标，属性值越大贫困程度越高；成本型指标，属性值越小贫困程度越低；偏离型指标，属性值越偏离某个固定值贫困程度越高.由于不同指标的属性值的量纲不同，各属性值之间不具可比性，需要对定量指标作无量纲化处理.

1）效益型评价指标.效益型指标有当地消费水平C22、生活总支出（万元）C23.其中当地消费物价指数参考各省市统计局2015年国民经济和社会发展统计公报数据中CPI数值.生活总支出，通过调查问卷获得数据，包括最基本的子女生活费年支出、医疗支出、家人生活费年支出、学校学杂费支出.决策矩阵规范化处理：

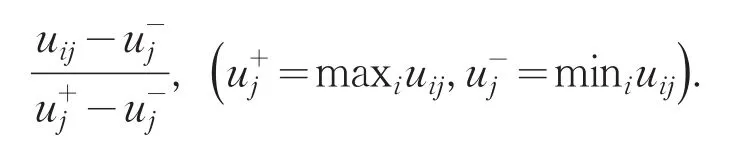
2）成本型评价指标.成本型指标有固定收入（万元）C21、固定消费情况（元）C32、流动消费水平C33（元）、在岗情况C41，其中固定消费情况、流动消费水平、在岗情况等指标通过调查问卷获得数据.固定消费情况包括学生饮食年消费情况和固定资产，流动消费情况为学生生活费支出和学生饮食年消费之差.决策矩阵规范化处理：

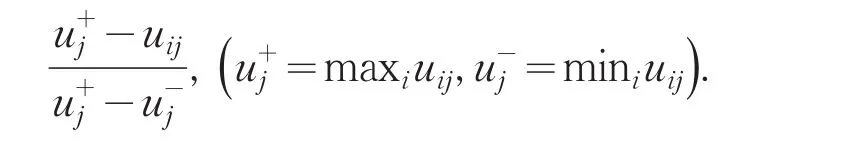
表1 一、二级指标分析表格Tab.1 The first and sencond level index analysis form

3）偏离型评价指标.偏离型指标有家庭人员C11，一般认为独生子女家庭经济压力情况较轻，贫困程度相对较低，而家庭人员总数少于或大于3人的，家庭经济压力较重，认为其贫困程度较高，由此认为家庭人员偏离3的程度越大，贫困程度越高.决策矩阵规范化处理：

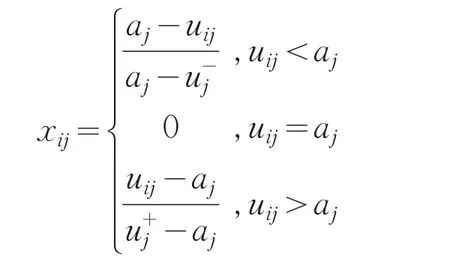
1.2.2 定性指标无量纲化处理

对于剩下的评价指标如：家人职业C12、家人健康C13、家庭特征C14、已获资助情况C24、负债情况C25、兼职情况C31、自然灾害C42、事故灾害C43.这些指标不能直接得到具体的数据数值，并且带有较强的主观性和模糊性，属于定性指标的范畴，可以采用模糊分级量化方法，原理如下：将指标划分等级，用数字1～9为标度范围进行标度，标度值越大，贫困程度越高.

定性指标量化.为此制作的分级量化表格见表2.

定性指标无量纲化.定性指标量化后，为统一量纲，对量化后的定性指标值进行无量纲处理，效益型指标有家人职业、家庭特征、已获资助情况、负债情况、兼职情况、自然灾害、事故灾害等指标.特点是标度值越大，贫困程度越高.成本型指标有家人健康指标，特点是标度值越小，贫困程度越高.

1.3 指标权重的确定

指标权重的确定采用层次分析法，具体步骤如下：

1.3.1 建立递阶层次结构

在应用层次分析法处理复杂决策问题时，需建立层次分析结构模型.在这个模型中，复杂的决策问题分解为被称为元素的组成部分，再按属性将元素进行分组，这是一种递阶关系.层次的分类包含目标层（只有一个指标元素，为总的目标要求）、准则层（中间环节，可由若干层次组成）、方案层（可供选择的各种措施，备选方案）.

1.3.2 构造比较判断矩阵

按照表3所示1～9标度进行相对重要程度赋值，记为aij.对于准则A，通过下层n个被比较元素可构成一

个两两比较的判断矩阵：A=（aij）n×n.在该式子中，元素aij表示单一原则A中元素Ai与Aj的相对重要性的1～9标度量化值.注意:对于一个由n个元素构成的判断矩阵只需n（n-1）/2个判断即可.

表2 非收入评价指标分级量化Tab.2 Hierarchical quantization of the non-income evaluation indices

表3 1～9标度含义Tab.3 The meaning of the scales 1～9

1.3.3 层次单排序及一致性检验

1）层次单排序.层次单排序主要是每个判断矩阵各因素在其准则下的相对权重，即对权向量的计算，其中最常用的有和积法、方根法.在这里应用和积法.

和积法计算步骤：

2）一致性检验步骤：

（2）查找相应n的平均随机一致性指标RI（random index），见表4：

表4 平均随机一致性指标Tab.4Mean random consistency index

当CR＜0.1时，认为判断矩阵一致性可接受.当CR≥0.1时，认为判断矩阵一致性检验不可接受.需重新修正.

1.3.4 层次分析法应用

由1.3.2节方法，构造两两比较判断矩阵.对于一级指标A，判断矩阵为：

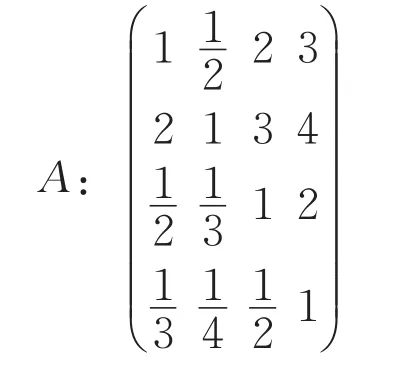
其中，行和列的指标顺序为{B1，B2，B3，B4}.对于二级指标，判断矩阵分别为：

其中，各判断矩阵行和列指标的顺序分别为：B1，{C11，C12，C13，C14}；B2，{C21，C22，C23，C24，C25}；B3，{C31，C32，C33}；B4，{C41，C42，C43}.

根据上述和积法，计算得到各级指标权重.

一级指标A：家庭基本情况、家人经济基本情况、学生基本情况和特殊情况权重；A=[0.2662，0.4673，0.1601，0.0954].二级指标A1：家庭基本情况包括家庭人员、家人职业、家人健康、家庭特征指标权重；A1= [0.0884，0.2393，0.4330，0.2393].二级指标A2：家人经济基本情况包括固定收入、生活总支出、当地消费水平、已获资助情况和负债情况权重；A2=[0.4372，0.1538，0.0896，0.0549，0.2645].二级指标A3：学生基本情况包括兼职情况，固定消费水平，流动消费水平权重；A3=[0.1220，0.5584，0.3196].二级指标A4：特殊情况包括失业情况，事故灾害，自然灾害二级指标权重；A4=[0.1634，0.2970，0.5396].

表5 权向量获得及一致性检验Tab.5 Weight vector achievement and consistency test

一致性检验结果见表5.

2 变权综合评价

对应的变权综合模式为：

基于对贫困生各项指标均衡性考虑，构造满足均衡性要求的变权公式：

其中wj为常值权重.当α＜1/2时，各指标平衡问题考虑较多；当α＜1/2时，有一定可容忍缺陷.这里取α=1/2.

3 贫困生评定工作的具体实例应用

一共发放30份贫困生调查问卷，剔除11份，余下19份为贫困生申请对象.将19个对象依次编号.对非收入支出几项，组织小组评议.表6是原始数据，无量纲化数据，以及综合属性值.

经过定量与定性型指标的处理.再进行变权综合评价得到学生家庭基本情况指标B1（见表6）.采用类似的方法可获得学生家庭经济基本情况指标B2：{0.1653，0.4783，0.6311，0.3762，0.6521，0.5450，0.6697，0.5797，0.6493，0.6927，0.4273，0.3564，0.6468，0.7388，0.6479，0.2159，0.2719，0.5846，0.7599}；学生基本情况指标B3：{0.1343，0.8200，0.7202，0.6554，0.8436，0.6476，0.7343，0.8748，0.8688，0.9370，0.3786，0.3501，0.7374，0.4821，0.7713，0.5341，0.6146，0.8743，0.4602}；学生特殊情况指标B4：{0.3610，0.3940，0.1520，0.4563，0.3005，0.2475，0.5345，0.3753，0.2162，0.4306，0.1850，0.2658，0.9019，0.5267，0.8826，0.2133，0.2078，0.3301，0.4285}.

经过变权综合评价.得综合属性为：{0.1454，0.6054，0.5950，0.4335，0.6051，0.5148，0.6295，0.5449，0.6521，0.7151，0.3078，0.2637，0.6131，0.5916，0.7214，0.2602，0.3613，0.5691，0.6519}.

综合排序情况：{15，10，9，19，7，13，2，5，3，14，18，8，6，4，17，11，12，16，1}.

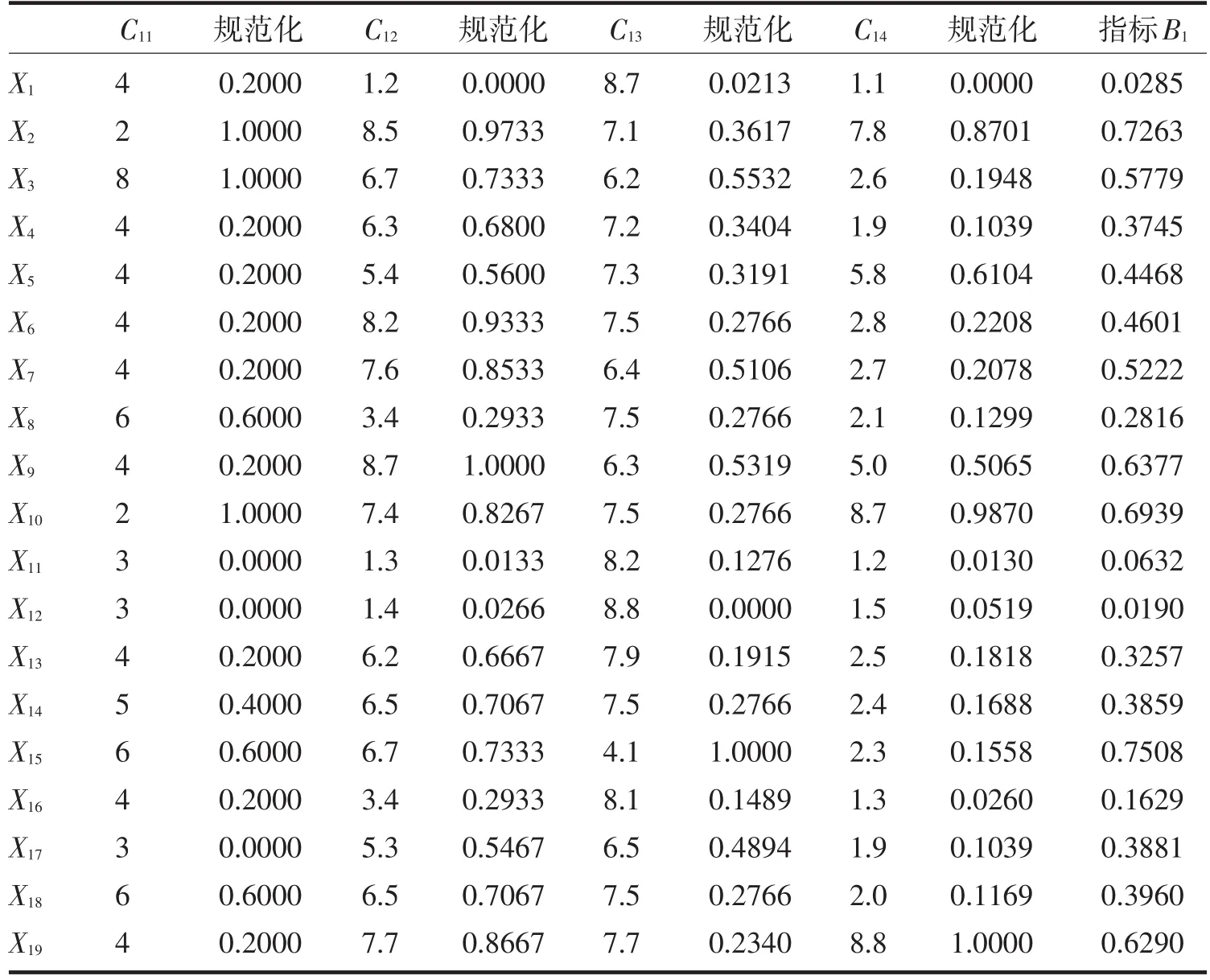
表6 19位学生家庭基本情况数据表格Tab.6 Data table of the 19 students’family situation

由此可以认定，在19名贫困生申请者中，编号15的学生贫困程度最高.

[1]徐泽水.不确定多属性决策方法及应用[M].北京：清华大学出版社，2004.

[2]冯春明，杨玉杰.层次分析法在高校贫困生评定工作中的应用[J].聊城大学学报（自然科学版），2014，27（4）：106-110.

[3]方楠.基于熵权的多指标模糊系统在高校贫困生评定中的应用[J].四川教育学院学报，2009，25（7）：29-33.

[4]胡苗苗，朱佳敏.基于多属性决策的高校家庭经济困难学生认定方法及应用[J].重庆工商大学学报（自然科学版），2016，33（2）：55-57.

[5]张昭.基于综合评价理论的高校家庭经济困难学生的认定研究[D].武汉：武汉理工大学，2009.

[6]杨昔阳，曾丽雪.合理变权的层次分析模型[J].泉州师范学院学报（自然科学版），2009，27（2）：19-24.

[7]陈峰.基于AHP的家庭经济困难学生评价指标体系研究[J].开封教育学院学报，2013，33（4）：58-63.

[8]徐亮.综合评价理论在学生资助工作中的运用[J].产业与科技论坛，2015，14（23）：211-213.

责任编辑：吴兴华

The Evaluation of Poor Students Based on the Variable-weight AHP Method

PENG Dejun，YANG Jingyu，SHEN Youjian
（School of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

An assessment of poor students in colleges and universities is researched by using multiple-attribute decisionmaking theorem.The assessment index set is determined,qualitative index is quantized by fuzzy hierarchical quantization method and then is nondimensionalized.Using analytic hierarchy process to obtain attribute weight vector,the comprehensive evaluation model based on variable weight AHP is established,and comprehensive evaluation result is achieved.This model is more objective and scientific than traditional method.

student aid；poor student；analytic hierarchy process；variable-weights

G 647

A

1674-4942（2016）03-0256-07

2016-06-11

海南省教育厅高等学校科学研究基金项目（Hjkj2013-21）