爆破振动信号的局部波分解方法

徐振洋，陈占扬，郭连军，于妍宁

（1.辽宁科技大学 矿业工程学院，辽宁 鞍山114051；2.北京理工大学机电学院 爆炸科学与技术国家重点实验室，北京100081）

爆破振动信号的局部波分解方法

徐振洋1，陈占扬2，郭连军1，于妍宁1

（1.辽宁科技大学 矿业工程学院，辽宁 鞍山114051；2.北京理工大学机电学院 爆炸科学与技术国家重点实验室，北京100081）

针对爆破振动信号具有非线性、随机性较强的特点，提出利用局部波分解（Local Mean Decomposition，LMD）处理并分析爆破振动信号。结合露天铁矿逐孔起爆方式下爆破振动测试信号分析，研究信号的时频及能量分布特征。结果表明：LMD方法能完整地分解重构爆破信号，有效减少模态混叠现象，更加真实反映信号的原始信息；相比经验模态分解方法（Empirical Mode Decomposition，EMD）、LMD方法的端点效应轻微，具有较高的解调精度；LMD方法可以精确分析振动能量的分布规律，有利于进一步识别爆破本身的力学作用特征。

爆破振动；爆炸力学；信号分析；局部波分解；能量

1 引言

爆破振动信号是一种非线性的随机信号，蕴含了爆破过程的大量重要信息，能够反映爆破设计与爆破地质的本质特征﹝1-2﹞。对于爆破振动信号的分析开展已久，常见的信号分析方法有傅里叶变换、小波变换、Hilbert-Huang变换等﹝3-5﹞。傅里叶变换处理非平稳信号时，无法计算瞬时频率与时间的变化情况，因此难以揭示信号在某一时刻的本质特征；小波变换严重依赖于所选取的小波基，小波基的选择全凭主观经验无自适应性；Hilbert-Huang变换存在如模态混叠、端点效应与信息丢失等问题﹝6-7﹞。

2005年，SMITH J S提出了局部均值分解（Local Mean Decomposition，LMD）方法﹝8﹞。LMD方法具有较好的分析非线性、非平稳信号的能力，已在脑电信号分析和机械故障诊断领域得到了应用﹝9-10﹞。爆破振动信号的随机性和受到的干扰都较大地超过了机械故障信号，后者关注的是信号的突变特征，而分析爆破振动信号不但需要研究局部信息，也需将爆破振动全过程的时频信息进行提取，所以，爆破振动信号的分析有必要引入一种高分解精度的自适应信号处理技术。

2 局部均值分解理论

LMD方法自适应地将一个复杂非平稳的多分量信号分解为若干个瞬时频率具有物理意义的乘积函数（Product Function，PF）之和，其中每一个PF分量由一个包络信号和一个纯调频信号组成。包络信号就是PF分量的瞬时幅值，而PF分量的瞬时频率则可以由纯调频信号直接求出，进一步将所有PF分量的瞬时幅值和瞬时频率组合，便可以得到原始信号的完整时频分布。

2.1 基本过程

对任意信号x（t），其LMD分解过程如下﹝8﹞：

（1）找出信号所有的局部极值点ni，再计算相邻两个极值点ni与ni＋1的局部均值mi、局部包络估计值ai。计算公式如下：

（2）将所有局部均值mi用直线依次连接，然后用滑动平均法进行平滑处理，得到局部均值函数m11（t）。同理，将所有局部包络值ai（t）依次连接，然后用滑动平均法进行平滑处理，得到局部包络函数a11（t）。用原信号x（t）减去局部均值函数m11（t）得到，用h11（t）除以局部包络函数a11（t）实现解调：

（3）判断s11（t）是否为纯调频信号，即他的包络函数a11（t）是否满足条件a11（t）＝1，如果不满足，将s11（t）作为新信号重复步骤（1，2），直到s1n（t）为纯调频信号，在实际中可设定一个变动量Δ，a1n（t）＝1时，有以下关系：

（4）迭代结束，将迭代过程中所得的全部包络估计函数相乘得到瞬时幅值函数a1（t），再将a1（t）和纯调频信号s1n（t）相乘得到第一个PF分量：

（5）由纯调频信号s1n（t）求瞬时频率f1（t）：

式（6）将PF1从x（t）中分离出一个新的信号u1（t），把u1（t）当作原始信号重复步骤1～4，直到un（t）为常数或单调函数为止，从而将x（t）分解为n个PF分量和un（t），有：

2.2 算法的端点效应

EMD方法取所有极值点进行三次样条函数拟合，当端部数据不是极值点或获取的极值点存在误差时，分解过程中就会存在虚假分量﹝11﹞。LMD算法中的PF分量采用除法运算取得，而EMD算法中的IMF分量采用减法运算取得，因此，对一个较为复杂信号进行分解时，LMD比EMD获得的分量会少，这在一定程度上也抑制了虚假分量的产生。

2.3 信号时频分布

每一个PF分量均由一个包络信号和一个纯调频信号相乘得到，其中包络信号为PF分量的瞬时幅值，且PF分量的瞬时频率可由纯调频信号得到，每一个分量都具有其物理意义。通过局部均值分解直接获得信号的瞬时幅值和瞬时相位，即得到了信号相应的时频分布。同时，利用传统的Hilbert变换或者能量算子解调方法对每个PF分量进行解调同样也可以获得相应的时频分布。

采用Hilbert变换计算信号的时频分布，当得到分解后的PF分量以后，对每一个PF分量做Hilbert变换：

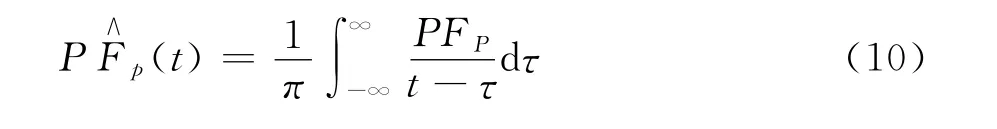
然后构造解析信号：

信号的瞬时幅值为：

信号的相位为：

信号的瞬时频率为：

信号的时频谱为：

这里省略了残量rn，RP表示取实部。H（ω，t）为信号在时域与频域上的变化。

3 仿真信号分析

在EMD的分析中可知，任意随机信号都可以分解为一系列平稳信号与随机信号的叠加﹝12-13﹞。取多周期信号x（t），模拟逐孔起爆方式下产生的振动信号的多次触发，以此验证LMD方法处理爆破振动信号的正确性。

式中：t＝［0，1］，信号采样频率为1 024 Hz。

该信号由非线性调频-调幅信号x1和x2组成，波形如图1所示。

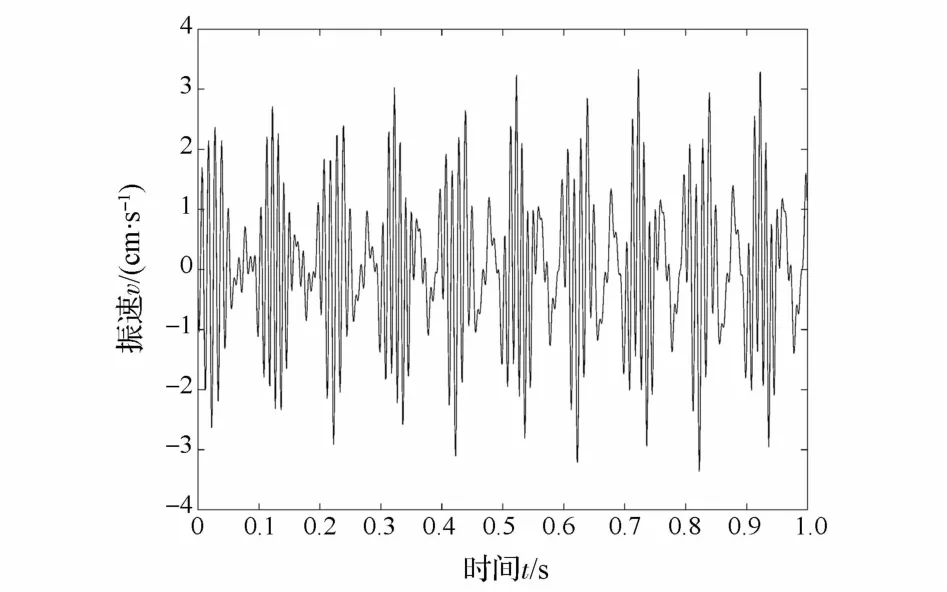
图1 信号原始波形Fig.1 Original waveform

首先采用EMD方法对信号x（t）进行分解，分解出的结果如图2所示。

图2 信号EMD分解结果Fig.2 The results of EMD decomposition

从图2中可以看出，经过EMD分解，共得到了7个IMF分量，其中，前两个分量对应原始信号中的调制信号，但是信号端部有明显的变形。分解过程中出现了较多虚假分量，即事实上并不存在的分量IMF3～IMF7。

用LMD方法对x（t）进行分解，结果如图3所示。

图3 信号LMD分解结果Fig.3 The results of LMD decomposition

经过LMD分解，得到3个PF分量，PF1分量对应了原信号中载频为100 Hz的调频-调幅信号部分；第二个分量PF2，对应了原信号中载频为25 Hz的调幅-调频分量；余量PF3比较小且接近为零。

从图3中可以看出，LMD方法精确分离了原始信号中所包含的振动分量，且分解出的分量幅值和频率基本没有变化，没有出现大量的虚假分量，为精确分析信号所含信息奠定了基础。

4 工程实例验证

4.1 工程概况

鞍钢齐大山铁矿以磁铁矿、绿泥岩、混合岩为主，采用露天台阶爆破方法开采，使用逐孔起爆方式实现多炮孔的延时顺序起爆。台阶高度12 m，孔距为7.5 m，排距为6 m，钻孔直径为250 mm，超深为1.5m；使用混装乳化与铵油炸药，炸药爆速为5 200 m/s。爆破网路如图4所示。

图4 爆破网路Fig.4 Blasting network

4.2 爆破振动信号监测方案

测试目的在于验证LMD方法对爆破振动信号分析的可靠性，故选择了较为简单的爆破振动测试方法，旨在获取实际爆破振动波形。在爆破台阶选择较平整场地，测振仪布置在最后炮孔延长线上。3个测点之间距离较为接近，位于远离起爆点的一侧，并且距离爆区也较近，信号的波形会相对复杂，可以更好地测试LMD方法对信号的解调精度。爆破振动测试仪布置示意图如图5所示。

图5 测点布置示意图Fig.5 Layout of monitoring points

4.3 监测数据

选择较平整场地进行爆破振动监测，爆区岩石以混合岩为主，测振仪沿直线布置，间隔为60 m、73 m、89 m，监测结果如表1所示，波形图如图6所示。

表1 振动监测结果Table 1 Monitoring results

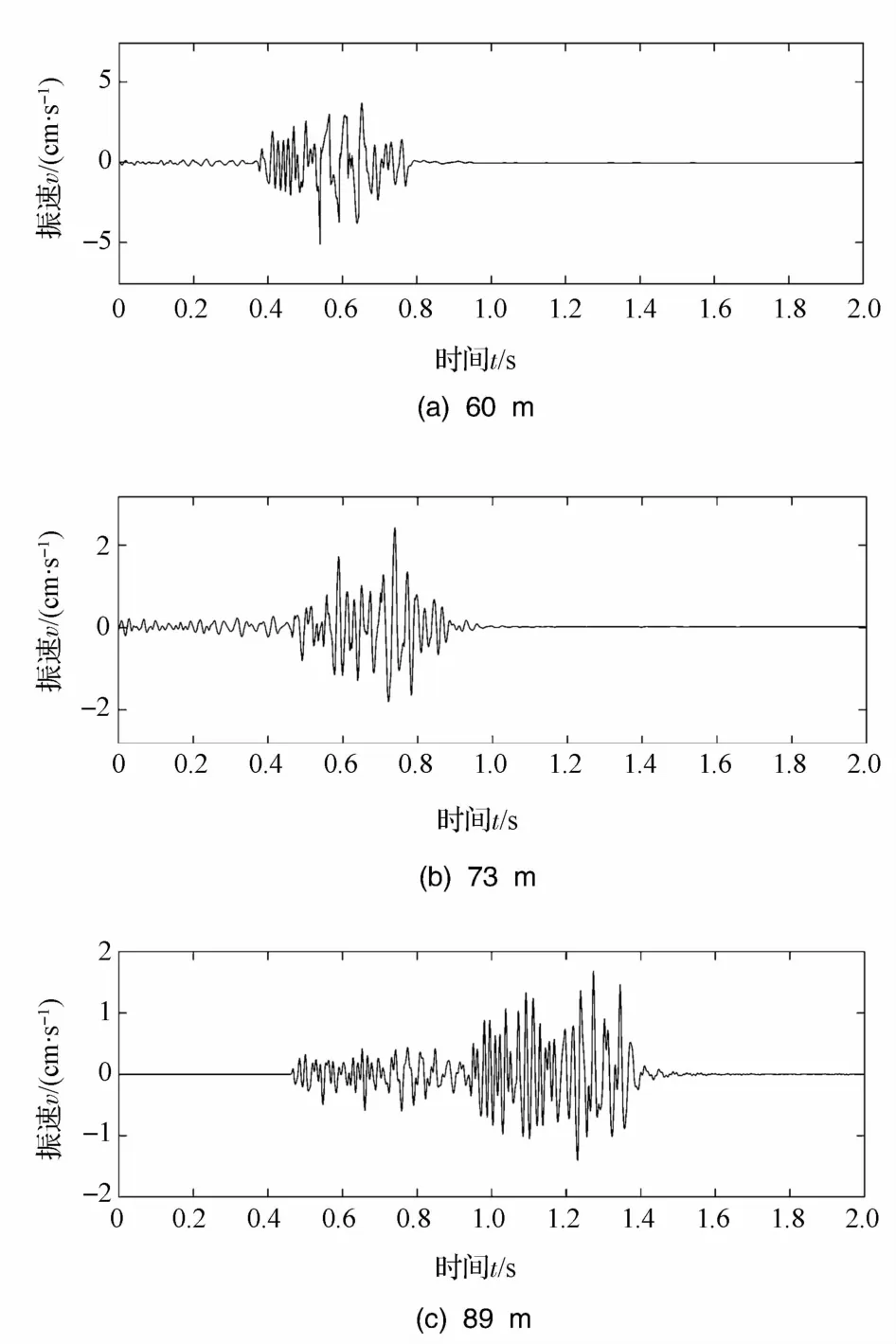
图6 监测波形Fig.6 Monitoring waves

由表1可看出，振速峰值相差不大，主振频率较为接近。一般的爆破振动测点布置距离爆区较远，但爆区后方的边坡在爆破中受到的影响最大，如果LMD方法可对爆破近区信号进行更好地分析，对爆破振动对边坡的危害也具有重要的参考价值。

5 爆破振动信号能量的LMD分析

经过EMD分解得到的IMF，可能会产生一些不具备实际物理意义的分量，LMD方法解决了该问题，而且LMD更加适合处理非平稳、非线性信号﹝14﹞。

振动信号能量与时间-频率的对应关系如图7所示。目前广泛使用的逐孔起爆技术，更加客观地表征了爆破振动信号的叠加特性。3个测点之间的距离均在20 m之内，但仍然能够清晰地识别出，随测点距离的增加，爆破振动能量在向低频部分转移（见图7），也证明了逐孔起爆技术的优势，随着振动传播距离的增加，虽然振动能量向低频发展，但能量峰值衰减的更为快速，有利于保护爆区后方边坡的完整性﹝13﹞。测点布置在起爆点的另一侧，使得炮孔起爆后经过了一定距离的传播，传播过程中伴随着岩体的损伤与破碎，信号在此基础上叠加，可以看出，能量谱中波峰非常密集，每个能量的峰值能够精确到在0.1 Hz上的分布。实际0.1 Hz也是一个频带，而EMD方法给出的能量谱仅能表征能量在1 Hz频带上的分布。以0.1 Hz为单位来观察，爆破振动能量的分布非常分散，LMD方法计算出的能量谱模态混叠现象非常轻微，而且从0 Hz开始已经产生了分布，有效避免了端点处的信息丢失，计算出的能量分布准确度更高，有利于精确的时频分析。

图7 LMD三维时频关系Fig.7 Three-dimensional energy spectrum using LMD

采用EMD方法的3个信号三维时频关系，如图8所示。

图8 EMD三维时频关系Fig.8 Three-dimensional energy spectrum using EMD

从图8可以看出，EMD计算出的数据和LMD有较大区别，接近0 Hz的频带内基本无数据出现，主要是EMD的端点效应使得起始部分的信号丢失。EMD方法是以1 Hz为单位进行计算，分解精确度低于LMD方法，模态混叠现象也较多，而分析爆破振动正是需要精确地区分细小频带内的信息。

由此看出，LMD方法在爆破振动信号的分析中有较大优势。分解的精度更高，有效抑制了处理过程中的端点效应。LMD方法和EMD方法类似，同样以基于极值点为基础，由此定义局域均值函数和局域包络函数，主要的不同点在于LMD方法使用滑动平均代替三次样条插值，最终将信号分解为一系列单分量的调频调幅信号，迭代次数少，运算速度较快，PF分量比IMF分量含有更多的频率和包络信息，由此抑制了信号分解的端点。LMD的时频分解使得能量分布更加真实，且没有产生EMD计算中的产生负频率现象。

6 结论

（1）LMD方法具有较好的时频分析性能，其分解具备自适应性，适合随机性较强的爆破振动分析，具有很好的完备性和可重构性。

（2）LMD在分解过程中，信号信息较少有损失和泄露，每个PF分量都由包络信号与纯调频信号的乘积构成，具有明确的物理意义。

（3）LMD方法有效地抑制了分解过程的端点效应，重构信号信息完整，具有较高的解调精度。

（4）LMD方法可以将细小频率上能量变化表现的十分清晰，爆破振动信号的三维时频图峰值非常尖锐、密集，峰值之间没有混叠，有利于进一步识别爆破振动携带的能量。

（

）：

﹝1﹞李夕兵，凌同华，张义平.爆破震动信号分析理论与技术［M］.北京：科学出版社，2009：226-239. LI Xi-bing，LING Tong-hua，ZHANG Yi-ping.Analysis of blast vibration signals-theories and methods［M］. Beijing：Science Press Ltd.，2009：226-239.

﹝2﹞言志信，彭宁波，江平，等.爆破振动安全标准探讨［J］.煤炭学报，2011，36（8）：1 281-1 284. YAN Zhi-xin，PENG Ning-bo，JIANG Ping，et al.Research about blasting vibration safety criteria［J］.Journal of China Coal Society，2011，36（8）：1 281-1 284.

﹝3﹞唐飞勇，王意堂，梁开水.爆破振动信号特征分析的应用探讨［J］.爆破，2010，27（4）：110-115. TANG Fei-yong，WANG Yi-tang，LIANG Kai-shui. Characteristics analysis of blasting vibration signals of open pit［J］.Blasting，2010，27（4）：110-115.

﹝4﹞中国生，房营光，徐国元.基于小波变换的建（构）筑物爆破振动效应评估研究［J］.振动与冲击，2011，28（8）：121-124. ZHONG Guo-sheng，FANG Ying-guang，XU Guoyuan.Study on blasting vibration effect assessment of structure based on wavelet transform［J］.Journal of Vibration and Shock，2011，28（8）：121-144.

﹝5﹞徐振洋，杨军，陈占扬，等.爆破地震波能量分布研究［J］.振动与冲击，2014，33（11）：38-42. XU Zhen-yang，YANG Jun，CHEN Zhan-yang，et al. Blasting seismic waves energy distribution study based on EEMD［J］.Journal of Vibration and Shock，2014，33（11）：38-42.

﹝6﹞HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences，1998，454：903-995.

﹝7﹞HUANG N E，WU Z H，LONG S R，et al.On instantaneous frequency.Advances in adaptive data analysis［J］.World Scientific，2009，1（2）：177-229.

﹝8﹞SMITH J S.The local mean decomposition and its application to EEG perception data［J］.Journal of the Royal Society Interface，2005（2）：443-454.

﹝9﹞RANDALL R B，ANTONI J，CHOBSAARD S.The relationship between spectral correlation and envelope analysis in the diagnostics of bearing faults and other cyclostationary machine signals［J］.Mechanical Systems and Signal Processing，2001，15（5）：945-962.

﹝10﹞程军圣，张亢，杨宇，等.局部均值分解与经验模式分解的对比研究［J］.振动与冲击，2009，28（5）：13-16. CHENG Jun-shen，ZHANG Kang，YANG Yu，et al. Comparison between the method of local mean decomposition and empirical mode decomposition［J］.Journal of Vibration and Shock，2009，28（5）：13-16.

﹝11﹞许宝杰，张建民，徐小力，等.抑制EMD端点效应方法的研究［J］.北京理工大学学报，2006，26（3）：196-200. XU Bao-jie，ZHANG Jian-min，XU Xiao-li，et al.A study on the method of restraining the ending effect of empirical mode decomposition（EMD）［J］.Transactions of Beijing Institute of Technology，2006，26（3）：196-200.

﹝12﹞HUANGN E，WU M L C，LONG S R，et al.A confidence limit for the empirical mode decomposition and Hilbert spectral analysis［J］.Proceedings of the Royal Society of London.Series A：Mathematical，Physical and Engineering Sciences，2003，459：2 317-2 345.

﹝13﹞于妍宁，徐振洋，郭连军，等.岩石动态特性对爆破振动能量分布的影响［J］.爆破器材，2015，44（6）：16-19. YU Yan-ning，XU Zhen-yang，GUO Lian-jun，et al. The influence of rock dynamic characteristics on distribution of blasting vibration［J］.Explosive Materials，2015，44（6）：16-19.

﹝14﹞程军圣，杨宇，于德介.一种新的时频分析方法局域均值分解方法［J］.振动与冲击，2008，27（S）：129-131. CHENG Jun-sheng，YANG Yu，YU De-jie.A new time frequency analysis method—the local mean decomposition method［J］.Journal of Vibration and Shock，2008，27（S）：129-131.

﹝15﹞王振宇，梁旭，陈银鲁，等.基于输入能量的爆破振动安全评价方法研究［J］.岩石力学与工程学报，2010，29（12）：2 492-2 499. WANG Zhen-yu，LIANG Xu，CHEN Yin-lu，et al.Study of safety evaluation method of blasting vibration based on input energy［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29（12）：2 492-2 499.

LMD method using in blasting vibration signal analysis

XU Zhen-yang1，CHEP Zhan-yang2，CUO Lian-jun1，YU Yan-ning1
（1.CoIIege of Mining Engineering，University of Science and TechnoIogy Liaoning，Pnshan 114051，Liaoning，China；2.State Key Laboratory of ExpIosion Science and TechnoIogy，SchooI of MechatronicaI Engineering，Beijing Institute of TechnoIogy，Beijing 100081，China）

According to the characteristic of higher randomness and larger interference of blasting vibration signal，blasting vibration signal was analyzed using Local Mean Decomposition（LMD）method.The signal amplitude frequency and energy distribution feature were investigated in detail combined with Open-pit Iron Mine of hole by hole blasting vibration testing signal. The results illustrated that LMD had an accurate reconstruction effect on the characteristic of blasting signal time and frequency，and it could reflect the complete information of original signal.Especially，compared with the Empirical Mode Decomposition（EMD），the LMD could apparently reduce the end effect of blasting vibration signal in the transformation，which improved the demodulation accuracy effectively.Meanwhile，analyzing the signal vibration energy distribution in frequency bands could further identify the characteristics of blasting to guide the blasting production preferably.

Blasting vibration；Explosion mechanics；Signal analysis；LMD；Energy

TD235.37

A

10.3969/j.issn.1006-7051.2016.05.004

1006-7051（2016）05-0018-06

2016-03-29

国家自然科学基金资助项目（51504129）

徐振洋（1982-），男，博士，副教授，从事爆破工程与岩石破碎的研究。E-mail：xuzhenyang10@foxmail.com