车门的位置和数量对地铁车辆车体扭转频率的影响*

李熙梦, 朱 涛, 肖守讷

(西南交通大学 牵引动力国家重点实验室, 四川成都 610031)



车门的位置和数量对地铁车辆车体扭转频率的影响*

李熙梦, 朱 涛, 肖守讷

(西南交通大学 牵引动力国家重点实验室, 四川成都 610031)

根据圆轴扭转频率计算公式，推导了基于车体关键设计参数的车体一阶扭转频率计算公式；建立了简化的车体钢结构有限元模型，分析了不同的车门位置和车门数量对车体扭转频率的影响，得到了车门对扭转刚度的影响规律；简化车体的一阶扭转频率计算结果与有限元计算结果进行对比表明，其误差在允许范围之内；最后，基于某实车模型，对车门的位置和数量对车体的扭转频率的影响进行了分析。研究结果表明：推导的简化车体一阶扭转频率计算公式简单有效；车门的位置离端墙越近车体的一阶扭转频率越小，在靠近中间位置扭转频率值达到最大，随着门的数量增加，一阶扭转频率会减小。

车体； 车门； 一阶扭转频率； 理论计算

机车车体的刚度特性具有举足轻重的作用，车体刚度的不合理将直接影响车体可靠性、安全性等关键指标[1]。刚度不足会引起较大的车体变形，导致车体振动频率降低，容易与车上设备产生共振，削弱连接接头的疲劳强度，从而降低车体的疲劳寿命，也会影响列车运行的安全性和舒适度[2]。同时，刚度不足还会使车门车窗出产生较大变形，影响车体的气密性。而刚度过大会从一定程度上增加车体的重量，恶化列车的运行工况，影响列车运行的安全性[3]。刚度过大还容易导致整体刚度过度不合理现象，如果有交变载荷作用于局部刚度过大的位置，那么该部位通常会产生局部集中现象，导致结构产生疲劳强度问题。因此，在车体结构设计与改进过程中进行刚度性能的分析具有重要的现实意义。车体刚度主要指整体弯曲刚度和整体扭转刚度[4]。本文主要针对扭转刚度进行研究，而车体扭转刚度的主要评价参数为扭转频率。

列车车门的设置位置和数量均会对列车的扭转刚度产生影响，目前我国的地铁列车被分为A、B、C 3种车型，根据客户的需求，其车门的位置和数量也有所不同。

本文推导了基于车体关键设计参数的车体一阶扭转频率计算公式，建立了简化的车体钢结构有限元模型，分析了不同的车门位置和不同的车门数量对车体扭转刚度频率的影响，得到了车门对扭转刚度的影响规律，并基于某实车模型，对车门的位置和数量对车体的扭转频率的影响进行了分析，为车体车门位置及数量的设计提供了理论和工程指导。

1 一阶扭转频率计算理论推导

1.1 圆轴及矩形截面梁扭转频率计算

对于车体的一阶扭转频率计算还没有明确的计算公式，本文在圆轴的扭转频率公式基础上推导出简单车体的一阶扭转频率计算公式。根据机械振动理论，图1(a)为圆轴的扭转振动示意图[5]。

图1 自由细长杆扭转振动频率原理

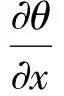
(1)

(2)

由图1(b)可得这一微元段的运动微分方程：

(3)

单位长度的转动惯量I(x)=I=常数，单位体积的质量ρ(x)=ρ=常数，极惯性矩Ip(x)=Ip=常数，且有I=ρIp，则式(3)可简化为

(4)

因为研究轴的自由振动的，则f(x,t)=0有

(5)

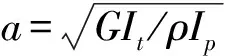
(6)

式中a为弹性波沿x轴的传播速度，描述圆轴扭转的角位移函数θ(x,t)的解为：

(7)

式中4个待定常数A,B,C,D决定于边界条件和初始条件。带入初始条件和边界条件可求得轴的无限多阶固有频率：

(8)

此频率为圆频率，而有限元算出的是自然频率，两者之间的关系为

(9)

所以圆轴的一阶扭转角频率为

(10)

对于圆轴有It=Ip，而对于矩形轴则不相等，而式中的It在算矩形截面梁时为梁截面的扭转常数J。

则矩形截面实心梁的一阶扭转频率计算采用式(11)。

(11)

在有限元中建立矩形截面梁，计算得到的一阶扭转频率结果与使用式(11)计算得到的一阶扭转频率结果对比，误差在10%以内，满足工程应用误差要求。证明式(11)对计算简单矩形截面梁的一阶扭转频率有效。

1.2 简化车体钢结构扭转频率的推导

计算车体的一阶扭转频率可以参照矩形截面梁的扭转频率公式，而车体有开门设置，出现断面，我们可以考虑将车体等效成许多段梁的串联, 分段如图2(a)所示，而每段梁对应一个长度，如图2(b)所示，在开门出现断面处，看成是上下两段梁并联，如图2(c)所示。

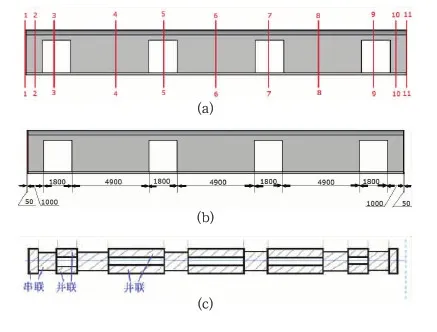
图2 车体的分段形式

参照弹簧悬挂频率公式:

(12)

将梁的一阶扭转频率公式等效成：

(13)

对于直径相等的等直轴来说，扭转刚度表示产生单位扭转所需要的扭矩[6]：

(14)

K为扭转刚度;M为扭矩;φ为扭转角;l为每段梁的长度。

如果实际轴端是由几个不同轴端串联成的，则整个轴端的扭转刚度的倒数(即为柔度)具有可加性，即

(15)

式中K1,K2，……，Kn表示各个串联轴端的扭转刚度。 将梁看成段串联的弹簧，则等效刚度

(16)

每段梁转动惯量为：

(17)

总转动惯量为每段梁的转动惯量相加:

(18)

当车体开门时，组成车体的各段梁形心不在同一坐标轴上，所以需将各自的极惯性矩等效到车体的扭转轴上，利用材料力学中的平行移轴公式[7]：

Iz=Izc+b2A

(19)

a、b分别为形心到扭转中心的位置，A为截面面积。带入计算公式后得到的简化车体一阶扭转频率计算公式(20)。

(20)

式中，Li为每段梁的长度，G为弹性模量，J为车体截面的扭转常数，a,b为截面质心到整体质心的位置，A为车体截面面积，ρ为车体材料的密度，Iyi,IZi为车体截面的惯性矩。

2 车门方案与有限元模型的建立

本文采用Hypermesh建立车体有限元模型，准确的有限元模型是仿真分析的关键，但如果完全按照车体的实际情况来建立模型，理论上虽然可以得到精确的计算结果，但是过分详细地追求车体结构的某些细节，势必会导致计算效率降低，因此首先建立了简化的车体模型，研究不同车门方案对车体一阶扭转频率的影响即可。

主要考虑车门对车体扭转刚度的影响， 依据深圳3号线车体模型为原型建立车体的简单模型。为了方便计算，所建立的模型计算时均用同一种材料，车体的基本参数如表1所示。

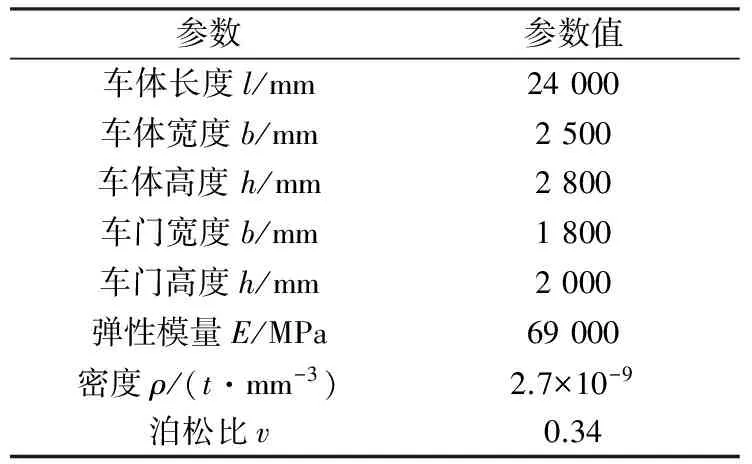
表1 车体所用材料参数

考虑车门位置对扭转刚度的影响时采用图3示例模型，示例模型中门的位置离一位端端墙为1 050 mm,然后依次向二位端移动1 000 mm，得到21个计算模型，在离一位端11 050 mm处开门时基本处于车体的中间位置。

图3 车体开1门示意图

当考虑门窗的数量时，参照目前地铁车的开门数量，分别取了开3门如图(4)所示，开4门如图(5)所示和开5门如图(6)所示的计算模型。

图4 车体开三门模型图

图5 车体开4门模型图

图6 车体开五门模型图

3 计算对比分析

3.1 车门位置对扭转刚度的影响

首先研究了车体开一门，但门开在不同位置的车体一阶扭转频率，计算结果如图7所示(由于篇幅限制，仅给出车门开在离一位端端墙距离1 050 mm的扭转图示)。

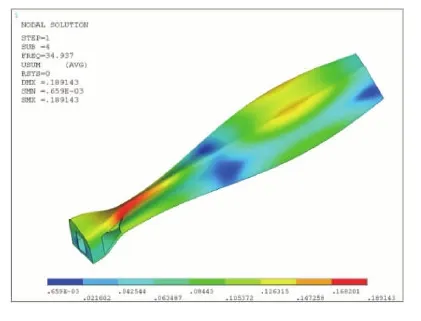
图7 车体开1门的一阶扭转模态

经过计算，得出了21个车门方案的车体一阶扭转频率的有限元计算结果，并且通过理论计算，得到其一阶扭转频率的理论计算结果，二者的计算结果如表2所示。

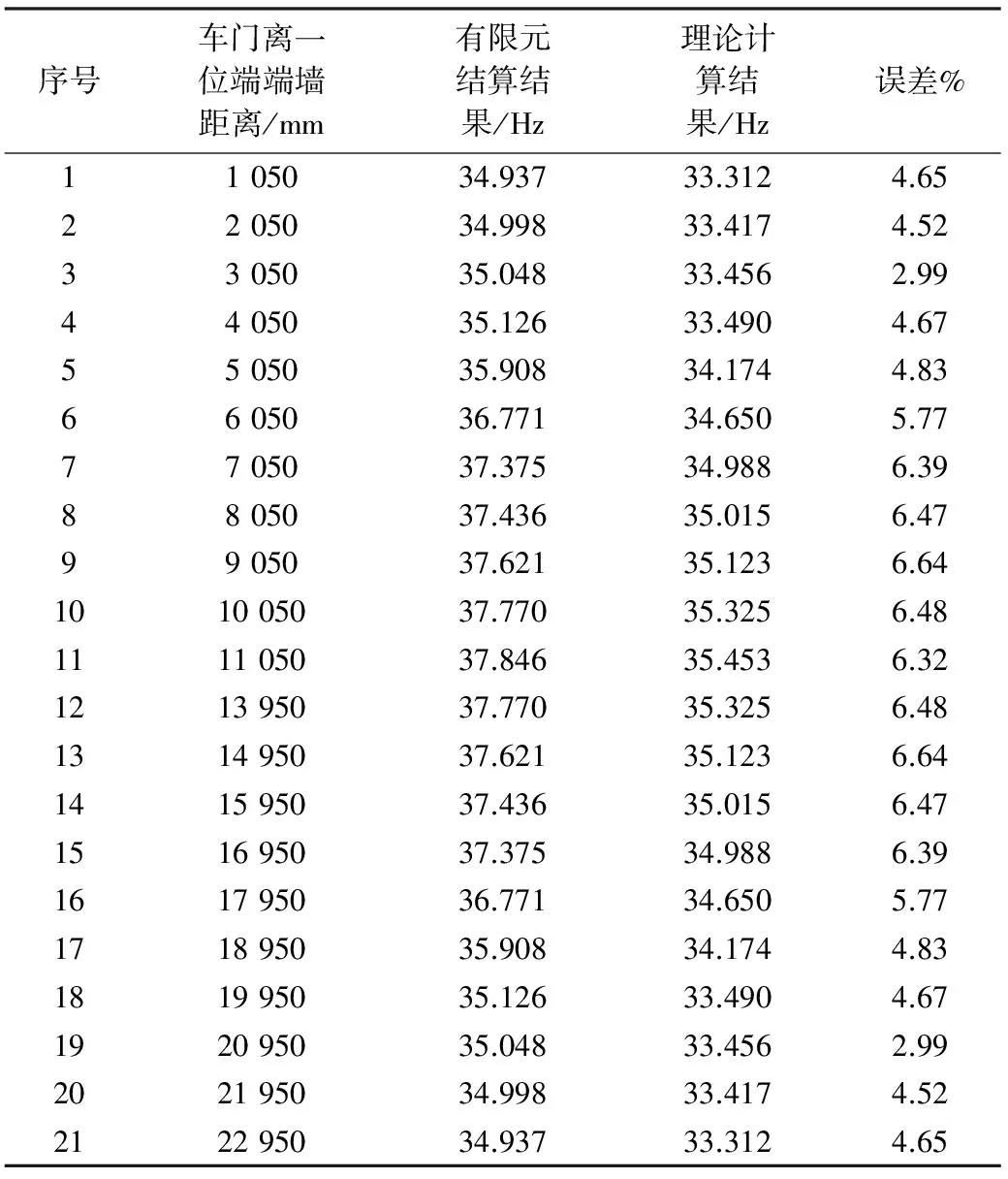
表2 一阶扭转频率计算结果对比

由表2中的有限元计算结果可以得出车门离一位端端墙不同位置与车体一阶扭转频率的关系，如图8所示。

由图表可以得知车门的位置离端墙越近则车体的一阶扭转频率值越小，车体扭转刚度也越小，在靠近中间位置扭转频率值达到最大，即车体扭转刚度达到最大。

由理论计算结果与有限元计算结果对比可知，公式(20)对计算简化车体的一阶扭转频率有效。

图8 开门位置与一阶扭转频率有限元结果的关系图

3.2 车门的数量对扭转刚度的影响

在ANSYS中计算出的开3门，开4门，开5门有限元计算结果和理论结果，如表3，各车体的一阶扭转频率，如图9～图11。

表3 开不同数量的车门的车体一阶扭转频率结果

图9 开3门的车体一阶扭转频率图

图10 开4门的车体一阶扭转频率图

图11 开5门的车体一阶扭转频率图

由得出的结果可知，随着门的数量增加，一阶扭转频率减小，即车体的扭转刚度减小。为了更进一步验证结果的正确性，在某地铁实车的基础上做开2门和开3门的实形一阶扭转频率分析。得到的车体一阶扭转频率的结果如表4，模态振型如图12和图13。

表4 开2门和3门的是实形车扭转频率计算结果

图12 开2门的实形车一阶扭转频率图

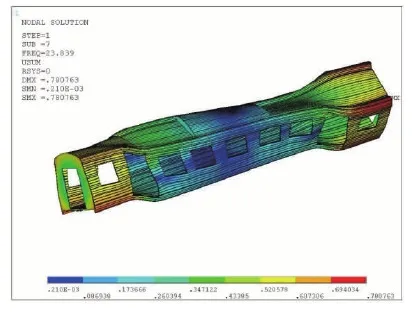
图13 开3门的实形车一阶扭转频率图

通过对实形车车体的计算更进一步验证了随着车门的数量增加，车体的扭转频率值减小，且通过基于实车的扭转频率计算，证明了在提取车体关键参数的前提下，公式(20)可以计算出可接受的频率结果。

4 结 论

根据圆轴扭转频率计算公式推导了基于车体关键设计参数的车体一阶扭转频率计算公式，建立了基于有限元ANSYS的简单车体有限元模型，计算得到了相同车体开一个车门且将车门开在不同位置下的一阶扭转频率，和相同车体分别开3,4,5个门情况下的一阶扭转频率，得到了车门对扭转刚度的影响规律。研究结果表明：

(1)车门的位置离端墙越近则车体的一阶扭转频率值越小，在靠近车体中间位置扭转频率值达到最大；

(2)车体上开不同数量的车门时，随着车门的数量增加，一阶扭转频率会随之减小；

(3)为了增大车体的扭转刚度，可以适当减小开车门的数量，若在车门数量较多时，车门可以适当向车体中心靠近，可以增大车体的扭转刚度。

(4)从振型图中可以看出：在开门位置，车体的扭转幅度较大，在车体设计时应该通过立柱，横梁等结构加强该位置的连接；

(5)简化车体的一阶扭转频率理论计算结果与有限元计算结果相对比，误差较小，表明公式(20)对计算简化的车体的扭转频率有效，复杂的车型可以在此基础上继续推导。

[1] 刘晓波.机车车体断面结构的优化设计[J].电力机车车辆与城轨车辆,2008,31(4)：27-30.

[2] 万 波.高速列车车体主要参数关系的研究[D].成都：西南交通大学,2012.

[3] 郭 鹏.底架承载式机车车体刚度性能研究[D].成都：西南交通大学,2015.

[4] 贺小龙.增加车门对列车车体垂弯动刚度的影响[J].噪声与振动控制,2014，34(2)：103-106.

[5] 张义民.机械振动[M].北京：清华大学出版社,2007

[6] 赵 征.基于ANSYS内燃机曲轴扭转刚度的研究[D].郑州：河南科技大学,2011.

[7] 孙训方.材料力学[M].北京：高等教育出版社,2002.Influence of the Location and Number of the Door to the Torsional Stiffness of the Subway Car-body

LIXimeng,ZHUTao,XIAOShoune

(Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031 Sichuan, China)

To study the impact of the position and the number of the door towards the first-order torsional frequency of the car-body steel structure, first of all, formula of the first-order torsional frequency of the car-body based on the key design parameters is deduced according to the circular shaft torsional frequency calculation formula；Secondly, simplified finite element model is established and the impact of the position and the number of the door towards the first-order torsional frequency of the car-body steel structure is analyzed. Based on the above analysis, the influence law of the door on the torsional rigidity is got; meanwhile, the result of deduced formula of the first-order torsional frequency is compared with the FE results. The error value is within the scope of the permit; at last, the impact of the position and the number of the door towards the first-order torsional frequency of the car-body steel structure is analyzed with a real vehicle model. The result shows that deduced formula of the first-order torsional frequency is simple and effective; the closer the door the end wall, the smaller of the first-order torsional frequency. When the door is at the middle of car-body the torsional frequency comes to biggest, and with the number of the door increasing the first-order torsional frequency will decrease.

car-body; door; first-order torsional frequency; theoretical calculation

*国家科技支撑计划项目(2015BAG12B01-15)；四川省科技厅应用基础研究项目(2014JY0242)。

��)女，硕士研究生(

2016-03-29)

1008-7842 (2016) 05-0064-05

U270.1 U239.5

A

10.3969/j.issn.1008-7842.2016.05.14