轮辋浅层裂纹伤损容限分析*

张澎湃

(中国铁道科学研究院 金属及化学研究所， 北京 100081)



轮辋浅层裂纹伤损容限分析*

张澎湃

(中国铁道科学研究院 金属及化学研究所， 北京 100081)

将“含与表面切线平行的圆片裂纹的半无限体表面承受滚压(含滑动)赫兹接触”问题应用于轮辋浅层埋藏型裂纹的损伤容限研究，提出了一种基于解析解的轮辋浅层裂纹应力强度因子计算方法。为解决既有应力强度因子塑性修正方法不适用于裂纹扩展寿命估算的问题，以降低应力强度因子为修正目标，提出一种新的塑性修正公式。在实测国产动车组D1车轮轮辋断裂力学性能指标基础上，综合应变能密度因子理论和上述应力强度因子计算方法、塑性修正公式开展了轮辋浅层裂纹起裂临界尺寸及伤损容限研究，通过类比分析了踏面类型、辐板形状对动车组车轮轮辋浅层裂纹扩展条件及伤损容限的影响规律。仿真结果表明：轮辋浅表裂纹扩展时以Ⅱ型裂纹扩展为主，基本上属于剪切应力作用的滑开型裂纹；在动车组轴重范围内，直径不大于1 mm的圆形面片裂纹对应的应力强度因子小于裂纹扩展门槛值，因此裂纹不会扩展，该研究成果可为探伤标准制定提供理论依据。

车轮； 轮辋浅层裂纹； 应力强度因子； 伤损容限

1 车轮轮辋伤损的研究现状

车轮轮辋伤损可分为浅表伤损和内部伤损，具体可细分为剥离、掉块、浅表裂纹、辋裂等运用故障，在《动车组车轮自主创新——阶段评审研究报告》中对动车组运行范围内的不完全统计表明：进口轮对发生的重点故障包括车轮辋裂3件、月牙形裂纹113件、踏面剥离件39件。这些运用数据表明，踏面剥离和月牙形裂纹发生概率比辋裂故障率高得多，该现象可以用图1解释。该图给出了Mises应力随轮辋深度的变化曲线，由图可知踏面表面至踏面下6 mm处对应的Mises应力数值较大，其中踏面表面至踏面下1 mm(LMA踏面除外)以及踏面下2 mm～4 mm对应Mises应力最大，假设制造缺陷在轮辋中均匀分布，轮辋浅层应力数值高，因此容易萌生裂纹，随着踏面深度增大，应力水平不断降低，裂纹萌生概率也随之减小。

上述故障属于不同深度裂纹源对应的轮辋裂纹扩展后的表现形式，均由轮轨滚动接触疲劳引起。当裂纹源深度小于5 mm时多形成浅表裂纹或踏面剥离，当裂纹源深度大于5 mm时裂纹一般会埋藏在轮辋内部。踏面旋修时发现的浅表裂纹一般定义为月牙形裂纹，与踏面剥离一样，发现月牙形裂纹的车轮也允许旋除裂纹后继续使用，但一般旋修量要达到3 mm～12 mm，造成车轮使用寿命大幅降低。

目前辋裂及踏面失效分析多基于裂纹断口分析，通过对断口形貌、低倍组织、显微组织、残余应力、化学成分、常规力学性能、扫描电镜以及夹杂物类别等方面进行分析和观察[1]，研究裂纹的起裂位置和开裂原因。但是这种分析方法不能预测裂纹扩展的历程和寿命，这也是车轮运用检修维护中的短板之一。

图1 Mises应力与踏面深度的关系

对这一问题，以线弹性断裂力学为理论基础，针对轮辋浅层裂纹开展裂纹扩展仿真及伤损容限研究，以期为车轮探伤周期、轮对检修、运用维护提供理论指导。

2 裂纹扩展分析的关键技术问题

在线弹性断裂力学中，对于任一种载荷模式，无论零部件的几何形状和载荷数值大小如何，只要应力强度因子数值相同，则裂纹尖端附近应力场、位移场分布相同。应力强度因子是线弹性断裂力学中的一个重要概念，它表征了裂纹尖端的变形程度和应力水平，是判断裂纹扩展趋势或者估算裂纹扩展寿命的参量，当裂纹尖端的应力强度因子超过裂纹扩展的门槛值时裂纹开始扩展[2]。以线弹性断裂力学为理论基础，可以开展轮辋裂纹扩展仿真及裂纹损伤容限研究，但需要解决"如何计算应力强度因子、如何处理复合型裂纹应力强度因子、裂纹寿命估算时如何修正韧塑性效应、以及如何获取轮辋材料断裂力学数据"等关键技术问题。

2.1 轮轨接触浅层裂纹应力强度因子

轮轨接触区域尺寸远小于车轮滚动圆半径，可以采用赫兹接触理论计算轮轨接触应力和估算接触疲劳寿命。借助相关研究成果将线弹性断裂力学和赫兹接触理论相结合，能够开展轮辋浅层埋藏型裂纹扩展规律的初步分析。考虑到赫兹接触理论的适用范围，当轮辋浅层埋藏型裂纹尺寸小于赫兹接触理论计算的接触斑时，可将车轮视为半无限体，采用“含与表面切线平行的圆片裂纹的半无限体表面承受滚压(含滑动)赫兹接触”的解析解[3]进行描述和分析。

如图2所示，圆形面片裂纹半径为a，圆形面片距表面的径向距离为d，接触区域接触斑半宽尺寸为c，接触斑中心距圆形面片圆心的距离为e，接触应力用p(x)描述，摩擦力引起的切应力用q(x)描述，具体计算公式为：

(1)

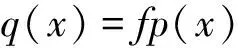
(2)

式中pmax为接触斑中心的接触应力，为接触斑中接触应力最大值。

图2所示圆形面片裂纹A点和B点的应力强度因子统一描述为：

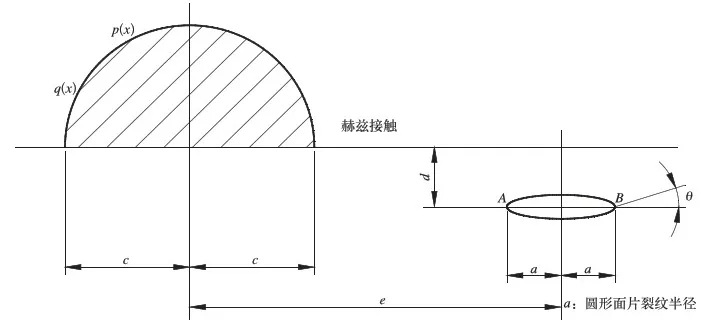
图2 轮轨接触区域与裂纹的相对位置

(3)

式(3)中的F1、F2取决于a/c，d/e，e/c和f；以a/c=0.48，d/c=0.48对应情况为例，给出不同f以及不同的e/c对应的A点和B点的F1、F2分布情况，具体见图3和图4。

2.2 复合型裂纹应力强度因子

轮辋内部缺陷所在位置在往复的轮轨接触应力作用下萌生裂纹并不断扩展，裂纹在产生拉伸变形的同时可能产生剪切变形扭转变形，因此裂纹可能同时承受3类裂纹形变的共同作用，即轮辋浅表层裂纹类型属于复合型裂纹。

为应用I型、II型、III型裂纹的断裂判据，需要计算复合型裂纹对应的等效应力强度因子Ke，计算等效应力强度因子Ke时需要解释扩展条件和扩展方向等两个问题：

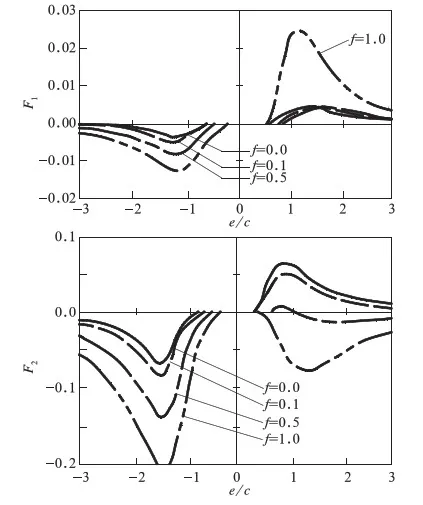
图3 A点处F1和F2系数

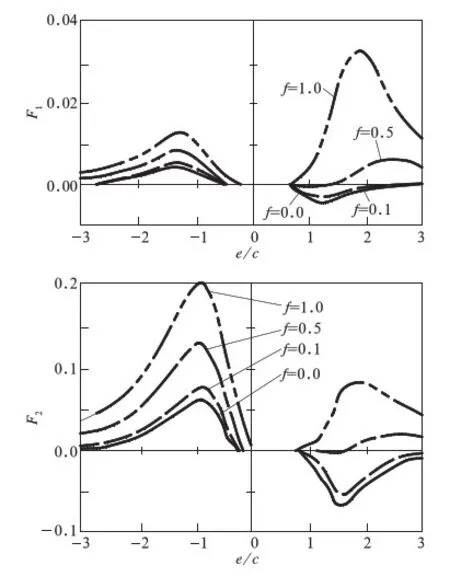
图4 B点处F1和F2系数

①扩展条件：当应力-应变场满足什么条件时，裂纹发生扩展；

②扩展方向：裂纹发生扩展的方向与应力-应变场的关系。

复合型裂纹对应的等效应力强度因子理论是在关于裂纹扩展方向(裂纹扩展角)和扩展条件的推断后，并通过试验证明后形成的观点，工程上取得理论主要有应变能密度因子理论、能量释放率理论和最大正应力准则等[4-6]。选用应变能密度因子理论分析复合型裂纹扩展问题。应变能密度渐进项展开式第一项S的表达式为：

(4)

式中：

(1+cosθ)-(3cosθ-1)]

其中，θ为角度;G为剪切模量;G=E/[2*(1+v)];E为弹性模量；v为泊松比；k为应力状态参量。可根据应力状态进行计算其数值，对于平面应变问题或者轴对称问题，k=3-4v；对于平面应力问题，k=(3-v)/(1+v)。

应变能密度因子理论认为应变能密度因子的最小值Smin达到临界值时裂纹开始扩展，扩展方向为确定Smin时的角度 ，应变能密度因子理论可以采用式(5)所示的方法计算复合型裂纹对应的等效应力强度因子。

(5)

应用数值计算方法计算式(4)中S的最小值Smin，同时获得Smin对应的扩展角 ，进而获得等效应力强度因子 。

考虑到应力强度因子K1为负值时，I型裂纹处于闭合状态，不会产生扩展，故对于式(5)而言，若K1为负值，则令K1=0并重新计算Smin和等效应力强度因子Ke。

2.3 应力强度因子的塑性修正方法

线弹性断裂力学认为结构为线弹性体，忽略了裂纹尖端的塑性变形以及由此引起的应力松弛，为获得接近真实情况的评判结论，需要对应力强度因子进行必要的塑性修正。

经典的Irwin塑性修正方法[7]见式(6)，该修正公式该方法采用等效裂纹长度 处理塑性应力松弛，公式增大了应力强度因子的数值，进而提高了裂纹扩展驱动力，这与增强塑性来提高韧性的原理相矛盾，为弥补这一缺陷，Irwin塑性修正方法需要按照同样的修正方法对裂纹扩展阻力进行修正，断裂韧性 的修正公式为式(7)。

(6)

(7)

式(6)和式(7)的修正工作能够解释塑性对韧性的增强作用，但在工程应用中仍存在无法解决的问题：对于亚临界扩展过程的寿命估算而言，当裂纹尺寸不满足小范围屈服条件时，若不进行塑性修正，仅采用线弹性断裂力学的应力强度因子进行估算将得到较保守的寿命估算值，式(6)所示的修正方法增大了应力强度因子数值，若用于寿命估算，将会得到过于保守的结果。

式(6)和式(7)的修正工作能够解释塑性对韧性的增强作用，但在工程应用中仍存在无法解决的问题：对于亚临界扩展过程的寿命估算而言，当裂纹尺寸不满足小范围屈服条件时，若不进行塑性修正，仅采用线弹性断裂力学的应力强度因子进行估算将得到较保守的寿命估算值，式(6)所示的修正方法增大了应力强度因子数值，若用于寿命估算，将会得到过于保守的结果。

为解决上述修正方法带来的这些问题，认为裂纹尖端塑性区导致的应力松弛降低了裂纹尖端的应力水平，从而降低了应力强度因子的数值，进而降低裂纹扩展驱动力，同时提高了韧性和裂纹扩展阻力，这与通过增强塑性来提高韧性的原理相一致。基于上述观点，借助等效裂纹长度概念，从降低应力强度因子的角度出发进行修正并获得一个新的应力强度因子的塑性修正方法。受篇幅所限，不再对修正理论和修正过程进行叙述，仅给出最终推导获得的修正公式，见式(7)～式(9)。

(7)

(8)

(9)

式(7)～式(9)中，r0为裂纹线上弹性区与塑性区分界点到裂纹尖端的距离，a为裂纹长度。

式(7)～式(9)所示塑性修正方法假设裂纹耦合面间相对变形为线性，未考虑裂尖区域非线性因素影响，因此存在一定修正误差。然而上述公式能够直接解释塑性对韧性的增强作用，同时可直接用于基于线弹性断裂力学的亚临界扩展过程的寿命估算，也能够解释断裂力学小范围屈服条件，具有一定的物理意义。

2.4 国产动车组D1车轮轮辋材料断裂力学数据

关于疲劳裂纹扩展速率的测量方法较为成熟，如GB/T 6398-2000中规定的测量方法[8]。Paris公式参数最为简单，应用较为广泛，它能够较好的描述裂纹扩展的第II阶段。本次采用Paris公式描述裂纹扩展速率，当线性相关系数R为0.941时，试验结果如式(10)所示。

(10)

考虑到材料微观结构差异、试样几何尺寸差异、实验加载误差、裂纹长度测量误差以及ΔK计算误差均会造成ΔK-da/dN曲线分散性，因此不宜直接采用降ΔK方式测试疲劳裂纹起裂门槛值ΔKth，引入Hartman公式描述缓慢扩展阶段I的裂纹扩展行为：

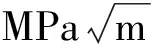
da/dN=6.4662×

(11)

3 轮辋浅层裂纹损伤容限分析

3.1 踏面类型、辐板结构对应力强度因子的影响

车轮踏面廓形、轮对横移量和车轮辐板形状对轮轨接触应力有一定程度影响，与标准60轨在平衡位置接触时，轮轨Mises应力、轮轨接触应力、接触斑尺寸与轮轨踏面廓形、轮型的对应关系见表1。

表1 轮轨接触应力、接触尺寸与车轮踏面、轮型的关系

由式(10)可知应力强度因子的变化范围决定裂纹扩展速度，故需要考虑应力强度因子的最大值和最小值两种情况，车轮转动过程载荷作用位置变化引起的应力强度因子变化范围可用应力强度因子的最大值与最小值之差描述。为计算图2中A点和B点对应的应力强度因子K1和K2的最大值和最小值，首先根据图3和图4确定F1、F2的最大值和最小值，再应用式(2)、式(3)计算应力强度因子的最大值和最小值。

车辆运行时轮轨间处于滚动摩擦状态，其摩擦系数小于滑动摩擦，根据经验，设轮轨间滚动摩擦系数f=0.1。图5给出不同半径圆形面片裂纹对应的应力强度因子变化范围ΔK1、ΔK2。由图5可知，轮辋浅表裂纹扩展时以II型裂纹扩展为主，且K2比K1大一个数量级以上，说明轮辋裂纹扩展基本上属于剪切应力作用的滑开型。

图5 不同踏面和轮型对应的应力强度因子变化范围ΔK1、ΔK2

当钢轨廓型为标准60轨时，不同的裂纹长度下，CRH3-CN对应的应力强度因子数值最小，而CRH5-XP55对应的应力强度因子数值最大，CRH1-LMA对应的数值介于CRH3-CN和CRH5-XP55之间。计算数据也表明，当钢轨廓型和车轮踏面固定时，改变辐板结构形状也会影响应力强度因子，若钢轨和车轮踏面分别采用标准60轨和LMA踏面时，HFS车轮对应的应力强度因子小于CRH1、CRH2、CRH5等轮型，可见适当降低车轮辐板径向刚度对提高轮轨接触强度有一定程度促进作用。

3.2 缺陷不起裂的临界直径

应用应变能密度因子理论计算等效应力强度因子Ke和扩展角θe，解析解中裂纹为形状规则圆形面片，受该理论假设影响，上述各种条件下计算获得θe均为85.2°，等效应力强度因子计算值见图6。

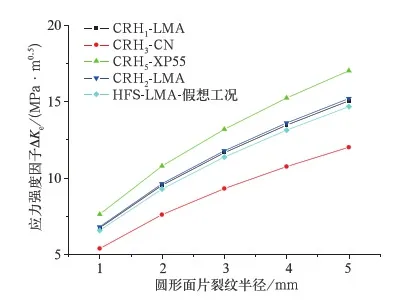
图6 不基于应变能密度因子理论的等效应力强度因子

对图6所示曲线进行拟合，可得与标准60轨配合，且轮轨间滚动摩擦系数f=0.1时踏面浅表区域对应的线弹性断裂力学信息，见表2。

表2 不同踏面对应的线弹性断裂力学信息

我国动车组车轮自主创新项目中制定的《200～250公里时速动车组用辗钢整体车轮试制技术条件》规定轮辋超声波探伤时轮辋内部不得有大于等于φ1 mm平底孔当量缺陷；透声性能要求在轴向检验时，回波衰减不应高于4 dB。由表2可知，对于我国既有时速不大于250 km的动车组车轮而言，该试制技术条件对轮辋缺陷的规定是合理的，但对XP55踏面而言，轮辋内部缺陷的尺寸裕量最小。

3.3 损伤容限及剩余寿命

以统一形式描述表2中等效应力强度因子拟合式为

(12)

式(12)中的C1和C2数值可由表2查询获得。

假设轮辋浅表裂纹扩展形态为圆形面片，且不考虑裂纹扩展角度，则结合式(11)、式(12)得

da/dN=6.4662×10-7×

(13)

对式(13)进行公式变换，得

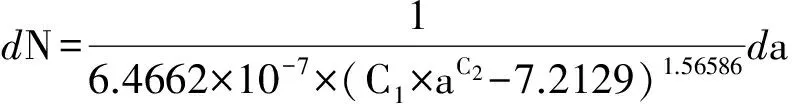
a≥d0/2

(14)

结合式(14)和表2，应用勒让德-高斯求积法[9]求解裂纹半径从d0/2扩展至5 mm对应的扩展寿命，计算结果见表3。

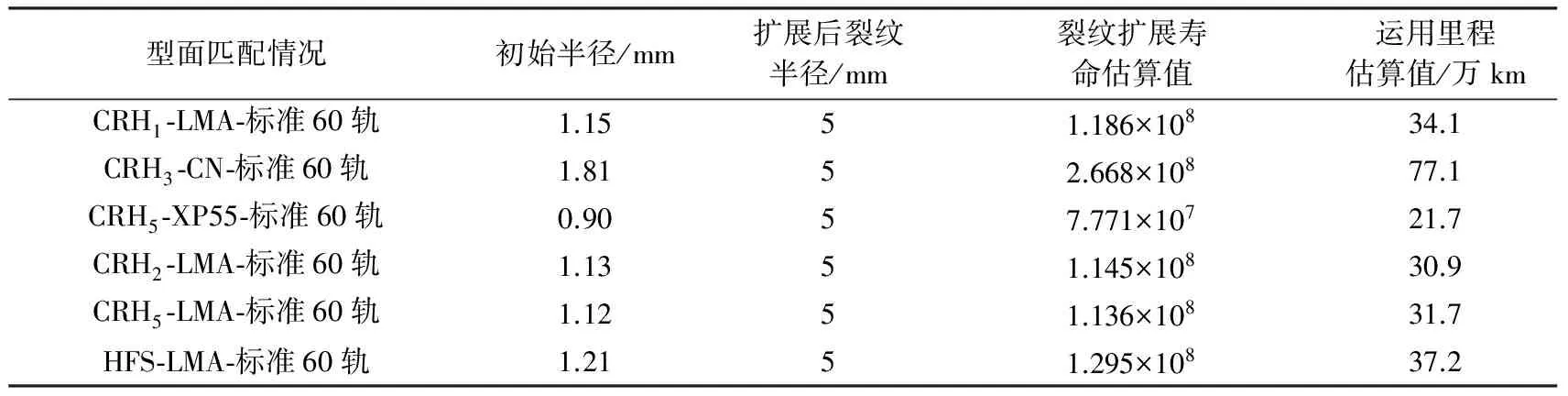
表3 不同踏面对应的裂纹扩展性能估算值

由表3可知，踏面型面和轮型对裂纹起裂临界尺寸、裂纹扩展寿命均有影响，其中踏面型面的影响最为显著，选用低接触应力踏面可有效提高抗裂纹扩展的能力并显著延长裂纹扩展寿命。从另外一个角度看，在同样的运用条件下，选用低接触应力踏面可以适当放宽对车轮轮辋内部缺陷尺寸的要求，这对于降低车轮产品成本优化车轮生产工艺流程、减少车轮产品废品率等具有工程参考意义。

4 结 论

(1)通过测试D1材质动车组车轮轮辋部位断裂力学参数，获得轮辋材料Paris公式、Hartman公式及裂纹扩展门槛值；这些数据可为轮辋损伤容限研究提供基础数据支持；

(2)轮辋浅表裂纹扩展时K2比K1大一个数量级以上，裂纹以II型剪切扩展为主，基本上属于剪切应力作用下的滑开型裂纹；

(3)在动车组轴重范围内，与轮轨接触区切向平行的圆形面片裂纹，若其直径不大于1 mm，其应力强度因子小于裂纹扩展门槛值，因此裂纹不会扩展，该结论可为探伤标准的制定提供理论依据；(4)踏面型面和辐板形状对轮轨接触应力、裂纹起裂临界尺寸、裂纹扩展寿命均有影响，其中踏面型面的影响最为显著，动车组车轮设计时，在合理选取踏面廓型前提下尽量降低车轮径向刚度，可以达到良好的设计效果，对于运用维护、检修等也具有积极意义。

[1] 付秀琴，张 弘，丛 韬. DF11机车车轮轮辋裂纹分析报告[R]. 北京：中国铁道科学研究院，2013.

[2] Williams J G， Ewing P D. Fracture under Complex Stress-The Angled Crack Problem [J]. International Journal of Fracture Mechanics， 1972，8(4):441-446.

[3] 中国航天研究院. 应力强度因子手册[M](增订版). 北京：科学出版社，1993.

[4] 郦正能 张纪奎. 工程断裂力学[M]. 北京：北京航空航天大学出版社，2012.

[5] 赵建生. 断裂力学及断裂物理[M]. 武汉：华中科技大学出版社，2006.

[6] 张晓敏,万 玲,严 波,等. 断裂力学[M]. 北京：清华大学出版社，2012.

[7] Irwin G R. Analysis of stresses and strains near the end of a crack traversing a plate [J]. J. Appl. Mech. ，Trans.， ASME，1957，24(3):361-364.

[8] GB/T 6398-2000 《金属材料疲劳裂纹扩展速率试验方法》[S].

[9] 徐士良. Fortran常用算法程序集[M](第二版).北京：清华大学出版社，1995.Damage Tolerance Analysis of Shallow Internal Crack of Rim

ZHANGPengpai

(Metals and Chemistry Research Institute, China Academy of Railway Sciences, Beijing 100081, China)

"Surface contact problem (including sliding) of semi-infinite body with internal circular patch crack which is parallel to the tangent surface" is applied to simulation of shallow internal crack of rim. And a calculation method of stress intensity factor basing on analytical solution is put forward here. In order to solve the problem which the existing plastic correction method of stress intensity factor is not applicable to life estimation of crack propagation, taking reducing stress intensity factor as target revision, a new kind of plastic correction method of stress intensity factor is obtained by formula derivation. On the basis of testing fracture mechanics parameter of wheel rim of D1 material, comprehensive strain energy density factor theory, calculation method of stress intensity factor above and plastic correction method, this paper carried the research of critical dimension and damage tolerance for rim's shallow internal crack. The influence law of crack propagation conditions and damage tolerance for rim shallow internal crack of EMU wheel under factor of tread type and wheel web has been analyzed by analogy analysis. The simulation results show that crack of Ⅱ type dominates rim's crack process, so rim crack mainly belongs to slide open type crack under shear stress. The circular patch crack will not grow if its diameter is less than 1mm because the stress intensity factor is less than the crack propagation threshold within the range of EMU axle load. The results can provide theoretical support for making Inspection standard.

wheel; shallow internal crack of rim; stress intensity factor; damage tolerance

*高铁联合基金重点项目(U1234207)；国家重点基础研究发展计划项目(2015CB654800)；中国铁路总公司科技研究开发计划课题(2015J003-E，2015J007-E，2014J004-I，2013J008-C)； 国家“863”计划资助项目(2015AA034302)

��)男，工程师(

2016-03-29)

综合技术研究

1008-7842 (2016) 05-0001-06

U211.5

A

10.3969/j.issn.1008-7842.2016.05.01