动态需求下的损耗品生产—零售库存优化

伏开放，陈志祥

动态需求下的损耗品生产—零售库存优化

伏开放，陈志祥

（中山大学管理学院，广州510275）

研究一类需求与库存相关的动态需求下损耗品生产—零售库存优化问题。针对分散决策低效率问题，建立数量折扣契约，使得制造商与零售商在各自独立决策时获得集中决策时的优势。引入某连锁蛋糕店的销售数据，进行模型的应用。结果表明：当生产成本过高时，制造商发生亏损；当零售价格过低时，零售商减少订货量导致制造商发生亏损；单位存储费越高，双方利润越低；当订货费或生产准备费增加时，制造商与零售商呈现相反的利润变化趋势；双方均对反映动态需求率的规模参数与形状参数变化敏感，但对形状参数的变化更敏感；采用的数量折扣契约可以协调生产—零售库存系统，但由于话语权的不同，制造商依然获得协调后的大部分利润。

动态需求；损耗品；分散决策；集中决策；数量折扣

由于库存的选择效应和广告效应，市场上存在这样的产品，产品在货架上摆放的数量越多，需求越旺盛，如农贸市场中果蔬、生鲜、肉类、面包、奶制品等产品，此类产品的需求均表现出与库存相关的特点，需求随库存的变化而动态变化。同时，此类产品由于腐蚀、挤压、顾客拣选等原因导致产品损坏、变质。损耗产品失去价值退出市场，给商家造成损失，浪费大量资源，每年中国损耗的蔬菜与水果的价值高达89亿美元，约占全年产出的30％[1]。损耗带来的损失已不容忽视。易损耗品的稳定供给、供需平衡成为变质产品流通环节中迫切需要解决的问题。因此，合理的控制需求与库存相关的变质产品的订购量对于增加商家利润和社会福利及节约社会资源具有重要意义。

一、文献综述

产品的需求受多种因素的影响，例如，价格、质量、服务、时间等因素，本文所研究的动态需求主要指需求随库存水平变化而动态变化的需求，因此仅对关于需求与库存相关的研究进行综述。Dye等（2005）[2]假设需求是依赖于库存水平的线性函数，探讨了部分延期供给对最优策略的影响。Giri等（1998）[3]研究了依赖于时间与依赖于库存水平的非线性存储成本对库存补给策略的影响。Krommyda等（2015）[4]研究了可替代需求与库存相关的产品订购策略。Yang（2014）[5]在假设存储成本依赖于库存水平的基础上，探讨了需求依赖于库存水平的订购策略。Dye和Hsieh（2011）[6]在库存容量限制条件下，探讨了需求同时依赖于价格与库存水平的订购策略。

关于损耗品的库存模型，Chen（2013）[7]假设损耗率服从韦伯分布，运用泰勒级数展开的方法得出订购量的解析表达式，用模拟退火算法、粒子群优化算法、量子行为的粒子群优化算法对多目标约束下的利润函数进行了求解。Ouyang等（2006）[8]和Chang等（2015）[9]在给定延期支付策略条件下建立了时滞损耗产品的库存模型，并得到最优的订购策略。Arcelus等（2003）[10]研究了临时折扣策略对损耗品库存的影响。Maihami和Karimi（2014）[11]在随机需求及促销努力条件下建立了损耗品的库存模型并得到了最优的定价及补货策略。Hwang（1997）[12]构建了损耗率服从Weibull分布的EOQ模型。Cheng等（2011）[13]构建了梯形需求下损耗品的库存模型并得到最优补货策略。Das等（2014）[14]研究了损耗率服从韦伯分布，延迟支付条件下，需求依赖于广告和零售价格的集成库存决策模型，该库存模型假设供应商对零售商的供应有限的，并探讨延迟支付对供应商与零售商的相互影响。徐贤浩等（2007）[15]将需求视为是依赖于时间的时变需求，忽略物理变质，考虑无形变质，假设无形变质率与需求率成反比，比较分析了3种库存生产控制模型。

也有诸多学者在研究库存模型时同时考虑需求依赖于库存水平及产品的损耗过程。Chang等（2010）[16]研究证实，当需求依赖于库存水平时，易损耗产品库存系统会维持一个较低的水平，从而大大降低存储成本。Teng等（2005）[17]构建了损耗率为常数，需求依赖于库存水平的库存系统不允许缺货的EOQ模型。Wu等（2006）[18]在需求依赖于库存水平及延期供给条件下，得到了时滞变质产品的补货策略。Hou（2006）[19]在假设需求依赖于库存水平，损耗率服从常数的基础上，分析了资金的时间成本对订购策略的影响。国内学者对需求依赖于库存水平的损耗品的库存模型也做了深入研究。段永瑞等（2013）[20]基于不同顾客群体面对缺货时的等待意愿，指出当需求依赖于库存水平时，利润最大化问题不能简化为成本最小化问题，证明了最优解的存在性和唯一性，并运用牛顿迭代法进行了求解。黄卫来等（2007）[21]在考虑资金时间价值的基础上，假设需求为库存水平的线性函数，建立了最优订货批量模型。

生产—零售库存系统中各成员出于自身利益的考虑，做出使自身利益最大化的决策，而该决策往往与整体利益冲突，给生产—零售库存系统的优化带来困难，因此设计合适的契约机制来优化生产—库存成为研究的热点，其中就包括数量折扣契约机制。在供应链环境下，Saha等（2015）[22]在研究需求依赖于库存水平和价格的二级供应链的协调问题时，建立了零售价折扣契约、联合零售价折扣契约、批发价折扣契约和成本分担契约，通过比较各类契约下制造商与零售商的收益情况，发现虽然各类契约可以协调供应链，但不同库存弹性指数范围内，制造商与零售商对契约的偏爱并不总是一致。Partha等（2014）[23]将数量折扣契约与收益分享契约集成为组合契约，在该契约下研究了需求依赖于价格和库存水平的短生命周期产品的两层供应链协调问题。Mirzaee等（2012）[24]研究了一个由制造商和两个竞争零售商组成的两层生产—库存优化问题，零售商面临的需求依赖于广告投入量及竞争对手对广告的投入，通过采用由数量折扣契约和广告成本分担契约组成的联合契约实现生产—零售库存的优化。国内学者陈军等（2009）[25]针对生鲜产品的损耗，研究了生鲜品订购与协调问题。Zhou等（2008）[26]利用利润分享契约和数量折扣契约研究了需求依赖于库存水平的两层生产—库存优化问题，但没有考略产品的损耗过程。

上述文献关于需求与库存相关的研究往往针对供应链单一节点，大多不与供应链环节中的其他节点结合；关于损耗品的最优库存补货策略，多数从损耗率本身的性质出发考虑单一利益主体，同时研究需求与库存水平相关的损耗品的协调问题的较少。在多数应用数量折扣契约的供应链协调的文献中假设需求是随机变量，而假设需求是依赖于库存水平的较少，假设产品在销售过程中发生损耗的就更少。文章探讨需求与库存相关的动态需求下的损耗品在常数损耗率下的生产—零售库存优化问题，应用数量折扣契约，使得制造商与零售商在各自独立决策时获得集中决策时的优势，从而实现需求与库存相关的变损耗品的生产—零售库存的优化。文章的研究丰富了生产—库存优化理论，同时具有重要的现实意义。

二、模型描述、模型假设与变量说明

（一）模型描述

生产—零售库存系统由单个制造商与单个零售商构成，图1反映了系统中制造商与零售商的库存变化。制造商快速生产一类短生命周期易损耗品（例如：蛋糕），并迅速补给零售商。零售商将制造商所运送的所有产品展示销售。零售商面临的需求是动态变化的，动态需求率依赖于展示的产品数量。

（二）模型假设与变量说明

本文模型的建立基于如下假设。

1.生产—零售库存系统单个制造商与单个零售商构成；

2.制造商按订单生产，生产量等于订单量；

3.制造商与零售商之间的空间距离很近，忽略制造商的运输时间，因此不考虑运输成本；

4.制造商的生产时间极短，不考虑制造商的库存成本；

5.产品在制造商处不发生损耗，在零售商处发生损耗，已经损耗的产品无残值，损耗率θ为常数；

6.生产—零售库存系统不允许缺货；

7.零售商将所有产品放在柜台展示销售，动态需求率依赖于当前库存水平I（t），即D（t）=αI（t）β，α>0，0＜β＜1，α为不受零售库存影响的规模参数，β为库存形状参数。

8.制造商与零售商之间的博弈为Stackelberg博弈，制造商为Stackelberg博弈的领导者，零售商为Stackelberg博弈的跟随者。

本文模型中用到的参数和变量定义如下。

c为制造商单位产品生产成本（元）；w为制造商将产品批发给零售商的批发价（元）；p为零售商单位产品零售价格（元），满足c＜w＜p；θ为损耗率；T为一个订货周期（天）；Q为零售商期初订购量（单位）；为集中决策下生产—零售库存系统的最优订购量；为零售商分散决策下最优订购量（单位）；w*为分散决策下制造商制定的最优批发价（元）；Ar为零售商每次订购费（元）；Am为制造商每次生产准备费（元）；Ch为单位产品单位时间存储费（元/单位）；Cd为单位变质成本（元/单位）；γ为最优订购数量的倍数；δ为数量折扣因子；ø为零售商利润增加百分比。

三、集中决策下的生产-零售库存模型

依据假设条件，零售商库存水平变化的状态方程为

式（1）是一个伯努利方程，根据伯努利方程的求解公式及边界条件I（0）=Q有

由于e-（1-β）θt的非线性，对e-（1-β）θt进行泰勒级数展开，忽略二阶及二阶以上条件，有e-（1-β）θt=1-θ（1-β）t，则零售商随库存模型变为

由式（3），令I（T）=0，知零售商的订货周期为

零售商一个周期内的累计存储量

零售商一个周期内的累计销售量为

集中决策下，制造商与零售商视为一个联盟，从生产—零售库存系统的整体利益出发，做出使生产—零售库存系统整体利益最大化的库存决策，集中决策下生产—零售库存系统平均利润函数为

将式（4）～式（6）代入式（7）可得

命题1.集中决策下生产—零售库存系统的平均利润Πc（Q）是Q的凹函数，当pθ（1-β）-cθ（2-β）-Ch＜0时，存在唯一的使得Πc（Q）最大。

证明：对利润函数Πc（Q）分别求一阶导数与二阶导数，有

因为0＜β＜1，所以β-2＜0，在Q∈[0，∞）内d2Πc（Q）/dQ2＜0，故集中决策下生产—零售库存系统的平均利润Πc（Q）是关于Q的凹函数，dΠc（Q）/dQ是关于Q的严格递减函数。

所以集中决策下生产—零售库存系统的平均利润Πc（Q）是Q的凹函数，pθ（1-β）-cθ（2-β）-Ch＜0，存在唯一的使得Πc（Q）最大。证毕。

四、分散决策下的生产—零售库存模型

分散决策下，零售商与制造商之间的订货决策是一个Stackelberg博弈，制造商是Stackelberg博弈的领导者，零售商是跟随者，制造商先决策批发价w，零售商后决策订购数量Qr，采用逆向递归求解法求解子博弈精炼纳什均衡，也即先求最优订购量再求批发价w*。

分散决策下，零售商以自身平均利润最大化为决策目标，此时零售商的平均利润函数为

参照命题1的证明过程，易得d2Πr（Q）/dQ2＜0， Πr（Q）是Q的凹函数，存在唯一的使得Πr（Q）达到最大。满足dΠr（Q）/dQ=0，也即

制造商的平均利润函数为

分散决策下，制造商作为Stackelberg博弈的领导者，决定最优的w*来最大化自身的平均利润Πm（w）。

命题2.分散决策下，制造商利润Πm（w）是w的凹函数，存在唯一的w=w*使得Πm（w）最大。

证明：由（12）式知

根据隐函数的求导法则，有

其中

将w*代入式（12），可得由w*=M/N得w*，进一步可得

命题3.由于双边际化效应的存在，集中决策下的订购量大于分散决策下的订购量，即集中决策下的利润大于分散决策下生产—零售库存系统的利润，即

证明：由式（9）知

令h1（Q）＝αβ（p-c）Q+α（1-β）（Ar+Am）。

五、基于数量折扣契约的生产—零售库存优化

由命题3知，双边际化效应的存在，使得零售商订购量小于集中决策下的订购量，降低了生产—零售库存系统的效率，导致了社会福利的损失。通过制定激励措施，协调生产—零售库存系统内成员之间的关系，使协调之后的各方的利润之后达到集中决策时的水平，即使不能完全实现集中决策时的利润水平也可实现帕累托改进，增加各方收益。数量折扣就是一种有效的激励措施，有效的数量折扣契约通过降低价格、增加销售量，达到减少交易成本、降低市场风险、提高顾客满意度、实现各方“共赢”的目的。

通过建立需求与库存相关的易损耗产品的数量折扣契约，达到优化零售商库存的目的，实现分散决策下获得集中决策下的优势。制造商向零售商承诺，若零售商订购量不小于的γ倍，则批发价为w*的δ；若零售商订购量小于的γ倍，则批发价仍为w*。当分散情况下与集中决策时订购量相等时实现生产—零售库存系统的完美优化，此时也即

命题4.数量折扣契约的实施，折扣因子δ须满足如下条件

证明：分散决策下制造商与零售商接受该契约需满足的条件是

得折扣因子下限

得折扣因子上限

折扣因子δ存在下限，表明制造商提供的折扣因子不可能无限小，是为了保证制造自身利益；折扣因子δ存在上限，表明折扣因子不可能无限大，是为了维护零售商的利益。只要在上述区间内，双方就会接受契约，从而达到协调库存的目的。

现实中强势零售商（如7-11、苏果便利店、沃尔玛等）的话语权越来越强。在制定契约时会要求在原有利润的基础上百分比至少增加ø才会接受契约。

命题5.折扣因子δ须满足如下条件：数量折扣契约下，零售商最优平均利润为制造商的最优平均利润为最优折扣因子δ*为

证明:制造商作为Stackelberg博弈的领导者，在制定契约时，会使零售商获得接受该契约的最小收益，也即实行数量折扣契约后，供应链系统达到集成决策时的利润制造商的最优平均利润为也即

化简可得δ*。证毕。

六、数值仿真与敏感性分析

以上建立了生产-零售库存系统的数量分析模型，接下来以某连锁蛋糕店销售蛋糕产品为例，分析各参数变化对生产-零售库存系统利益双方利润变化的影响。

（一）基础数据

根据经验和以往销售数据，零售价格p=12元/单位，制造商的生产成本为c=8元/单位，零售商每次订购费Ar=20元，制造商每次生产准备费Am= 260元（生产准备费用包括生产设备的清洗和工艺更换，假设生产准备时间为1天，需要人工3人，每人每天工资是60元，另加各种辅助费用80元，合计260元），零售商放在冷柜中存储蛋糕产品，每天每单位的存储费为Ch=0.5元/天，因变质的蛋糕不能再销售也无法回收利用，在集中决策下，变质成本为生产成本，即Cd=8元/瓶，分散决策下的变质成本为批发价格。对历史数据分析，消费者对蛋糕的动态需求率近似为D（t）=30I（t）0.4，从而有α＝30，β＝0.4，蛋糕在存储过程中的损耗率为θ＝0.05。

必须说明的是，因为许多成本数据对于企业来说，是商业保密的数据，因此，考虑这样的情况，本文的成本数据并不是真实的数据，是一个估算的数据，但是不失一般性，我们只是用来模拟决策分析过程。

（二）决策分析

利用Matlab 7.0进行求解，得出集中决策下，订购数量为单位，整体利润分散情况下制造商基于自身利益最大化，给予零售商的批发价为w*=9.94元/单位，零售商每次订购量为瓶，零售商利润为元，制造商的利润为元，在分散决策情况下，生产-零售库存系统的渠道效率为整个奶制品供应链系统存在的效率损失。

通过建立数量折扣契约，零售商在自身利润增加的情况下，即ø=30。如果零售商订购量不小于2 264单位，即订购量不小于分散决情况下的4.205 7倍（γ=4.205 7），制造商就在原有批发价的基础上给予零售商0.930 06的折扣（δ*=0.930 06）。优化之后，零售商的利润为340.41元，制造商的利润为522.33元，增加50.43％。双方协调之后利润均有所增加，但奶制品制造商的利润增加比例超过零售商，牢牢地掌握着Stackelberg博弈的领导权。

（三）参数敏感度分析

为更好地整合资源，实现社会福利的最大化，本部分考察各参数变化对双方利润、渠道效率、订货倍数、折扣参数的影响，如表1～表3所示。表1～表3中的为优化前零售商利润、制造商利润、优化后零售商利润、制造商利润、优化前的渠道效率，渠道效率为双方独自决策下的利润之和与集中决策下的利润之比。

1.规模参数α变化对最优策略的影响

由表1可知，当α＝10时，制造商虽然制定较低的批发价，但零售商面临过小的市场规模，减少订购量，保证自身不发生亏损；过小的订购量使得制造商的收入不足以弥补生产准备费和生产成本，自然发生亏损。表1中折扣因子对规模参数的变化并不敏感，但呈现减少趋势。由图3知，随着市场规模的扩大，各自的利润均有所增加，并且随着规模参数α的增大，各自的利润呈现加速增大的趋势。

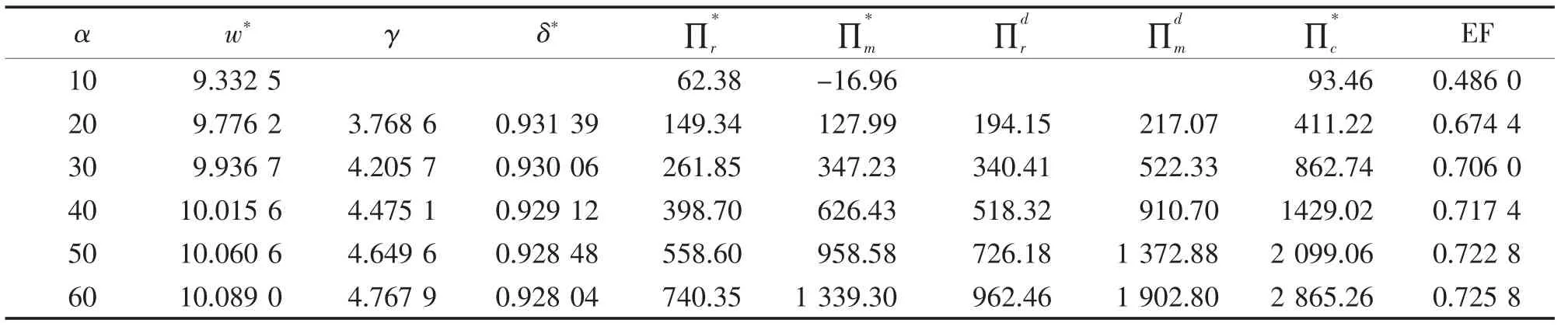
表1 规模参数α的变化对最优策略的影响

2.规模参数β变化对最优策略的影响

由表2可知，随着形状参数β的变化，各参数对形状参数的变化均比较敏感。随着β的增加，最优批发价和订货倍数呈现先增加后降低的趋势。形状参数过小，制造商发生亏损，原因与α值过小相同。协调前的渠道效率随着形状参数的增加呈现增加趋势。折扣因子、各项利润均随形状参数的增加而增加，但批发价呈较少趋势，这是市场规模带来的优势。

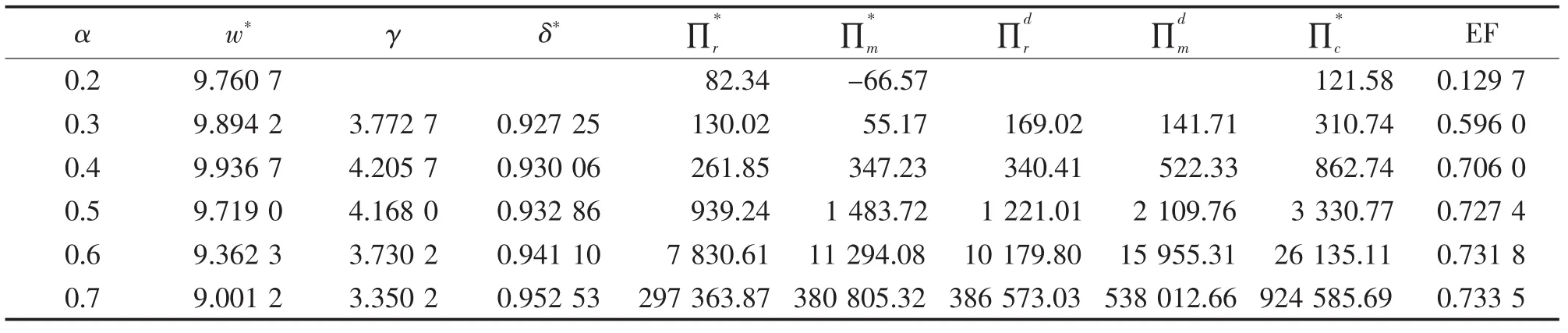
表2 形状参数β对最优策略的影响

3.损耗率θ变化对最优策略的影响

由表3可知，随着θ的增大，批发价与订购量均减少。零售商订购量的减少，使得双方的利润均减少，如图4所示。制造商利润相较于零售商对损耗率θ的变化更加敏感。

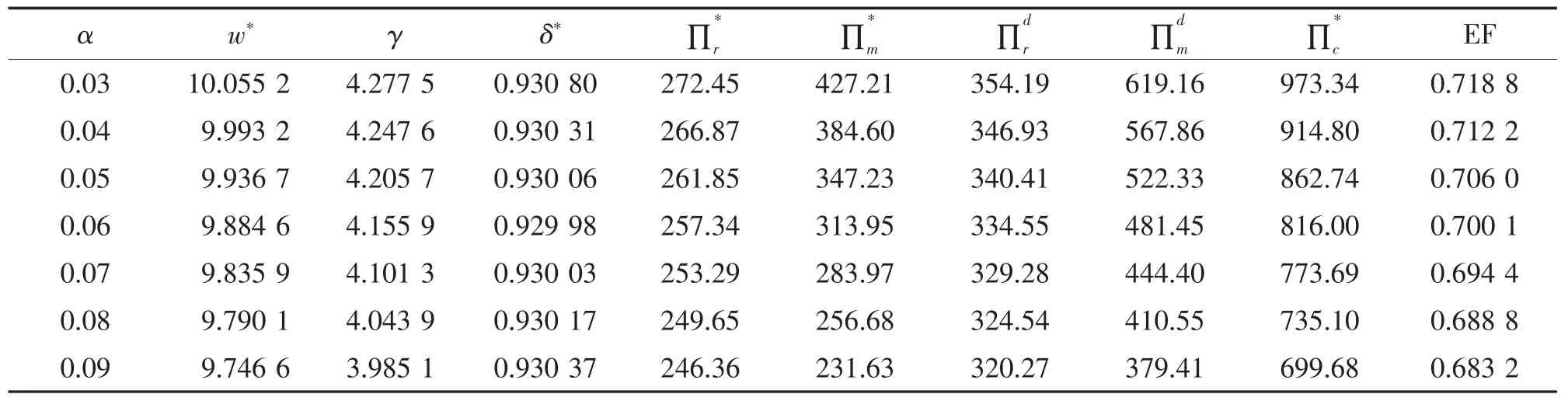
表3 损耗率θ变化对最优策略的影响

4.生产成本及零售价格p对利润的影响

由图5可知，当生产成本过高时，奶制品制造商制定过高的批发价，零售商迫于资金压力减少订购量，从而导致制造商整体销售收入的减少，因成本过高，产生亏损。随着生产成本的增加，制造商给予零售商的批发价随之增加，在高成本的情境下，供应链双方的利润均有所减少，处于供应链领导地位的制造商应设法降低生产成本，因为随着生产成本的减少，各自的利润均有所增加。

由图6可知，零售价格定的过小，零售商减少订货量导致制造商发生亏损，因此过低的零售价格是不现实的。随着零售价p的增加，各方利润均增加，但是过高的零售价是不现实的。

5.存储费ch、订购费Ar与生产准备费Am对利润的影响

由图7可知，在零售价格一定的情况下，随着单位存储成本的增加，零售商减少订货量，导致双方利润的较少。利润减少的趋势越来越平缓。

由图8可知，当零售商订购费足够大时，零售商难以承受这么昂贵的订购费而发生亏损。随着订购费用的增加，零售商利润与制造商利润表现出相反的利润变化趋势。由于零售商需要支付增加的订购费，导致利润减少。

随着订购费的增加，零售商减少订购量，进一步减少了自身的盈利点，但制造商通过提高批发价，减弱了订购量减少带来的利润损失，最后反而使自身利润增加。

由图9可知，分散决策下随着生产准备费用的增加，制造商与零售商呈现出相反的利润变化趋势，奶制品供应商通过降低批发价，刺激零售商订购更多的奶制品，因零售商不用承担生产准备费，随着订购数量的增加，利润自然增加，图9中的零售商利润呈现上升趋势；对于制造商而言，虽然通过降价刺激了零售商订购更多产品，但是依然难以抵消生产准备费的增加额，利润呈现下降趋势。

当生产准备费足够大时，制造商的利润值为负值。对于制造商而言，不参与生产更为明智。集中决策下，由零售商和制造商组成的联盟来承担生产准备费，生产准备费的增加，使得联盟的利润减少，图9中的集中决策下的利润呈现下降趋势。此外，订货倍数、渠道效率随着Am增大而减小。

图3～图9中，协调前的制造商与零售商的利润之和总是小于集中决策时的利润，进一步验证了命题3的正确性。

七、总结与展望

本文探讨了动态需求下的损耗品生产-零售库存优化问题。在假设损耗率为常数的基础上，建立了反映库存水平变化的伯努利方程。在已知期初订货量的情况下，利用泰勒级数展开的方法得到订货周期的解析解。通过灵敏性分析，考察各参数变化对双方及折扣策略的影响。主要结论及管理启示有以下几点。

1.关乎动态需求率的规模参数与形状参数变化均对利益双方产生重要影响，但形状参数相比规模参数对利润的影响更加敏感；零售商可以改变产品的陈列方式，以增加对顾客的吸引；

2.无论是集中决策情形还是分散决策情形，随着损耗率的增大，各自利润均减少；为了增加生产-零售库存系统的利润，应设法降低损耗率；对于蛋糕零售商而言，可以采用新的冷藏设备，在资金不允许采购新的冷藏设备的条件下，可以通过其他方式来降低损耗或变质带来的不利影响，比如降价促销，在蛋糕完全变质之前，清空库存量；

3.随着订购费或生产准备费的增大，制造商与零售商利润呈现相反的变化趋势；零售商与制造商应当设法降低订购费或生产准备费，而不是互相转嫁自身的成本；

4.双方在接受契约的条件下，数量折扣契约可以协调生产—零售库存系统，但协调之后，作为Stackelberg博弈领导者的制造商依然获得协调后的大部分利润，零售商需要进一步强化自身的话语权，从而要求获得更多的利润。

本文的不足之处是假设零售价格不变，实际运作过程中，在保质期临近之前，会采用临时价格折扣，以清空库存，加速资金周转；文章假设损耗率为常数，实际上损耗率受多种因素的影响，现实中的损耗率往往更为复杂；仅研究了一对一的生产—零售库存，但不失一般性。现实当中的需求，既受货架展示量的影响，又受价格影响，后续研究可扩展到需求同时受这两类因素影响的生产-零售库存优化问题；可拓展到损耗率为时变情况下的生产—零售库存问题；亦可拓展到多个制造商和一个零售商组成的生产—零售库存系统，也可进行纵向延伸，考虑多层生产—零售库存系统。

[1]BOLTONJM，LIU WB.CreatinganeffectiveChina“coldsupplychain”—currentstatus，challenges and implementationconsiderations [R/OL].[2011-12-23].http：//www.procuremeleaders.com/8201/23171/SCMChinaColdChinaFINAL110306.pdf.

[2]DYE C Y，OUYANG L Y.An EOQ model for perishable items under stock-dependent selling rate and time-dependent partial backlogging[J].European Journal of Operational Research，2005，163（3）：776-783.

[3]GIRI B C，CHAUDHURI K S.Deterministic models of perishable inventory with stock-dependent demand rate and nonlinear holding cost[J].European Journal of Operational Research，1998，105（3）：467-474.

[4]KROMMYDA I P，SKOURI K，KONSTANTARAS I.Optimal ordering quantities for substitutable products with stock-dependent demand[J].Applied Mathematical Modelling，2015，39：147-164.

[5]YANG C T.An inventory model with both stock-dependent demand rate and stock-dependent holding cost rate[J].International Journal of Production Economics，2014，155（5）：214-221.

[6]DYE C Y，HSIEH T P.Deterministic ordering policy with price-and stock-dependent demand under fluctuating cost and limited capacity[J].Expert Systems with Applications，2011，38（12）：14976-14983.

[7]CHEN Z.Joint decision of inventory and pricing for deteriorating items with partial backlogging and multi-constraint[J]. International Journal of Modelling in Operations Management，2013，3（3）：184-205.

[8]OUYANG L Y，WU K S，YANG C T.A study on an inventory model for non-instantaneous deteriorating items with permissible delay in payments[J].Computers&Industrial Engineering，2006，51（4）：637-651.

[9]CHANG C T，CHENG M C，OUYANG L Y.Optimal pricing and ordering policies for non-instantaneously deteriorating items under order-size-dependent delay in payments[J].Applied Mathematical Modelling，2015，39：747-763.

[10]ARCELUS F J，SHAH N H，SRINIVASAN G.Retailer’s pricing，credit and inventory policies for deteriorating items in response to temporary price/credit incentives[J].International Journal of Production Economics，2003，81：153-162.

[11]MAIHAMI R，KARIMI B.Optimizing the pricing and replenishment policy for non-instantaneous deteriorating items with stochastic demand and promotional efforts[J].Computers&Operations Research，2014，51（3）：302-312.

[12]HWANG H S.A study on an inventory model for items with weibull ameliorating[J].Computers&Industrial Engineering，1997，33（3）：701-704.

[13]CHENG M，ZHANG B，WANG G.Optimal policy for deteriorating items with trapezoidal type demand and partial backlogging [J].Applied Mathematical Modelling，2011，35（7）：3552-3560.

[14]DAS B C，DAS B，MONDAL S K.An integrated inventory model with delay in payment for deteriorating item under Weibull distribution and advertisement cum price-dependent demand[J].International Journal of Operational Research，2014，20（3）：341-368.

[15]徐贤浩，余双琪.短生命周期产品的三种库存模型的比较[J].管理科学学报，2007，10（4）：9-15.

[16]CHANG C T，TENG J T，GOYAL S K.Optimal replenishment policies for non-instantaneous deteriorating items with stockdependent demand[J].International Journal of Production Economics，2010，123（1）：62-68.

[17]TENG J T，OUYANG L Y.An EOQ model for deteriorating items with power-form stock-dependent demand[J].International Journal of Information&Management Sciences，2005（1）：1-16.

[18]WU K S，OUYANG L Y，YANG C T.An optimal replenishment policy for non-instantaneous deteriorating items with stockdependent demand and partial backlogging[J].International Journal of Production Economics，2006，101（2）：369-384.

[19]HOU K L.An inventory model for deteriorating items with stock-dependent consumption rate and shortages under inflation and time discounting[J].European Journal of Operational Research，2006，168（2）：463-474.

[20]段永瑞，李贵萍，霍佳震.部分延迟订购的Weibull分布变质品库存策略研究[J].管理工程学报，2013（3）：205-213.

[21]黄卫来，黄松华.Weibull分布变质物品库存模型研究[J].工业工程与管理，2007，12（2）：72-75.

[22]SAHA S，GOYAL S K.Supply chain coordination contracts with inventory level and retail price dependent demand[J]. International Journal of Production Economics，2015，161：140-152.

[23]SARATHI G P，SARMAH S P，JENAMANI M.An integrated revenue sharing and quantity discounts contract for coordinating a supply chain dealing with short life-cycle products[J].Applied Mathematical Modelling，2014，38（15）：4120-4136.

[24]MIRZAEE M，MAKUI A，TAVAKOLI E.Supply chain coordination under retail competition and advertising dependent demand [J].International Journal of Industrial Engineering Computations，2012，3（3）：383-392.

[25]陈军，但斌.基于实体损耗控制的生鲜农产品供应链协调[J].系统工程理论与实践，2009（3）：54-62.

[26]ZHOU Y W，MIN J，GOYAL S K.Supply-chain coordination under an inventory-level-dependent demand rate[J].International Journal of Production Economics，2008，113（2）：518-527.

Optimization of Dynamic Demand and Deterioration Products Production-inventory Model

FU Kaifang，CHEN Zhixiang
（School of Business，Sun Yat-Sen University，Guangzhou 510275，China）

In this article，we study the problem of optimization of Production-inventory model of one manufacturer and one retailer，in which the manufacturer produces deterioration products and the retailer’s demand is stock-dependent demand.Aiming at the problem of low efficiency of decentralized decision making，a quantity discount contract is established to make the manufacturer and retailer obtain the advantage of centralized decision in their independent decision-making.Products sales data from a cake shop was used to carry out?the application of the model;?the results showed that when the production cost was too high，the manufacturer took a loss;when the retail price was too low，the retailer reduced order quantities，thus making the manufacturer take a loss.The higher storing cost，the lower profit of the manufacturer and the retailer.When ordering cost or production cost increase，the profit of the manufacturer and the retailer shows opposite trend.Both sides of the manufacturer and the retailer were sensitive to the change of the scale parameter and shape parameter，but were more sensitive to the change of the shape parameter.With the increase of the rate of loss，the profit of the manufacturer and the retailer decreased.The quantity discount contract could coordinate the productioninventory system，because of different discourse power，the manufacturer still got most profit after coordination.

dynamic demand；deterioration products；decentralized decision；centralized decision；quantity discount

F406；O22

A

1009-3370（2016）06-0070-10

10.15918/j.jbitss1009-3370.2016.0609

[责任编辑：宋宏]

2016-02-22

国家自然科学基金资助项目（71372154）

伏开放（1988—），男，博士研究生，E-mail：kaifangfu@sina.com；陈志祥（1965—），男，教授，博士生导师，E-mail：mnsczx@mail. sysu.edu.cn