电子罗盘的标定方法研究

中国船舶重工集团公司第七一〇研究所，湖北 宜昌 443003

一、引言

电子罗盘是一种重要的导航工具，它含有一个三轴加速度计和一个三轴磁强计，是一种常用的导航设备。随着MEMS技术的发展，电子罗盘在导航领域的应用越来越广泛。

目前，在各种导航技术中，基于MEMS加速度计和磁强计的低成本电子罗盘由于其体积小、重量轻、成本低、不受外界干扰、输出频率高等优点，应用范围越来越广。然而，MEMS惯性器件有一个致命的缺点—长期稳定性较差，存在明显时漂现象，再加上加工、制造工艺不完善等均可造成敏感元件的输出误差，通常元器件的误差占到整个系统误差的90%以上[1]，因此在使用前必须对各个传感器的误差系数进行标定。

对电子罗盘的标定要分别对加速度计和磁强计的误差来源进行分析，并建立相应的数学模型。MEMS惯性元器件的误差模型可以分为静态误差模型、动态误差模型和随机误差模型[2]。动态误差与元器件的角运动相关，到目前为止，针对动态误差模型的研究尚不十分充分。随机误差包括偏置漂移、随机噪声等，只有通过建立随机模型，将其加入到Kalman滤波器状态矢量中进行估计并补偿。

本文主要针对MEMS加速度计和磁强计建立了静态误差标定模型，给出利用位置转台即可实现的简易标定方法，使用简捷的数学运算实现误差系数的标定。

二、静态误差类型

一般来说，对MEMS惯性器件进行静态误差建模需要考虑惯性器件的零偏和刻度因子等系数。在惯性系统中，惯性器件已经安装在系统中，并且需要将三个轴向的惯性器件进行整体标定，这时候需要将安装误差考虑进来。因此，对于惯性器件的标定模型，需要综合考虑零偏、刻度因子和安装误差等因素[3]。

零偏误差是指输入为零时惯性器件的输出值，一般认为它是常值，但是实际上由于受外部条件的影响，它是在一定范围内随机变化的。对于磁强计来说，其零偏就是由硬磁干扰所引起的偏差。本文中，设定加速度计和磁强计的零偏均为常值。

惯性器件的输出与单位量之间的比值称为惯性器件的刻度因子[4]，它是通过标定试验测定的，其数值预先存储在计算机里，在导航解算时，计算机每次采样后都要将采样值除以刻度因子，以便得到实际值。但是标定试验时，惯性器件所处的工作环境、温度、振动和电磁干扰等与实际的工作环境有很大的差异，这将导致惯性器件工作过程中实际的刻度因子与存储在计算机里的刻度因子不一致，这就是刻度因子误差。

电子罗盘直接固联在载体上，这样惯性器件的输入轴应和载体坐标系的坐标轴线完全一致，但实际上安装时总是存在着一定的安装误差，使得惯性器件的X轴不仅敏感X轴的输入，还会敏感Y轴和Z轴的输入，因此惯性器件敏感轴构成的坐标系就和载体系之间存在一个失调矩阵。

另外由于磁强计的特殊性，在其内部还存在有软磁干扰[5]，这同样会引起磁强计的测量误差，在标定时必须予以考虑。

三、加速度计的标定

首先根据上述误差类型分析，建立加速度计的标定模型。

设加速度计原始测量数据为Ax、Ay、Az，经过标定后数据为Ax1、Ay1、Az1，则它们之间的关系可以表示为下式：

式中，[A_m]3×3—加速度计敏感轴和载体系之间的失调矩阵，它的对角线元素全为1[6]；

A_SCi(i=x, y, z) —加速度计三个轴的刻度因子；

A_OSi(i=x, y, z) —加速度计三个轴的零偏。

将式（1）中间三项中的最后一项展开，然后分别做矩阵乘积运算即可得到ACC10到ACC33共12个参数。

由式（1）可知，加速度计的标定即为确定从ACC10到ACC33的12个参数。

将式（1）进一步可写为：

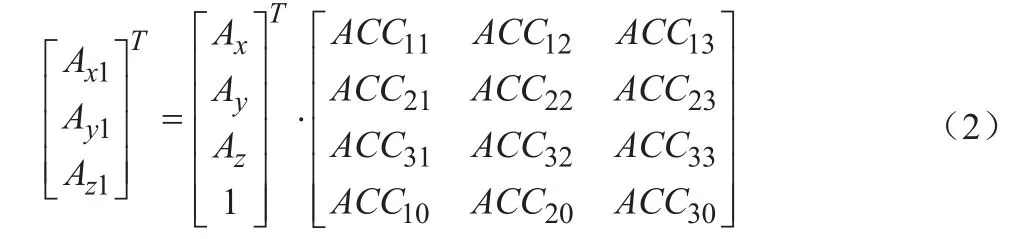
更进一步可表示为：

式中，X—表示12个标定参数矩阵；

W—表示加速度计原始测量数据向量；

Y—表示标定后数据向量。

下面将电子罗盘置于位置转台上，分别采样加速度计X、Y、Z轴垂直向上、向下6个位置的静止数据。

Z轴垂直向下时（P1位置），采样n1组原始数据，则：

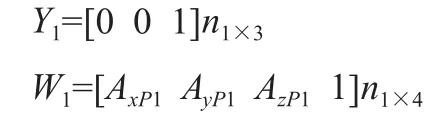
Z轴垂直向上时（P2位置），采样n2组原始数据，则：

Y轴垂直向下时（P3位置），采样n3组原始数据，则：

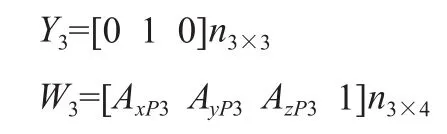
Y轴垂直向上时（P4位置），采样n4组原始数据，则：

X轴垂直向下时（P5位置），采样n5组原始数据，则：

X轴垂直向上时（P6位置），采样n6组原始数据，则：

下面记：n=n1+n2+n3+n4+n5+n6，则式（3）可以表示为：

式中：

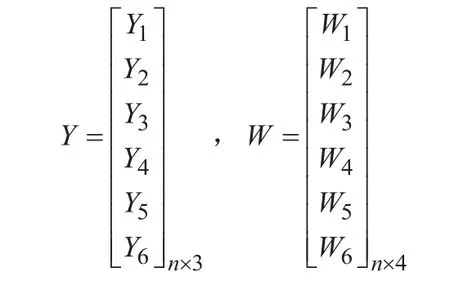
利用最小二乘法解方程（4）可得：

由此，便可确定式（1）中的12个标定参数。为使结果更加准确，可以重复进行多次计算，最后取均值。

为使标定更加精确，也可以选取Ax=0,Ay=±0.707g,Az=-0.707g或者Ax=±0.707g,Ay=0,Az=-0.707g等位置进行计算，或者用这些点来验证实验结果的准确性。

四、磁强计的标定

设加速度计原始测量数据为Mx、My、Mz，经过标定后数据为Mx1、My1、Mz1。则它们之间的关系可以表示为下式：

式中，[M_m]3×3—磁强计敏感轴和载体系之间的失调矩阵；

M_SCi(i=x, y, z) —磁强计三个轴的刻度因子；

M_OSi(i=x, y, z) —硬磁干扰引起的偏差；

[M_si]3×3—软磁干扰引起的偏差矩阵。

当载体做3D旋转时，由于上述误差因素的存在，我们根据磁强计的测量值作图可以得到一个失真的椭球，其数学模型可以表示如下：

式中，x、y、z—磁强计原始测量值

Mx、My、Mz，x0、y0、z0—硬磁干扰引起的偏差M_OSi(i=x, y, z)；

a、b、c—椭球半轴长；

d、e、f—使椭球产生倾斜的横轴效应；

R—当地地磁场强度（常值）。

假设不存在软磁干扰，或者说软磁干扰非常小可以忽略，则[M_si]3×3可以认为是单位阵，这样式（7）可以简化为：

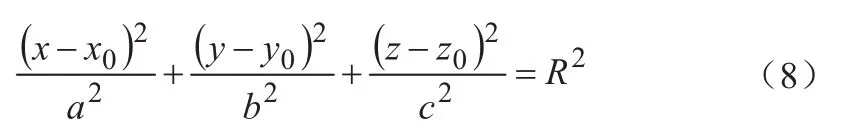
由式（8）又可求得：

式中的W、H、X和式（9）中的矩阵依次对应。

当载体在3个平面内旋转时，记录n个x、y、z，联立后可得：

利用最小二乘法解方程可得：

设：X=[x1x2x3x4x5x6]T

当存在软磁干扰时，相似地，利用上述方法仍然可以确定[M_si]3×3，由于计算比较复杂，这里不再详述。

至此，除了失调矩阵[M_m]3×3之外其他的误差因子均已确定，下面分析[M_m]3×3的确定方法。

则式（16）可简记为：

经过了刻度因子、硬磁干扰和软磁干扰的标定之后，载体旋转时磁强计测量值所形成的椭球的中心应在坐标系原点，但是轴向仍然有偏差存在，当Z轴垂直向下时，采样m次，得到参数如下：

故Z轴向下时的归一化单位向量为：

式中：X3×1=[X1X2X3]

同理，当X轴、Y轴垂直向下时可以得到Rx、Ry，故：

至此，所有误差因子均已确定。

五、验证实验

对于加速度计的标定，可以使用三轴位置转台来实现。如图1所示为实验所用位置转台。

具体标定步骤如下：

（1）将电子罗盘通过夹具固定在三轴转台上，保证电子罗盘轴向与转台轴向平行，通电预热30min；

（2）设置好电子罗盘输出数据采样频率，将电子罗盘分别按照加速度计的X、Y、Z轴垂直向上、向下共6个位置固定安装，并分别采样加速度计输出数据，并保存，每个位置的采样时间为2min；

（3）按照第三章中的方法进行计算，即可完成加速度计的标定。

对于磁强计的标定，则需要使用工装六面体，具体步骤如下：

（1）将电子罗盘通过夹具固定在工装六面体内，保证电子罗盘正交的三个面与六面体的相应面平行，通电预热30min；

（2）设置好电子罗盘输出数据采样频率，将电子罗盘分别按照磁强计的X、Y、Z轴垂直向上、向下共6个位置固定安装，并分别采样磁强计输出数据，并保存。每个位置的采样时间为2min;

（3）按照前文方法进行计算，即可完成磁强计的标定。

六、结论

此标定方法仅需使用普通的位置转台和工装六面体即可实现。实验表明，可以有效地提高导航系统的精度，使姿态角的精度达到2°以内，可以满足大部分手持设备的导航精度要求。

此标定试验未考虑环境温度及周围测量噪声的影响，也没有考虑加速度二次项误差，因此还有待进一步完善。