三相四桥臂逆变器的三角波辅助控制策略

马海啸， 叶海云， 龚春英

(1.南京邮电大学 自动化学院，江苏 南京 210023；2.南京航空航天大学 自动化学院，江苏 南京 210016)



三相四桥臂逆变器的三角波辅助控制策略

马海啸1， 叶海云1， 龚春英2

(1.南京邮电大学 自动化学院，江苏 南京 210023；2.南京航空航天大学 自动化学院，江苏 南京 210016)

针对三相四桥臂逆变器常用的控制方法或者属于开环控制,或者需要大量繁琐的计算,不适用于对动静态性能要求较高的中高频逆变场合这一缺点,提出一种三相四桥臂逆变器的三角波辅助控制策略。该控制策略依据电压电流双闭环控制原理,通过对三相四桥臂逆变电路建立电压电流方程,推导三相输出电压对称所需要的条件,从而发现三角波在各相桥臂的控制中起到至关重要的作用。前三相桥臂在电压电流双闭环控制的基础上在调制信号中注入三角波,使得调制比可以大于1,提高了逆变器的直流电压利用率;第四桥臂则利用构造出的三角波作为调制信号进行PWM控制,确保逆变器在不平衡负载条件下输出电压对称。设计一台6 kVA 原理样机,仿真和实验结果证明了该控制策略的可行性。

三相四桥臂逆变器; 三角波; 双闭环控制; 对称分量法; 零序谐波

0 引 言

随着电力电子的快速发展,各种不平衡负载的应用越来越普遍,常要求三相逆变器具有带不平衡和非线性负载的能力[1]。

三相四桥臂逆变器[2]在三相桥式逆变器的基础上增加了一个桥臂形成中性点,使三相四桥臂可以产生三个独立的电压,从而使其有在不平衡负载下维持三相电压对称的能力,从而受到了各国学者的广泛青睐。

目前常见的三相四桥臂逆变器的控制策略主要有以下几种:空间矢量控制法[3-6],该方法通过用一稳态参考矢量的匀速定幅旋转,来保障三相电压的输出要求,并根据负载和输入电压的变化相应地改变参考矢量幅值的大小,从而达到调压的目的,但在负载变化或负载情况不明时,很难实现实时控制。通过实时检测三相负载电流和直流母线电压可计算确定三相基准电压给定,使之适用于任意时变线性负载的场合,但该方法增大了数据的计算量,逆变器动态性能不高。在空间矢量控制的基础上也有学者提出将正序、负序和零序分量分别来控制从而获得四个桥臂控制的解耦[13-16],但这种方法同样无法避开坐标变换的数学计算,在中频逆变器中由于开关频率相对较高,较大的计算量不利用逆变器动静态性能的提高。开关点预置控制[7-8]通过对前三桥臂的开关角预置,消除不含零序谐波的低次奇次谐波,对第四桥臂的开关角预置消除低次零序谐波。控制原理简单易于实现,但属于开环控制方式,逆变器动态性能也不会太高。滞环电流控制[9-10]要求反馈电流在给定的环宽范围内变化,从而实现反馈电流跟踪给定电流的目的。但用在四桥臂逆变器的控制时,需要对各相误差电流大小进行判断来决定第四桥臂开关管的开关状态,由于检测判断存在误差,因此控制精度也较难让人满意。文献[11-12]提出一种解耦控制方案,把三相滤波电感和零线滤波电感看作电源内阻抗,通过引入变量及变换控制的方式,经等效变换将零线阻抗变换为零,从而将复杂的三相电压控制转化为单相电压进行控制,便于SPWM控制,但该控制方法的控制参数的选择与逆变器电感参数相关,控制器设计较为繁琐,且不利于电感参数的优化。

为了简化逆变器控制中的运算和判断,提高中频三相四桥臂逆变器的电气性能,本文提出了一种包含三角波辅助控制的双闭环控制策略。

1 四桥臂逆变器输出电压对称的条件

三相四桥臂逆变器的主电路拓扑结构如图1所示。

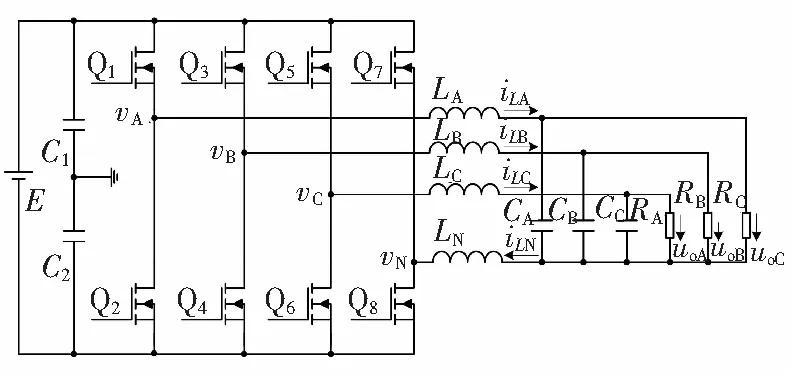
图1 三相四桥臂逆变器主电路拓扑

开关管Q1～Q6构成逆变器的A、B、C三相桥臂,Q7～Q8构成逆变器四桥臂。LA、LB、LC分别为A、B、C三相滤波电感,LN为第四桥臂滤波电感,CA、CB、CC分别为A、B、C三相滤波电容,RA、RB、RC分别为逆变器A、B、C三相负载。

为方便分析,假设直流电源电压E由电容C1、C2一分为二,两电容中点为参考电位,三相桥臂中点和第四桥臂中点相对于参考电位的电压分别为vA、vB、vC和vN,三相电感电流和第四桥臂电感电流分别为iLA、iLB、iLC和iLN,三相输出电压为uoA、uoB、uoC,三相滤波电感值对称LA=LB=LC=L,三相滤波电容值对称CA=CB=CC=C。根据基尔霍夫电压和电流定律可得

(1)

iLN=iLA+iLB+iLC。

(2)

将式(1)中的三个等式左右两边分别相加,并且再将式(2)代入可得

(3)

性能优良的三相逆变器在带三相不平衡负载时其三相输出电压也能维持较好的对称性。那么不妨假设逆变器的三相输出电压完全对称,在任意的不平衡负载条件下满足式(4):

uoA+uoB+uoC=0。

(4)

另外为了方便三相四桥臂逆变器控制策略的实现,通常各相桥臂的控制采用对称控制,因此各相桥臂中点的电势vA、vB和vC也是对称的。那么,如果忽略vA、vB和vC中的高频开关分量也可以得到

vA+vB+vC=0。

(5)

将式(4)和式(5)代入式(3)整理可得

(6)

从式(6)可以看出,对vN控制的核心思想是保证第四桥臂流过电流的数值等于iLA+iLB+iLC。于是可以得出结论:若三相四桥臂逆变器各相的给定基准电压为对称正弦波,那么对第四桥臂的控制只要能使第四桥臂流过的电流是三相电感电流之和,就能保证在不平衡负载条件下,逆变器三相输出电压对称。

由于第四桥臂只流过零序电流,因此对第四桥臂的控制实际也可理解成对零序电压控制。于是得到一个推论:如果能利用前三桥臂的电感电流信息构造一个零序调制信号对第四桥臂进行控制,也可以保证不平衡负载条件下,逆变器三相输出电压对称。

从结论和推论可以看出,对于第四桥臂的控制必须依赖三相电感电流的信息。如果前三桥臂采用开环控制或单电压闭环控制,由于三相电感电流的信息是无法得到的,所以很难实现三相四桥臂逆变器的优化控制,而拥有电流环的控制方法,理论上具备了实现其优化控制的可能性。

2 四桥臂逆变器三角波辅助控制策略

三相四桥臂逆变器的三角波辅助控制策略的具体方案包括两个部分:前三桥臂(A、B、C三相)的电压电流双闭环PWM控制和第四桥臂(中线)的三角波构造开环控制。

2.1 前三桥臂电压电流双闭环PWM控制

为了满足式(5)的关系,前三桥臂可以利用传统的三相电压电流双闭环PWM控制,控制框图如图2所示。

A相反馈的输出电压uoAf与A相电压基准信号uA比较后经过电压控制器(PI调节器)产生电压外环的输出。电压外环的输出作为电流内环的给定iA*,A相反馈的电感电流iLAf与iA*比较后经过电流控制器(P调节器)产生电流内环的输出uka,uka作为A相的调制波跟三角载波交截产生开关管Q1、Q2的控制信号。图中Kuf和Kif分别为电压采样系数和电流采样系数。由于A、B、C三相控制方案类似,因此B、C相的原理类似,在此不再重复叙述。

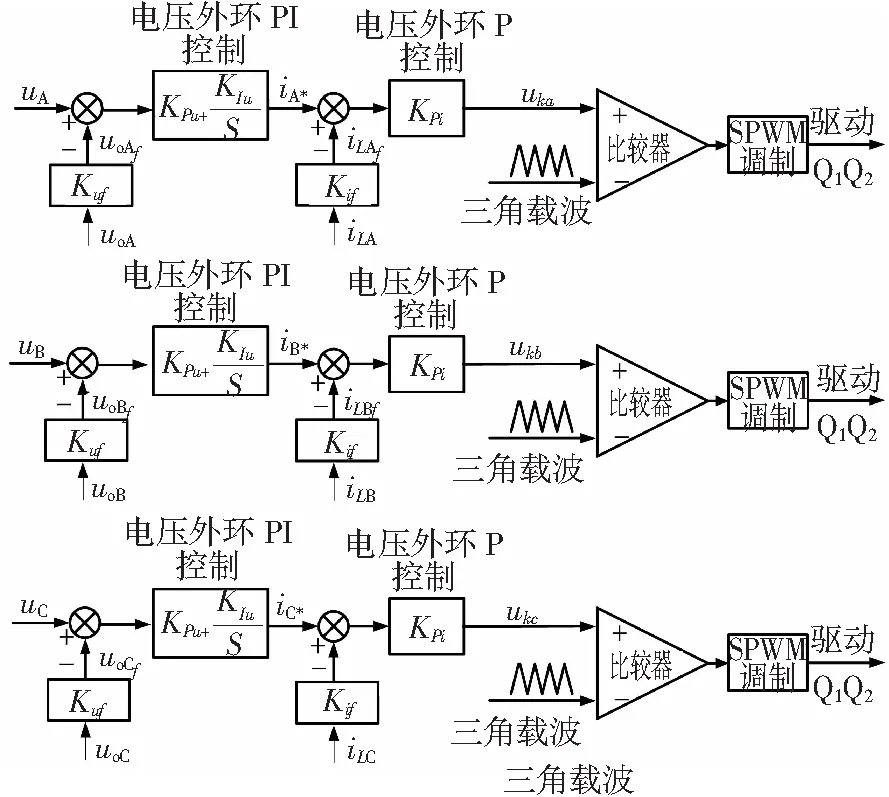
图2 前三桥臂控制框图

之所以采用该双闭环控制方案的原因是:(1) 电压给定为对称三相正序电压,符合三相输出电压的期望;(2) 即使逆变器三相负载为不平衡负载,逆变器负载电流不平衡,但通过电流环的调节可以保证电流环的输出,也就是前三桥臂的最终的调制信号uka、ukb和ukc为对称三相电压而满足式(5)。

2.2 第四桥臂三角波构造开环控制

第四桥臂三角波开环控制是通过构造一个三角波作为调制波,再将该三角调制波跟高频三角载波交截,产生第四桥臂两个开关管的控制信号。

首先来分析一下第四桥臂选用三角波作为调制波进行控制的原因。

假设正弦波的瞬时值为usin,其幅值为Usin,角频率为ω,初相角为0度;三角波的瞬时值为utr,其幅值为Utr,角频率为ωtr,初相角为0度。那么分别可得到正弦调制波的数学表达式和三角波的傅里叶级数展开表达式为

usin=Usinsinωt，

(7)

(8)

其中k为整数。

如果令ωtr=3ω。于是式(8)变为

(9)

从式(9)可以看到,当三角波的频率是正弦波频率的3倍时,三角波可以看成是正弦波的3、9、15次等谐波的叠加。很显然3、9、15次等谐波都是零序谐波,因此利用三角波作为第四桥臂的调制波,实际就是一种对零序电压控制的方案,满足前面分析的推论,因此可保证不平衡负载条件下,逆变器三相输出电压对称。

其次来分析一下三角调制波的构建方法。

第四桥臂控制信号的构建必须包含前三桥臂电感电流的信息,因此可以利用前三桥臂电流环的输出来构造第四桥臂控制信号。

当负载不平衡时,各相电感电流是不平衡的,但经过电流闭环后生成的各相调制信号uka、ukb、ukc为对称三相正弦波。假设其波形如图3所示。

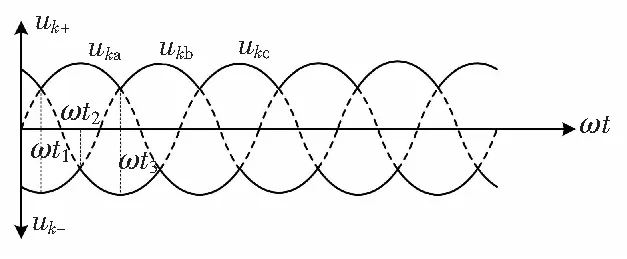
图3 三相调制波形

观察图3波形中的虚线部分可以发现,其波形形状非常接近三角波且频率为正弦波的3倍。于是该虚线波形就是需要构造的波形。

假设uka、ukb、ukc表达式为

(10)

可以得到uka、ukb、ukc的正向包络线波形uk+和负向包络线波形uk-,如图3中的实线波形。根据式(10),可得uk+和uk-的数学表达式分别为

(11)

(12)

将式(11)和式(12)进行傅里叶级数展开,并求其和,再反相,可得到表达式:

(13)

对比式(13)和式(9)可以发现,ukN的确为频率是调制波3倍的三角波,且三角波的幅值为

(14)

于是可以得到第四桥臂控制方法是将uka、ukb、ukc输入给三角波生成电路,该三角波生成电路利用三相正负包络线叠加的原理构造第四桥臂的三角波调制信号ukN,然后再将ukN跟三角载波进行交截产生Q7、Q8的控制信号,控制框图如图4所示。

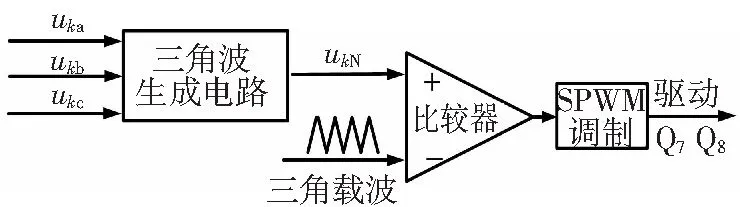
图4 第四桥臂控制框图

3 改进的三角波辅助控制策略

从上面分析可以看到第四桥臂利用构造的三角波辅助控制是本控制策略的核心思想,但该方法调制比不能大于1,也就是说相电压直流电压利用率不超过0.5,直流电压利用率较空间矢量控制的三相四桥臂逆变器低。

为了提高直流电压利用率,研究了一种改进的三角波辅助控制策略,通过在三相正弦调制波中注入三角波来压低合成波形的峰值,使调制比可以大于1,从而达到提高直流电压利用率的目的。

3.1 改进的三角波辅助控制原理

很显然注入的三角波不能使用开环的方法生成,原因是本文中的三相正弦调制波是经过闭环控制得到的,因此没法知道调制波的准确相位。

但观察用来控制第四桥臂的三角波,如图3中虚线表示的波形,可以发现如果把该波形叠加到uka、ukb、ukc中去,刚好可以压低uka、ukb、ukc的峰值。从而可以使调制比大于1,提高逆变器的直流电压利用率。于是得到三相四桥臂逆变器改进的三角波辅助控制原理框图如图5所示。

控制方案同样包括前三桥臂(A、B、C三相)的控制和第四桥臂(中线)的控制两个部分。前三桥臂的控制和第二小结提到的方法相比增加了三角波ukN的注入。第四桥臂的控制跟第二小结提到的方法相同。

当uka、ukb、ukc中注入ukN以后,式(5)不再成立,变为:

vA+vB+vC=3vtr。

(15)

式中vtr为注入的三角波产生的调制波形。

将式(4)和式(15)代入式(3)整理可得

(16)

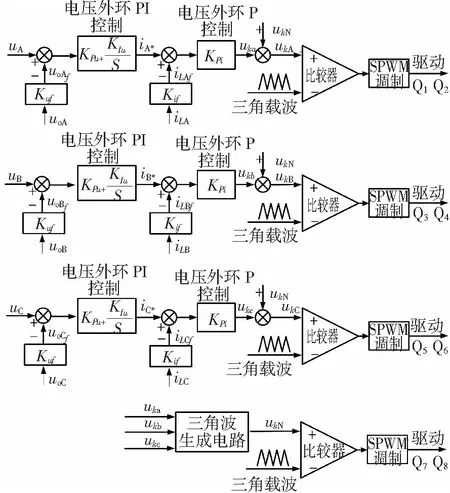
图5 改进的三角波辅助控制策略

Fig. 5 Improved control method using an

auxiliary triangle wave

由于第四桥臂只流过零序电流,注入的三角波也是零序谐波,于是可以得到只要vN用零序谐波电压进行控制,就可以保证不平衡负载条件下,逆变器三相输出电压对称。而第四桥臂使用三角波辅助控制显然满足这一结论。

3.2 三角波注入幅值与最大直流电压利用率

从图3可以看到,注入的三角波其初相角为零度,那么A相正弦调制波叠加三角波以后的表达式为

ukA=Usinsinωt+

(17)

由于当ωt=π/6时,三角波取得正向峰值,之后正弦波幅值增加,三角波幅值减小,这种情况下只要能保证三角波下降的速度比正弦波增加的速度快,那么ωt=π/6就是ukA的极大值点,且极大值为

(18)

式(18)满足的条件是

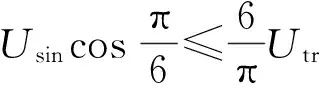
(19)

根据式(18)和式(19),如果以Utr为变量,可以得到,当Utr=0.45Usin时,UkAmax为0.95Usin。可见三角波和正弦波叠加后的合成波形的幅值较正弦波的幅值小,这有利于提高直流电压利用率。

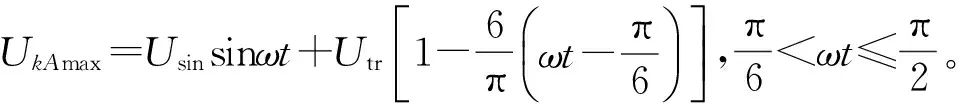
(20)

从式(20)可以看到,式中有两个可变量一个是Utr,另一个是ωt,如果确定了Utr的值,就可算出极值点所对应的ωt的值,从而计算出UkAmax的值。表1列出了一组计算结果。

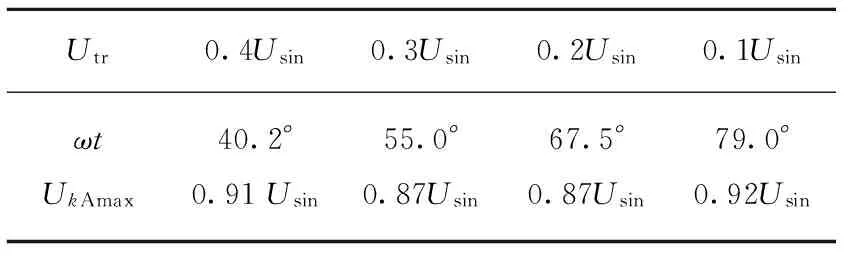
表1 UkAmax计算结果

从计算结果可以看到,当注入的三角波的幅值是正弦波幅值的0.2～0.3倍时,UkAmax的数值较小,这种情况下直流电压利用率大约可以提高15%。

综合以上分析,改进的三角波辅助控制策略在三相调制波中注入控制第四桥臂的三角波,不但不会影响三相四桥臂逆变器的带不平衡负载能力,还可有效压低调制波的幅值,提高了逆变器的直流电压利用率。

4 仿真结果

利用Saber仿真软件对三相四桥臂逆变器的三角波辅助控制策略进行了仿真,仿真电路参数为:输入电压300 VDC,开关频率20 kHz,输出三相电压115 VAC,频率400 Hz,三相额定功率6 kVA,三相滤波电感180 μH,滤波电容25 μF,中线电感 17 μH。

图6给出了无三角波注入和改进后有三角波注入的不平衡负载下的逆变器仿真对比波形。图中uoA、uoB、uoC分别表示A、B和C相的输出电压,iLA、iLB和iLC分别表示A、B和C相电感电流。

从图中各相电感电流波形可以看到三相负载是不平衡的,但三相输出电压依然保持平衡,这说明本控制策略可确保三相四桥臂逆变器具有较强的带不平衡负载的能力。但是对于改进后有三角波注入的控制方法,由于直流电压利用率高,在相同直流输入电压情况下,逆变器输出电压正弦度明显好于无三角波注入的控制方法,电感电流的脉动也有所减小。

图6 不平衡负载仿真波形

图7为采用改进后控制方法的A、B、C三相和第四桥臂的调制信号仿真波形。

图7 调制信号仿真波形

从波形可以看到第四桥臂的调制信号ukN并不是一个理想的三角波,而是一个存在一定脉动的三角波,这是因为三相电流环输出的波形必然存在脉动,那么由三相电流环输出波形合成的ukN必然也存在一定脉动。此外还可以看到注入了ukN的三相调制波ukA、ukB、ukC已经变成了鞍形波,这样可使逆变器调制比大于1,从而有效提高逆变器的直流电压利用率。

5 实验验证

设计了一台跟仿真参数一致的实验原理样机,采用改进后的三角波辅助控制策略,可以得到以下实验波形。

图8为原理样机三相空载时的三相输出电压的实验波形。

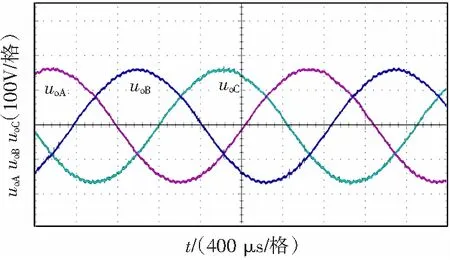
图8 空载实验波形

图9为原理样机三相带额定阻性负载时的三相输出电压、三相电感电流和中线电感电流实验波形。

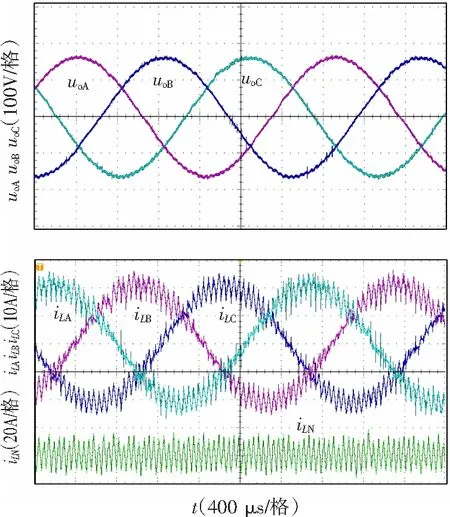
图9 额定负载实验波形

图10为原理样机三相带不平衡阻性负载时的三相输出电压、三相电感电流和中线电感电流实验波形。

由以上实验结果可以看出,采用改进的三角波辅助控制的三相四桥臂逆变器无论在平衡负载还是不平衡负载情况下三相输出电压正弦度较高,THD不大于1.5%,三相输出电压也较对称,电压幅值不平衡不大于±1%。

在相同参数下,采用未改进的无三角波注入的控制方法也进行了类似的实验,实验结果表明输出电压如果要达到以上波形的质量,逆变器直流输入电压需要加至340 V,高于改进控制方法的300 V,否则就会出现类似图6(a)中的输出电压畸变。可见改进的控制方法有利于提高逆变器直流电压利用率。

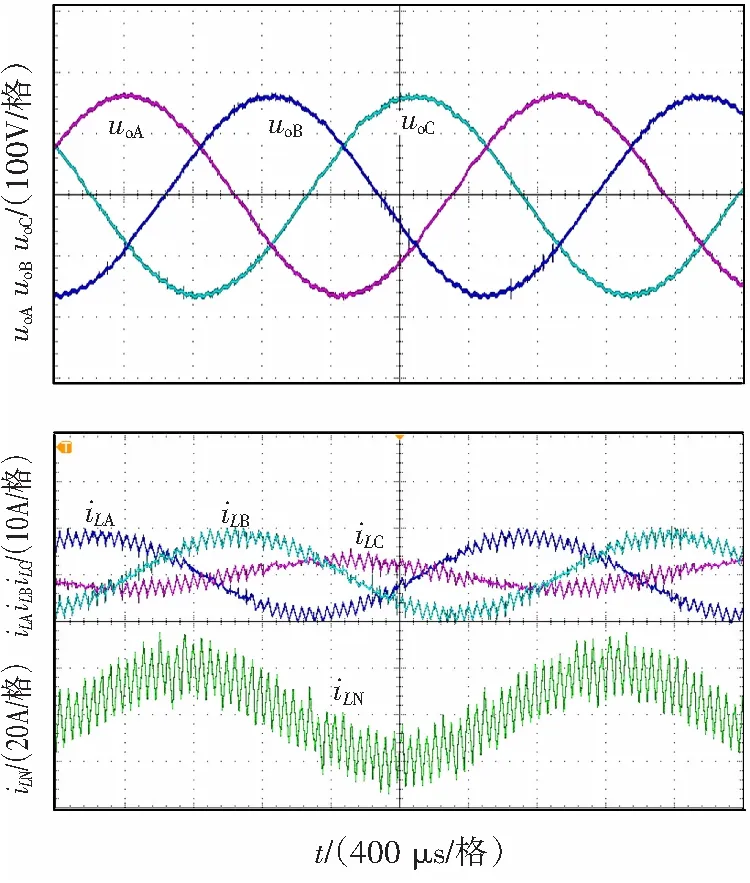
图10 不平衡负载实验波形

6 结 论

本文提出了一种三相四桥臂逆变器的三角波辅助控制策略及其改进方法,给出了所需三角波的构造方法,分析了三角波幅值对直流电压利用率的影响,从整个控制策略看具有原理简单易实现的特点。针对该控制策略进行了仿真和实验验证,结果表明该控制策略还具有以下特点:①无论是三相平衡负载或是三相不平衡负载,逆变器输出电压波形正弦度较高,THD可达1.5%以下,输出电压对称形较好,电压幅值不平衡不超过±1%;②前三桥臂可采用三角波注入控制也可以不采用三角波注入控制,这对逆变器输出电压的正弦度和对称性影响不大,但采用三角波注入的方案比不采用的方案直流电压利用率约高15%。

[1] 刘德红,汪光森,胡安,等. 三相逆变器在不平衡负载下的2种调制策略对比[J]. 电力自动化设备,2009,29(1):41-45.

LIU Dehong,WANG Guangsen,HU An et al. Comparison between two modulation strategies of three-phase inverter with unbalanced load[J]. Electric Power Automation Equipment,2009,29(1):41-45.

[2] 董锋斌,皇金锋,傅周兴. 一种三相四桥臂逆变器的数学模型分析[J]. 电力自动化设备,2011,31(6): 98-101.

DONG Fengbin,HUANG Jinfeng,FU Zhouxing. Analysis of mathematical model for three-phase four-leg inverter[J]. Electric Power Automation Equipment,2011,31(6):98-101.

[3] OLORUNFEMI Ojo, PARAG M Kshirsagar. Concise Modulation Strategies for Four-leg Voltage Source Inverter[J]. IEEE Transactions on Power Electronics, 2004, 19(1): 46-53.

[4] DHAVAL C Patel, RAJENDRA R Sawant, MUKUL C Chandorkar. Three-dimensional flux vector modulation of four-leg sine-wave output inverters[J]. IEEE Transactions on IE, 2010, 57(4):1261-1269.

[5] 熊宇. 基于DSP的四桥臂三相逆变器研究[D]. 南京:南京航空航天大学,2003.

[6] 龚春英, 熊宇, 郦鸣, 等. 四桥臂三相逆变器电源的三维空间矢量控制技术研究[J]. 电工技术学报, 2004, 19(12): 29-36.

GONG Chunying, XIONG Yu, LI Ming, et al. Study of space vector modulation of four-legged three-phase inverter[J]. Transactions of China Electrotechnical Society, 2004, 19(12): 29-36.

[7] 王慧贞, 丁勇, 张方华, 等. 开关点预置的四桥臂三相逆变器[J]. 中国电机工程学报, 2008, 28(3):73-76.

WANG Huizhen, DING Yong, ZHANG Fanghua, et al. Four-leg three-phase inverter based on switching-node preset[J]. Preceedings of the CSEE, 2008, 28(3): 73-76.

[8] 张方华, 丁勇, 王慧贞, 等. 四桥臂三相逆变器的特定谐波消除控制[J]. 中国电机工程学报, 2007, 27(7): 83-87.

ZHANG Fanghua, DING Yong, WANG Huizhen, et al. The SHE control strategy on three-phase four-leg inverter[J]. Preceedings of the CSEE, 2007, 27(7): 83-87.

[9] 阮新波,严仰光. 四桥臂三相逆变器的控制策略[J]. 电工技术学报,2000,15(1): 61-64.

RUAN Xinbo, YAN Yangguang. The control strategy for three-phase inverter with four bridge legs[J]. Transactions of China Electrotechnical Society, 2000, 15(1): 61-64.

[10] 戴训江,晁勤. 一种新颖的并网逆变器自适应电流滞环控制策略[J]. 电力自动化设备,2009,29(9):85-89.

DAI Xunjiang,CHAO Qin. Adaptive current hysteresis control of grid-connected inverter[J]. Electric Power Automation Equipment,2009,29(9):85-89.

[11] 陈宏志, 刘秀翀. 四桥臂三相逆变器的解耦控制[J]. 中国电机工程学报, 2007, 27(19): 74-79.

CHEN Hongzhi, LIU Xiuchong. Decoupling control of three-phase four-legged inverter[J]. Preceedings of the CSEE, 2007, 27(19): 74-79.

[12] 刘秀翀, 张化光, 陈宏志. 四桥臂逆变器中第四桥臂的控制策略[J]. 中国电机工程学报, 2007, 27(33): 87-92.

LIU Xiuchong, ZHANG Huaguang, CHEN Hongzhi. Control strategy of the fourth leg in four-leg inverter[J]. Preceedings of the CSEE, 2007, 27(33): 87-92.

[13] 张晓勇,王军,李川，等. 基于三维空间矢量中Υ分量控制的三相四桥臂逆变器[J]. 电力自动化设备,2010,30(12):70-73.

ZHANG Xiaoyong,WANG Jun,LI Chuan et al. Three-phase four-leg inverter based on Υ component control in three-dimensional space vector[J]. Electric Power Automation Equipment,2010,30(12):70-73.

[14] 孙驰, 马伟明, 鲁军勇. 三相逆变器输出电压不平衡的产生机理分析及其矫正[J], 中国电机工程学报, 2006, 26(21): 57-64.

SUN Chi, MA Weiming, LU Junyong. Analysis of the unsymmetrical output voltage distortion mechanism of three-phase inverter and its correction[J]. Preceedings of the CSEE, 2006, 26(21): 57-64.

[15] 孙驰, 鲁军勇, 马伟明. 一种新的三相四桥臂逆变器控制方法[J]. 电工技术学报, 2007, 22(2): 57-63.

SUN Chi, LU Junyong, MA Weiming. A novel control method for three-phase four-leg inverter[J]. Transactions of China Electrotechnical Society, 2007, 22(2): 57-63.

[16] 孙驰, 毕增军, 魏光辉. 一种新颖的三相四桥臂逆变器解耦控制的建模与仿真[J]. 中国电机工程学报, 2004, 24(1): 124-130

SUN Chi, BI Zengjun, WEI Guanghui. Modeling and simulation of a three-phase four-leg inverter based on a novel decoupled control technique[J]. Preceedings of the CSEE, 2004, 24(1): 124-130

(编辑：刘素菊)

Control strategy of three-phase four-leg inverter using an auxiliary triangle waveform

MA Hai-xiao1, YE Hai-yun1, GONG Chun-ying2

(1.College of Automation Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210023, China；2. College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

The common control methods of Three-phase four-leg inverter are open loop control or need a lot of tedious calculation. These methods are not fit for medium-high frequency inverters, which require higher dynamic and static performance. In order to overcome these shortcomings, a control strategy of Three-Phase Four-Leg inverter using an auxiliary triangle waveform was proposed. This control strategy was based on voltage-current double closed loop control principle. Through establishing the voltage and current equations of Three-phase four-leg inverter and deriving the conditions of ensuring the symmetry of three-phase output voltages, the important roles of triangle waveform were found to control all the legs. In this strategy, the first three legs adopted voltage-current double closed loop control method with a triangle wave injection. The modulation ratio could be greater than one, so it can improve the utility ratio of DC voltage. The fourth leg adopted Pulse Width Modulation control method using a composed triangle wave as the modulation signal. The control of this leg ensured that three-phase output voltages were symmetrical when the inverter supply unbalanced loads. A 6kVA prototype was designed. The results of simulation and experiment proved the feasibility of this control strategy.

three-phase four-leg inverter； triangle waveform; double closed loop control; symmetrical component method; zero sequence harmonic

2014-11-11

国家自然科学基金(51107057)

马海啸(1980—), 男,博士,副教授,硕士生导师,研究方向为电力电子与电力传动;

马海啸

10.15938/j.emc.2016.01.003

TM 464

A

1007-449X(2016)01-0014-08

叶海云(1989—), 女,硕士研究生,研究方向为电力电子与电力传动;

龚春英(1965—), 女,博士,教授,博士生导师,研究方向为电力电子与电力传动。