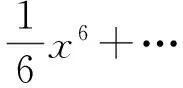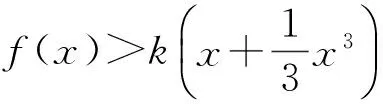2道高考题的共同背景和命题思路*
●余建国
(大厂高级中学 江苏南京 210044)
2道高考题的共同背景和命题思路*
●余建国
(大厂高级中学 江苏南京 210044)
源自课本的一个函数不等式,反映了指数(对数)函数与多项式函数的大小关系,它有很多的变形和拓展.循此思路,若干高考函数压轴题就是在指数(对数)函数的泰勒展开式的基础上“截取”多项式函数,并与其他有理函数组合,融入参数,将问题“倒过来”设问,编制而成.
数学高考;函数压轴题;泰勒展开;命题思路
每年的高考压轴题,我们在惊叹考题设计之精巧、解答之天衣无缝的同时往往很想知道“这些题从哪来,如何构造出这么精准的函数”.怀揣好奇之心,笔者对2015年的2道高考题仔细研究,发现原来如此!
例1 已知函数f(x)=ln(1+x),g(x)=kx,k∈R.
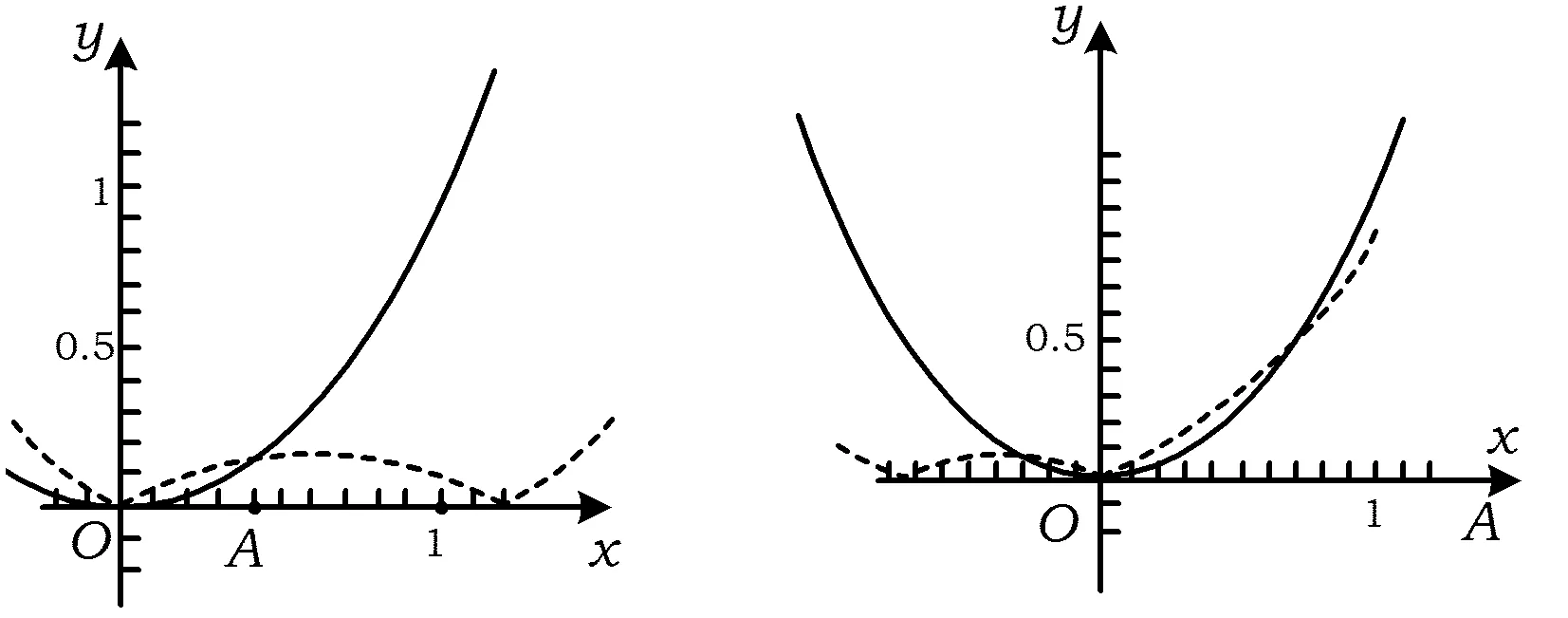
1)证明:当x>0时,f(x) 2)证明:当k<1时,存在x0>0,使得对任意的x∈(0,x0),恒有f(x)>g(x); 3)确定k的所有可能取值,使得存在t>0,对任意的x∈(0,t),恒有|f(x)-g(x)| (2015年福建省数学高考理科试题第20题) 第1)小题就是证明不等式:当x>0时,ln(1+x) 在图2中,将函数y=ln(1+x)在原点处的切线y=x绕原点旋转,于是当直线l:y=kx的斜率k∈(0,1)时,l必与函数y=ln(1+x)的图像在第一象限有一个交点(x0,f(x0)),因而当x∈(0,x0)时,根据图像位置关系恒有f(x)>g(x)(如图3所示).而当k≤0时,因为x∈(0,+∞),所以f(x)>0,g(x)<0,f(x)>g(x),x0的存在性是显然的,x0可以是任意正数.这样,第2)小题就“命题”成功了. 图1 图2 图3 如果说第1),2)小题还能从初等数学背景“还原”命题思路,那么第3)小题是如何产生的呢?我们不妨从《数学分析》中找一找:函数f(x)在x=0处的泰勒展开式为 (1) 因此,函数f(x)=ln(1+x)在x=0处的泰勒展开式为 (2) 或者用拉格朗日余项形式写成 其中0<θ<1,于是不等式|f(x)-g(x)| 由于0<θ<1,0 图4 图5 而当k=1时,由x>ln(1+x),可令 m(x)=x-ln(1+x)-x2= 因为0<θ<1,当x∈(0,+∞)时,m(x)<0,即 x-ln(1+x) 经过“参数化”,即|kx-ln(1+x)| 至此,第3)小题的命题思路已十分清楚:先将超越函数ex,lnx等用泰勒公式展开,这样就能“截取”多项式函数,并与其他有理函数组合;然后融入参数,并将问题“倒过来”编制.仿此思路,也来命制一题. 背景 函数f(x)=ln(1-x)在x=0处的泰勒展开式为 (3) 式(2)-式(3),得 当0 基于这个背景,仿例1的思路,现在我们也可以“成功”地编制出以下高考试题: 1)求曲线y=f(x)在点(0,f(0))处的切线方程; (2015年北京市数学高考理科试题第18题) 高考题并不神秘!作为一线教师,要摒弃题海战术,真正理解数学,在整个数学的历史长河中摸清经典试题的背景和来龙去脉,引导学生理解数学、解决问题,这样的复习对高考才是有效的. [1] 单墫.普通高中课程标准实验教科书·数学(选修2-2)[M].南京:江苏教育出版社,2012. [2] 毛丽娜,魏定波.一个指数函数不等式 五道高考数学压轴题[J].福建中学数学,2014(1/2):74-76. [3] 陈传璋.数学分析(上) [M].北京:人民教育出版社,1979. �2015-09-01; 2015-09-29. 余建国(1965-),男,江苏南京人,中学高级教师,研究方向:高中数学解题与课堂教学. O12 A 1003-6407(2016)03-49-021 初步分析

2 高数背景

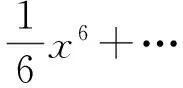

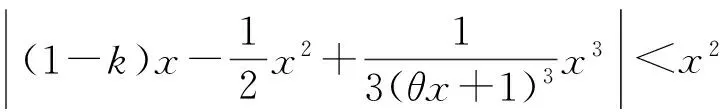
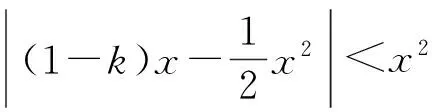
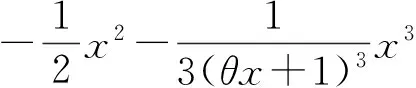
3 自由组合