3个几何不等式的统一指数推广*

●黄兆麟

(天津水运高级技工学校 天津 300456)



3个几何不等式的统一指数推广*

●黄兆麟

(天津水运高级技工学校 天津 300456)

文献[1-3]中的3个几何不等式虽然下界相同,但各自所给出的证明方法均不相同,无法统一.笔者通过定理4,不仅将3个几何不等式有机地联系在一起,而且还将其作了指数推广,充分揭示了3个几何不等式的本质联系,给人带来“既见树木,又见森林”的整体美感.

旁切圆半径；高线；角平分线；中线；几何不等式

文献[1]中利用3个引理证明了如下定理1:

定理1 设a,b,c是△ABC的3条边长,wa,wb,wc是△ABC的角平分线，则

而文献[2]指出仅用文献[1]中的引理1即可获证定理1,且文献[2]又将定理1加强为如下定理2.

定理2 设a,b,c是△ABC的3条边长,对应边上的中线为ma,mb,mc，则

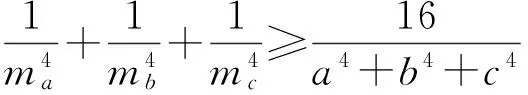
文献[3]又给出含旁切圆半径的类似不等式(定理3).

定理3 设a,b,c是△ABC的3条边长,ra,rb,rc为△ABC的旁切圆半径，则

文献[1-3]所用方法均不相同,让人“只见树木,不见森林”.为了更好地看清以上3个定理的本质及联系,本文特将以上3个定理统一指数推广为如下定理4.

定理4 设a,b,c是△ABC的3条边长,对应边上的旁切圆半径、高线、角平分线、中线长分别为ra,rb,rc;ha,hb,hc;wa,wb,wc;ma,mb,mc,指数p≥1,则

证明 首先证明当指数k>1,链中前3个不等式成立,即

(1)

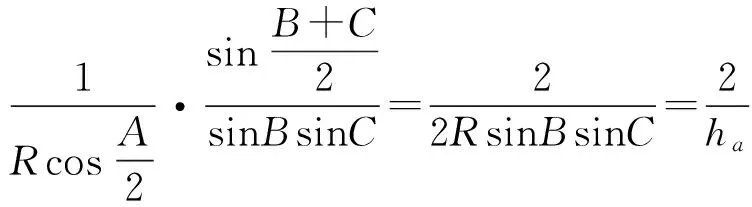
即

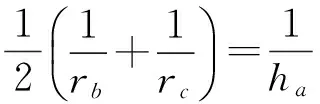
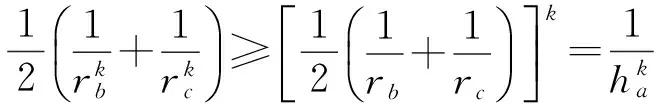
即

同理可得

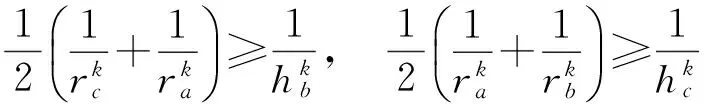
3个式子相加得

即链(1)中第1个不等式成立.当且仅当a=b=c时取等号.

再证链(1)中第2,3个不等式:

即

ma≥wa≥ha，

从而

于是

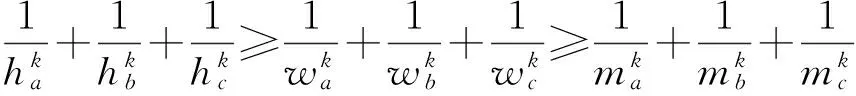
即链(1)中第2,3个不等式成立.当且仅当a=b=c时取等号.至此不等式链(1)全部获证.

在不等式链(1)中取k=2p(其中p≥1)即得定理4中不等式链的前3个不等式成立.

最后证明定理4中第4个不等式成立,即证如下不等式(2)成立:

(2)

即当p=1时不等式(2)成立.当p>1时,由幂平均不等式,可得

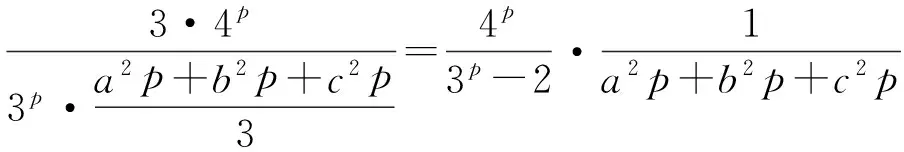
即当p>1时,不等式(2)也成立.综合可得当p≥1时定理4中第4个不等式成立.至此定理4全部获证.

[1] 曾善鹏.一个角平分线不等式[J].数学通报,2009(12):45.

[2] 安振平.一个角平分线不等式的简证与加强[J].数学通报,2011(4):38.

[3] 马占山,范红英.关于三角形旁切圆半径的一个有趣性质[J].数学通报,2011(11):57.

�2015-11-19；

2015-12-25.

黄兆麟(1961-)，男,湖南隆回人,高级讲师，研究方向：数学教育.

O122.3

A

1003-6407(2016)03-34-02