具有能级稳定过程的MQHOA优化算法
王鹏,黄焱
(1. 西南民族大学计算机科学与技术学院,四川 成都 610225;2. 淮阴师范学院计算机科学与技术学院,江苏 淮安 223300)
具有能级稳定过程的MQHOA优化算法
王鹏1,黄焱2
(1. 西南民族大学计算机科学与技术学院,四川 成都 610225;2. 淮阴师范学院计算机科学与技术学院,江苏 淮安 223300)
在量子模型下将优化问题转化为求解约束态的基态波函数问题,通过泰勒近似采用谐振子势阱对目标函数进行逼近,类比量子谐振子的波函数图像提出了一种改进的多尺度量子谐振子优化算法。算法包括3个基本迭代收敛过程:能级稳定过程、能级降低过程和尺度降低过程,算法的收敛过程与物理模型基本吻合。改进算法将主观控制参数减少为1个,同时参照量子模型定义了算法的波函数和零点能。实验结果表明,改进算法的复杂函数优化性能优于多种常见优化算法,对于Ackley、Griewank、Sphere、Sum Squares、Zakharov等高维标准测试函数均能以100%的概率获得全局最优解。
优化算法;函数优化;多尺度量子谐振子算法;波函数;基态
1 引言
利用自然现象和自然规律构造新的计算智能算法是一种常用的方法,如蚁群算法、遗传算法、粒子群算法、神经网络算法。但计算智能算法所面临的问题是大量算法缺少完整的数学理论基础,不能充分地利用数学工具对算法进行研究和分析,这一点制约了这一研究领域的发展。20世纪初量子物理打破了几百年来牛顿力学对世界确定性的描述,使人类认识到不确定性才是这个世界的本质,量子理论成熟完备的理论体系为算法的研究提供了方便,利用量子理论来构造和改进算法受到了大家的广泛重视。如量子退火算法(QA, quantum annealing)就是一种利用含时薛定谔方程的演化原理逐步向基态收敛,从而实现对全局最优解搜索的算法[1~4];文献[5~7]也提出了一种利用δ势阱波函数构造的量子粒子群(QPSO)算法,由于QPSO算法采用了δ势阱,所以收敛速度较快,但算法容易早熟,而且人为控制参数多,需要指定最大迭代次数实现对算法进行强行终止。以上算法都利用了量子波函数的概率解释,基于量子波函数构造的智能优化算法通常都是以向能级基态进化为目标,通过量子隧道效应避免陷入局部最优区域。
受到量子退火理论的启发,2013年,王鹏等[8]首次提出了多尺度量子谐振子算法(C-MQHOA)的基本物理模型和算法框架,C-MQHOA算法类比量子谐振子不同能级波函数构造了一个以多个正态采样为基本操作的多尺度采样搜索方法,利用多个正态采样的迭加作为算法波函数来描述当前最优解的概率分布,这一算法被成功应用于函数优化问题;文献[9]对 C-MQHOA算法的物理模型从经典谐振子和量子谐振子角度进行了分析,利用量子算符方法证明了优化算法的测不准关系,测不准关系从理论上指出了一般优化算法进行多尺度迭代的必要性;文献[10]给出了C-MQHOA算法的程序实现方法;文献[11]和文献[12]分别将 C-MQHOA算法成功应用于多峰函数和整数优化问题。文献[13]和文献[14]将C-MQHOA算法的基本思想应用于聚类分析和TSP组合优化问题,这意味着C-MQHOA算法有望在非函数优化领域,如数据中心优化[15]、集群调度[16]等实际工程问题中得到成功应用。但文献[8]所提出的C-MQHOA算法框架需要有2个主观控制参数,缺乏能级稳定过程,与物理模型存在不一致的地方,算法每次迭代需要对较多的位置进行采样,算法效率较低,不能实现对超高维复杂函数的优化。针对文献[8]中 C-MQHOA算法存在的问题,本文提了C-MQHOA算法的改进模型,引入了能级稳定过程,使新的MQHOA算法与物理模型符合的更好,在减少主观控制参数个数的同时实现了算法效率的大幅度提高,可以高效地求解超高维复杂函数的优化问题,因此,本文所提出的算法模型可以取代文献[8]中原有 C-MQHOA算法作为新的MQHOA算法的基本模型,因此,本文直接称新算法为MQHOA算法。
2 MQHOA算法的基本物理模型
量子理论的出现使人们认识到了一个由概率所统治的世界,大家所生活的世界并不是确定的。如图1所示,经典物理中按照卢瑟福的原子模型通常将电子的运动用确定的轨道来进行描述,但这一模型无法解释原子结构的稳定性,带电粒子做圆周运动时会辐射能量,按照这一模型电子将最终落入原子核中。量子力学的出现使人们对微观粒子的运动有了新的认识,依据量子力学理论原子核外电子的运动并没有确定的方向和轨迹,只能用电子云描述它在原子核外空间某处出现几率的大小,在量子力学中粒子出现的几率可以利用波函数(wave function)来进行描述,但波函数既不能描述粒子的轨迹也不能描述粒子的形状,对于任意粒子只能依据波函数给出其位置分布概率。

图1 经典电子轨道和量子电子云
描述量子系统的方程被称为薛定谔方程,它可以被写为如下的形式

定态薛定谔方程描述了粒子在势阱V( x)约束下的运动情况。MQHOA算法将优化问题中的目标函数f( x)作为薛定谔方程中的势阱 V( x) =f( x),函数优化问题在这一对应条件下就转变为了求粒子在势阱 V( x) =f( x)约束下的基态波函数ψ0(x)问题,量子系统处于基态时粒子将以最大的概率出现在势阱最低点附近,基态波函数的概率分布就是目标函数最优解的概率分布。但通常复杂的势阱利用薛定谔方程是无法求出精确波函数的。在量子物理中经常会采用谐振子势来近似描述粒子在平衡位置附近的复杂振动。同样,复杂目标函数f( x)在全局最小值位置x0附近也可以采用泰勒序列进行展开


在f( x)的泰勒展开中f( x0)为常数,在最小值位置x0处目标函数的一阶导数 f′(x0) = 0,同时去除高次项保留二次项,可以得到因此,在最小值位置x0附近,可以利用谐振子势阱来近似表示复杂目标函数f( x),在这一近似条件下求解目标函数f( x)最小值的问题就可以转变为求解在谐振子势阱约束下的基态波函数问题(谐振子约束态问题),此时薛定谔方程为
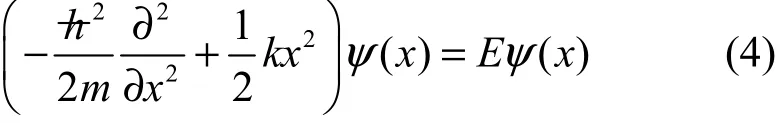
根据量子理论,谐振子势阱约束下的波函数是可以准确获得的,其不同能级波函数如图2所示。
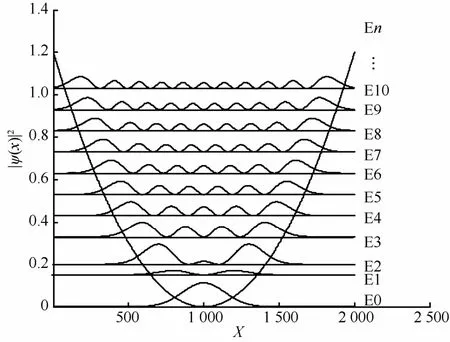
图2 不同能级下的谐振子波函数
量子谐振子波函数从高能态到基态由多个正态分布的概率振动逐步聚集到一起,其基态波函数就是一个正态分布,因此,MQHOA算法的基本采样概率函数为正态分布函数。本文引入了能级稳定过程,使MQHOA算法在高能级的亚稳态能进行充分的搜索,保证了解的多样性,从而更准确地定位所有局部最优区域。
MQHOA算法的物理模型可以归纳为以下几点。
1) 势阱等效:将复杂目标函数等效于量子势阱V( x) =f( x),从而将优化问题转化为求解约束态下量子基态波函数的问题。
2) 泰勒近似:在目标函数极值附近利用谐振子势对目标函数进行近似。
3) 量子波函数:利用波函数来描述目标函数最优解当前的概率分布。
4) 量子能级:目标函数的局部最优对应于量子系统中的高能级亚稳态,全局最优对应于量子系统中的基态。
在这一物理模型下优化问题就被转变为求解量子系统基态波函数的问题,利用量子退火方法实现系统由高能级亚稳态向基态的能级逐步跃迁。量子理论完整的数学体系为算法分析提供了数学工具。
3 MQHOA算法的基本迭代过程
根据算法的物理模型,本文提出了一种具有能级稳定过程的MQHOA算法流程,算法流程的伪代码如下(二维目标函数)。
MQHOA算法伪代码如下。
Initialize:k, σmin, σs=max −min
Randomly generate xi( i =1,… ,k) in domain[min,max]
Calculate the standard deviation σk′ for all xi
Do
Do
Do
∀xi, generate
∀xiandif f() Calculate the standard deviation σk While( ∆σk> σs) Update the worst solution xworst=xmean While (σk>σs) While(σs>σmin) Output xbestand f( xbest) 伪代码中目标函数的定义域为[min,max],算法的初始尺度 σs=max−min ,算法需要主观指定的参数只有采样区域个数k,k值越大对应于算法初始能级越高,而σmin则是优化算法在每一个维度上的收敛精度,MQHOA算法可以以指定的位置精度自动实现算法的收敛,也可人为指定最大迭代次数。算法初始化时在目标函数定义域内的每一个维度分别随机生成k个采样位置xi,并计算出这k个采样位置的标准差σk′。为描述方便,下面以二维函数为例说明算法包括3个迭代过程。 1) 能级稳定过程 这一迭代过程对所有的k个采样位置xi分别按正态分布 N( xi,)生成一个新的采样位置,总共生成k个新的采样位置,如果新采样位置对应目标函数的值较小 f() 2) 能级降低过程 当算法处于稳定能级状态后,以k个采样位置的平均值xmean=x替换x中最差解的位置 xworst,实 i i现了系统能级的下降并进入下一个低能级上的能级稳定过程。相比利用最优解位置取代最差解位置的能级降低策略,本策略保证了解空间采样的多样性。MQHOA算法的能级下降过程要一直持续到当前k个采样位置的标准差σk小于等于当前尺度σs( σk≤σs),这时k个采样位置xi收缩到了正态分布N( x,σ2)区域内,此时算法认为已达到尺度σ下 i ss 的能量基态,即最低能量状态。 3) 尺度降低过程 尺度降低过程与量子退火算法的退火过程类似,根据文献[9]中证明的优化算法测不准关系,要实现对全局最优解的高精度搜索必须采用多尺度迭代。尺度决定了搜索的精度,当算法达到尺度σs下的基态时,尺度降低过程将当前尺度减半使算法在更小的尺度下重复能级由高到低的迭代过程,从大尺度到小尺度的变化过程对应于算法逐步从全局搜索过渡到局部搜索,尺度减半的原理来自于小波二进变换的启发,按尺度减半在大多数目标函数上都表现出了良好的性能。最小搜索尺度σmin就决定了算法结果的位置精度,当前尺度σs≤σmin时,算法停止并输出xi中的最优结果。对于不同的目标函数只需指定σmin,MQHOA算法的迭代次数是不同的,算法可以自动适应并不需要人为指定。 MQHOA算法流程与物理模型的对应关系如表1所示,从表中可以看出MQHOA算法很好地符合了量子理论模型。 表1 MQHOA算法与物理模型的对应关系 MQHOA算法在整个搜索过程中其采样操作的核心机制就是当前k个采样位置xi所对应的k个正态概率分布 N( xi,,定义算法当前波函数为k个正态概率分布 N( xi)的叠加 高斯函数可以作为小波分析函数,受小波二进分析的启发,为实现更高分辨率的搜索,MQHOA算法将尺度σs逐步减半,尺度减小后算法在大尺度下的基态转变为在小尺度下的高能态,算法以更高的精度对解空间进行搜索,算法在最后结束时的波函数为 类比量子理论MQHOA算法的能量Esσ定义如下 当算法满足亚稳态判据时,此时的能量即为该亚稳态的能级。 依据能量Eσs的定义,MQHOA算法在尺度σs基态时的零点能可以近似由下式计算 其中,ψ0(x)为算法基态波函数,fmin为目标函数的理论最小值,f( xopt)是基态时当前的最优解。通常在当前尺度σs较大时零点能会较大。零点能的存在正是算法量子特性的一个重要表现,零点能也可作为算法收敛特性的指标。 为确保本文实验数据的可靠性,所有实验数据均为重复 30次计算所得到的统计值,测试函数如表2所示。本文MQHOA算法的参数k=30,算法的优化位置精度 σmin= 0.000 001,优化成功率的判断是以目标函数最终优化值与理论最优值差的绝对值小于等于0.001作为判断标准,优化目标函数的维度用D来标识,优化目标均是寻找目标函数的全局最小值,本文所有标准测试函数的理论最优值均为0。 表2 7种测试函数的名称与编号 表3给出了MQHOA算法对7种标准测试函数在10维和30维时的优化结果,搜索定义域在各个维度均为[-2.048, 2.048]。对这7种标准测试函数,除f2函数之外,MQHOA算法均以较高的精度获得了全局最优值。其函数进化次数通常只需要103~104次,并且随维度的增加变化不明显,这表明算法迭代次数对于目标函数的维度并不敏感,可以应用于高维函数的优化问题。在本次实验中除f2函数之外,其余测试函数MQHOA算法在30次重复实验中都以100%的概率找到了全局最优值。 表4中的数据为MQHOA算法与其他3种常见优化算法 ABC(artificial bee colony algorithm)、JDE(differential evolution algorithm)、CLPSO(comprehensive learning PSO)对5种100维的标准测试函数 30次重复实验中获得的全局最优值的平均值。实验结果表明,MQHOA算法的实验结果全部优于CLPSO算法,对4种测试函数(f3, f5, f6, f7)的实验结果优于ABC、JDE算法;对比算法对函数f7的实验结果从精度上看可以认为 ABC、JDE、CLPSO算法在30次实验中并未能有效地找到最优解位置,事实上其成功率为0,而MQHOA算法却以10-8的精度找到了全局最优解。如果以0.001为标准,MQHOA在30次实验中共找到了4种函数(f3, f5, f6, f7)的全局最优解位置,优于其他3种对比算法。 在函数优化问题中随着目标函数维度的增加,搜索空间的大小是呈指数级增长的,因此,优化算法对高维目标函数特别是百维以上的超高维目标函数的优化性能是优化算法的一个重要评价指标。 表3 MQHOA算法对7种常见目标函数的优化结果 表4 MQHOA与其他算法对高维目标函数的优化效果对比 表5为MQHOA算法对5个200~500维的超高维目标函数优化的结果,搜索定义域在各个维度均为[-2.048, 2.048],数据表明MQHOA算法在目标函数为200~500维时,仍以100%的成功率获得了目标函数的全局最优解。总的来看,MQHOA算法具有出色的高维函数优化能力,这表明其有望应用于高复杂度的优化应用领域,是一个有很好应用前景的智能优化算法。 根据本文对算法波函数的定义,波函数是MQHOA算法量子特性的重要体现,它反映了当前目标函数全局最优解的概率分布,算法的收敛过程也是波函数在不同尺度向基态收敛的过程。 表5 MQHOA对超高维目标函数的优化实验结果 图3为MQHOA算法在对Griewank函数进行优化时,在不同尺度下( σs=10,σs=5,σs=1.25)收敛到基态时的波函数图像。图中的圆点为波函数对应的k个采样中心的位置,从图中可以看出随着尺度的降低算法波函数逐步向目标函数的全局最优位置聚集,波函数的这种聚集同时会使算法的采样概率集中在全局最优位置,从而提高最优解附近的采样密度。从图中可以直观地看出由于波函数的概率特性,算法在大尺度时可以实现对定义域的全局搜索,而在相对小的尺度下也能以一定的概率跳出局部最优区域,这在量子理论中被称为量子隧道效应。波函数反映了算法当前全局最优解的概率分布,也是算法当前的采样概率分布。 图3 Griewank 函数在不同尺度下的采样中心及基态波函数图像(D=2) 本文引入能级稳定过程提出了一种改进的MQHOA算法模型,新的模型包括能级稳定过程、能级降低过程和尺度降低过程3个迭代过程,新的MQHOA算法实现了对超高维复杂函数优化问题的快速求解,算法结构简单、实现容易。相比同类优化算法,MQHOA算法的迭代过程具有简单明确的数学过程,整个算法的基本操作只有正态采样和 3个收敛判据,这种简单明确的数学结构特别有利于对其进行收敛性分析。同时MQHOA算法需要主观设定的控制参数只有采样区域个数k,避免了多个控制参数所造成的算法参数设定时的困难。实验证明具有能级稳定过程的 MQHOA算法在对高维函数的优化中比其他算法具有明显的优势。今后具有能级稳定过程的MQHOA算法将作为MQHOA算法的基本算法对待。由于本文所提出的具有能级稳定过程的 MQHOA优化算法有着清晰完整的物理模型描述,目前已非常成熟的量子理论的数学体系为研究这一算法提供了强大的数学工具,解决了其他计算智能算法缺乏完备数学体系的问题。 [1] BATTAGLIA D A, SANTORO G E, TOSATTI E. Optimization by quantum annealing: lessons from hard satisfiability problems[J].Physical Review E Statistical Nonlinear & Soft Matter Physics, 2005,71(6): 531-536. [2] FINNILA A B, GOMEZ M A, SEBENIK C, et al. Quantum annealing:a new method for minimizing multidimensional functions[J]. Chem Phys Lett, 1994, 219 (5-6): 343-348. [3] SOMMA R D, BOIXO S, BARNUM H, et al. Quantum simulations of classical annealing processes[J]. Phys Rev Lett, 2008, 101(13): 130504.[4] BROOKE J, BITKO D, ROSENBAUM T F, et al. Quantum annealing of a disordered spin system[J]. Science, 2001, 284(5415): 779-781. [5] SUN J, WU X J, VASILE P, et al. Convergence analysis and improvements of quantum-behaved particle swarm optimization[J]. Information Sciences, 2012, 193(15): 81-103. [6] FENG B, SUN J, XU W B. A global search strategy of quantum-behaved particle swarm optimization[C]//Proc of IEEE Conference on Cybernetics and Intelligent Systems, c2005: 111-116. [7] SUN J, FANG W, WU X J, et al. Quantum-behaved particle swarm optimization: analysis of the individual particle behavior and parameter selection[J]. Evolutionary Computation, 2012, 20(3): 349-393. [8] 王鹏, 黄焱, 任超, 等. 多尺度量子谐振子高维函数全局优化算法[J].电子学报, 2013, 41(12): 2468-2473.WANG P, HUANG Y, REN C, et al. Multi-scale quantum harmonic oscillator for high-dimensional function global optimization algorithm[J].Acta Electronica Sinica, 2013, 41(12): 2468-2473. [9] 王鹏, 黄焱. 多尺度量子谐振子优化算法物理模型[J]. 计算机研究与探索, 2015, 9(10): 1271-1280.WANG P, HUANG Y. Physical model of multi-scale quantum harmonic oscillator optimization algorithm[J]. Journal of Frontiers of Computer Science & Technology, 2015, 9(10): 1271-1280. [10] 刘峰, 王鹏, 黄焱, 等. 多尺度量子谐振子优化算法实现方法研究[J].成都信息工程学院学报, 2015, 30(5): 433-438.LIU F, WANG P, HUANG Y, et al. Research on algorithm implementation of multi-scale quantum harmonic oscillator algorithm[J]. Journal of Chengdu University of Information Technology, 2015, 30(5): 433-438. [11] 陆志军, 安俊秀, 王鹏. 基于划分的多尺度量子谐振子算法多峰优化[J]. 自动化学报, 2016, 42(2): 235-245.LU Z J, AN J X, WANG P. Partition-based MQHOA for multimodal optimization[J]. Acta Automatica Sinica, 2016, 42(2): 235-245. [12] 袁亚男, 王鹏, 刘峰. 多尺度量子谐振子算法性能分析[J]. 计算机应用, 2015, 35(6): 1600-1604.YUN Y N, WANG P, LIU F. Performance analysis of multi-scale quantum harmonic oscillator algorithm[J]. Journal of Computer Applications, 2015, 35(6): 1600-1604. [13] 燕京京, 王鹏, 范家兵, 等. 基于量子谐振子模型的聚类中心选取算法[J]. 电子学报, 2016, 44(2): 405-412.YAN J J, WANG P, FAN J B, et al. Clustering center selecting algorithm based on quantum harmonic oscillator model[J]. Acta Electronica Sinica, 2016, 44(2): 405-412. [14] 王鹏, 黄焱, 安俊秀, 等. 多尺度量子谐振子算法在组合优化问题中的性能分析[J]. 电子科技大学学报, 2016, 45(3): 469-474.WANG P, HUANG Y, AN J X, et al. MQHOA used in TSP problem[J].Journal of University of Electronic Science and Technology of China,2016, 45(3): 469-474. [15] 黄焱, 王鹏, 谢高辉. 基于 PE方法的数据中心需量费用优化算法[J].通信学报, 2016, 37(3): 90-97.HUANG Y, WANG P, XIE G H. Optimizing demand charge of data center base on PE method[J]. Journal on Communications, 2016, 37(3):90-97. [16] 王鹏, 黄焱, 李坤, 等. 云计算集群相空间负载均衡度优先调度算法研究[J]. 计算机研究与发展, 2014, 51(5): 1095-1107.WANG P, HUANG Y, LI K, et al. Load balancing degree first algorithm on phase space for cloud computing cluster[J]. Computer Research and Development, 2014, 51(5): 1095-1107. [17] CHEN D B, ZOU F, LI Z, et al. An improved teaching-learning-based optimization algorithm for solving global optimization problem[J].Information Sciences, 297(2015): 171-190. MQHOA algorithm with energy level stabilizing process WANG Peng1, HUANG Yan2 An improved multi-scale quantum harmonic oscillator algorithm (MQHOA) with energy level stabilizing process was proposed analogizing to quantum harmonic oscillator’s wave function. Inspired by quantum model, the optimization problem was transformed to finding ground state wave function of bound state. Harmonic oscillator potential well was used to approach objective function under the condition of Taylor approximation. Energy level stabilization, energy level reduction, scale reduction were the basic iterative convergence processes of MQHOA, coinciding with its physical model. Only one subjective control parameter was needed in MQHOA whose wave function and zero-point energy were defined with reference to quantum model. Experimental results show that MQHOA’s performance is superior to several other common optimization algorithms. For high dimensional testing functions including Ackley、Griewank、Sphere、Sum Squares、Zakharov, etc, the global optimums can be obtained precisely with 100% probability. optimization algorithm, function optimization, MQHOA, wave function, ground state s: The National Natural Science Foundation of China (No.60702075), Sichuan Key Laboratory Open Foundation of Pattern Recognition and Intelligent Information Processing (No.MSSB-2015-9) TP301.6 A 10.11959/j.issn.1000-436x.2016136 2016-04-11; 2016-06-15 国家自然科学基金资助项目(No.60702075);模式识别与智能信息处理四川省高校重点实验室开放基金资助项目(No.MSSB-2015-9) 王鹏(1975-),男,四川乐山人,西南民族大学教授、博士生导师,主要研究方向为智能算法、大数据、云计算、并行计算。 黄焱(1982-),男,江苏泗阳人,博士,淮阴师范学院讲师,主要研究方向为智能算法、并行计算。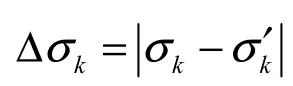

4 MQHOA算法的波函数和能量
4.1 MQHOA算法的波函数定义
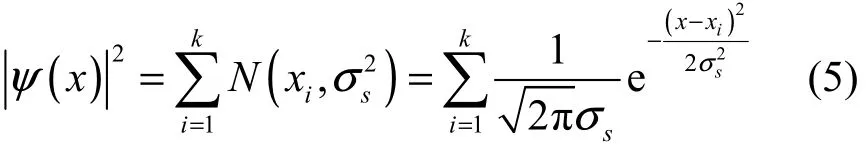

4.2 MQHOA算法的能量和零点能
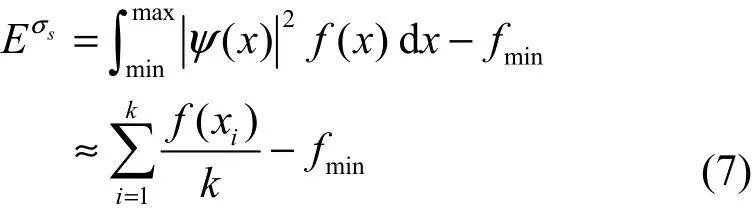
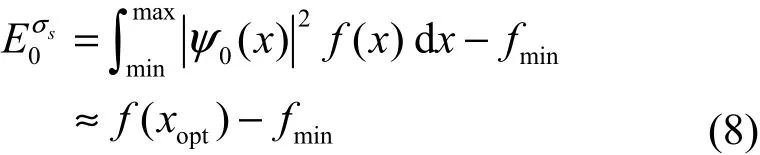
5 实验结果与讨论

5.1 MQHOA算法基本优化实验结果
5.2 MQHOA算法与其他算法的对比实验结果
5.3 MQHOA算法对高维函数的优化实验结果


5.4 MQHOA算法的波函数


6 结束语
(1. School of Computer Science and Technology, Southwest University for Nationalities, Chengdu 610225, China;2. School of Computer Science and Technology, Huaiyin Normal University, Huaian 223300, China)


