浅析万有引力定律及其在高中物理中的应用
王风尘
【摘 要】本文从万有引力定律的形成、万有引力定律与重力的关系以及其在航空航天方面的应用。分析在高中教授引力一章内容时遇到一些难点,以及如何突破。
【关键词】万有引力定律;高中物理;应用
一、万有引力定律的形成过程
站在巨人肩上的牛顿对伽利略、笛卡尔、会更斯、胡克、哥白尼、开普勒等人的科学研究以及在科研过程中体现的思想加以总结以及进一步总结、阐释,最终在经典物理学方面做出了杰出的成就。《自然哲学之数学原理》(以下简称《原理》)在物理学、方法论方面对人类社会的影响之深远难以估量。书中提出三大运动定律以及万有引力定律的内容及其证明,自此科学而又系统的经典物理学在人类的工业进程、文明进程中占据了重要的地位。纵观牛顿研究引力的整个过程,主要涉及两个难点:平方反比定律和引力质量与惯性质量的统一。
(1)平方反比定律。牛顿之前,引力平方反比的思想已经出现,胡克很早就认识到圆轨道运行时的平方反比定律,然而开普勒于1609年出版的《新天文学》中发表了两条行星运动的定律,其中第一条即椭圆轨道定律。科学家们一直以来对椭圆轨道中的平方反比定律都无法给与有效的证明,最后牛顿利用微积分的知识证明出在椭圆轨道中的引力平方反比定律,即。
(2)引力质量与惯性质量。牛顿的万有引力定律中提出引力F与两个相互吸引的物体的质量的乘积M·m成正比,即F∝M·m。其中M和m表示的是物体的引力质量。伽利略在研究落体运动时,结合自己的理想斜面实验,提出当没有任何阻力的情况下,物体在平直的桌面上会一直匀速运动或静止。这就是我们熟知的惯性,而且惯性与质量有关。从这里引出了惯性质量。如果将万有引力与做椭圆轨道运动的物体和地面上物体受到的重力联系起来,就必须承认惯性质量与引力质量相等。
(3)万有引力定律形成。万有引力定律是牛顿力学体系和天体运动的基石。万有引力告诉我们任何两个物体之间都存在的引力,然而高中教学时许多学生会有疑问:人教课标版的物理教材中提出,这个公式只适用于两个质点之间的计算,却又提到任意两个物体之间都存在引力。如果两个物体之间的距离远远大于自身的尺寸,两物体就可以看做质点,所以可以直接利用万有引力定律计算。一旦两个物体或其中一个无法看做质点时,针对质量分布均匀的球体可以认为它的质量集中于球心处,这种情况也可以利用万有引力定律直接计算。其实万有引力定律是牛顿通过微积分推导出来的,不过由于在高中无法利用微积分进行繁琐的计算,因此如果两个物体无法看成质点或者规则的球体则无法进行计算。牛顿的万有引力定律提出后,理论的正确与否,无疑需要经过大量的事实来验证。牛顿在《原理》中利用自己的万有引力定律解释了潮汐现象,他认为是地球与月球的吸引才出现这种状况;1843年,亚当斯计算出影响天王星运动的第八颗行星轨道,1846年,法国天文学家勒维耶,独立完成海王星位置的推算。同年,9月23日,海王星被发现,与勒维耶预测的位置相距不到1°;哈雷彗星的按时回归等等。天文学上多次重大发现,无不体现了牛顿万有引力定律的正确性。自此这个年轻的学科在人类世界中拥有了强大的生命力改变了人类的文明进程。
经典力学的基础是牛顿三大运动定律,万有引力定律更是建立了人们对牛顿物理的尊敬。牛顿运动定律和万有引力定律在宏观、低速、弱引力的广阔领域,包括天体力学的研究汇总,经受了实践的检验,取得了巨大的成就。人们基于万有引力不断的进行着科学探索,其中对重力的研究、对航空航天的探索,都在证实着万有引力定律的强大生命力。
二、引力与重力的关系
引力和重力都是两个物体之间的吸引,他们之间既有区别也有联系。
(1)重力与万有引力定律的定义。万有引力中的定义中指出任何两个物体之间都存在引力的作用。它的定义式告诉我们万有引力的大小与两个相互吸引的物体的质量的乘积成正比,与它们之间的距离的平方成反比。重力是由于地球对地球表面附近的物体的吸引而产生的。从定义上我们可以看出万有引力与重力有着一定的区别。
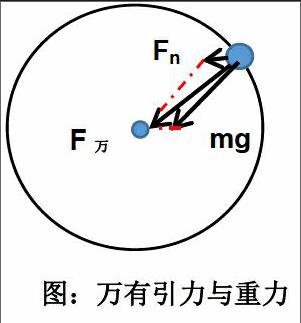
(2)地球表面处的万有引力与重力。如果把地球看做质量均匀分布的球体,地球的质量即可以认为集中到地心处,即质心在球心处。地面上的物体由于尺寸较小因此可以看做质点。万有引力的方向指向地心。地球自转的影响,导致万有引力的一个分力需要提供向心力,则另外一个分力就是重力。这种说法是高中物理教学时所用到的方法。向心力是根据力的作用效果来命名的一种力,而重力是性质力。笔者认为按照这种方法教学会给学生带来一定的误区,部分学生会记忆成万有引力可以分解为重力和向心力。高等物理教材中使用惯性离心力来代替万有引力所需要提供的向心力。
如图(万有引力与重力),设物体的质量m=1Kg万有引力F万与赤道平面的夹角为β,所以β 代表的就是纬度。重力mg与万有引力的夹角为α。在赤道处物体所需要的向心力,其中地球自转周期T=24h,地球半径吧r=6400km。处于赤道处的该物体所需要的向心力为0.034 N << 9.8 N,如果物体在北极向心力为零。物体所需要的向心力远小于万有引力,因此高中阶段的计算一般认为地球表面处的重力等与万有引力,α≈0。令F万=mg0,利用余弦定理(mω2Rcosβ)三、万有引力与航天
牛顿曾经提出过自己的关于宇宙航行的设想。根据万有引力定律计算出:如果想要发射一颗绕地球转动的卫星需要至少拥有7.9km/s的发射速度。当然开始的时候动力是制约卫星或者宇宙飞船能否顺利达到预定轨道的重要因素。随着导弹等技术的不断发展以及苏联科学家齐奥尔科夫提出了多级火箭的设想之后,经过了全国各界人士的协同合作、大量尝试后,苏联率先发射了自己的第一颗卫星、加加林少校成功坐上宇宙飞船绕地球航行。想要成功发射绕地飞行器,发射时需要达到第一宇宙速度。第一宇宙速度的计算在高中阶段涉及两种方法,其一、万有引力提供向心力:;其二,地球表面处的重力与万有引力近似相等(设地球半径是R)。通过这两种方法都可以顺利的得到第一宇宙速度。第一种方法,当r=R时,第一宇宙速度。由第二种方法得到结果是。经过计算两种方法的结果是一样的。不过第二以及第三宇宙速度的推倒需要用到动能与引力势能的转化,高中阶段不作要求。
四、结束语
牛顿的一生是辉煌的、传奇的,也是坎坷的一生。不论在生活中的困难有多大,但牛顿如孩童般的求知欲望始终留存。牛顿认为自己不过是在海边拾贝的一个孩子而已。从万有引力定律的形成过程,可以看出一个伟大的定律是如何一步步被推出的。牛顿解决重难题并不是一蹴而就的,而是通过长期的思考以及交流才得以完成。高中阶段在理论教学的基础上,结合史实应该进行引力形成过程的讲解。从引力在高中阶段的应用,我们发现高中阶段已经涉及到一个定律的核心思想。高中阶段对科学思想、科研方法的培养从万有引力定律的教学已经有所体现。因此引力的教学教给学生的不仅仅是知识点的理解,也有价值观上的熏陶。
参考文献:
[1]漆安慎,杜蝉英.《普通物理学教程(第二版)》.北京:高等教育出版社,2005.190-191

