双线性变换原理的多角度比较分析*
谢小娟,张爱清,冯友宏
(安徽师范大学物理与电子信息学院,安徽 芜湖 241000)
双线性变换原理的多角度比较分析*
谢小娟,张爱清,冯友宏
(安徽师范大学物理与电子信息学院,安徽 芜湖 241000)
从三个不同的角度对双线性变换式引出进行了推导,首先是从表征系统的差分方程和微分方程近似的角度,其次从解决脉冲响应不变法的频谱混叠问题的角度,最后是对z=esT的数学近似的角度。分析比较发现,从解决脉冲响应不变法的频谱混叠问题的角度来分析逻辑性最强,教与学的效果会更好。
数字滤波器;双线性变换;原理推导
数字滤波是数字信号处理的基本手段之一。在IIR数字滤波器的设计中,如果没有强调特殊要求,一般采用双线性变换法进行连续传递函数Ha(s)和离散传递函数H(z)的映射[1,2],即:
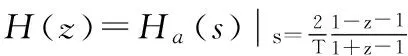
(1)
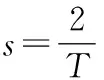
1 差分方程和微分方程近似的角度[3]
双线性变换法基本思想可以用表征数字滤波器H(z)的差分方程作为模拟滤波器H(s)所对应的微分方程的近似解(采用梯形近似积分),如果模拟传递函数H(s)可展开成部分分式之和:
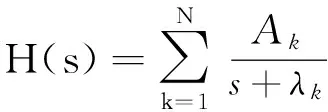
由于各项具有相同的形式,研究其中一项就足以说明整体的规律。每一项对应一个一阶微分系统
y′(t)+λy(t)=Ax(t).
(1)
对上式取拉氏变换,得模拟系统函数
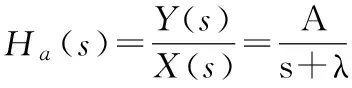
(2)
在一个抽样间隔(n-1)T→nT中对(1)式积分:
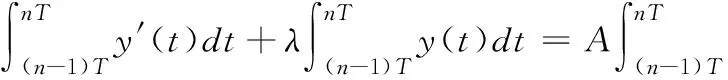
用梯形面积代替曲线积分,上式变为:
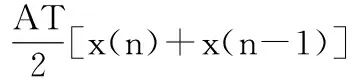
两边取z变换,整理得:
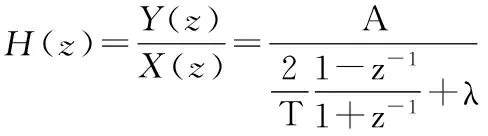
(3)
比较Ha(s)和H(z)的表达式(2)和(3),得:
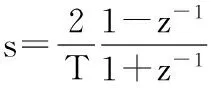
2 克服脉冲响应不变法缺点的角度
脉冲响应不变法实现模拟滤波器的数字化,其基本原理是从时域出发,假定模拟系统的单位冲激响应为h(t),而数字滤波器的单位脉冲响应为h(n),满足:
h(n)=h(t)|t=nT.
由此可以导出模拟滤波器系统函数Ha(s)与数字滤波器系统函数H(z)之间的映射关系为:
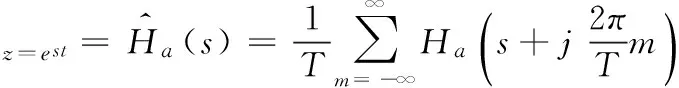
(4)
假定模拟滤波器是频率带限的或者高频衰减很大的情况下,则有:
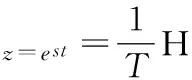
(5)
即模拟滤波器在满足严格带限的条件下,此时s与z是一一对应的关系,Ha(s)可以通过z=esT的映射关系直接得到H(z)。而双线性变换法,本质上也是一种从Ha(s)到H(z)的映射,那么关键就是找出一种s=f(z)的映射关系,既要满足数字化的两个基本要求即频响一致性和稳定性一致性,同时又能保证Ha(s)即使在不满足严格带限的条件下也能够通过s=f(z)的一一对应关系映射到H(z)。而双线性变换法通过引入中间变量s1并结合z=esT的映射关系,成功找到了满足上述要求的变换式,即双线性变式。具体实现是首先经过s到s1平面压缩,将不带限的Ha(s)压缩成了严格带限的Ha(s1),其次对Ha(s1)按照脉冲响应不变法数字化,则满足(2)式的条件,此时可将这个严格带限的Ha(s1)通过z=esT直接映射成H(z)。其理由是由于Ha(s1)是严格带限的,因此如果在s1平面进行采样后得到的采样信号的拉式变换Ha′(s1)是不会发生混叠的,因此可以直接让Ha(s1)通过z=es1T转换成H(z)。它和让Ha′(s1)通过z=es1T转换为H(z)在一个周期内是完全相等的,因此,我们可以直接让Ha′(s1)通过z=es1T转换成H(z)。最后综合s到z的映射,即为双线性变换式[4]。
3 对z=esT数学近似的角度[5]
根据脉冲响应不变法实现数字化,模拟滤波器系统函数Ha(s)与数字滤波器系统函数H(z)之间的映射关系满足(4)式。此外也可以由z变换的定义的引出,即借助抽样信号的拉式变换引出z变换定义,都可得到s与z满足z=esT的标准映射关系。
假定采样周期T足够小的情况下,利用级数展开可得:
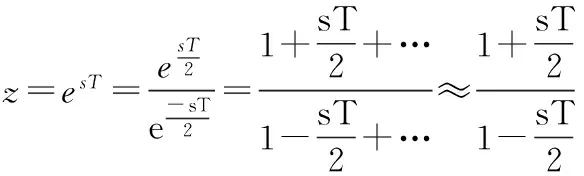
忽略高阶项,则可得双线性变换式为:
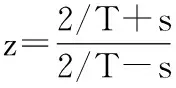
也可以从数值积分的梯形法对应得到。设积分器为:
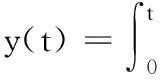
两边求拉式变换后可推导出积分器系统函数为:
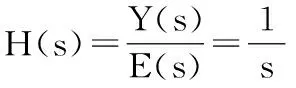
当用梯形法求积分运算可得算式如下:
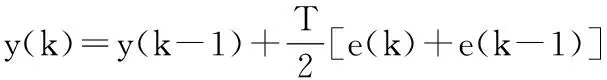
两边z变换后可推导出数字积分器为:
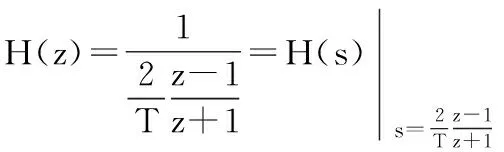
4 结论
通过比较分析,从脉冲响应不变法的角度推导双变换式,相比较其它两种推导方法在原理上稍显复杂,但它却具有以下三方面的突出优点。首先推导过程与脉冲响应不变法联系紧密,在教和学上承上启下,逻辑性强,便于学生理解掌握。其次可以很自然地从原理上得出其优缺点。优点是由于s平面到s1平面的压缩可以有效克服脉冲响应不变法之频谱混叠问题,缺点是s平面到s1平面的压缩会导致的模拟频率与数字频率之间的非线性关系,进而使得DF较AF频响会出现失真变形。最后可以自然地得出其应用场合和改善方法,即只有当失真是允许的或能被补偿时,才能采用双线性变换。如对于分段常数的滤波器,双线性变换后,仍得到幅频特性为分段常数的滤波器,但是各个分段边缘的临界频率点产生了畸变,这种频率的畸变可以通过频率的预畸来加以校正。综合来看,在数字信号处理课程中关于双线性变换化的教学,应重点采用从脉冲响应不变法的角度进行推导,如学时允许,可适当了解其两种方法为宜。
[1] 王世一.数字信号处理(修订版)[M].北京:北京理工大学出版社,2006.
[2] 吴镇扬.数字信号处理的原理与实现[M].南京:东南大学出版社,1999.
[3] 童晓兵,张玉明,徐以涛.“数字信号处理”课程中双线性变换法的探讨[J].电气电子教学学报,2014,36(2):68-70.
[4] 刘姝延,马秋明,吴志,等.用双线性变换法设计IIR数字滤波器[J].商丘师范学院学报,2005,21(5):26-29.
[5] 于海生,丁军航.微型计算机控制技术[M].北京:清华大学出版社,2009.
Multi Angle Comparative Analysis of the Principle of Bilinear Transformation
Xie Xiaojuan,Zhang Aiqing,Feng Youhong
(AcademicofPhysicsandElectricityInformation,AnhuiNormalUniversity,WuhuAnhui241000,China)
In this paper,the derivation of bilinear transformation is derived from three different perspectives.The first is from the point of view of differential equation and differential equation,the second is from the solution for the problem of frequency spectrum aliasing of the impulse response,and the last is from the view of the mathematical approximation of z=esT.By comparative analysis,the second one is with the strongest logic and is better for teaching and learning.
digital filter; bilinear transformation; principle derivation
2016-07-11
国家自然科学基金(No.61401004)网络多媒体流QoS特征稀疏表示及柔性跨域映射方法研究。
谢小娟(1982-),女,广西桂林人,讲师,硕士研究生,研究方向:信号处理。
1674-4578(2016)05-0029-02
TN713+.7
A

