一类耦合粘弹性波动方程解的有限时间爆破

董 莉,刘玉龙

(山西大学 数学科学学院，山西 太原 030006)



一类耦合粘弹性波动方程解的有限时间爆破

董 莉,刘玉龙

(山西大学 数学科学学院，山西 太原 030006)

研究一类带有强阻尼项和频散项的耦合粘弹性波动方程的初边值问题，利用凸性分析法，证明了当初值和松弛函数满足一定条件时,该方程的解在有限时间内爆破。

粘弹性；耦合波动方程；初边值问题；爆破

0 引言

在本文中，考虑如下耦合粘弹性波动方程的初边值问题：

这里Ω∈Rn是具有光滑边界∂Ω的有界区域。g和h是给定的函数，u0(x)，u1(x)，v0(x)和v1(x)是已知的初值函数，且

近年来，关于粘弹性波动方程解的研究吸引了众多学者的关注。Messaoudi[1]研究了带有非线性阻尼项的波动方程

(2)

当x∈Ω时的初边值问题，证明了p>m时在负初能量条件下解的爆破性和m≥p时解的存在性。之后，Messaoudi[2]和Wu[3]用两种不同的方法研究了方程(2)在正初能量条件下解的爆破性。2015年，宋海涛[4]进一步证明了在任意高的初能量下解的爆破结果。Cavalcanti[5]和Tatar[6,7]分析了具有强阻尼项和频散项的方程

在x∈Ω时解的整体存在性和指数衰减性。Wu[8]在文献[6]的基础上研究了非线性方程

的衰减性。Xu[9]在此基础上引入强阻尼项，并依据势井理论证明了方程

(3)

不变集和弱解的全局存在性，并且得出在任意高的初能量条件下，解在有限时间内爆破。随后Mohammad[10]将方程(3)由有界区域推广到全空间，研究了在负初能量条件下解的爆破结果。本文主要研究方程(3)的耦合方程组解的爆破性，不同于文献[9]和[10]的地方在于引入了多个函数，且在考虑若弱局部解、定义辅助函数和求能量函数时变得更复杂。

1 预备知识

为了证明本文的主要结果，首先给出一些数学符号、假设和重要引理.

用Lp(Ω)(1≤p<∞)表示所有定义在Ω上的泛函构成的一般空间，范数‖u‖p=‖u‖LP(Ω)。

假设：G1：g，h是R+→R+的可微函数，且

引理1[11]对于

有 uf1(u+v)+vf2(u+v)=pF(u,v)。

且存在正常数d0，d1，使得

引理2[12]假设ψ(t)∈C2(R)，满足

其中，常数C0>0，α>0，则ψ(t)在有限时间内爆破。

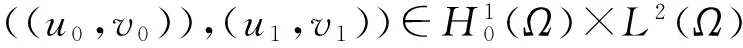
且

在这里，我们记能量函数为：

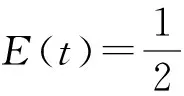
(4)

其中

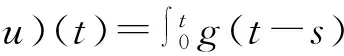
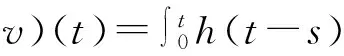
2 解的爆破

下面给出本文的主要结果。

定理2 假设G1成立，松弛函数g和h满足

且对任意的初值

满足

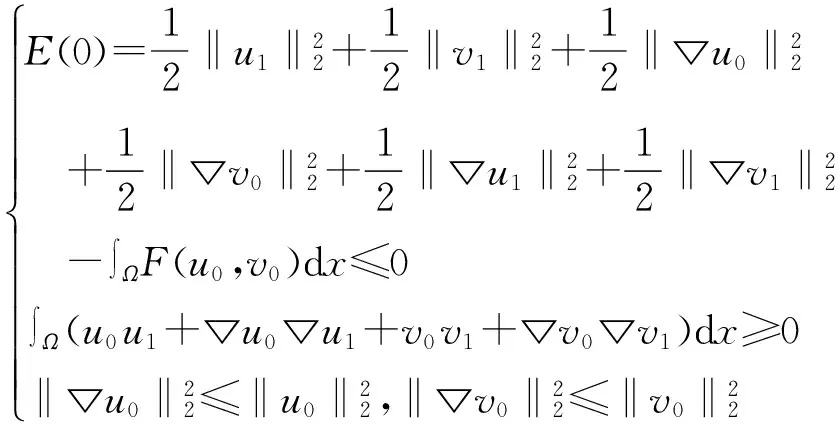
(5)

则方程(1)的解在有限时间内爆破。

证明 在(1)式的第1、2个方程两边分别同乘ut和vt，并关于x在Ω上积分，利用格林公式和分部积分可得

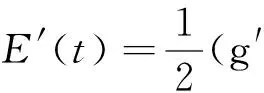
显然，E′(t)≤0，所以E(t)是单调递减的，则有E(t)≤E(0)≤0。

定义辅助函数：

关于t求导得

ψ′(t)=∫Ω(uut+▽u▽ut+vvt+▽v▽vt)dx

(6)

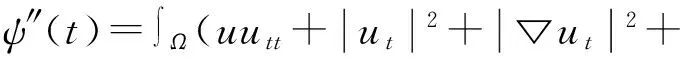
(7)

由(5)式可知ψ(0)>0，ψ′(0)≥0。

在(1)式的第1、2个方程两边分别同乘u和v，然后关于x在Ω上积分，利用格林公式得，

∫Ωuuttdx+∫Ω▽u▽uttdx+∫Ωvvttdx+∫Ω▽v▽vttdx

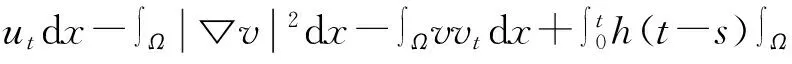
∫Ω▽v▽vtdx+∫Ω(f1u+f2v)dx

(8)

对等式右边第3项和第7项化变形得

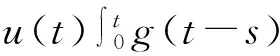
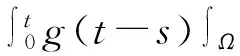
(9)

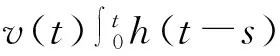
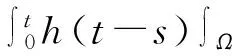
(10)

把(9)、(10)式代入(8)，再结合(6)、(7)式可得

ψ″(t)+ψ′(t)

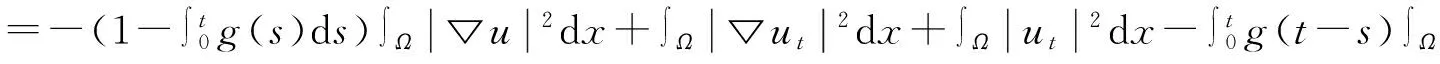
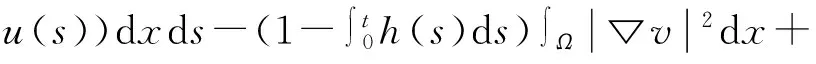
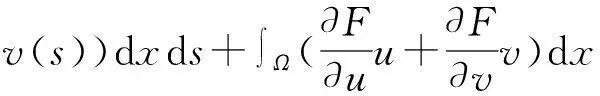
(11)

利用Young不等式对第2项和第4项化简

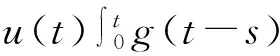
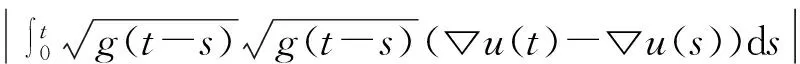
同理可得

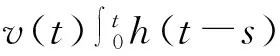
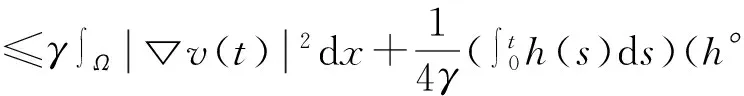
把上式代入(11)式，得

ψ″(t)+ψ′(t)

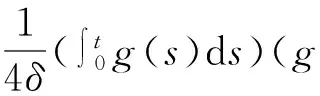
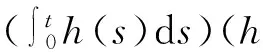
(12)

根据(4)式可知

因此，

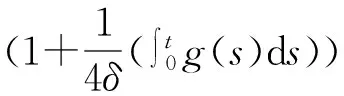
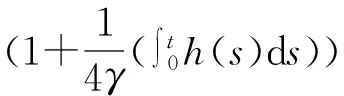
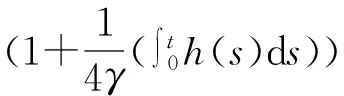
再由引理1，可得

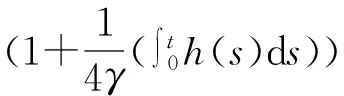
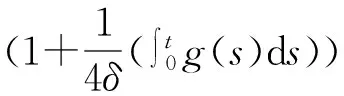
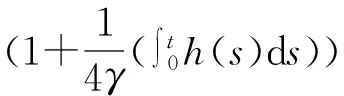
由定理4 的已知条件知存在适当的δ和γ使得

所以存在η>0，使得

(13)

由Hölder不等式知

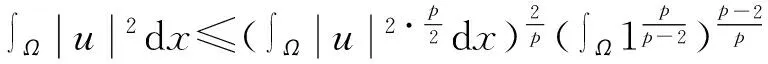
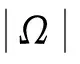
故可得

(14)

(15)

再根据ψ(t)的定义得

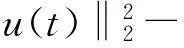
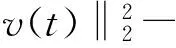
所以对于∀t∈[0,min{T1,T2})，有

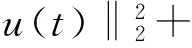
从而可知

(16)

最终，由(13)式-(16)式可得

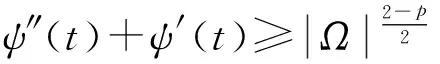
证毕。

[1] MESSAOUDI S A.Blow up and global existence in a nonline-ar viscoelastic wave equation[J].Math Nachr,2003,260:58-66.

[2] MESSAOUDI S A.Blow up of solutions with positive initial energy in a nonlinear viscoelastic equation[J].Math Anal Appl,2006,320:902-915.

[3] WU S T.Blow-up of solutions for an Integro-Differential equat-ion with a nonlinear sourc[J].Electron J Differential Equations,2006,45:1-9.

[4] SONG H T.Blow up of arbitrarily positive initial energy soluti-ons for a viscoelastic wave equation[J].Nonlinear Analysis Real World Applications,2015,26:306-314.

[5] CAVALCANTI M M,CAVALCANTI V D,FERREIRA J.Exis-tence and uniform decay for a nonlinear viscoelastic equation with strong damping[J].Math Methods Appl Sci,2001,24(14):1043-1053.

[6] MESSAOUDI S A,TATAR N E.Global existence and asympt-otic behavior for a nonlinear viscoelastic problem[J].Math Sci Res J,2003,7(4):136-149.

[7] MESSAOUDI S A,TATAR N E.Global existence and stability of solutions for a quasilinear viscoelastic problem[J].Math Methods Appl Sci,2007,30(6):665-680.

[8] WU S T.General decay of solutions for a viscoelastic equation with nonlinear damping and source terms[J].Acta Math Sci Ser B,2011,31(4):1436-1448.

[9] XU R Z,YANG Y B,LIU Y C.Global well-posedness for stro-ngly damped viscoelastic wave equation[J].Appl Anal,2013,92(1):138-157.

[10]KAFINI M,MUSTAFA M I.Blow-up result in a cauchy visc-oelastic problem with strong damping and dispersive[J].Non-linear Analysis:Real World Applications,2014,20:14-20.

[11]SAIDHOUARI B,MESSAOUDI S A,GUESMIA A.General decay of solutions of a nonlinear system of viscoelastic wave quations[J].NoDEA,2011,18(6):659-684

[12]CHEN W,ZHOU Y.Global nonexistence for a semilInear Pet-rovskyequation[J].Nonlinea Anal,2009,70:3203-3208.

[13]LI G,SUN Y,LIU W.On asymptotic behavior and blow up of solutions for a nonlinear viscoelastic petrovsky equation with positive initial eaergy[J].J Funct Spaces Appl,2013(4):1-7.

Finite time blow up for a class of coupled viscoelastic wave equations

DONG Li,LIU Yulong

(School of Mathematical Sciences,Shanxi University,Taiyuan,Shanxi 030006,China)

This paper deals with the initial boundary value problem for a class of coupled viscoelastic wave equations with strong damping term and dispersive term .By using convexity method ,a finite time blow-up result under certain conditions on the inital data and the relaxation function is given out.

viscoelastic;coupled wave equation;initial boundary value problem;blow up

1004—5570(2016)05-0049-05

2016-04-26

国家自然科学基金资助项目(61174082);国家自然科学青年基金资助项目(61104129)

董 莉(1990-)，女，硕士研究生，研究方向：偏微分方程,E-mail:617408853@qq.com.

O175.29

A