变压器油中气体监测数据随机误差的自适应检验方法

邬蓉蓉张 炜樊宇璐邓雨荣张玉波

（1.广西电网有限责任公司电力科学研究院，南宁 530023；2.广西电网有限责任公司崇左供电局，广西 崇左 532200）

变压器油中气体监测数据随机误差的自适应检验方法

邬蓉蓉1张 炜1樊宇璐2邓雨荣1张玉波1

（1.广西电网有限责任公司电力科学研究院，南宁 530023；2.广西电网有限责任公司崇左供电局，广西 崇左 532200）

提出并应用了基于格拉布斯准则检验变压器油气监测数据随机误差的自适应处理方法，扭转了缺少自动甄别正态分布下监测数据随机误差手段的被动局面，降低了误告警的概率。首先，对监测数据序列进行分类、排序等预处理，并计算其样本均值、样本标准差；其次，计算序列中最小、最大数据的样本偏离值；再次，基于格拉布斯准则迭代检验各类监测组分的气体，直至排除所有随机误差异常值。实际应用效果表明，该方法改进了监测系统的纠错能力，提升了监测预警的效果。

变压器；油中溶解气体；格拉布斯准则；正态分布；检验；随机误差

变压器油中溶解气体监测技术已在电力行业广泛应用，并实现了在省级监测主站系统平台的集中监视[1-2]。然而，在对监测数据的利用和分析方面还存在局限[3-5]。一方面受限于电子元件老化、外部环境干扰、载气欠压等现场影响因素，导致监测数据产生误差，甚至导致误告警；另一方面，监测主站系统平台在归集大量数据后，缺乏对数据的分析处理手段；因而依然需要依靠人工经验而分析数据和预测故障，亦未能实现对数据有效及时的自动纠错。

针对现场影响因素，现阶段已采取了提升装置抗干扰性能、改进色谱峰识别方法等控制措施，并取得一定的效果[5]。然而且受限于缺少充分分析监测数据重复性的依据，未能甄别此类错误数据可疑值，导致当前的监测主站系统平台无法有效实现误差数据的自动纠错，进而产生误告警或漏告警。究其主要原因，在于测量精度等原因产生系统误差、随机误差的错误数据，并影响监测数据的重复性。

因此，本文在分析监测数据序列间内在联系的基础上，提出、应用基于格拉布斯准则的自适应筛查处理油中溶解气体监测数据方法，以检验、剔除监测数据中的测量误差，避免因随机误差而导致误告警、漏告警，提升监测系统预警结果的准确性。

1 测量精度分析

由于监测结果易受现场环境、变压器及监测装置状态变化等“小概率事件”的影响，其监测数据序列遵循连续随机变量概率分布，属正态分布（Gaussian distribution）的特征[7-9]。因此，要提高油中溶解气体监测水平，避免误告警和漏告警，其关键在于提高测量精度。按DL/Z 249中的技术指标要求，测量精度包括重复性和误差[10]，结合油中溶解气体监测数据的特点具体阐述如下：

1）重复性：即是指判断测量数据的分布是否在平均值处，或者每个测量数据是否接近。变压器在正常运行状态下的监测数据大幅变化概率低，故影响重复性的因素通常是测值增量。

2）测量误差：包括系统误差、随机误差，是指测量值参考真实值的一致性。分析测量误差的途径主要是比对分析已知材料。在实际应用中通常是指比对监测装置与实验室色谱仪对同一油样的测量结果，其误差应符合DL/T 722中不同实验室间相差不应大于平均值的30%的要求；但实验室的检测频次（每季度一次）远低于在线监测的频次（每日一次），比对的时效性难以满足要求。并且误差亦受制于监测装置的最低检出限。比对分析系统误差、随机误差的产生原因、特点及影响结果见表1。

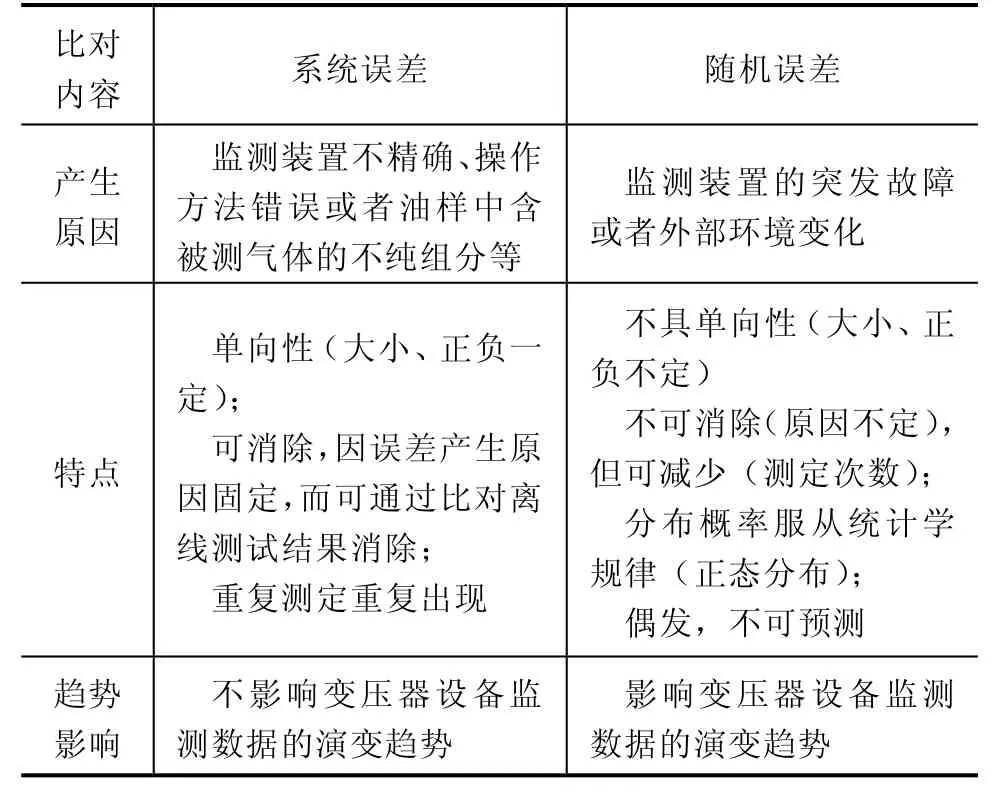
表1 系统误差的随机误差比对分析

视上述重复性、测量误差两类测量精度指标的不同效果，在组合后则可能存在四类情况，如图 1所示。

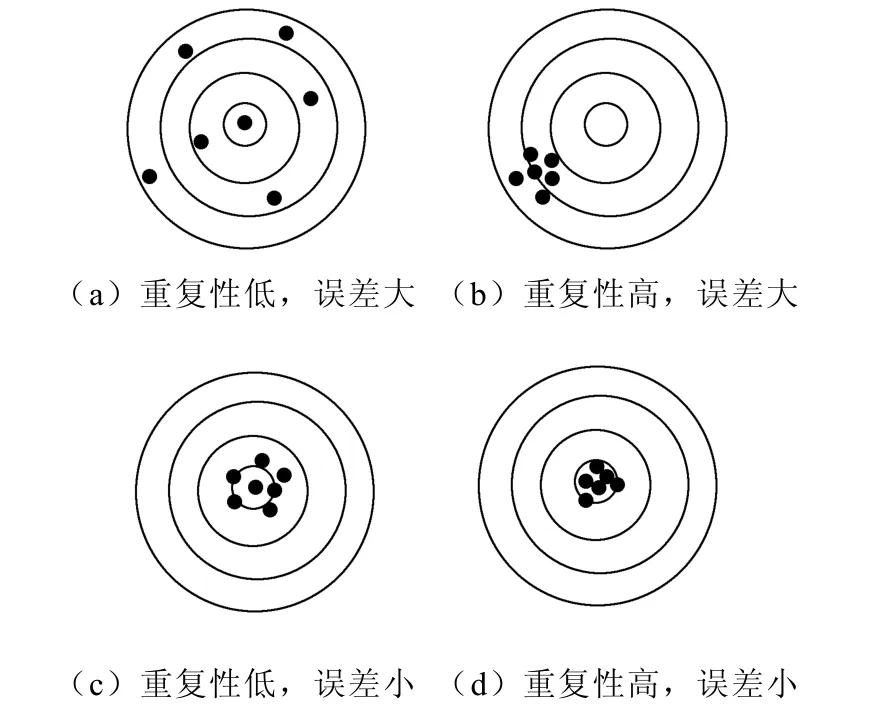
图1 四类不同的测量精度

鉴于上述分析，随机误差有碍于正确判断变压器设备状态影响，而且难以有效筛查、消除误差；故需要通过研究应用筛查、排除因干扰所产生随机误差的方法，并可验证监测数据重复性，以在一定程度上避免监测误告警。统计学中的格拉布斯准则正是以正态分布为前提的校验规则，符合油中溶解气体监测数据产生规律的应用条件，可用于建立检验流程。

2 监测数据可疑值检验方法

2.1 格拉布斯准则

格拉布斯准则是在未知总体标准偏差σ(x)的情况下，对正态样本或接近正态样本异常随机变量进行判别的一种自适应处理方法，已经实验证明是效果较好的判据[11-13]。具体方法如下：

设n个样本值按大小顺序排列x1≤x2≤…≤xn，对其中的最大或最小数据，用格拉布斯准则检验，若残差满足下式：

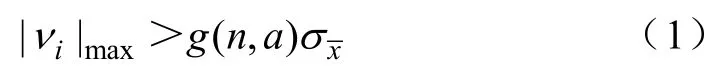
则判断此值为异常数据，应予以剔除。

2.2 检验方法

油中溶解气体监测数据通常包含 H2、CH4、C2H6、C2H4、C2H2、CO、CO2等气体浓度值，因此需基于格拉布斯准则分别检验每一类监测数据的可疑值。首先，计算监测数据的样本均值、样本标准差；其次，分别计算x1和xn的偏离值 ν1、νn；再次，若 ν1＞ νn则以x1进行可疑值检验；反之则以xn进行检验。此外，由于可能出现不止1个可疑值，故还需进行迭代检验。

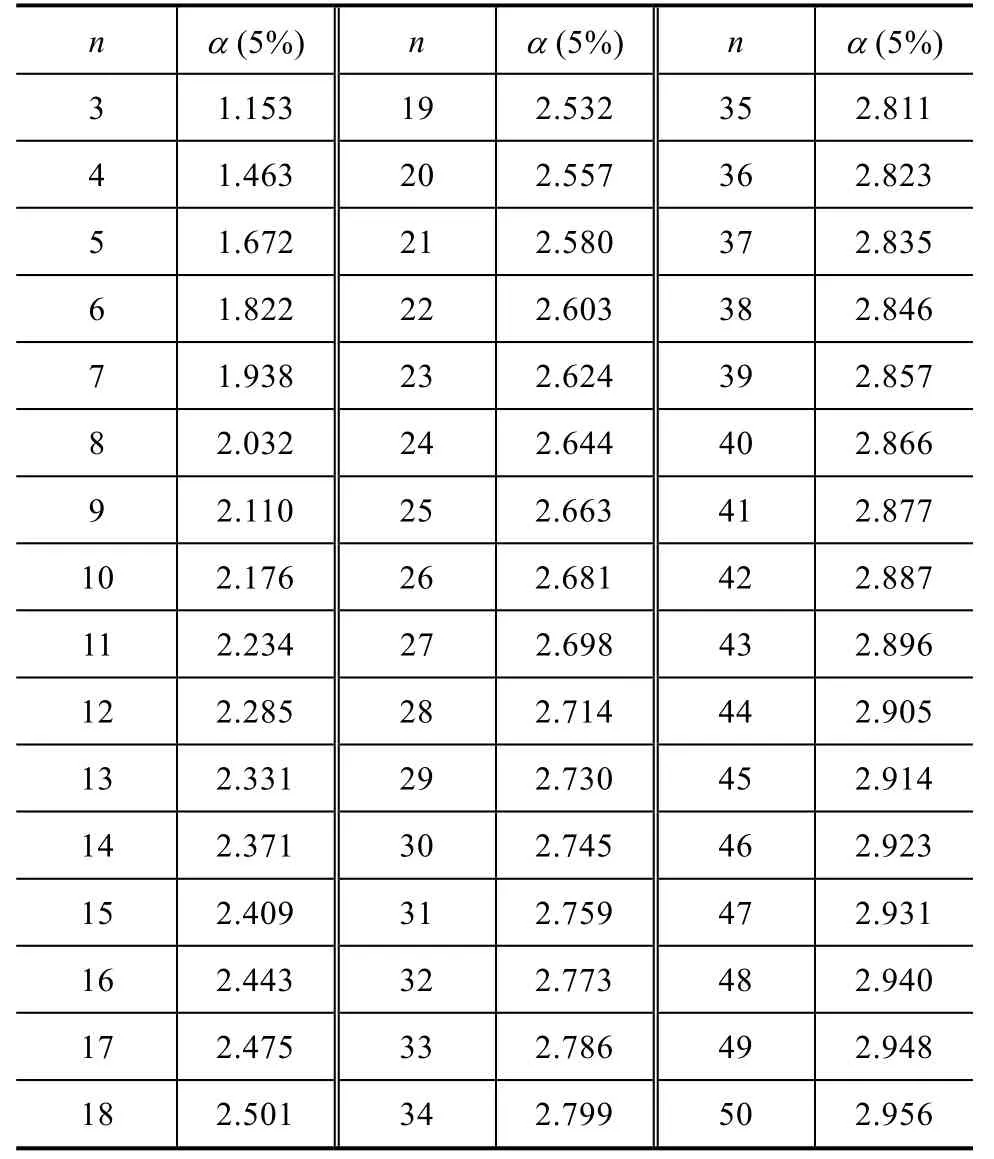
表2 油中溶解气体监测显著性水平α 经验值表

2.3 自适应检验流程

具体方法步骤如图2所示，具体步骤说明如下。

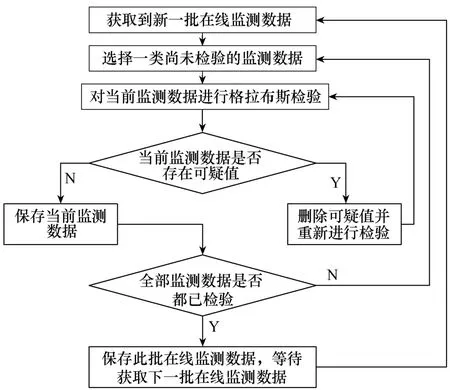
图2 基于格拉布斯准则的检验步骤

1）数据采集：通过在线监测主站系统平台采集分布在各地变压器的监测数据。

2）数据预处理：在主站系统平台内对监测数据进行分析，并提取某一类监测数据待进行格拉布斯迭代检验。即假设监测数据为n个，从小到大排序为：x1≤x2≤…≤xn。

其中样本均值的计算公式如下：

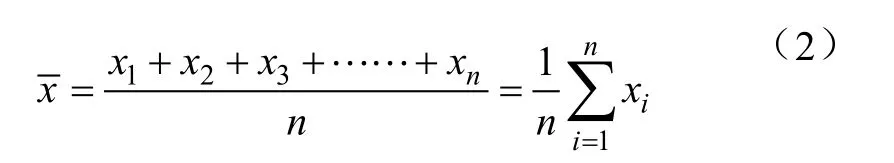
而样本标准差的计算公式为

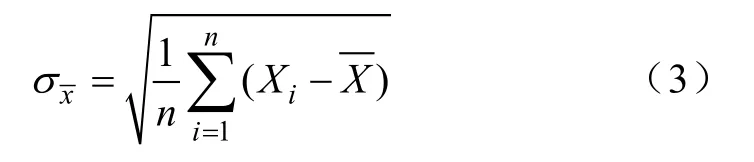
式（2）、式（3）中n为监测数据个数，Xi为监测数据值。

4）计算x1和xn的偏离值ν1、νn。

其中最小值的样本偏离值的计算公式如下：

而最大值的样本偏离值的计算公式为：

若ν1＞νn则以x1进行可疑值检验，反之则以xn进行检验。

5）基于格拉布斯准则的迭代检验。采用式（1），并结合α 经验值表进行检验，若满足则判定该值为可疑值，并予以删除。然后再重新计算样本均值和样本标准差，再重复以上过程。

若不满足式（1），则判定该值可用，本类监测数据检验结束。

6）分类检验。对其他监测测量采用与步骤（3）、（4）相同的方法进行自适应的检验处理，以保证在对随机误差进行筛选、剔除处理之后，各类不同特征数据量具有一致性。则完成监测数据检验；并可进入下一个周期，重复以上过程。

3 算例分析

3.1 算例场景

2016年2月4日，主站系统平台监测发现220kV谊祥站 1号主变的氢气测值达到既定的告警值（150μL/L），但是根据人工经验分析监测数据时，则会发现除氢气突然越升至告警值以上外，乙烯、甲烷、乙炔等烃类组分气体均为零；这显然与当变压器的过热类或放电类故障时会同时产生氢烃组分气体的表像不符[14-15]，故此数据应为随机误差。然而，传统的监测程序并不具备此类人工智能筛查分析的能力，仍然会误告警设备异常，干扰正常的设备预警与运维。

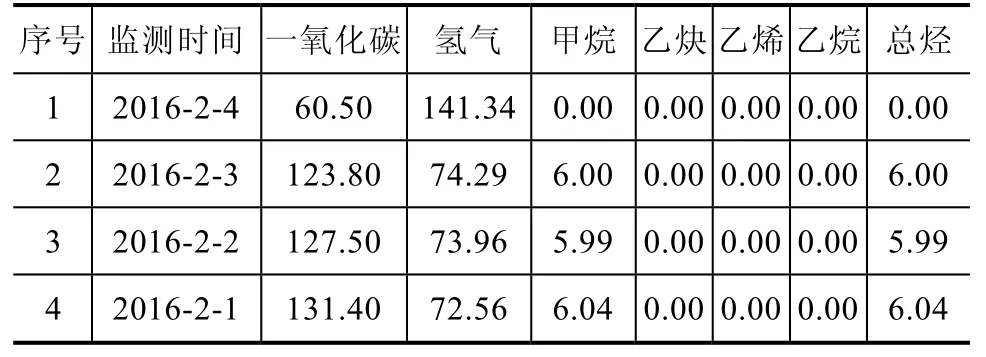
表3 系统告警时的监测数据

当在主站系统平台中配置基于格拉布斯的监测程序后将检验出现显著变化的一氧化碳（CO）和氢气（H2），并对随机误差进行纠错。

1号主变近一个月的一氧化碳（CO）和氢气（H2）监测历史数据见表3，监测数据曲线如图3所示。

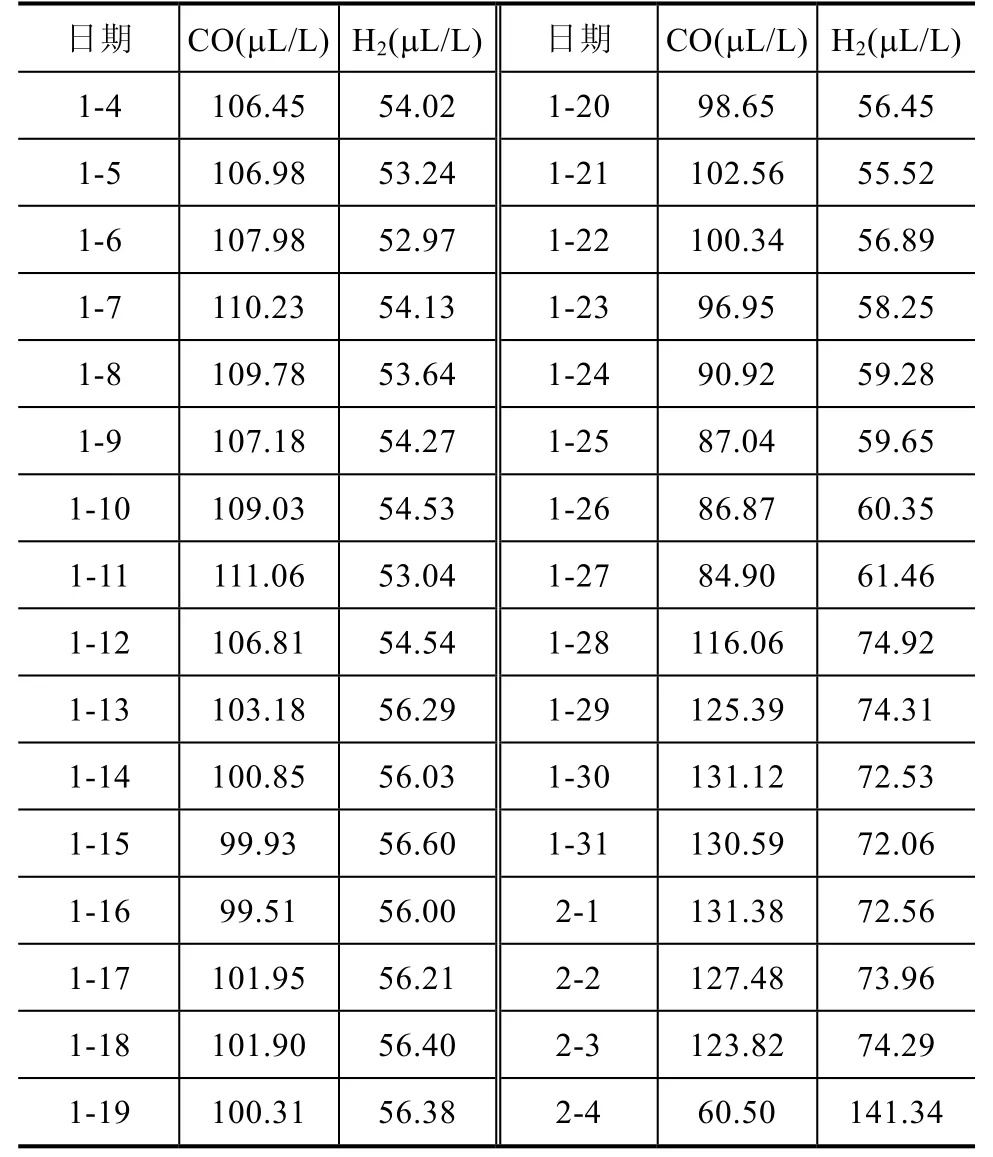
表4 CO和H2的监测历史数据

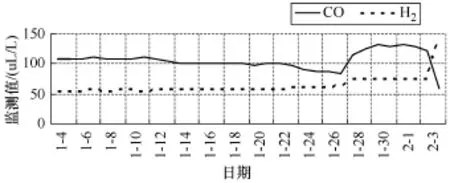
图3 监测数据历史曲线

3.2 演算过程

针对2016年1月4日到2016年2月4日的监测数据样本，分别对CO和H2进行可疑值检验分析，具体过程如下：

1）检验分析CO的监测数据

（2）计算样本最大最小值的偏离值：ν1=45.05；νn=25.83。因为ν1＞νn，所以选择样本最小值（60.5）进行可疑值检验。

（3）取a=0.05，查a经验值表，得g( n,a)=2.773。计算g( n,a)=41.76，小于 ν1（45.05），则判断样本最小值（60.5）为异常值，即2月4日的CO监测值为异常值，应予以剔除。

2）检验分析H2的监测数据

（2）计算样本最大最小值的偏离值：ν1=9.6；νn=78.77。因为ν1＜νn，所以选择样本最大值（141.34）进行可疑值检验。

（3）取a=0.05，查a经验值表，得g( n,a)=2.773。计算g( n,a)小于 νn（78.77），则判断样本最大值（141.34）为异常值，即2月4日的H2监测值为异常值，应予以剔除。

至此，结束对220kV谊祥站1号主变油气监测数据的自动检验分析过程，初判2月4日监测数据数据随机误差；并提示设备运维人员检查分析。经事后检查，确认监测装置存在加温故障，验证此方法可有效自动筛查出异常变化的数据，并利于及时复核异常变化的原因。

4 结论

本文在分析监测数据的显著性差异特征的基础上，提出并应用了基于格拉布斯准则而迭代检验、甄别监测数据的方法，达到自适应筛查因异常干扰等产生的随机误差的目的，并且降低了监测误告警和漏告警的概率。同时，由于在主站系统平台具备自动分析和处理错误数据的能力，也将进一步提升系统处理大规模监测数据的能力，并降低人工分析排查监测误告警的工作量。

[1]刘娟,鞠登峰,王勇,等.变电站设备智能状交览测系统的设计及应用[J].电力建设,2012,33(6):6-10.

[2]王峰,阎春雨,毕建刚,等.变电设备状态监测系统的设计方案[J].电力建设,2011,32(11):31-35.

[3]肖燕彩,朱衡君,张霄元,等.基于溶解气体分析的电力变压器在线监测与诊断技术[J].电力自动化设备,2006,26(6):93-96.

[4]张炜,梁俊斌,邓雨荣,等.变压器绝缘油中产气趋势突变的检测方法研究[J].绝缘材料,2015,48(10):72-76.

[5]李洪超,王伟刚,董雪梅.基于M-LS-SVR的变压器油中溶解气体浓度预测[J].电气技术,2016,17(1):76-80.

[6]赵婉芳,王慧芳,邱剑,等.基于油色谱监测数据的变压器动态可靠性分析[J].电力系统自动化,2014,38(22):38-42,49.

[7]曹建,范竞敏,安晨光,等.灰色关联度分析在变压器油色谱峰辨识中的应用[J].电网技术,2010,34(7):206-210.

[8]尹金良,朱永利,俞国勤,等.基于高斯过程分类器的变压器故障诊断[J].电工技术学报,2013,28(1):158-164.

[9]张艳珠,李媛,李小娟.简化型 PCNN的混合噪声图像滤波算法研究[J].控制工程,2013,20(5):829-832.

[10]DL/Z 249.变压器油中溶解气体在线监测装置选用导则[S].国家能源局,2012.

[11]陈锐,周书民.改进的格拉布斯准则在氡浓度计数中的应用[J].核电子学与探测技术,2009,29(1):113-115.

[12]唐慧强,刘钲江,李全月.硫氮分析系统异常值自动甄别与纠错方法研究[J].传感器与微系统,2013,32(9):42-45,49.

[13]李梦奇,白晓军,匡同春,等.工程技术领域等精度数据异常值判定系统[J].计量技术,2006(3):57-59.

[14]杨超.一起在线监测发现 500kV变压器缺陷的分析及处理[J].电气技术,2014,15(9):74-77.

[15]徐康健.变压器油色谱分析中用三比值法判断故障时应注意的问题[J].变压器,2010,47(1):75-76.

Adaptive Test Method for Random Error of Dissolved Gas Monitoring Data in Transformer Oil

Wu Rongrong1Zhang Wei1Fan Yulu2Deng Yurong1Zhang Yubo1
(1.Electric Power Science Research Institute of Guangxi Power Grid Co.,Ltd,Nanning 530023;2.Chongzuo Power Supply Bureau of Guangxi Power Grid Co.,Ltd,Chongzuo,Guangxi 532200)

Study on the adaptive test method for random error of dissolved gas monitoring data in transformer oil,to change the passive situation of the lack of automatic diagnosis of random error means，reduces the probability of false alarm and missing alarm.First,the data classification,sorting,and calculate the average value of the data,the standard deviation.Secondly,the deviation value of the minimum data and the maximum data in the data sequence is solved.Finally,the iterative test monitoring data based on Grubbs criterion,until the exclusion of all outliers.The actual application results show that this method improves the error correction capability of the system,but also enhance the effectiveness of monitoring and early warning.

transformer;dissolved gases;Grubbs criterion;Gaussian distribution;test;random error

邬蓉蓉（1984-），女，硕士，工程师，主要从事电力设备状态监测与故障诊断研究工作。

南方电网公司科技项目（GX2014-2-0025，K-GX2014-020）