电流型IPT系统新型输出恒压控制方法研究

阚超豪 朱晓威 程 源

（合肥工业大学电气与自动化工程学院，合肥 230009）

电流型IPT系统新型输出恒压控制方法研究

阚超豪 朱晓威 程 源

（合肥工业大学电气与自动化工程学院，合肥 230009）

针对电流型感应电能传输（IPT）系统负载变化时输出电压的稳定性问题，提出一种基于恒定跨阻增益特性的原边控制方法。以电流型IPT系统采用初次级并联（PP）补偿为研究对象，建立其互感等效电路并进行分析，推导出在特定工作条件下该拓扑具有恒定跨阻增益特性。并进一步分析了PP补偿谐振网络的效率特性，优化谐振网络参数使系统恒定跨阻增益频率为效率最优频率。为保持原边输入直流母线电流恒定，在传统电流型感应电能传输拓扑中加入恒流控制系统，并阐述了恒流控制原理。本文还提出了基于新型控制方法在给定条件下的IPT系统综合设计方法。最后，设计一台80W样机，实验结果与理论分析良好吻合，验证了论文所提控制方法的正确性。

电流型感应电能传输；恒定跨阻增益；效率优化；恒流；非接触变压器

IPT系统是基于电磁感应原理实现“无线供电”的新型电能传输模式，与传统供电模式相比，具有安全、灵活、环境适应能力强等优点。在电动汽车、小家电以及易燃易爆、水下等特殊环境的用电设备等方面有广阔的应用前景[1-5]。

IPT系统负载变化容易导致系统输出性能下降，因此需要采用合适的控制方法保证输出性能的稳定。对于电流型IPT系统文献[6]提出在副边增加相控电抗器，通过控制相控电抗器的导通延迟角来改变导通电流大小，使负载端获得稳定的输出电压。文献[7]的控制方法是采用副边加入Boost环节调压来实现原、副边解耦。以上控制方法虽然都能够实现在一定负载范围内输出稳压，但增加了系统的控制成本和副边电路结构的复杂性。

在此提出基于电流型IPT系统恒定跨阻增益特性的原边控制方法。恒定跨阻增益特性是指系统工作在恒定跨阻增益频率下，只要保证系统原边输入直流母线电流恒定，副边输出电压即恒定的特性。该控制方法具有控制成本低和副边电路结构简单的优点。以PP补偿为例分析了其恒定跨阻增益特性和谐振网络效率特性，优化谐振网络参数使系统的恒定跨阻增益频率为效率最优频率。同时，在系统输入电源端加入Buck变换器，通过控制其占空比保持输入直流母线电流等于设置的恒流控制目标。本文从恒流控制目标出发，提出了基于新型控制方法在给定变压器材料和尺寸、气隙、输入输出电压、效率最优、最大输出功率条件下包括谐振网络参数、恒流控制目标和非接触变压器设计在内的IPT系统综合设计方法。

1 系统原理与恒定跨阻增益特性分析

1.1 电流型PP补偿IPT系统结构

电流型 PP补偿 IPT系统包括原边与副边两部分，系统结构如图1所示，原边主要包括由直流电压源Uin和输入滤波电感Ldc组成的等效电流源、高频逆变功率管V1—V4、串联缓冲电感L1—L4、环流阻断二极管VD1—VD4、原边补偿电容Cp及原边发射线圈电感Lp。副边主要包括副边接收线圈电感Ls副边补偿电容Cs及负载R。M为原、副边线圈互感，k为原、副边线圈耦合系数，可表示为：

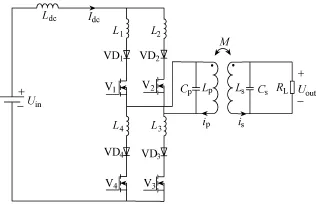
图1 PP补偿IPT系统结构

1.2 恒定跨阻增益特性分析

根据互感模型法对主电路进行分析，电流型IPT系统采用PP补偿的分离互感等效电路如图2所示。图 2中：Rp、Rs为原、副边线圈等效串联电阻，Zr为副边折射会原边的反射阻抗。

式中，Zs为副边等效阻抗，Zs=jωLs+Rs+R/(1+jωCsR)。原边输入总阻抗Zin为

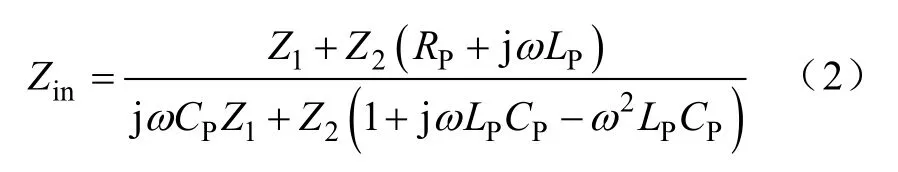
式中，Z1=ω2M2+jω3CsR；Z2=R+jωLs−ω2LsCsR+ Rs(1+jωLsR)。

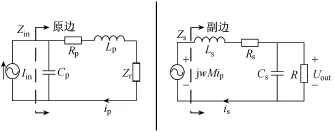
图2 PP补偿分离互感等效电路

由图2可得，副边输出电压可表示为

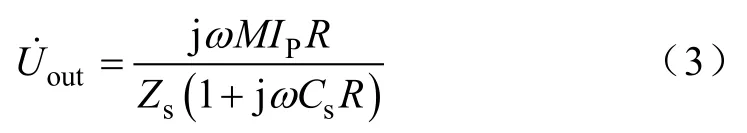
原边输入电流Idc的基波分量为

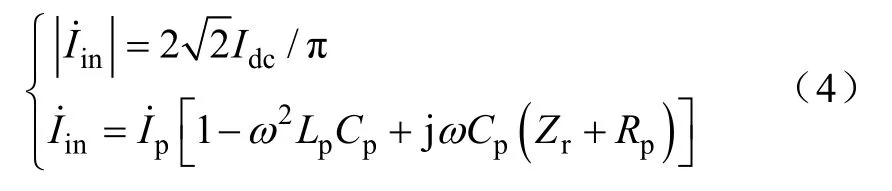
由于Rp、Rs与负载电阻R相比很小，对跨阻增益影响很小，为了便于分析，忽略其影响。由式（3）、式（4）可得跨阻增益为

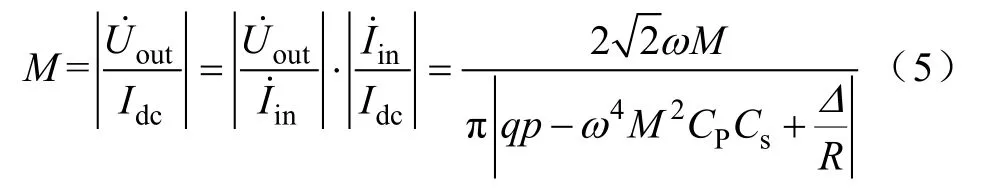
式中，Δ=jωLs(1−ω2LpCp)+jω3M2Cp，p=1−ω2LpCp，q=1−ω2LsCs。

当Δ=0时，系统的跨阻增益与负载无关，对应的恒定跨阻增益角频率ωN为

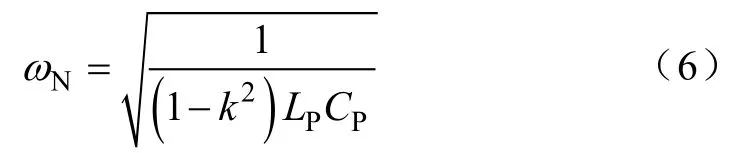
相应的跨阻增益为

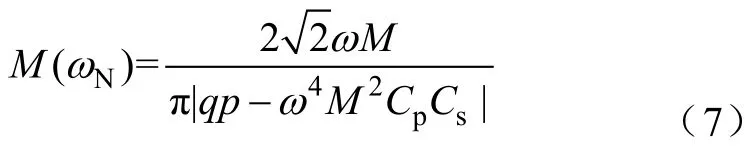
由式（6）可知，恒定跨阻增益频率略高于谐振网络固有谐振频率，谐振网络呈弱容性，满足逆变功率管的软开关条件。

2 谐振网络效率优化分析

PP补偿IPT系统的有功损耗主要集中在谐振网络中，本部分通过分析PP谐振网络的效率特性，结合其恒定跨阻增益特性，优化谐振网络参数使系统恒定跨阻增益频率为效率最优频率。由于谐振电感线圈的等效串联电阻比谐振补偿电容的等效串联电阻大的多，所以在分析效率时只考虑电感线圈的等效串联电阻的损耗。谐振网络的总效率η 可表示为

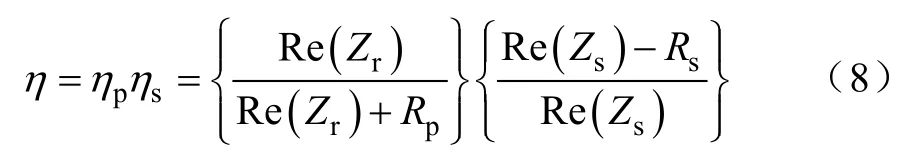
式中，ηp为原边效率；ηs为副边效率。

对于PP补偿网络，效率表达式为

式中，Qp为原边线圈品质因数，QP=ωLp/Rp；Qs为副边线圈品质因数，Qs=ωLs/Rs；QL为负载品质因数，

令dη/dω=0可得

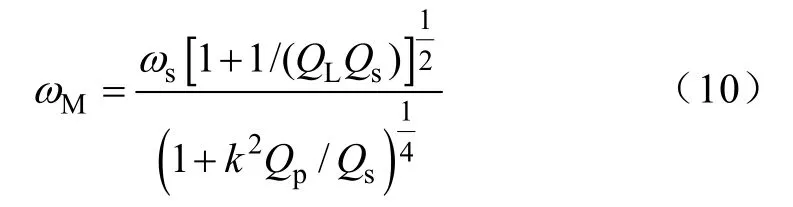
经验证效率在ωM处取得最大值。一般原、副边线圈选择相同的导线，QP=Qs，且QLQs>>1，所以ωM的值与负载无关。使ωM=ωN，此时谐振网络参数满足：

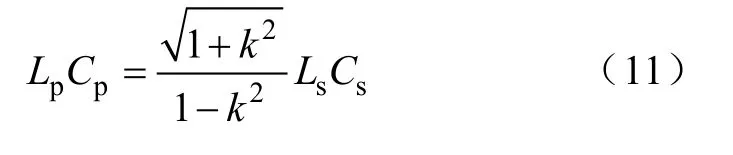
相应的跨阻增益为

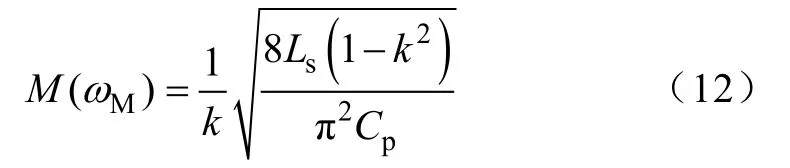
3 恒流控制系统设计

为了保持输入直流母线电流恒定，在输入电源端加入Buck型变换器，系统框图如图3所示，Va、Vb为Buck环节功率管，两管互补导通，电感Li和电容 Ci支路的作用是在工作过程中使 Va、Vb管中电流反向，为两管的软开关提供条件，具体软开关过程请参考文献[8]，本文不再赘述。为了保证Buck环节与逆变环节同步工作，Buck环节工作频率应为逆变环节的两倍[9]。控制系统通过采样电感电流峰值，前馈与恒流控制目标 It比较，控制功率管驱动脉冲占空比，从而使电感电流峰值保持恒定。选择合适大小的输入滤波电感使输入电流纹波达到要求，此时电感电流峰值近似等于电感电流平均值，达到控制输入直流母线电流恒定的目的。

3.1 恒流控制目标和非接触变压器设计

恒流控制目标和非接触变压器的设计是恒定跨阻增益控制方法的关键，谐振网络参数、输出功率、效率等都与两者有关。由式（3）可得输入相角ϕ为

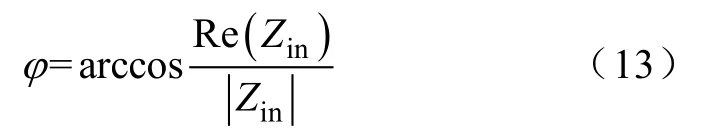
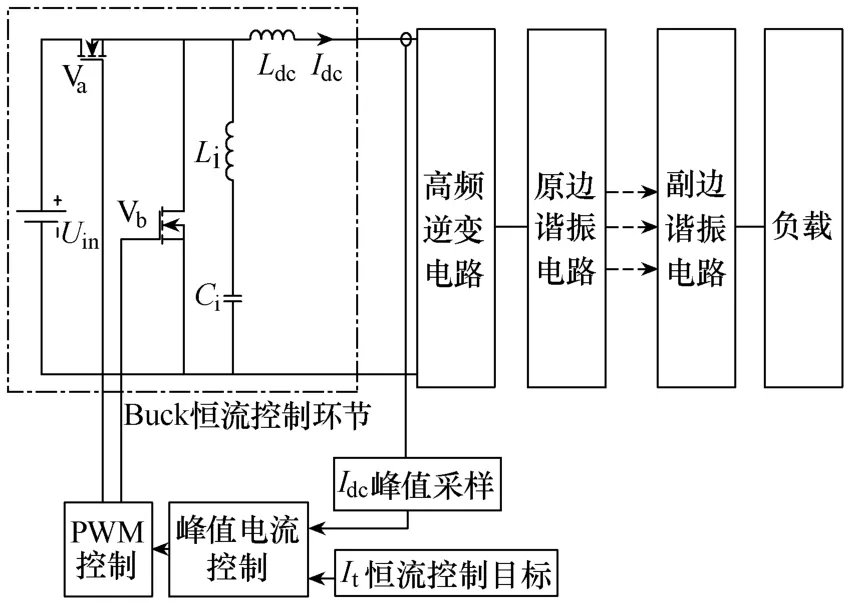
图3 恒流控制系统框图

Buck环节和逆变器环节的有功损耗主要包括功率管和二极管的导通损耗、输入滤波电感和串联小电感等效电阻损耗。设以上损耗的等效损耗电阻为Req，系统最大输出功率为Pout，恒流控制目标为It，则原边输入视在功率Sin为

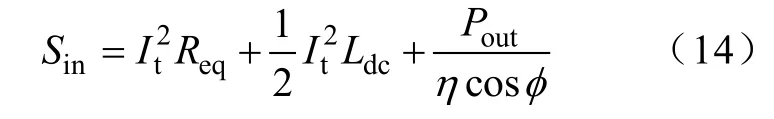
根据文献[5]中 Buck环节功率管软开关的实现条件，可得Va管驱动脉冲最大占空比为D，则实际需要输入的电流Idc为

非接触变压器采用文献[10]提出的带有平面磁心和铝屏蔽层结构，此结构具有耦合系数大、漏磁通小等优点，结构如图4所示。文献[11]给出了线圈螺旋绕制且绕组半径不超过磁平面半径一半时的自感、互感的计算方法。

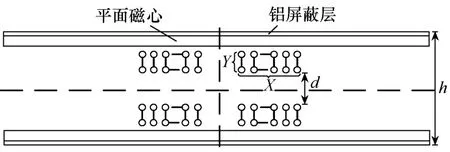
图4 非接触变压器结构

非接触变压器参数和恒流控制目标与输出功率、效率等设计指标相互关联，需要通过迭代才能设计出满足变压器材料和尺寸、气隙、输入输出电压、效率最优、最大输出功率条件的非接触变压器和恒流控制目标。已知耦合系数为 k，输出电压为Uout，迭代过程如图5所示，设计步骤如下：

1）初选恒流控制目标It，将It、Uout、k带入式（12）可得满足输出电压要求的Ls/Cp值。

2）为了简化设计，令Cp=Cs，为达到效率最优，由式（11）可得Lp/Ls的值。

3）初选补偿电容值Cp、Cs，可得Lp、Ls的值，如果此时的恒定跨阻增益频率超过磁心的频率范围，则增大Cp、Cs的值重新计算。设每层绕制匝数为X，共Y层，可得匝数N=XY。初选X=1、Y=1，根据文献[7]中的公式Lpeq、Lseq计算，如果Lpeq、Lseq小于Lp、Ls，则在Y不变的情况下增大X，重新根据公式迭代计算，当线圈半径超过磁面半径一半时，保持X不变增大Y。

4）在步骤3）中增大Y会增大变压器尺寸，当变压器尺寸超过规定尺寸时，需要减小Cp、Cs，返回步骤 3）重新迭代计算，减小变压器尺寸，使其满足要求。

5）根据设计出非接触变压器计算Rp、Rs，结合Cp、Cs、Lp、Ls、Req带入式（9）、式（13）求出效率和输入相角，进而结合It、D、Uin由式（14）、式（15）计算得到实际输入电流 Idc。如果 It＜Idc，则增大恒流控制目标返回步骤 1）重新计算，即增大输出功率，使其满足输出功率要求。

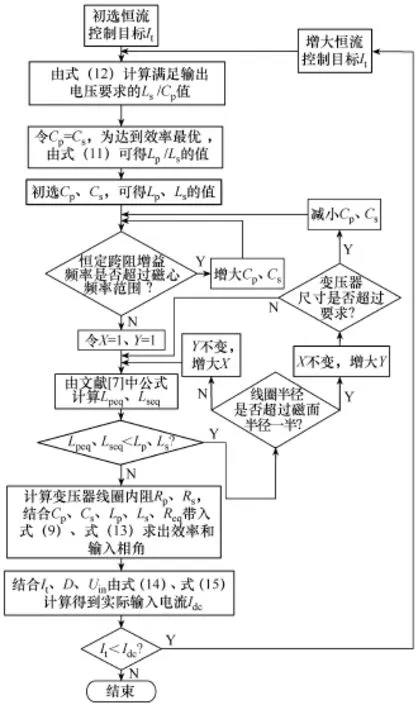
图5 IPT系统设计流程

由于没有考虑电路寄生参数的影响，所以实际设置的恒流控制目标略高于设计值，相应的调整补偿电容大小来满足输出电压要求，非接触变压器的设计不需要改变。

4 实验

为了验证上述分析，按图3搭建了一台80W原理样机，主要样机参数：直流侧输入电压Uin=24V；Buck环节最大占空比 D=0.94；输入滤波电感Ldc=1mH；原、副边补偿电容Cp=Cs=2.5μF；恒定跨阻增益频率fN=25kHz；输出电压峰值Uout=40V；控制系统以LM5041级联PWM控制器为核心。根据文章第4部分的分析，设置恒流控制目标It=4A，非接触变压器磁心选用TDK公司的铁氧体材料PC40，磁心尺寸为 100mm×100mm×10mm，气隙长度 d=10mm。线圈选用 0.1mm×300股丝包线绕制，原边共三层，每层 10匝，副边共三层，前两层每层 10匝，第三层6匝，QP=Qs=200。按照文献[11]的计算方法得到的非接触变压器参数计算值与实测值对比见表1，可见两者基本吻合。

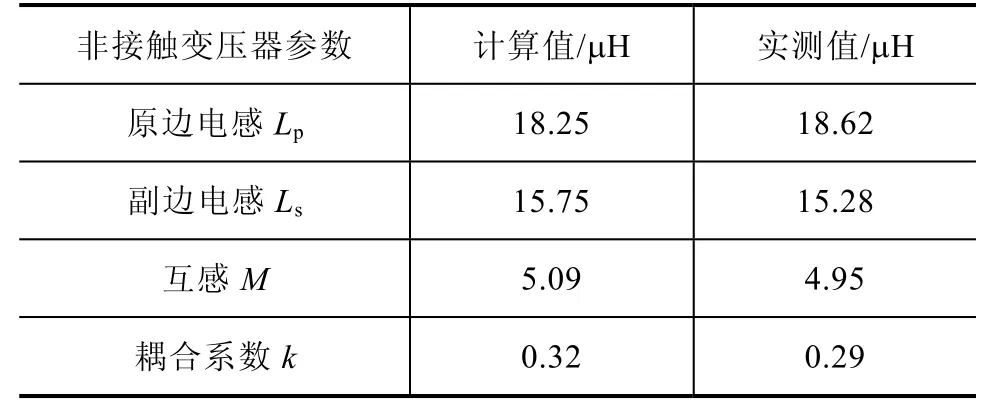
表1 非接触变压器参数计算值与实测值

图6（a）、（b）分别给出负载为 50Ω和 10Ω时的功率管Va驱动脉冲ugva、输入直流母线电流Idc、输出电压Uout波形。可见，Buck环节工作频率是逆变环节的两倍，Idc、Uout在负载变化时保持不变。由于Buck环节和原边逆变电路切换造成Idc0.2A左右的纹波扰动，达到设计要求。

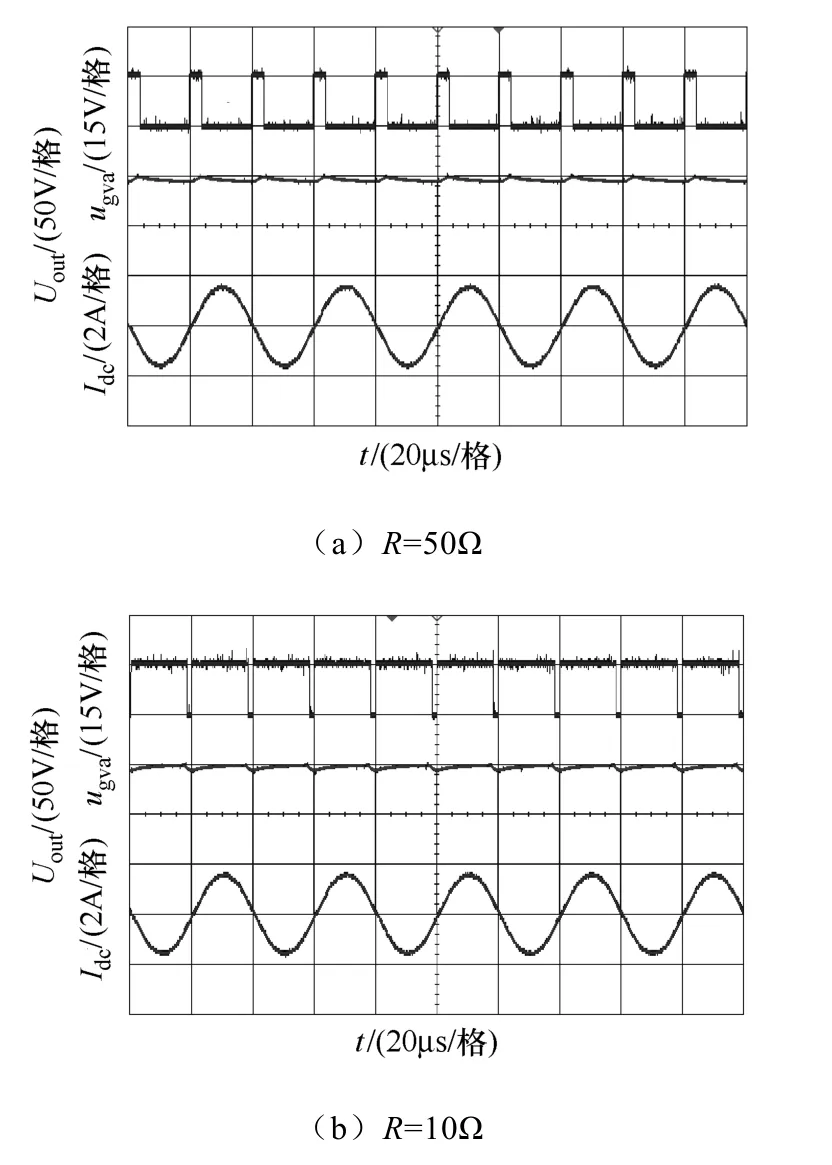
图6 不同R下的稳态实验波形

图7给出了负载从10Ω跳变到50Ω时，Idc、Uout的动态波形。由图可见，在控制作用下Idc经历了1个1.2A左右的超调，Uout经历了1个11V左右的超调，经过 500μs左右的调节过程后进入稳态，图 7与图6稳态波形一致。实验结果说明恒流控制系统对于负载变化具有较好的抑制作用，也验证了上文分析与设计的有效性和正确性。

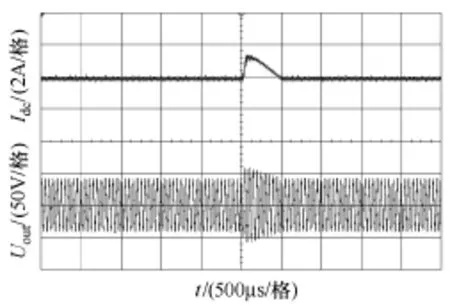
图7 负载跳变动态实验波形

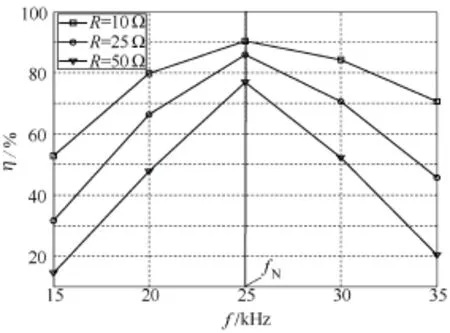
图8 效率随工作频率的变化曲线

图8为不同负载电阻条件下系统的效率随工作频率变化曲线。可见，恒定跨阻增益频率为效率最优频率，最高效率达到90.6%。

5 结论

本文对基于恒定跨阻增益特性的电流型IPT系统输出恒压控制策略进行研究，理论分析和实验验证表明：当系统工作在恒定跨阻增益频率时，输出电压仅于输入直流母线电流有关，与负载无关，且恒定跨阻增益频率为系统效率最优频率，最高效率达到 90.6%。恒流控制系统具有很快的动态响应速度和良好的稳态精度。实验结果验证了本文提出的基于新型控制方法的电流型IPT系统综合设计方法的有效性。

[1]Ahn D,Hong S.A study on magnetic field repeater in wireless power transfer[J].IEEE Trans.on Industrial Electronics,2013,60(1):360-371.

[2]Jang Y,Jovanovic MM.A contactless electrical energy transmission system for protable-telephone battery chargers[J].IEEE Trans.on Industrial Electronics,2003,50(3):520-527.

[3]Chen C,Wong SC,Tse CK,et al.Analysis,design andcontrol of a transcutaneous power regular for artificial heart[J].IEEE Trans.on Biomedical Circuit and Systems,2009,3(1):23-31.

[4]杨庆新.无线电能传输技术及其应用[M].北京:机械工业出版社,2014:160-179.

[5]曹玲玲,陈乾宏,任小永,等.电动汽车高效率无线充电技术的研究进展[J].电工技术学报,2012,27(8):1-13.

[6]杨民生,王耀南.感应耦合电能传输系统动态解谐传输功率控制[J].电机与控制学报,2012,16(1):72-78.

[7]Madawala UK,Thrimawithana DJ.New techique for inductive power transfer using a single controller[J].IET Power Electronics,2012,5(2):248-256.

[8]陈世杰,顾亦磊,吕征宇,等.适用于 Buck电路的一种改进型软开关实现方法[J].电力电子技术,2004,38(4):8-10.

[9]黄剑峰,马皓.Buck与推挽级联式DC/DC变换器的研究[J].电力电子技术,2008,42(6):30-32.

[10]韩洪豆,曲小惠.基于恒流源补偿网络的电磁感应式非接触电能传输的LED驱动电路[J].中国电机工程学报,2015,35(20):86-92.

[11]Su Yp,Liu Xun,Hui S.y.ron.Mutual inductance calculation of movable planar coils on parallel surfaces[J].IEEE Transactions on Power Electronics,2009,24(3/4):1115-1123.

Research on Novel Constant-voltage Output Control Method for Current-fed IPT System

Kan Chaohao Zhu Xiaowei Cheng Yuan
(School of Electrical &Automatic Engineering,Hefei University of Technology,Hefei 230009)

The current-fed inductively power transfer (IPT) system,aiming at the Output-Voltage-instability problem on a dynamic load,based on the constant transimpedance gain characteristics of the primary side control method is proposed.Taking current-fed IPT system with parallel-primary and parallel-secondary (PP) compensate as an object,by building and analyzing the mutual inductance equivalent circuit,had the characteristics of constant-transimpedance-gain under certain working conditions are derivated.And the efficiency characteristics of PP compensated resonant network are analyzed,optimization of resonant network parameters make the system constanttransimpedance-gain frequency for the efficiency of the optimal frequency.In order to maintain the constant input bus current,the constant-current control system is added in the traditional current-fed IPT topology,and the principle of constant-current control is described.This paper gave design steps based on the novel control method under given conditions.Finally,designed a 80W prototype,the experimental results are in good agreement with the theoretical analysis and the correctness of the circuit topology and control strategy is verified.

current-fed IPT system;constant transimpedance gain;efficiency optimization;constant current;contactless transformer

阚超豪（1974-），男，安徽省宿州人，博士，副教授，硕士生导师，研究方向为感应电能传输、特种电机及其控制。

国家自然科学基金资助项目（51377040）