基于二次规划的电动汽车入网充放电策略

武小花, 阴晓峰，陈泽宇,张 龙

(1. 西华大学汽车与交通学院，四川 成都 610039；2. 东北大学机械工程与自动化学院，辽宁 沈阳 110819)



·新能源汽车与低碳运输·

基于二次规划的电动汽车入网充放电策略

武小花1, 阴晓峰1，陈泽宇2,张 龙1

(1. 西华大学汽车与交通学院，四川 成都 610039；2. 东北大学机械工程与自动化学院，辽宁 沈阳 110819)

以电动汽车接入家庭用电网(V2H，vehicle to home)系统为研究对象，分析V2H系统结构和主要工作模式；根据V2H系统结构和工作模式，建立V2H系统电池组模型、V2H功率流模型和用电成本模型；基于分时电价和分时家庭用电功率需求，以日用电总成本最小为优化目标，得出基于二次规划的V2H系统电池组充放电控制策略；通过Matlab仿真，以模式C(电池组入网充放电且可放电反馈回电网)为例，用二次规划模型分析电池组荷电状态、充放电电流、V2H系统功率流以及用电成本随时间的变化规律；比较分析基于二次规划控制的V2H工作模式相对于电动汽车即插即充工作模式所能节省的用电成本。结果表明，基于二次规划优化控制的V2H系统可以有效地降低用电成本。

电动汽车入家庭用电网; 充放电优化; 二次规划; 电动汽车

电动汽车的大量发展为电力系统的安全和经济运行带来了新的挑战和机遇，如果大规模电动汽车在电网的负荷高峰时段充电,那么将增大电网负担，影响电网的稳定运行[1-2]。电动汽车有序充放电控制不仅能够限制充电负荷的不利影响，而且能够实现最小化用电成本，负荷削峰填谷，促进可再生能源的吸纳，发挥负荷调度的作用[3-8]。

大量的研究文献表明电动汽车充放电负荷具有一定的可控性。文献[9]研究了大规模电动汽车有序充电优化，得出有序充电可有效减少电网峰荷，平滑负荷，减少或延缓发电、输电和配电设备的投资。在文献[10]中，作者建立了基于动态规划的有序充电模型，评估了多情景下电动汽车充电对配电网的影响。文献[11]表明，在V2H(Vehicle to Home)系统中，通过光伏发电装置和电动汽车电池的有效配合使用，可减少反向潮流和CO2排放。文献[12]运用模糊逻辑控制和随机优化，制定了基于光伏太阳能发电的V2H系统实时控制策略，降低家庭用电成本。文献[13]研究使用不同控制方法时，插电式混合动力汽车充电对电网的影响。本文从规划的角度，基于分时电价和分时家庭电量需求，研究电动汽车接入家庭用电网V2H系统的充放电优化控制对家庭用电成本的影响。

1 V2H系统结构分析

V2H系统结构如图1所示，V2H将家庭电量需求、电网和车载电池组智能地联系在一起，通过控制器实现车载电池组充放电的优化控制，在满足家庭用电需求以及电池组充电要求的条件下，实现最小化用电成本的目标。

图1 V2H系统结构

V2H工作模式主要可以分为4种类型，如图2所示。模式A中电池组仅充电；模式B电池组充放电且可为家庭用电提供电量；模式C在模式B的基础上除为家庭用电提供电量，同时可以放电反馈到电网；模式D在模式C的基础上，同时考虑可再生能源，如风电、光伏太阳能发电等。本文以工作模式A、B和C为基础，通过二次规划制订电动汽车电池组联入家庭用电网后的充放电控制策略。

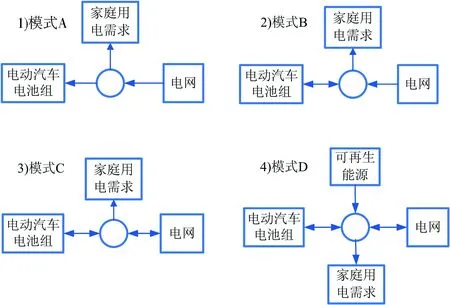
图2 V2H系统模式分类

2 系统模型分析

V2H系统模型主要包括电池模型、车辆联入家庭用电网的功率流模型和用电成本模型。

2.1 电池组模型

当前主流的电池组模型主要包括等效电路模型和电化学模型，电化学模型结构复杂，通常采用等效电路模型进行优化控制[14-15]。本文采用等效电路模型研究电池组充放电对于家庭用电成本的优化控制策略，如下式所示：

(1)

式中: 时间步长k= 0,1,…,N；Pbatt,k为电池组充放电功率；Voc为电池组端电压；Ik为电池组充放电电流；Rint为电池组内阻。

荷电状态SOC(state of charge)是电池组重要的特征参数，其与电流Ik的关系表示为

(2)

式中：Qcap为电池组容量；Δt为采样时间间隔。

2.2 V2H功率流模型

V2H功率流模型存在电动汽车入网和电动汽车出网2种情况。当车辆联入家庭用电网时，V2H系统中电量在电池组、家庭用电设备和电网之间传递，其功率流模型表示为

Pgrid,k=Pdem,k+Pbatt,k。

(3)

式中：Pgrid,k为电网向V2H系统提供的电功率；Pdem,k为家庭用电设备的需求电功率。

当车辆外出行驶时V2H系统中的电量仅在家庭用电设备与电网之间传递，电池组为车辆行驶提供能量，与家庭用电网间没有能量传递，功率流模型表示为

(4)

式中Pv,k为车辆行驶需求功率。纯电动汽车在行驶过程中满足车辆行驶动力学方程，且完全由电池组提供所需能量，车辆行驶功率需求表示为

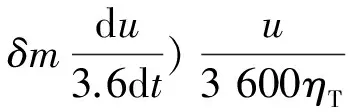
(5)

式中：m为车辆质量；f为滚动阻力系数；g为重力加速度；α为道路坡度；CD为空气阻力系数；A为迎风面积；u为行驶车速；δ为汽车旋转质量换算系数；ηT为机械传动效率。

2.3 用电成本模型

根据电价、家庭用电需求功率、电池组充放电功率、车辆状态即可得到用电总成本为

(6)

(7)

式中：ck为分时电价；Sk为V2H状态，0表示车辆出网，1表示车辆入网；td为车辆出网时刻；ta为车辆接入家庭用电网时刻。

3 V2H系统二次规划模型

在考虑分时电价以及分时用电需求的条件下，以用电成本最小为控制目标，构造V2H二次规划模型，标准二次规划模型为

(8)

式中：x为决策变量；向量和矩阵Q、R、A、b、Aeq、beq为标准二次规划参数。

根据前面所述系统模型得到以下二次规划目标函数、等式约束以及不等式约束。目标函数为

(9)

式中J为日用电总成本。

不等式约束为

(10)

式中：SOCmin和SOCmax分别为荷电状态最小值和最大值；Imin和Imax分别为电池组充放电电流最小值和最大值。

等式约束为

(11)

式中：SOC0为初始荷电状态；SOCm为目标荷电状态。

本文以电流Ik和SOCk为二次规划数学模型的决策变量x，其表达式为

x=[I0,I1,…,IN-1,SOC0,SOC1,…,SOCN]T。

(12)

根据公式(9)—(11)，分别得到向量和矩阵Q、R、A、b、Aeq、beq的表达式为：

Q=diag([2RintΔtc0S0,2RintΔtc1S1,…,

2RintΔtcN-1SN-1,0,…,0])

(13)

R=[VocΔtc0S0,VocΔtc1S1,…,

VocΔtcN-1SN-1,0,…,0]T

(14)

(15)

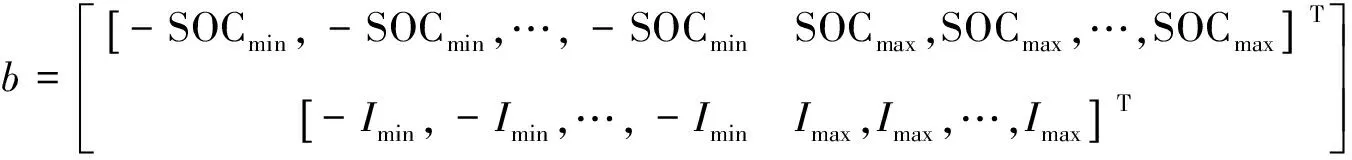
(16)

(17)

beq=[0,0,…,0,SOC0,SOCmax]T。

(18)

模式A、模式B和模式C的不同在于当电池组接入电网进行充放电时，3种模式的最小控制电流不同，模式A电池组仅充电不放电，即

Imin=0。

(19)

模式B电池组放电只为家庭用电提供电量，电池组充放电功率与家庭用电功率需求之和不得小于0，即：

Pbatt,k+Pdem,k≥0，

(20)

从而得到模式B电池组充放电电流最小值

(21)

式中Ibatt,min为电池组允许的最小充放电电流。

模式C电池组可以放电反馈回电网，即

Imin=Ibatt,min。

(22)

将不同模式最小电流带入V2H二次规划数学模型，通过Matlab二次规划求解器“quadprog”计算，即可得到不同模式的仿真结果。

4 仿真分析

假设一天中，车辆从00:00 到 08:00和 18:00 到24:00入网可进行充放电；从08:00到8:30车辆出网行驶一个UDDS工况；从08:30到17：30车辆出网停在停车场，且不充电；从17:30到18:00车辆出网行驶一个UDDS工况。原UDDS工况全程约为12km，持续22.85min。为了方便分析，使用修改后的UDDS工况，全程仍约为12km，持续时间为30min(在原UDDS工况末增加7.15min车速为零的工况)，修改后的UDDS工况和某车辆随工况的功率需求如图3所示。假设电动汽车电池组容量为24Ah，车辆08:00出网时的SOC为0.95，从08:00到08：30行驶一个UDDS工况后电池组SOC为0.815 1，从17:30到18:00行驶一个UDDS工况后电池组SOC为0.680 1。运行工况UDDS时SOC的变化曲线如图4所示。

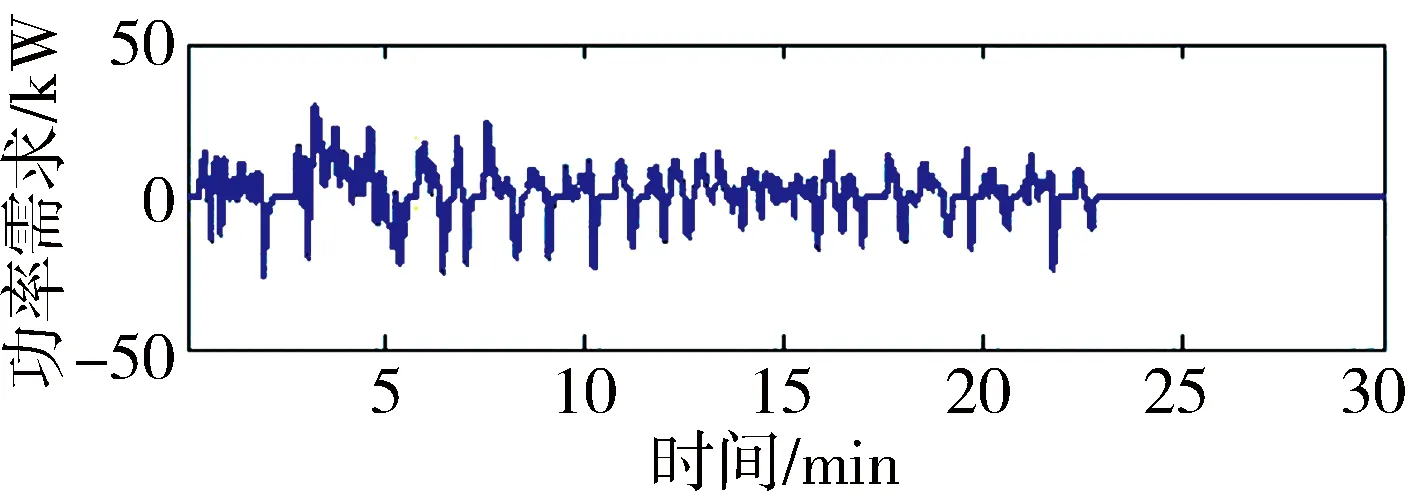
图3 车辆在UDDS工况中的功率需求

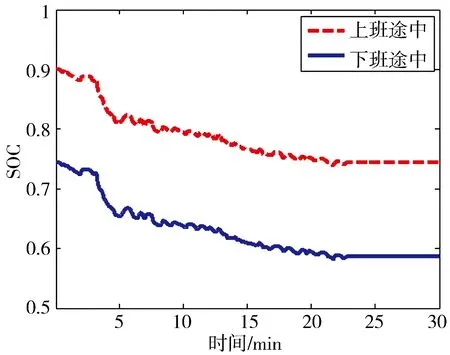
图4 运行UDDS工况SOC变化曲线

本文假设分时电价以及家庭分时电量功率需求如图5所示。

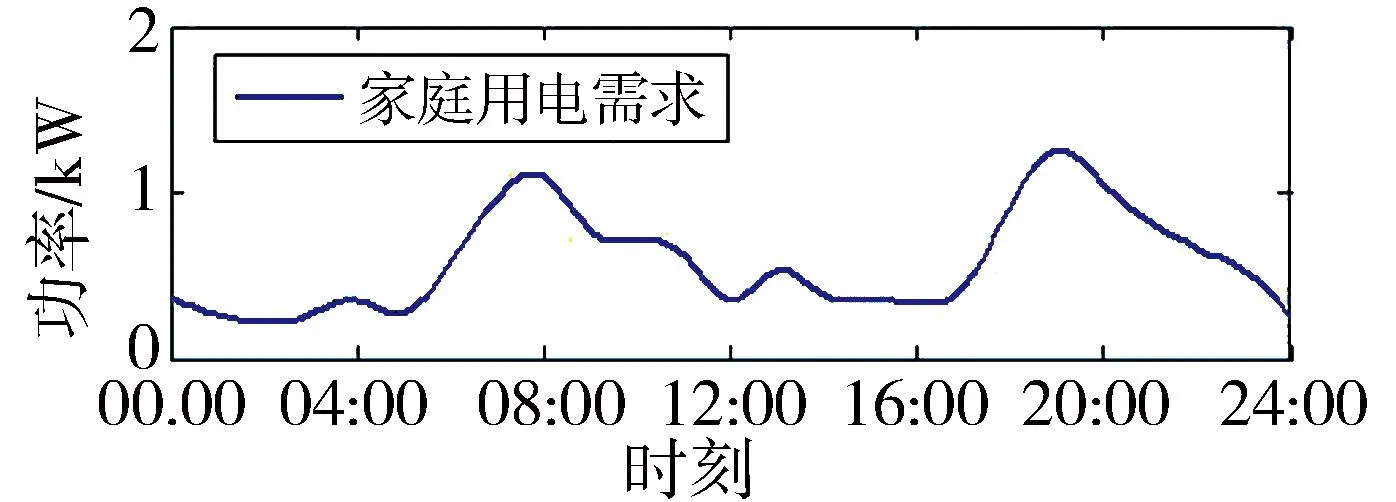
图5 分时电价和分时家庭用电需求

运用二次规划模型分别仿真分析从00:00到 08:00和18:00到24:00车辆入网后，模式A、B、C中电池组充放电电流和SOC随时间的变化，以及V2H系统功率以及用电成本随时间的变化。

主要仿真参数为：Δt =15min, Qcap= 24Ah, Voc=345V, Rint= 0.11Ω,SOCt=00:00=0.2,SOCt=24:00= 0.7,SOCmin= 0.1,SOCmax= 0.95, Ibatt,min=-9.6A, Imax= 9.6A。以模式C电池组入网充放电可放电反馈回电网为例，仿真结果如图6、图7和图8所示。

图6示出模式C电池组充放电电流和SOC随时间变化曲线。当车辆入网时，SOC和电流为经二次规划模型计算所得。当车辆出网时电流默认为0；SOC从08:00到8:30和17:30到18:00跟随UDDS工况变化，从08:30到17:30保持不变。UDDS工况中采样时间间隔Δt为1s，局部放大SOC变化曲线如图6所示。

图6 模式C电池组充放电电流和SOC曲线

图7 示出模式C家庭用电功率、电池组充放电功率(出网时默认为0)以及电网提供功率随时间变化曲线。可以看出：在车辆入网的情况下，若电价比较便宜，电池组进行充电；若电价比较高，电池组放电为家庭用电提供电量，从而达到降低用电成本的目的。

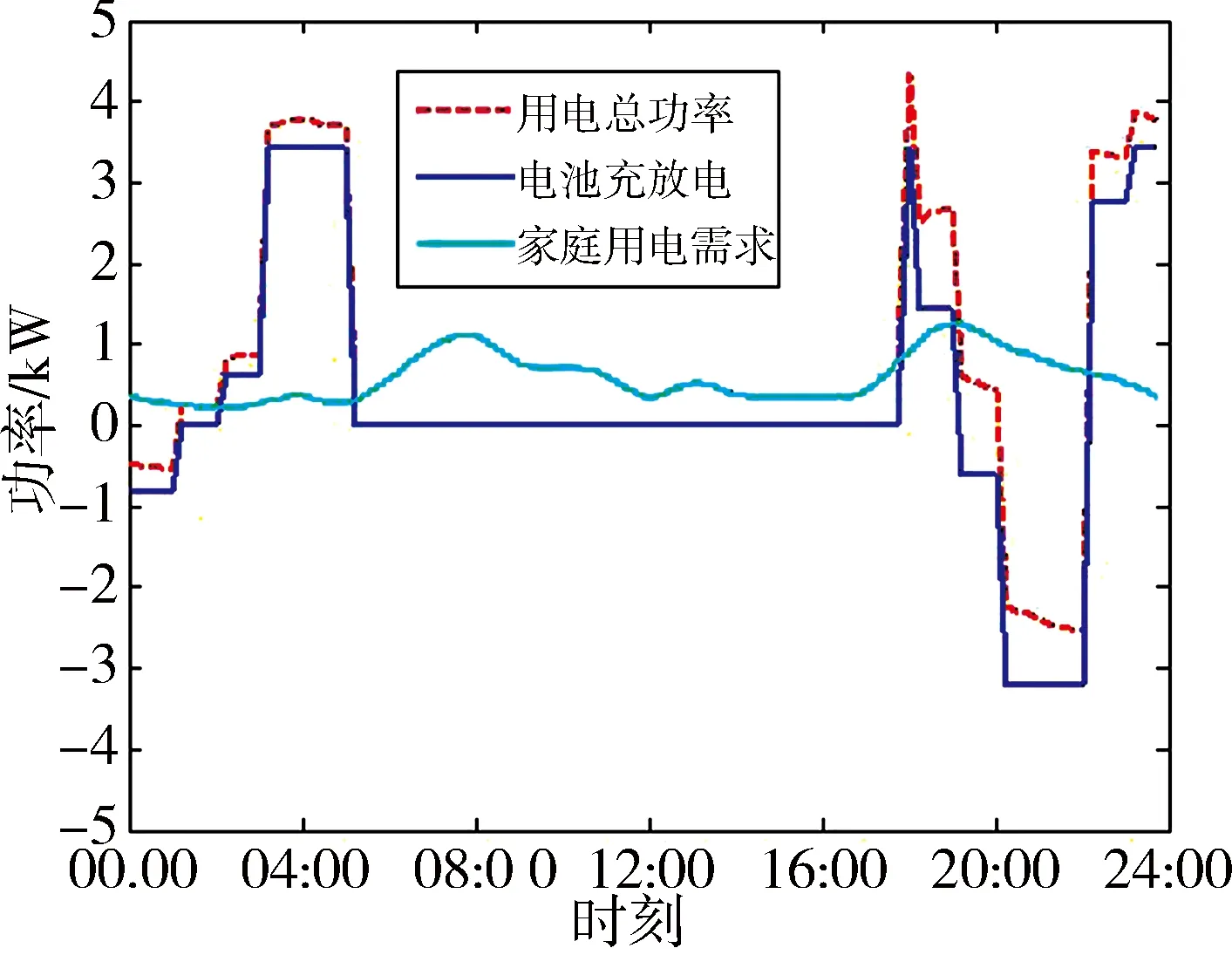
图7 模式C中V2H系统功率

图8示出模式C电网供电分时成本、电池组充放电分时成本和家庭用电分时成本曲线。其中；电网供电总费用为8.48元；家庭用电总费用为9.17元；电动汽车电池组充放电总费用为-0.69元(其中充电费用为6.59元，放电费用为-7.28元)。

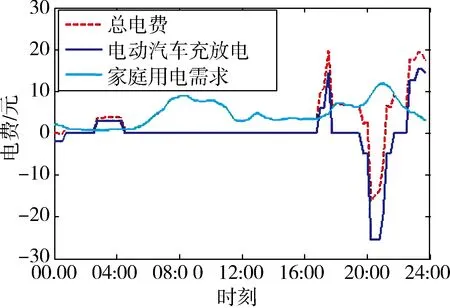
图8 模式C用电成本

使用二次规划模型仿真分析模式A、B、C，得到不同控制模式下电网供电总费用、电动汽车电池组充放电总费用和家庭用电总费用如表1所示。可知：使用二次规划模型的模式A、B、C比电动汽车即插即充模式的用电成本分别减少8.05%、16.81%、24.96%；模式B和模式C相对于模式A可分别减少用电成本9.53%和18.38%。基于二次规划优化控制的V2H系统可以有效地降低日用电成本。

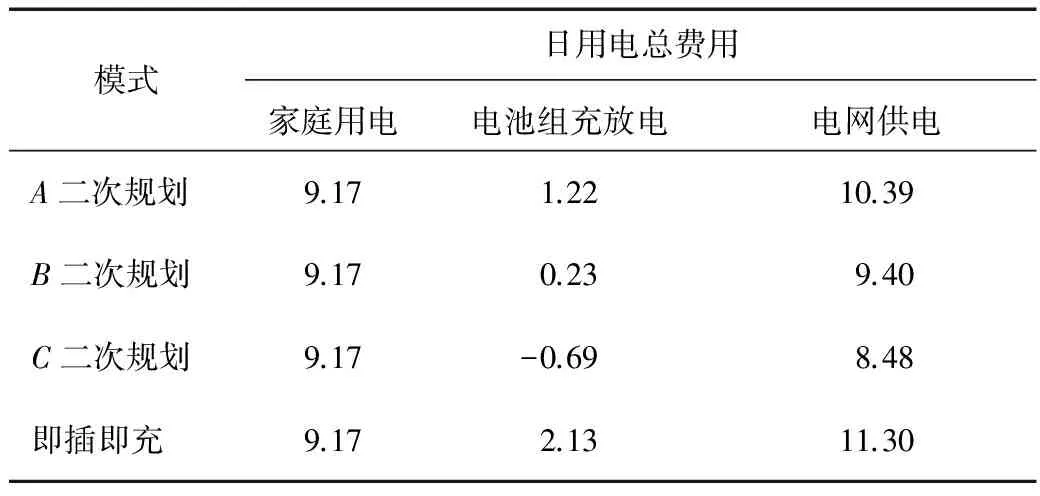
表1 不同工作模式的用电成本 元

5 结束语

车辆接入家庭用电网系统中，电动汽车电池组可以根据分时电价以及家庭用电需求对电池组充放电电流进行优化。本文首先分析了V2H系统结构和工作模式，建立V2H系统电池模型、功率流模型和用电成本模型，确定了以用电成本最小为优化目标的V2H系统二次规划数学模型，定量分析了优化算法对用电成本的影响。考虑车辆出行随机性、分时家庭用电需求随机性、可再生能源随机性等信息，进一步综合考虑以用电成本最小、电池寿命及健康状态最佳为优化目标，发展更有效可行的多目标优化控制算法将是下一步需要研究的问题。

[1]葛少云，王龙，刘洪,等. 计及电动汽车入网的峰谷电价时段优化模型研究[J]. 电网技术，2013,37(8)：2316.

[2]李惠玲，白晓民．电动汽车充电对配电网的影响及对策[J]．电力系统自动化，2011，35(17)：38．

[3]王锡凡，邵成成，王秀丽，等. 电动汽车充电负荷与调度控制策略综述[J].电机工程学报，2013，33(1):1.

[4]胡泽春，宋永华，徐智威，等.电动汽车接入电网的影响与利用.电机工程学报，2012, 32(4):1.

[5]罗卓伟，胡泽春，宋永华，等．电动汽车充电负荷计算方法研究[J]．电力系统自动化，2011，35(14):36.

[6]Duong Tung Nguyen，Long Bao Le. Joint Optimization of Electric Vehicle and Home Energy Scheduling Considering User Comfort Preference[J]. IEEE Transactions on Smart Grid, 2014, 5(1):188.

[7]Chengke Zhou, Kejun Qian, Malcolm Allan,et al. Modeling of the Cost of EV Battery Wear Due to V2G Application in Power Systems[J]. IEEE Transactions on Energy Conversion, 2011, 26(4):1041.

[8]Pia Grahn, Joakim Munkhammar, Joakim Widén, et al.PHEV Home-Charging Model Based on Residential Activity Patterns[J]. IEEE Transactions on Power System, 2013, 28( 3):2507.

[9]罗卓伟，胡泽春，宋永华，等．大规模电动汽车充放电优化控制及容量效益分析[J]. 电力系统自动化, 2012, 36(10): 19.

[10]Clement-Nyns K，Haesen E，Driesen J．The Impact of Charging Plug-in Hybrid Electric Vehicles on a Residential Distribution Grid[J]．IEEE Trans. on Power Systems，2010，25(1)：371．

[11]Ryuichi YOKOYAMA， Kouichirou YOSHIMI1 ， Takahiko MASUDA, et al. Contribution of Electric Vehicles for Energy Management in Smart Houses with Uncertain Power Generation[J]. Automation of Electric Power Systems, 2011, 35(22): 18.

[12]Wu Zhi, Zhou Suyang, Li Jianing, et al. Real-Time Scheduling of Residential Appliances via Conditional Risk-at-Value[J]. IEEE Transactions on Smart Grid, 2014,5(3):1282.

[13]Kristien Clement-Nyns, Edwin Haesen, Johan Driesen. The Impact of Charging Plug-In Hybrid Electric Vehicles on a Residential Distribution Grid[J]. IEEE Transactions on Power System, 2010,25(1):371.

[14]Scott J Moura, Jeffrey L Stein, Hosam K. FathyBattery-Health Conscious Power Managementin Plug-In Hybrid Electric Vehicles viaElectrochemical Modeling and Stochastic Control[J]. IEEE Transactions on Control Systems Technology, 2013, 21(3): 679.

[15]胡晓松.电动车辆锂离子电池模型辨识、优化与状态估计[D].北京：北京理工大学，2012.

(编校：夏书林)

Charging and Discharging Control Strategy for Home with Plug-in Electric Vehicle Based on Quadratic Programming

WU Xiaohua1, YIN Xiaofeng1, CHEN Zeyu2, ZHANG Long1

(1.School of Transportation and Automotive Engineering,Xihua University, Chengdu 610039 China;2.CollegeofMechanicalEngineeringandAutomation,NortheasternUniversity,Shenyang110819China)

In this paper, vehicle to home (V2H) system is the research object. Firstly, the system structure and main operating modes of V2H are proposed. The mathematic models of batteries, power flow of V2H system and electricity costs are fabricated. Based on time-varying electricity price and time-varying power demand of home, the quadratic programming V2H system optimization control strategies are designed to minimize the total daily electricity cost. In mode C, for example, variations of batteries SOC, charging and discharging current, V2H system power flow, electricity costs were analyzed in a whole day. Finally, comparative analysis of electricity costs based on quadratic programming optimal control in three main V2H modes was obtained. The result shows that quadratic programming optimal control for V2H can effectively reduce electricity costs.

vehicle to home(V2H); charging and discharging optimization; quadratic programming(QP); plug-in electric vehicle.

2015-10-13

四川省科技厅应用基础项目(2013JY0088)；四川省青年科技创新研究团队专项计划项目(2015TD0021)；国家自然科学基金(51375402)；四川省教育厅项目(12ZB320)；西华大学基金项目(Z1220315)；汽车工程四川省高等学校重点实验室开放研究基金项目(SZJJ2012-012)。

武小花(1984—)，女，讲师，博士，主要研究方向为电动汽车整车控制及多动力耦合技术。

U469.72+2

A

1673-159X(2016)05-0001-6

10.3969/j.issn.1673-159X.2016.05.001