基于梯度边缘最大值的图像清晰度评价

刘亚梅

(长春工业大学机电工程学院，吉林 长春 130021)

Liu Yamei

(Changchun University of Technology Institute of Electrical and Mechanical Engineering, Changchun Jilin 130021, China)

基于梯度边缘最大值的图像清晰度评价

刘亚梅

(长春工业大学机电工程学院，吉林 长春 130021)

光电遥感相机获取的遥感图像传回地面后都会出现一定降质模糊现象，通过复原可以得到较高质量的遥感图像。得到复原图像后，需要一些方法来评价复原图像质量提高的程度。为此提出了一种遥感图像清晰度的评价方法，通过提取图像的梯度，找出梯度最大的区域，计算出该区域的像元个数，并以此作为图像的清晰度参数，计算复原图像清晰度与降质图像清晰度之间的相对误差，得到清晰度提升率。通过设计实验来验证该方法的有效性。结果表明，该方法可以准确评估复原图像的清晰度提升率，对弱振铃波纹有较好地抑制效果，在信噪比大于22 dB时，评价结果不受噪声影响。

图像质量评价；图像清晰度；遥感图像；梯度；信噪比

Liu Yamei

(Changchun University of Technology Institute of Electrical and Mechanical Engineering, Changchun Jilin 130021, China)

空间光学遥感器在越来越多的领域中得到应用，如国土资源考察、自然灾害监测等。然而，由于光学成像系统离焦、星载平台振动、大气湍流及目标相对于相机的运动等原因，会使图像产生模糊或边界不清晰等降质问题[1]。目前在空间载荷的条件下提高图像质量的方法是对图像复原。复原系统输出的复原图像相对于降质图像，其质量是否得到了提高，需要采用一系列评价方法来评估。图像复原后清晰度、对比度、信噪比(signal noise ratio, SNR)等指标均会发生变化。图像的细节信息越充足，图像灰度变化越快，则图像越清晰，人眼视觉分辨程就度越高，清晰度指标更适合分析图像质量，本文将对复原前后图像的清晰度变化程度作质量评估。

清晰度评价通常有梯度函数法、统计学法、频谱函数法、熵函数法等[2]。此外，倪军等[3]、赵剡和杨威[4]、张天煜等[5]通过统计图像边缘的宽度信息来计算图像的清晰度，边缘越宽，则图像越模糊，清晰度越低；曹茂永等[6]计算了灰度图像梯度向量的模方和，利用Roberts梯度和，Laplace算子和来评价离焦模糊图像清晰度；李从利等[7]提出了基于码书的雾天图像质量评价方法，能够延伸到离焦模糊图像评价上来；林莹等[8]提出了一种基于形态学梯度的灰度图像清晰度评价算法，通过形态学结构元素计算灰度图像的梯度信息，将梯度信息叠加后得到图像的形态学梯度边缘，利用其信息作为图像清晰度评价的测度。但是这些函数并没有将表征噪声与图像边缘的信息准确分离，评价结果受噪声的影响很大。为此，需要寻找一种方法，能够最大限度抑制噪声，降低振铃波纹等因素对清晰度评价结果造成的影响。

本文提出了一种可以抑制噪声与振铃波纹干扰的半参考清晰度评价方法，并能评价遥感图像复原后的清晰度的提升率。

1　原理分析

图像的边缘是表征图像特征的一个重要信息，理想的边缘具有阶跃模型的特性，然而对于自然图像，成像过程的不完善使图像边缘具有一个过渡区的倾斜面，表现为图像模糊。图像的边缘情况可以反映图像的清晰程度：图像越清晰，边缘位置的灰度变化越大；反之，越模糊的图像，过渡区倾斜越大，利用图像边缘的梯度来评价图像的清晰度是可行的[3-4]。

一个图像的梯度图信息可用以下模型[9]来表述：f表征一幅灰度图集合，e为灰度图的像元，e∈f，m是f上的一个测度，用以计算f上每个像元e的梯度，图像的梯度幅值集合G如下：

图像的梯度受噪声及失真干扰大，振铃效应也会对图像的总体梯度产生影响，在这些情况下，G所包含的内容既有原图像的梯度，还包括其他干扰的梯度信息，可用下式来表示：

其中，Gk为图像梯度的集合、噪声梯度的集合、振铃波纹梯度的集合等，这些子集最终组成了整幅图像的梯度集合。

图像越模糊，其边缘越不明显：

其中，S1为模糊程度较大的图像边缘区域集合，S2为模糊程度较小的图像边缘区域集合，|S|表示图像边缘区域集合的势。

当噪声与振铃波纹较小时，通常，噪声与振铃的梯度值远小于图像边缘位置的梯度值，满足以下式子：

其中，B为图像梯度集合S中的元素，即梯度图像对应的像素值为：

其中，Bnoise为噪声梯度集合中的元素，Bringing为振铃波纹梯度集合中的元素，Bedge为图像边缘梯度的集合中的元素，T为某一阈值。

在满足式(5)的情况时，选取一个较大的阈值T，以梯度值大于T的区域作为梯度最大值区域Smax。

根据式(3)可知：

其中，S1max为模糊图像的梯度最大值区域集合，S2max为清晰图像的梯度最大值区域集合，|Smax|为梯度最大值区域的势。由式(7)可知，以复原前后图像的梯度最大值区域的势来表示图像清晰度是可行的。

图1为一幅遥感图像的原图和梯度图以及对原图进行模糊后提取的梯度图。

图1　遥感图像原图及梯度图

图像越模糊，其对应梯度图中梯度值大的区域越少。图像的清晰度可根据梯度最大值区域的势来评价，对于同源图像，越模糊，其梯度最大值信息含量越少，计算梯度最大值区域的势，作为图像清晰度的参数，将复原图像与降质图像的清晰度参数进行对比，计算复原图像与降质图像清晰度之间的相对误差，得到清晰度提升率。

2　图像清晰度提升率算法

算法流程如图2所示。

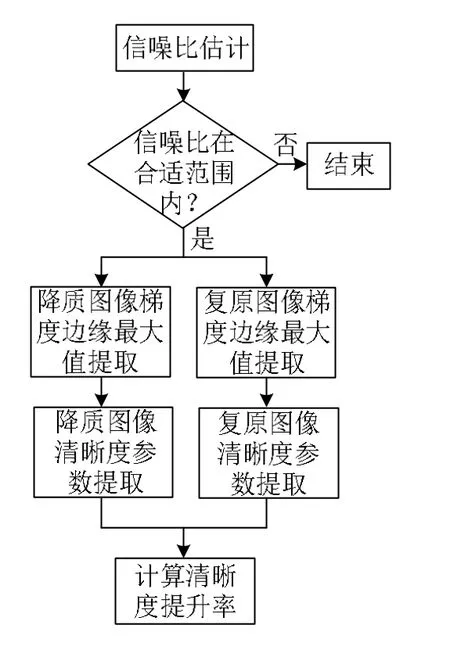
图2　算法流程图

2.1信噪比估计

当噪声过大时，噪声的梯度将会增大，即Bnoise的值会增大，当 Bnoise增大到不能满足式(5)的情况时，该算法不再有效。因此，在进行图像清晰度评估前，应对图像进行SNR估计。

本文采用文献[10]中的SNR估计算法。图像的SNR定义：

在图像的平坦区域与边缘区域有不同的方差，图像f在位置(i, j)处的局部方差为：

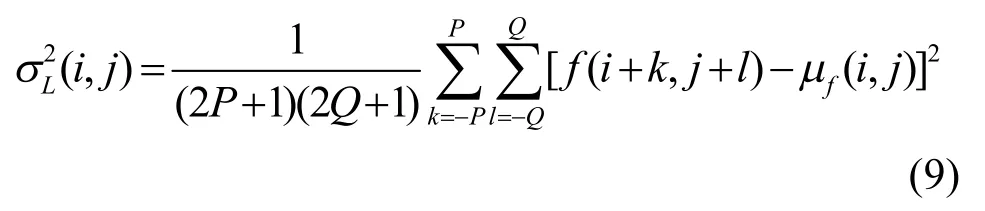
其中，μf为局部均值，

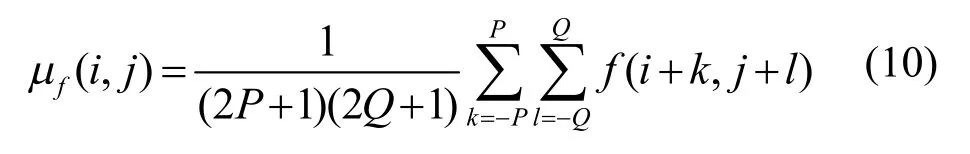
局部方差窗口尺寸：P=Q=2(5×5窗口)。近似的SNR估计算法：利用式(9)计算图像的局部方差，用图像局部方差的最大值和最小值之比作为图像的SNR估计。

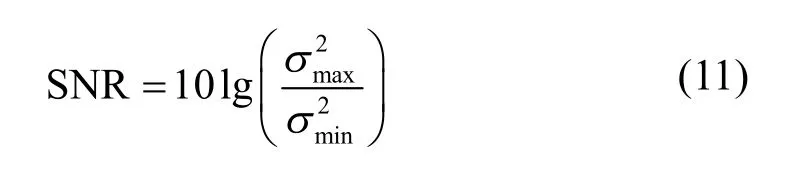
如文献[9]所述，使用该方法估计出的SNR小于20 dB时，则该图像受噪声影响过于严重，无法进一步处理。

2.2基于梯度算子的梯度边缘确定

常用的梯度算子有Sobel算子、Prew itt算子、Roberts算子、拉普拉斯高斯算子(laplacian of Gaussian, LOG)等，几种算子的模板如下：

Sobel算子：

根据以上3种算子求出了x与y方向上的梯度，图像总梯度根据式(1)求得，求取x与y方向上的梯度平方和再开方得到最终梯度值。

LOG算子：

图3为4种算子提取出来的梯度图，从图4可看出，LOG算子放大了图像中的噪声信息，且提取的梯度非常混乱。而 Sobel算子、Prewitt算子和Roberts算子均能对梯度信息进行较好检测，但是Roberts算子提取的梯度值较小，不能很好地反映灰度变化大小，Sobel算子在提取梯度时将各个边缘都放大了，在一定程度上也放大了噪声，用Prewitt算子提取出的梯度图像不仅能很好地反映图像的边缘信息，其对噪声的放大能力也低于 Sobel算子，可以较好地减轻噪声产生的影响。在本文中，选择Prewitt算子进行计算。

图3　不同梯度算子提取的梯度图

图4　降质图像与复原图像

2.3图像清晰度提升率计算

根据第 1节的分析，若图像满足式(5)时，可选择一个合适的阈值T，即选取梯度最大值范围，将大于梯度阈值的像素做标记：

阈值的选取与图像大小不相关，且需要具有通用性，在梯度图中，对于双精度类型图像，表征边缘区域的像素值通常都大于1，因此，取阈值T=1。

根据式(7)可知，模糊图像的梯度最大值集合的势小于清晰图像梯度最大值集合的势，因此，统计两个集合中的元素个数作为清晰度参数。

统计标记过的像素个数，即集合 M中的元素个数作为集合M的势，得到的值Q作为图像的清晰度参数：

降质图像的清晰度用 Q1表示，复原图像的清晰度用Q2表示。

最终复原图像相对于原降质图像的清晰度提升率可用下式表示：

η越大，图像清晰度越高。如果η小于0，说明图像清晰度没有得到提高，图像复原失败。

3　实验及数据分析

3.1清晰度提升率计算

选取如图4所示的9组遥感图像并对其做复原处理，每组图像前一幅为原始图像，后一幅为复原后的图像。对降质图像及复原图像利用 Prew itt算子作梯度图，统计梯度值大于 1的像元个数作为图像的清晰度参数 Q，利用式(18)计算清晰度提升率。

分别对 9组图像利用拉普拉斯能量(energy of Laplacian, EOL)、灰度平均梯度(gray mean gradient, GMG)和文献[3]的方法，结合式(18)计算清晰度提升率，并与本文结果作比较。对9组图像加入均值为0，方差为0.002的高斯白噪声，使用同样的方法计算加噪后图像的清晰度提高率，对比结果如表1所示。

表1　图4各组数据计算清晰度提升率

该算法对图像清晰度参数值敏感，从评价结果来看，能够得出复原图像的清晰度相对于降质图像的清晰度提高的结论，与主观观察结果一致，评价结果良好。相对于其他算法，本文方法的评价结果具有很强地抗噪声能力，评价结果几乎不随噪声的加入而发生较大变化。

3.2算法对弱振铃边界的抑制作用

对图像进行复原处理时，PSF估计不准确会导致图像边界产生振铃波纹，振铃波纹的出现会对边界提取产生干扰，从而导致清晰度参数估计的不准确，因此，在设计算法时应考虑算法对振铃波纹的抑制作用。

当图像满足式(5)时，即振铃波纹的梯度极大值小于图像边缘的梯度极大值，该振铃波纹强度较弱，在提取梯度最大值后，弱振铃波纹的影响可以被消除。

从图5可看出，对弱振铃波纹，梯度图能够将其提取出来，但弱振铃波纹的梯度不在梯度最大值范围内，梯度最大值的选取可以抑制弱振铃波纹对清晰度参数的影响。

图5　对振铃波纹的抑制作用

3.3算法抗噪声性能实验及分析

在进行边缘检测时，与图像边缘同处于高频段的噪声容易被误认为是边缘目标而影响到清晰度参数的估计。算法对噪声的抑制程度决定了清晰度参数估计的准确性。本节讨论本文算法对图像噪声的抑制能力。

选取图4(1)，分别对降质图像与复原图像加上一系列高斯噪声，采用2.1中的方法对加入噪声的图像进行 SNR估计。再使用本文的方法进行图像清晰度参数提取。

由图6可看出，在SNR低于22 dB时，图像清晰度参数提取值较大且不稳定，这是由于 SNR过低时，噪声对图像边缘产生了较大影响，因此在进行清晰度评判之前，应先对图像进行 SNR判断，SNR过低的图像不能进行分析及处理。

散点图在SNR大于22 dB 时近似于一条平稳的直线，图像总体的清晰度参数表现平稳，稳定性好，受噪声影响不大，复原图像与降质图像的清晰度参数能够很好地分辨出来。

该算法具有良好的抗噪声性能。

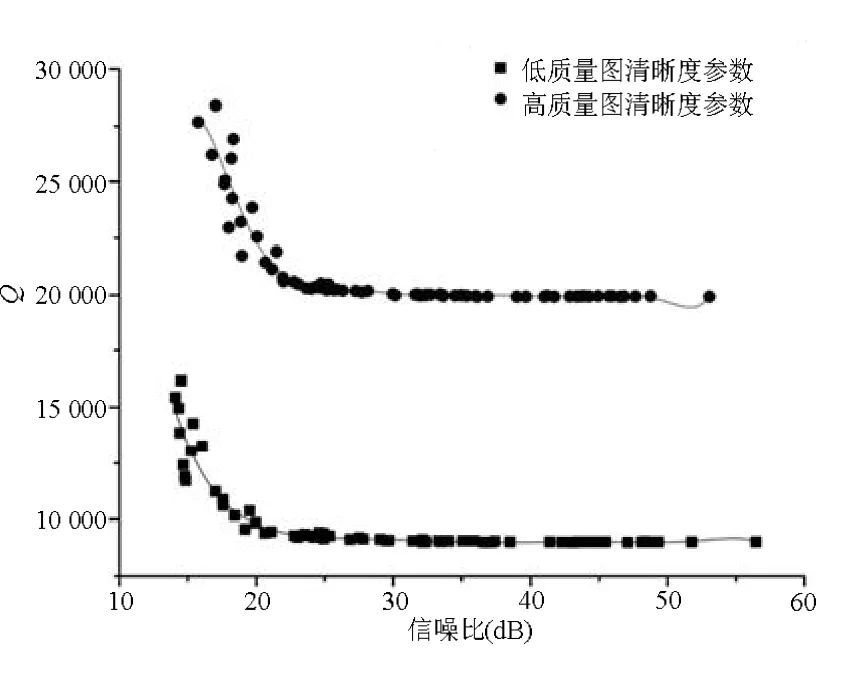
图6　图像清晰度参数随信噪比的变化情况

4　总　结

本文深入分析了图像梯度边缘最大值与清晰度的关系，以图像梯度边缘最大值区域的势作为图像的清晰度参数，并以此计算复原图像相对于降质图像清晰度提升率的大小。对比不同的边界提取算子对实验结果的影响，最终确定选取Prew itt算子进行梯度边缘最大值提取，算法可以抑制弱振铃波纹，且具有良好地抗噪声性能，并能够在较宽的SNR范围内进行评估，在SNR大于22 dB时，评价结果不受噪声的影响。实验结果表明，该方法能够很好地评估图像清晰度变化情况，且具有良好地抗噪声性能与抑制振铃能力。

[1] 杨利红. 大视场航天相机遥感图像复原研究[D]. 长春:中国科学院研究生院, 长春光学精密机械与物理研究所, 2012.

[2] 李祚林, 李晓辉, 马灵玲, 等. 面向无参考图像的清晰度评价方法研究[J]. 遥感技术与应用, 2011, 26(2): 239-246.

[3] 倪军, 袁家虎, 吴钦章. 基于边缘特征的光学图像清晰度判定[J]. 中国激光, 2009, 36(1): 172-176.

[4] 赵剡, 杨威. 一种基于边缘特征的图像质量评价新方法[J]. 红外与激光工程, 2006, 35(增刊): 232-238.

[5] 张天煜, 冯华君, 徐之海, 等. 基于强边缘宽度直方图的图像清晰度指标[J]. 浙江大学学报: 工学版, 2014, 48(2): 312-320.

[6] 曹茂永, 孙农亮, 郁道银. 离焦模糊图像清晰度评价函数的研究[J]. 仪器仪表学报, 2001, 22(3): 259-260, 268.

[7] 李从利, 陆文骏, 石永昌, 等. 基于码书的雾天图像质量评价方法研究[J]. 图学学报, 2014, 35(6): 876-882.

[8] 林莹, 张兆东, 刘景夏, 等. 基于形态学梯度的灰度图像质量盲评价[J]. 计算机应用与软件, 2012, 29(1): 264-266.

[9] 冈萨雷斯, 伍兹, 艾丁斯. 数字图像处理(MATLAB 版)[M]. 北京: 电子工业出版社, 2007: 80-82.

[10] 邹谋炎. 反卷积与信号复原[M]. 北京: 国防工业出版社, 2001: 137-139.

Sharpness Assessment for Remote Sensing Image Based on M aximum Gradient

The image acquired by the remote sensing camera w ill appear to be a certain fuzzy phenomenon after transmitted it to the ground. It w ill get high quality image after restoration, and it is necessary to use some methods to assess the quality of recovery image. This paper proposes a sharpness assessment for remote sensing image, which picks up gradient from images, calculates the number of the pixels on the region of maximum gradient and the data is used as sharpness parameter. We get the upgrade rate after comparing the sharpness parameters between the fuzzy image and the recovered image. We demonstrate the validity of this new method through some experiments. The experimental results show that the method can accurately assess the sharpness upgrade rate of the restored image, and get better results in the inhibiting effect of weak ringing ripples and the anti-noise performance when the signal noise ratio over 22 dB.

image quality assessment; image resolution; remote sensing image; gradient; signal noise ratio

TP 751.1

10.11996/JG.j.2095-302X.2016020237

A

2095-302X(2016)02-0237-06

2015-08-24；定稿日期：2016-01-19

刘亚梅(1970–)，女，吉林长春人，高级实验师，硕士。主要研究方向为图像处理。E-mail：liuyamei2004@126.com