基于数据类型转换的点云快速有损压缩算法

律　帅， 达飞鹏， 黄　源

(东南大学自动化学院，江苏 南京 210096)

基于数据类型转换的点云快速有损压缩算法

律帅， 达飞鹏， 黄源

(东南大学自动化学院，江苏 南京 210096)

针对海量三维点云数据为计算机存储和传输增加沉重负担的问题，提出一种基于数据类型转换的点云快速有损压缩算法。首先设计出一种数据类型转化规则-FtoI规则，根据 FtoI规则将浮点数类型点云转换成整数类型点云，然后将整数类型点云切分成许多小单元面块，每一单元点云生成最小生成树，按广度优先的顺序对树形结构进行编码。同时，按照树形结构对父子节点的差值进行编码，把整型差值分成两部分编码，符号一部分，其绝对值一部分，其中绝对值部分采用算术编码进行压缩。实验表明该文算法在保证整个三维点云模型的质量情况下，具有不错的压缩速度和压缩率。

三维点云；有损压缩；浮点数；最小生成树；算术编码

点云数据是物体三维扫描后其三维坐标的数据信息，还可能记录了RGB、深度等信息。随着三维扫描系统精度和速度的提升，扫描后点云数据量将达到几百万甚至更大的数量级，对其网格化的时间开销增大，网格化模型的内存开销也随之增大，管理操作网格拓扑信息存在诸多问题，计算机在处理多边形网格模型的复杂度急剧增加；此外，当多边形网格模型在屏幕中网格数量大于屏幕分辨率时，用点作为模型数据的基本单元比多边形网格有更加明显的效率优势。因此基于点的图形学在1985年，由Levoy和Whitted[1]提出，并逐渐成为计算机图形学的研究热点[2-4]。目前，海量点云数据为计算机存储和传输增加沉重的负担，因此研究点云数据的压缩具有重要的意义。

点模型压缩通常由顶点数据压缩和属性数据压缩[5]两部分组成，本文压缩算法主要针对点模型的顶点数据进行压缩。点模型数据的压缩根据接收数据的方式通常分为2种：渐进式压缩和单分辨率压缩，渐进压缩是低精度的粗网格模型，是从边传送边显示精细细节信息，需要构造多分辨率的层次结构，导致数据冗余，从而影响数据压缩效果，何辰[6]的基于形状分析的三维点云模型压缩方法是渐进压缩方法中一个典型的代表。点模型的单分辨率压缩只接受整个点模型数据后才进行压缩编码，相对于渐进压缩有较高压缩率，缺点是时间效率较低，如Gumhold等[7]的压缩编码算法。同时点模型数据的压缩根据能否完整的还原点云数据分为无损压缩和有损压缩，其中无损压缩如王鹏杰等[8]的基于局部最小生成树的快速无损压缩算法，算法有较高的时间效率。由于无损压缩率较低，多数点云压缩算法都是有损压缩，点云模型去除一部分点云也可以很好地保留物体的三维信息[9-10]，同时点模型的位置坐标信息都是用浮点数表示，浮点数表示的精度很大，在工程实践中不需要很高的精度，可以降低浮点数精度，总体来说有损压缩在压缩率上要优于无损压缩。

点模型数据压缩算法为了提高压缩率，需要在预测之后和熵编码算法进行有效的结合，如Chen 等[11]的算法由于没有与熵编码算法有效结合，得到的压缩率相对较低，而Isenburg等[12]提出了一种浮点数熵编码压缩算法，可以有效地提高点云数据的压缩率。

工程实践中对压缩实时性和压缩率的要求越来越高，因此本文提出一种基于数据类型转换的点云快速有损压缩算法，该算法是一种单分辨率点模型压缩算法，同时结合算术编码，有效地提高压缩率，实验结果表明该算法在保证整个三维点云模型的质量情况下，有着较高的压缩速度和压缩率，可以满足在工程实践中对实时性和高压缩率的要求。

1　点云压缩算法简介

本文点云压缩算法流程如图1所示。首先本文提出一种数据类型转换规则(float to integer, FtoI)，将浮点数转换成对应的整数，接着将整个模型分割成多个小块模型单元，对于点云模型切分的大小决定了点云数据压缩时间和压缩率的大小，单元切分的过大，导致最小生成树的时间开销过大，时间效率低，最大预测误差会增大，而单元切分的过小，会导致编码不连续性，使算法压缩率过低，下文实验证明单元点云数70为最佳。点云模型切分后，对每一单元再采用最小生成树算法，对点云数据进行预测，对于最小生成树树形结构采用算术编码进行编码压缩。对于整数类型的顶点数据，根据最小生成树，把子父节点的差值拆成两部分，符号位部分和绝对值部分，对绝对值部分进行算术编码压缩。

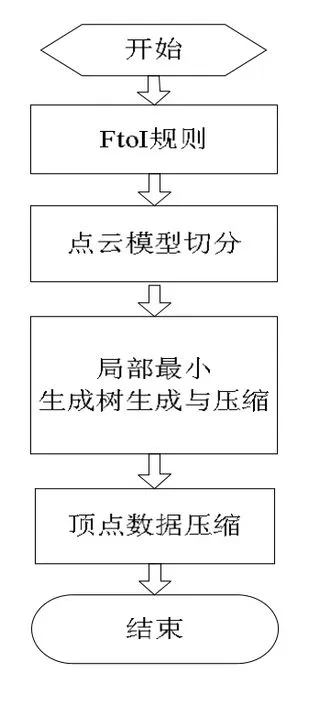
图1　算法流程图

2　点云有损压缩算法

2.1浮点数简介

现今计算机系统中普遍采用1985年IEEE协会发布的二进制浮点数算术标准(IEEE754)[13]，该标准定义了被广泛使用的32位二进制浮点数(单精度) 和64位二进制浮点数(双精度)的存储格式。单精度浮点数在计算机中的存储方式如图2所示，一个单精度浮点数可分为3部分：符号位(1 Bit)、指数位(8 Bit)、尾数位(23 Bit)。

图2　IEEE标准下浮点数存储方式示意图

任意二进制浮点数的数值由下式表示：

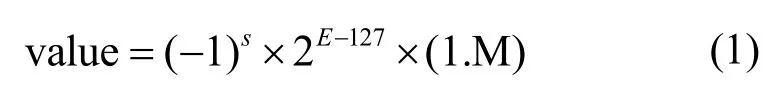
浮点数真实指数值e表示为：e=E-127。

图3为浮点数之间的符号位、指数位和尾数位关系图，横坐标为实数坐标轴，纵坐标为实数对应的浮点数，如图3所示，0.3、0.7和6.3、6.7的差值都是 0.4，但浮点数的尾数位差值分别为ox199999和ox0ccccc，表明在相同误差下，不同的指数段，尾数位差值是不同的，指数位越大，尾数位差值越小。

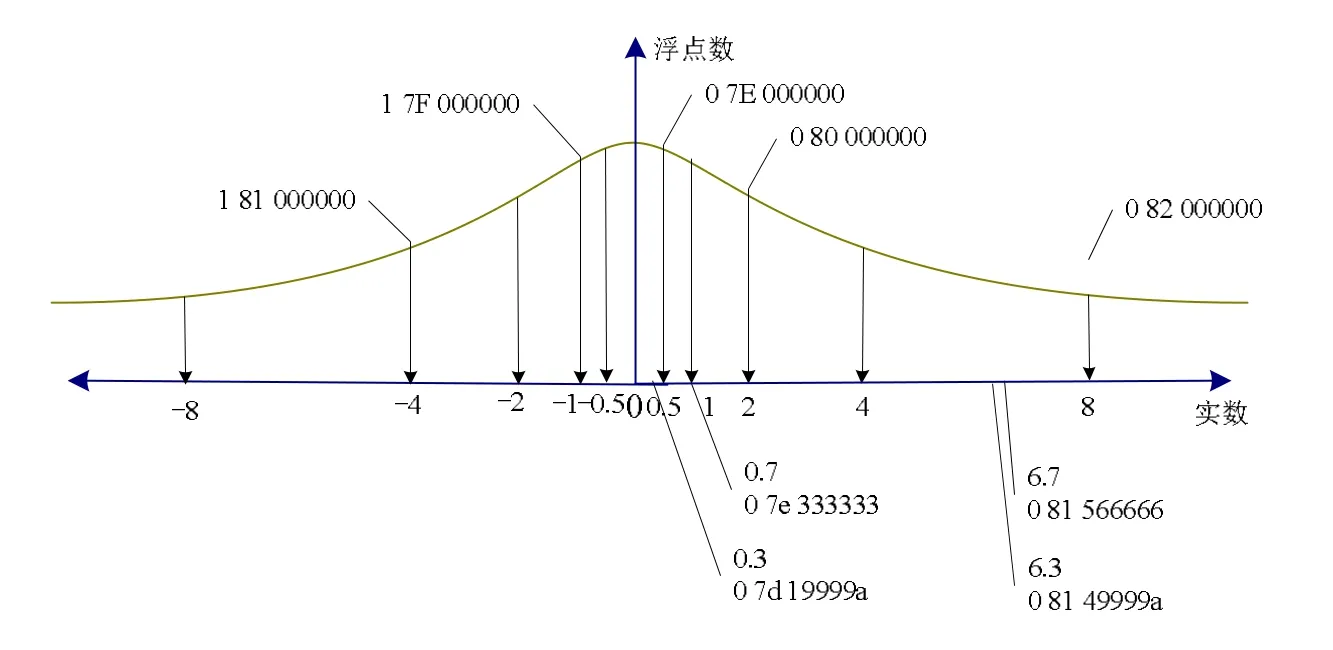
图3　浮点数符号位、指数位和尾数位关系图

2.2FtoI规则

对于点云的三维坐标信息，用浮点数表示，其指数位不尽相同，为了直观显示点云的指数位部分，图4是Bunny点云数据模型指数位的直观示意图，红绿根据x坐标方向浮点数的指数位变化而变化。根据浮点数的特点，其指数位不同，因此其精度也不相同，指数位越小，表示数值的精度就越高。对于一个点云模型的数据显示，各方向中指数位最大的坐标数据精度最低。

图4　点云模型指数位的示意图

如果点云的测量精度小于点云数据表示的最低精度，那么对于指数位低的高精度数据即多余的二进制数相当于估计值，没有实际意义，可以忽略不计。相反如果点云的测量精度大于点云数据表示的最低精度，虽然指数位低的数据比指数位大的数据对模型表示更加准确，但三维重建后[14]，模型与实际物体之间误差在指数位高的区域较大，在指数位低的区域较小，对于整个模型的质量来说由指数位高的区域决定。因此指数位较小的区域可以降低精度，使整个模型误差达到相对的平衡。

基于以上分析，对于指数位小的点云数据无需保留太高的精度，统一将点云数据转换成最大指数位的精度，设计出一种点云FtoI规则，将浮点数转换成对应的整数。

FtoI规则：

(1) 将点云x, y, z坐标浮点型数据，拆成符号位、指数位、尾数位3部分，其中x, y, z各坐标最大的指数位记为Exmax，Eymax，Ezmax。

(2) 各方向坐标系的数据，根据其指数位和最大指数位的差值dif，将尾数位最左端补加一个1，即尾数位变成24位，再右移dif位，将尾数位转换成整型。

(3) 整型数据符号位和对应的浮点数符号位相同。

FtoI规则将浮点数类型点云数据统一精度，然后转化成整数类型，浮点数和整数可以相互转化。FtoI规则会损失部分精度，但不会影响整个点云模型的质量，图 5(a)为原始点云模型，图 5(b)是经FtoI规则转换后的点云模型；图5(c)是原点云模型和 FtoI规则转换后的点云模型的合并模型，可以看出在中部有很少的绿色点云，表明原点云模型和规则转换后的点云模型几乎完全重合，只有中部存在少部分偏差，总体说明 FtoI规则不会影响整个点云模型的质量。浮点数转化整型有 2大优势：①整型数据运算相比浮点数效率高，提高时间效率；②转化后的整型数据相比浮点数去除了指数位的信息，有利于后续的压缩和保存，减少内存开销。

图5　Bunny点云模型

为了定量分析有损压缩后的模型与原模型的差别，本文提出点距误差比的概念记为kdis，即某点与其对应有损压缩点之间的欧几里得距离与该点与其最近点的欧几里得距离的比值。点与其对应有损压缩点之间的欧几里得距离记为diss，点与其最近点的欧几里得距离记为disr，则：

在图6中，a′点表示a点经过有损压缩后的点，b点表示离a点最近的点，a点的kdis为，当三维模型重建时，线段 ab是原模型上的一条线段，而线段a′b是有损压缩后模型上的一条线段，如果kdis比较小，说明ab和a′b越接近，有损压缩后的模型与原模型越接近。

图6　点距误差比示意图

把点云模型中点距误差比最大的称为最大点距误差比，所有点距误差比的平均值称为平均点距误差比，最大点距误差比和平均点距误差比越小，表明有损压缩后的模型与原模型越接近。

2.3点云模型切分

为了方便后续处理，需要对点云模型进行切分，首先利用八叉树算法进行粗切分，然后根据坐标轴依次切分。八叉树是一种三维数据结构，如图7所示，由Hunter[15]于1978年在其博士论文中首次提出，八叉树的主要优点在于可以非常方便地实现集合运算，有很强的空间分解能力，可以有效地处理大量的点云数据[16]，被广泛用于点云数据压缩中。

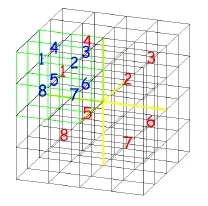
图7　八叉树简图

以下是八叉树切分算法：

(1) 记录点云在三维坐标中，各方向最大和最小值 Xmax，Xmin，Ymax，Ymin，Zmax，Zmin。以为中心，边长分别为最大值的最小立方体包围盒进行八叉树切分。

(2) 当八叉树父节点非空，且点云数量大于N，继续切分，否则停止切分，并设最大递归深度为depth，防止无穷切割。

(3) 重复步骤(2)，直至切分完毕或达到最大递归深度。

因为八叉树分割时无法保证每个叶节点内的点云数量符合要求，会出现很多碎片立方体，只含有很少点云，所以要进行适当的合并处理，本文采用同一个父节点内的点云x、y、z坐标排序的方法解决这种问题，具体步骤如下：

首先假设m个点云作为一组，则取N=50 m，而最大递归深度根据文献[17]分析，取 depth=20。对于一个点云模型八叉树切分后，每个节点内点云数量在50 m以下，对于点云数量m以下的节点合并到同一父节点相邻节点内，整个点云模型分成很多块，记为Surfacei。

对于每个 Surfacei内的点云再进行递归深度为2的八叉树切分，找出所有非空子节点中离Surfacei最小包围盒中心最近的子节点，从子节点任意取一个点记为o，并找出离o点最近的10个点，记为qi，利用这10个点对该单元点云拟合平面进行粗估计。求矩阵：

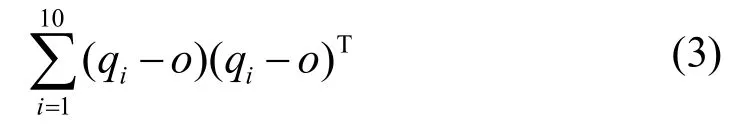
最小特征值的特征向量，记为v，v=(xv, yv, zv)做为拟合粗平图的法向量，点o为拟合平面上一点，如图8所示。对xv，yv，zv的绝对值进行升幂排列。假设 Surfacei内点云数量为num，法向量v的升幂排列为yv，xv，zv，取。首先全部 num个点云按照v中绝对值最小的方向分量yv升幂排列，沿y坐标从小到大每L×m个点云一组，接着对每一组点云按照v中绝对值第二小的方向分量xv升幂排列，沿着x坐标从小到大每m个点云一组，对于最后的一组点云数量可能小于m，如果小于合并到前一组，否则单独一组，至此点云切分完毕。

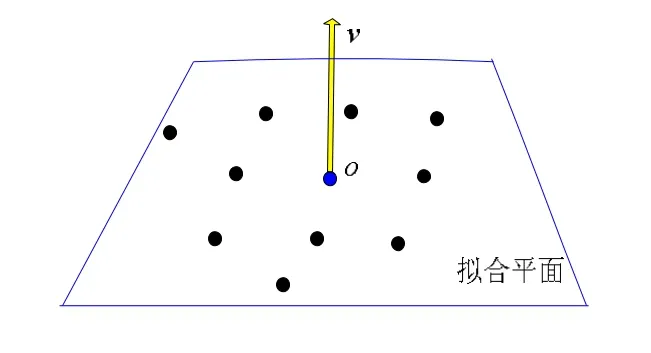
图8　点云粗拟合平面

2.4最小生成树生成与压缩

在点云模型切分之后，首先需要对每个单元内点云进行预测编码，然后进行编码压缩处理。文献[7]首次将最小生成树应用点云预测压缩中，取得明显压缩效果。本文采用最小生成树进行预测，具体以每个单元内点云之间的曼哈顿距离作为权值，采用Prim算法[18]生成单元最小生成树。

本文Prim算法流程如下：

设G=(V, E)，其最小生成树S=(U, TE)。

(1) U，TE为空，从V中取出一点o加入U。

(2) 查找V和U中权值最小的两点记为x和y，从V取出x加入U，边(x, y)加入TE中。

(3) 重复步骤(2)直到V为空。

对于点云数据的预测压缩需要最小生成树的信息，在对点云数据解压时，也需要用最小生成树的信息对其进行解码，因此，可单独对最小生成树编码压缩，记录父节点的子节点个数。如图9所示，1号节点有2个子节点2和3，2号节点有1个子节点 4，采用算术编码[19]依次记录父节点的子结点个数。2.5顶点数据压缩

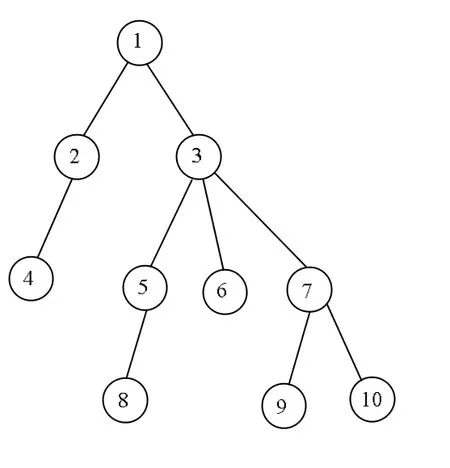
图9　最小生成树示意图

点云顶点数据首先经 FtoI规则由浮点数类型转换成整数类型，顶点数据压缩是对于整型数据的压缩，具体步骤分3步：

(1) 对于每个单元块内的点云根据其最小生成树求对应父子节点的差值，对整型的差值进行编码压缩，编码顺序为最小生成树宽度优先。树形结构如图9所示，编码顺序：首先编码1号节点的原值，其次2、3号节点与1号节点的差值。然后4号节点与2号节点的差值，5、6、7号与3号节点的差值。最后8号节点与5号节点的差值，9、10号节点与7号节点的差值。

(2) 由于三维点云数存在3个坐标方向，对x、y、z 3个坐标数据分别编码压缩。如果直接对 32位整数差值进行编码压缩，会影响压缩效果，为了提高压缩率，减少每一个差值所占用的Bit位，在每一个单元内，求每个方向绝对值最大的差值Max，绝对值部分采用n位Bit存储，其中n满足以下条件：

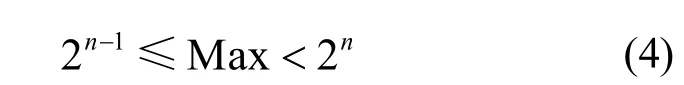
而符号部分采用1位Bit存储。把整型差值分成两部分编码，符号一部分，其绝对值一部分，整个差值所占Bit位为n+1。

(3) 为了达到更好地压缩效果，对差值部分进行算术编码压缩。由于符号位部分的值0和1分布随机，采用算术编码没有明显的压缩效果，而且增加了时间开销，因此对符号部分直接存储。而绝对值部分，其值小于Max，统一采用n位Bit记录，其中一些值远小于Max，高位中0的出现概率大于1的出现概率，因此采用算术编码压缩会达到较好地压缩效果。由于大多数计算机最多支持的 80位或差不多的浮点数，必须在每次完成有限个符号后重新开始，采用增量转换方法来代替浮点数，形成一个较大的单数取代对应的浮点数，这个单数的位数可以很大，从而解决了浮点数位数有限的不足。

3　实验结果与分析

在CPU2.2 GHz，2 G内存，W indows 7系统的电脑上实现本文算法，点云模型采用Stanford大学标准的点云模型。

对于点云模型切分的大小决定了点云数据压缩时间和压缩率的大小，单元切分的过大，导致最小生成树的时间开销过大，时间效率低下，而单元切分的过小，会导致编码不连续性，使算法压缩率过低。对于单元点数的选择，通过对Bunny模型进行实验分析，其含40 257个点云数据。实验数据见表1，图10是压缩率和压缩时间对应趋势的曲线图，由图 10可看出，随着每单元点云数量增加，压缩时间相应增加，而压缩率先提高再降低。综合数据分析，为达到压缩时间和压缩率的最优平衡，选点云数量为70的压缩块。压缩时间以ms为单位，压缩率以bpp(bits per point)为单位，即每个点数据所占二进制位数。

表2是3个标准点云模型的最大点距误差比和平均点距误差比，其中点距误差比在10-4以下，表明有损压缩后的点云模型与原始点云模型几乎一致。

表3和图11给出本文算法(简称New)和传统7zip以及文献[8]算法(简称Wang)压缩率的比较，表明本文在压缩率方面有良好的表现。同时本文算法在压缩速度方面也有不俗的表现，平均压缩速度约为200 k点/s，而7zip压缩速度约为1.5 M/s，转换成统一速度单位点/s，对于二进制文件格式点云，压缩速度约为130 k点/s，对于文本文件格式点云，压缩速度约为 45 k点/s，Wang算法压缩率约为25 k点/s。同时本文解压缩不需要压缩时的前期处理，在时间上明显小于压缩时间，约为其八分之一，解压缩平均速度为1 600 k点/s。

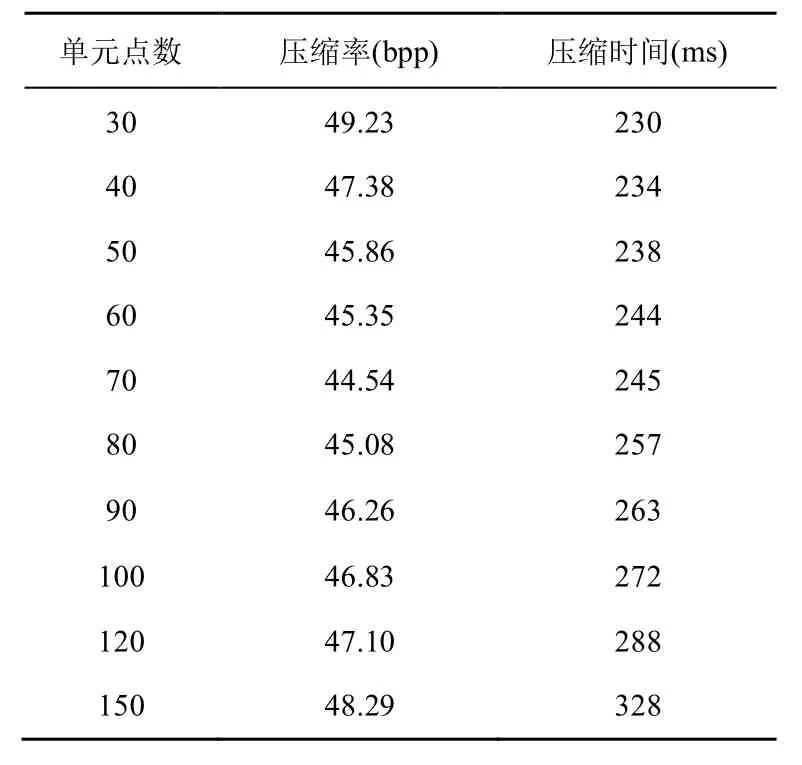
表1　不同点云数量对算法压缩率和压缩时间的影响

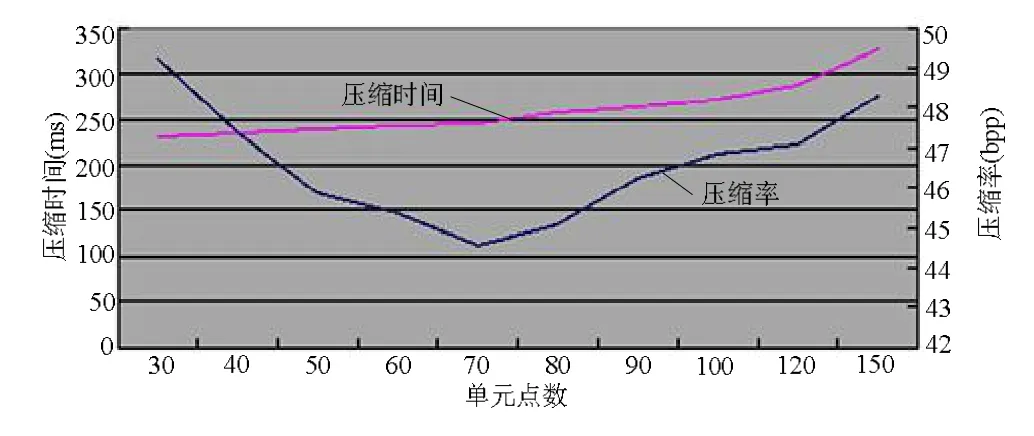
图10　本文方法的压缩率和压缩时间随点云数量变化曲线图

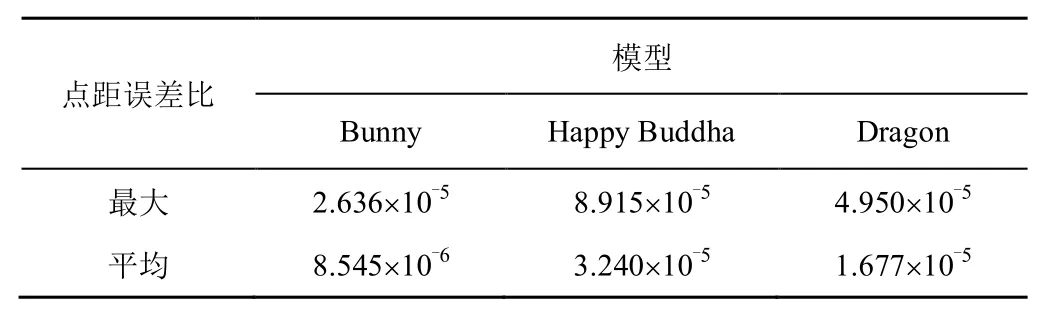
表2　不同点云模型的点距误差比

表3　3种算法压缩率的对比

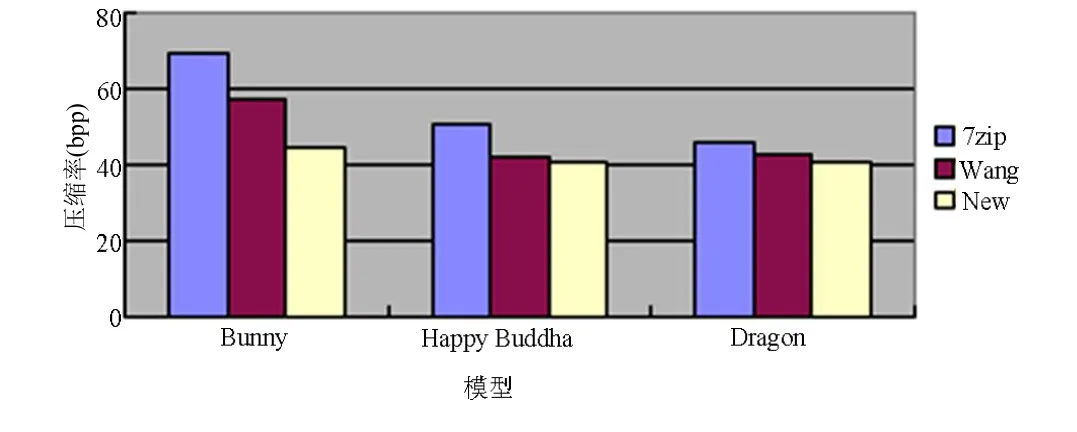
图11　3种算法压缩率的比较图

4　结论与展望

本文提出了一种基于 FtoI规则的点云快速有损压缩算法，该算法对部分点云的精度损失极其微小，不会影响整个三维点云模型的整体质量。FtoI规则首先将浮点数统一精度，然后转换成整数，可以有效地减少了计算复杂度和内存开销。实验结果表明该算法有较好地压缩速度和压缩率。

浮点数表示的精度很高，但在工程实践中有时候不需要很高的精度。本文的点云快速有损压缩算法可以实现不同精度的压缩，在点距误差比很小时，可以适当降低精度，从而达到更高的压缩率。在今后研究中可以结合点云精简技术，根据需求对整个模型的点云数量进行处理，尽量减少压缩时间和内存开销。

[1] Levoy M, Whitted T. The use of points as a display primitive [R]. Chapel Hill: University of North Carolina, 1985.

[2] Kobbelt L, Botsch M. A survey of point-based techniques in computer graphics [J]. Computer & Graphics, 2004, 28(6): 801-814.

[3] Gross M, Pfister H. Point-based graphics [M]. San Francisco: Morgan Kaufman Publisher, 2007.

[4] 王鹏杰, 潘志庚, 刘勇奎. 基于点的三维模型压缩技术研究进展[J]. 计算机辅助设计与图形学学报, 2009, 21(10): 1359-1367.

[5] Zhang C, Florêncio D, Loop C. Point cloud attribute compression with graph transform [C]//Image Processing (ICIP), 2014 IEEE International Conference on. New York: IEEE Press, 2014: 2066-2070.

[6] 何辰. 基于形状分析的三维点云模型压缩[D]. 济南:山东大学, 2014.

[7] Gumhold S, Karni Z, Isenburg M, et al. Predictive point cloud compression [C]//Proceedings of SIGGRAPH Sketches. New York: ACM Press, 2005: 137.

[8] 王鹏杰, 潘志庚, 徐明亮, 等. 基于局部最小生成树的点模型快速无损压缩算法[J]. 计算机研究与发展, 2011, 48(7): 1263-1268.

[9] Morell V, Orts S, Cazorla M, et al. Geometric 3D point cloud compression [J]. Pattern Recognition Letters, 2014, 50: 55-62.

[10] 范然, 金小刚. 大规模点云选择及精简[J]. 图学学报, 2013, 34(3): 12-19.

[11] Chen D, Chiang Y J, Memon N. Lossless compression of point-based 3D models [J]. Proceedings of Pacific Graphics, 2005: 124-126.

[12] Isenburg M, Lindstrom P, Snoeyink J. Lossless compression of floating-point geometry [J]. Journal of Computer-Aided Design, 2005, 37(8): 869-877.

[13] IEEE 754-1985, Standard for binary floating point arithmetic [S]. New York: The Institute of Electrical and Electronic Engineers Inc, 1985.

[14] Fabio R. From point cloud to surface: the modeling and visualization problem [J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2003, 34(5): W 10.

[15] Hunter G M. Efficient computation and data structures for graphics [D]. Princeton: Department of Electrical Engineering and Computer Science, Princeton University, 1978.

[16] Elserberg J, Borrmann D, Nuchter A. One billion points in the cloud-an octree for efficient processing of 3D laser scans [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 76: 76-88.

[17] Schnabel R, Klein R. Octree-based point-cloud compression [C]//SPBG’06 Proceeding of the 3rd Eurographics. New York: IEEE Press, 2006: 111-120.

[18] Cormen H, Leiserson E. Introduction to algorithms [M]. 3rd ed. Cambridge: The M IT Press, 2009: 624-643.

[19] Witten I H, Neal R M, Cleary J G. Arithmetic coding for data compression [J]. Communications of the ACM, 1987, 30(6): 520-540.

A Fast and Lossy Com pression A lgorithm for Point-Cloud Models Based on Data Type Conversion

Lv Shuai,Da Feipeng,Huang Yuan

(School of Automation, Southeast University, Nanjing Jiangsu 210096, China)

In order to solve computer storage and transmission problem due to massive 3D point cloud, a fast and lossy compression algorithm for point-cloud models based on data type conversion is proposed. Firstly, a data type conversion rule-FtoI rule is designed. According to the FtoI rule, float-point type point cloud is converted to integer type point cloud, then the integer type point-based surface is split into many sized surface patches, the points of every patches construct a minimum spanning tree, which is encoded in breadth first order. Besides we encode the difference between father node and son node according to the minimum spanning tree, the difference is split into two parts, one is sign, another is absolute value, which is encoded by arithmetic coding. Experiments show that this compression algorithm has a nice compression speed and compression ratio without losing the quality of point-cloud model.

3D point cloud; lossy compression; float; the m inimum spanning tree; arithmetic coding

TP 391.41

10.11996/JG.j.2095-302X.2016020199

A

2095-302X(2016)02-0199-07

2015-09-24；定稿日期：2015-10-20

国家自然科学基金项目(61405034, 51175081, 51475092)；教育部博士点基金项目(20130092110027)

律帅(1989–)，男，山东济宁人，硕士研究生。主要研究方向为三维数据压缩。E-mail：lssoutheast@163.com

达飞鹏(1968–)，男，江苏南通人，教授，博士，博士生导师。主要研究方向为三维精密测量研究与应用。E-mail：dafp@seu.edu.cn