基于马尔可夫模型的路网养护管理排序问题研究

白国鹏，李换平，李笑宇

（1.天津市市政工程设计研究院，天津 300051；2.哈尔滨工业大学交通科学与工程学院，黑龙江哈尔滨 150090）

基于马尔可夫模型的路网养护管理排序问题研究

白国鹏1，李换平2，李笑宇1

（1.天津市市政工程设计研究院，天津 300051；2.哈尔滨工业大学交通科学与工程学院，黑龙江哈尔滨 150090）

对马尔可夫排序模型进行研究，分析了该模型在路网养护管理中的适用性；建立了路网多因素排序模型，通过在实例分析中绘制马尔可夫图，阐明了马尔可夫排序模型的应用原理，并利用MATLAB程序对模型进行了求解，为解决路网养护规划中的养护路段排序问题提供依据。

工程管理；路网养护管理；马尔可夫；排序模型

随着中国公路网建设进入尾声，路网的养护资金投入、养护资金分配等养护投资规划问题日益明显，主要表现为严格按照规范要求进行养护所需资金不足、具体路段的养护对策难以从长远意义角度出发进行选取、资金的利用效率低等。这些问题的存在严重影响了路网路况，养护资金投入不合理使得路网错过了最佳养护时机，养护对策选取不合理则导致路况过早过快恶化。同时由于不同气候地区路网的主要病害与破坏形式均不相同，养护规划的影响因素众多。人为地对每个路段进行排序来确定养护优先级是不客观的，如何科学、客观地对路网道路进行养护排序显得尤为重要。

马尔可夫排序模型的核心思想在于投票，而排序就是所有投票人的选票结果。不同的是，投票人不是每一位专家，而是马尔可夫排序模型里客观存在的随机游走的评分人（称其为墙头草评分人）。该文拟利用马尔可夫排序模型对路网道路进行多因素排序，解决路网养护规划中的排序问题。

1 马尔可夫排序模型适用性分析

马尔可夫排序模型是多因素排序模型，其核心思想充分体现了模型的客观性，尽量减少了主观排序的可能。该模型为其客观性所付出的代价是计算量增大，但现在计算机性能的不断提高使将马尔可夫排序模型用于处理大型路网排序问题成为可能。

马尔可夫排序模型的原理是：系统中客观存在一个墙头草随机游走的评分人，根据墙头草在马尔可夫图上随机游走时在每个节点上所消耗的时间比例获得评分排名即马尔可夫评分向量r，根据该向量进行排序。将公路网内的每个路段进行养护优先排序的过程比拟为马尔可夫排序的投票过程，根据每个需要养护路段的自由属性来确定每个养护路段的养护优先级。

2 建立马尔可夫路网养护排序模型

根据某项指标（如交通量、指标值）的分差，建立马尔可夫排序模型随机矩阵V，称其为马氏排序模型原始矩阵；通过对V进行归一化处理、全胜队伍处理，得到具有稳态向量的随机矩阵Si；利用每个指标的Si计算得到最终随机矩阵S；计算S的稳态向量（主特征向量），得到马尔可夫排序模型评分向量r即排序结果。

为了更清晰地表达模型建立的过程，选择交通量（年平均日交通量AADT）和路况指标（如路面状况指数PCⅠ）双变量进行阐述。将交通量作为排序的因素之一，可优先对交通量大的路段进行养护。某路段的交通量越大，在路网中发挥的作用就越大。单纯考虑交通量因素也存在缺点：路段的交通量小，路况将持续下降，交通量也将随之更小，下拨的资金就更少，路况将更差，形成恶性循环。决策者不希望看到这种情况，所以考虑添加路况指标作为另一变量来平衡这种缺点，路况差的路段将获得更为合理的分配资金的机会，整体上改进了模型。

马尔可夫排序模型不局限于双变量排序，可根据决策者的需求采取多变量排序的方式。

双变量排序中的每个变量都存在一个权重α1、α2，若它们同等重要，则α1=α2=0.5，只要保证α1+ α2=1且αi≥0即可。基于交通量（AADT）和路况指标（PCⅠ）双变量模型的建立步骤如下：

（1）建立马尔可夫原始矩阵：

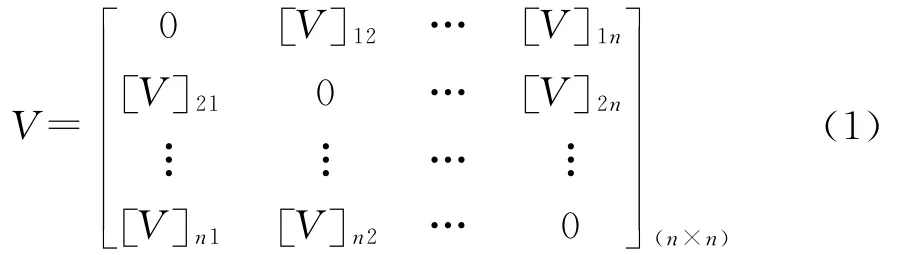
式中：［V］ij表示V中第i行第j列的数值；n为路段总数。

式中：VAADT为按交通量统计数据建立的马氏原始矩阵；VZB为按道路性能指标均值统计数据建立的马氏原始矩阵；ZB为道路性能指标值与满分之差。

（2）根据马尔可夫原始矩阵V按式（4）计算马尔可夫随机矩阵S。SAADT、SZB分别对应VAADT、VZB，分别根据VAADT、VZB计算得到。然后根据各因素权重按式（6）计算马尔可夫随机矩阵SEnd。

式中：［S］ij代表矩阵S中第i行第j列的值。

式中：SEnd为全部S构建的最终随机矩阵，本例中由SAADT和SZB构建；αi为统计数据对应权重。

（3）为了保证SEnd具有不可约性，使其拥有稳态向量，按式（7）对SEnd进行处理。¯S不可约，保证了其稳态向量存在且唯一。¯S内的数值依赖于标量β的选择，通常β越大，模型越符合原始数据。这里采用全胜队伍均等对所有队伍投票的算法保证¯S矩阵的不可约性，并取β=1。

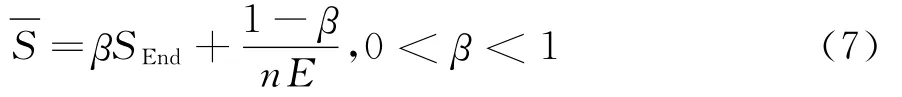
（4）计算每个路段的权值分量。利用式（8）、式（9）计算路网权值向量r，得到路网中所有路段的排序。由于计算得到的每个路段的权值分量均小于1（［r］i＜1），对于一些有养护硬性要求的路段，只要将其评分值设置为1，即可得到路网所有路段的排序方案。

式中：λ为¯S转置矩阵的特征值；Ⅰ为n阶次对角阵，为主对角线全为1的矩阵；r为马尔可夫评分向量，为¯S转置的稳态向量（即主特征向量）。

3 实例分析

下面通过一个实例对上述模型进行说明并求解。随机取江苏南京G104国道K1132—K1136路段5个上行路段进行养护优先排序，其2013年路面状况指数PCⅠ、路面行驶质量指数RQⅠ、路面车辙深度指数RDⅠ、路面抗滑性能指数SRⅠ等指标值见表1。

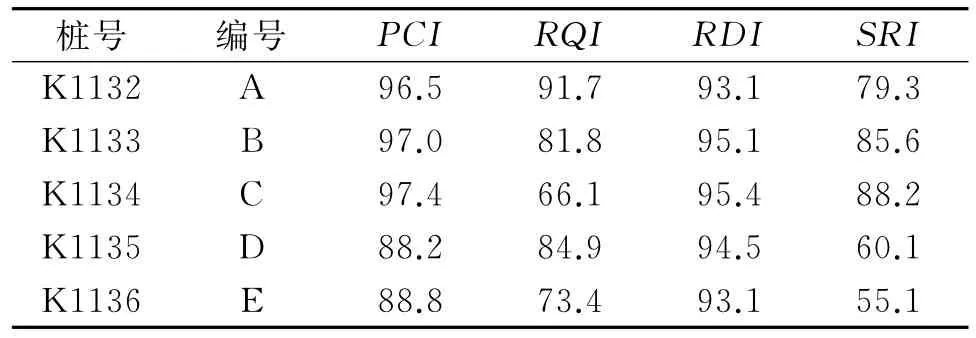
表1　5个路段的路况指标值

从表1来看，RQⅠ差异较大。下面第1～3步以RQⅠ为例进行计算，其他指标类似。RQⅠ指标值与满分之差见表2。

表2　5个路段的RQⅠ指标值

（1）计算马尔可夫原始矩阵（投票矩阵）：

（3）为了保证得到的马尔可夫随机矩阵S具有稳态评分向量，采用全胜队伍均等对所有队伍投票的算法进行计算，得到S。绘制马尔可夫排序图（见图1），用以表示马尔可夫模型的物理意义即墙头草评分人在每一个节点上所消耗的时间，从而获得评分排名。

图1　模型评分人在马尔可夫图上进行一次随机游走

（4）计算SEnd。本例采用PCⅠ、RQⅠ、RDⅠ、SRⅠ4个指标进行排序，采用JTG H20-2007《公路技术状况评定标准》中计算PQⅠ时的各指标权重，对于沥青路面，道路等级为一级公路的权重值分别为0.35、0.4、0.15、0.1。按式（6）计算，得到最终随机矩阵：

（5）利用MATLAB计算ST的稳态向量即主特征向量，程序如下：1）对S赋值，S=［0.03，0.10，0.20，0.30，0.37；0.09，0，0.26，0.23，0.42；0.17，0.10，0.08，0.31，0.34；0.15，0.11，0.30，0.07，0.38；0.05，0.05，0.45，0.40，0.05］；2）利用eig函数计算ST的所有特征值及特征向量，［X，Z］=eig（S′）；3）取特征值的模，M=abs（X）；4）计算主特征向量并归一，T=M（：，1）/sum（M（：，1））。计算结果见表3。

表3　马尔可夫排序模型5个路段的排序结果

4 结语

该文旨在研究一种客观有效的多因素排序方法，用以解决路网养护中对养护道路优先选取问题。利用马尔可夫排序模型建立路网养护排序模型，为解决路网养护规划中的养护优先排序问题提供了一种新方法。

［1］ Sergey B，Lawrence P，Motwami R，et al.The page rankcitation ranking：bringing order to the web［R］. Technical Report，1999.

［2］ Luke I.Ranking NCAAsports teams with linear algebra［D］.College of Charleston，2007.

［3］ Anjela Y G.Rankingtheory with application to popularsports［D］.North Carolina State University，2008.

［4］ JTG H20-2007，公路技术状况评定标准［S］.

［5］ 刘燕，刘剑峰，王宁宁.山区农村公路区域路网养护管理决策研究［J］.公路与汽运，2008（4）.

［6］ 喻翔.高速公路路面养护管理系统决策优化的研究［D］.成都：西南交通大学，2005.

U418.2

A

1671-2668（2016）05-0234-03

2016-05-23