一种基于关系数据库管理系统的图计算平台

蒋奎,陈亮

(1.河北轨道运输职业技术学院,石家庄050021; 2.微软亚洲研究院,北京100080)

一种基于关系数据库管理系统的图计算平台

蒋奎1,陈亮2

(1.河北轨道运输职业技术学院,石家庄050021; 2.微软亚洲研究院,北京100080)

本文提出了一种新的基于关系数据库管理系统(Relational Database Management System,RDBMS)(本文简称关系数据库)的图计算平台.该平台将图数据以原生的形式在关系数据库的表格中存储,从而在数据表达上和原生图计算平台达到了一致.该平台将图计算逻辑完整准确地表达为SQL(Structured Query Language)查询语句.关系数据库执行SQL查询语句,从而完成图计算,并将结果返回.实验结果表明,该新的平台有效地利用了关系数据库成熟的查询优化技术,在很多方面优于现有的原生数据平台;而目前的性能局限,也会随着未来关系数据库的不断演化和迭代,得到有效的解决.

关系数据库管理系统;图计算;原生图计算平台

0 引言

图数据在今天的企业环境中无处不在,它的大量出现使得越来越多的应用需要高效地分析、处理、计算图数据,进而对图计算平台产生了大量的需求.虽然今天关系数据库(RDBMS)在企业中是最为重要的数据平台,但它的成功常常被看作仅仅局限于表格数据,而在图计算领域面临着诸多困难.事实上,在最近的NoSQL(Not Only SQL)趋势中,大量的原生图计算平台纷纷涌现[1-3],其中的绝大部分放弃了关系数据库,从而完全重新设计、实现针对图数据的存储和查询引擎.

原生图计算平台和关系数据最明显的区别体现在两方面:数据存储和计算语言.和关系数据库的表格相比,原生图计算平台中最为自然的表达图的数据结构为邻接表(Adjacency List).邻接表为一个链表,链表中的每一个元素代表了一条指向邻居节点的边.物理表达上,链表中的每个元素为邻居节点的ID(Identification).通过链表中的ID可以在底层存储中定位每个邻居节点.如果每条边上还附带有属性,则链表中的元素从节点ID变为一个元组(Tuple),该元祖不仅包含邻居节点的ID,还包含边上的属性.

在原生图计算平台中,广泛采用的编程模型为BSP(Bulk Synchronous Parallel)模型[4]. BSP模型最早在并行计算中被提出,因为近些年在Google的Pregel图计算平台上被采用而广为人知[5].BSP模型将图中的每一个节点定义为一个计算单元,每个计算单元维护自己的状态,并不断从它的邻居节点接收邻居的状态,用它们来更新自己的状态.该更新过程一直持续,直到所有节点的状态都已经收敛,或者某个定义的参数满足某些条件.正像Google在Pregel中展示的那样,大多数图计算算法都可以通过该模型来表达,比如最短路径、PageRank算法以及最小生成树(Minimal Spanning Tree).

基于邻接表的数据表达以及BSP的编程模型,看起来和传统关系数据库的表格以及SQL语句有着巨大差距.长久以来,基于关系数据库的图计算研究一直十分有限.如何利用关系数据库成熟、高效的查询优化技术来支持图计算,不仅有学术价值,还有着深远的实际价值,能使数百万关系数据库的用户更为方B地利用现有平台满足新的计算需求.

本文提出了一种新的基于关系数据库(RDBMS)的计算平台.该平台采用了和原生图计算平台相同的数据结构来表示图数据:邻接表.在该数据表达之上,平台利用SQL查询语句表达BSP程序逻辑,并将该SQL语句在底层的关系数据库运行.SQL查询语句包含了迭代逻辑,在每一轮迭代中不断更新节点上的状态,直到收敛.同时,图算法的优化可以同通过SQL语句准确清晰地表达出来,极大地提高了图计算的性能.

在本文中,平台的实现以SQL Server数据库为基础.SQL Server数据库是主流关系数据库之一.本文中介绍的用于实现邻接表和BSP编程的技术,在其他关系数据库中也可以找到相应的对应.

1 图在关系数据库中的表达和解析

在本节中,我们分别讨论邻接表以及图数据在关系数据库中的表示和操作,这是图计算的基础.

1.1 图的表达:邻接表

图数据由节点和边组成.节点和边上可以附带额外的属性.一个节点上的所有出边(Outgoing Edges)组成了一个邻接表(Adjacency List),表中的每一个元素代表了一条指向邻居节点的边.在物理表达上,邻接表中的每个元素为一个元组(Tuple),它包含了这条边所指向的邻居节点的ID,以及该边上的属性.类似,一个节点上的所有入边(Incoming Edges),组成了另外一个邻接表,其中的每一个元祖代表了一条指向节点自己的边.在图的操作中,给定一个节点,访问该节点的邻居十分方B:通过遍历邻接表,可以方B地知道每个邻居节点的ID,通过ID也就可以进一步定位到邻居节点.

尽管邻接表十分方B图的遍历,但在关系数据库中表达邻接表却十分困难.其根本原因在于,关系数据库中表格的一列无法存储一个链表;一个多值集合只能存到额外的表格中,并通过主键(Primary Key)和外键(Foreign Key)将两张表格联系起来,进而丧失了邻接表的方B.在系统实现中,这个困难直接导致了众多系统开发人员放弃了关系数据库作为图数据的存储引擎,进而设计原生图存储.

本文提出了一种新的在关系数据库中表达邻接表的方式,克服了上述提到的困难.其基本思想如下:尽管邻接表无法直接存储于表格的一列中,但它可以被序列化为二进制字符串.现有的关系数据库都对变长二进制字符串有着很好的支持,会自动根据字符串的长短分配地址空间.因此通过将链表序列化,就能把邻接表存放于表格的一列中,达到和原生图存储相同的数据表达.

给定邻接表的表达,图数据可以方B地存储在关系数据库的表格中:每一个节点映射到表的一行;节点的每一个属性,映射到表格的一列;节点出边的邻接表和入边的邻接表分别映射到两个特殊的二进制字符串列.图1给出了一个社交网络图在SQL Server数据库的存储样例.在该表格中,第一列存储节点ID;第二列存储节点上的属性,即每位用户的姓名;第三列存储出边的邻接表.在SQL Server数据库中,邻接表以二进制字符串存储.

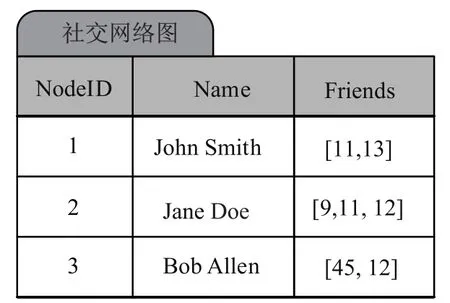
图1 社交网络图在SQL Server数据库中存储样例Fig.1An example of a social network graph in SQL Server

1.2 图的解析

把邻接表以二进制字符串存储在关系表格中,关系数据库的查询引擎无法知晓该字符串的语义,也就无法用传统的SQL语句来实现图的遍历.本节介绍如何通过SQL Server数据库的扩展技术,将邻接表解析为SQL Server数据库可见的数据,进而用SQL语句实现从一个节点游走到邻居节点.该技术对其他关系数据库同样适用.

图的单步游走包含了3个基本步骤:①将节点从底层存储中取出;②遍历该节点上的邻接表;③对于每个邻居节点指针(即邻居节点ID),定位到相应的节点.第一步操作对应为SQL查询语句中的一个或多个查询条件.第二步操作是一个遍历操作,因为关系数据库只能对表格进行遍历,因此,二进制表达的邻接表必须首先转化为表格.在SQL Server数据库中,这样的转化由TVF(Table-Valued Function)函数来实现.TVF函数是一个用户自定义函数,由C#实现,它传入一个标量数据,返回的则是表格数据.TVF函数必须实现3个标准接口Reset()、Current以及MoveNext(),使得SQL Server数据库能不断调用这些接口,将标量数据转化为表格数据.TVF函数的接口和定义参见图2.

在图计算平台中,我们把解析邻接表的TVF函数称为Transpose.Transpose传入的是二进制表达的邻接表.通过TVF函数中MoveNext()的实现,Transpose完成对二进制字符串的解析.通过Current接口,它不断地将当前解析出的边返回给SQL Server数据库引擎.SQL Server数据库将新解析出的边插入到临时表格中,并通过该临时表格将邻居节点的ID最终传递给下一级的SQL语句.二进制表示的邻接表的完整解析过程参见图3.在图中,邻接表被解析到一个临时表中.临时表包含两列,第二列Sink包含了每个起始节点的邻居指针.

图2 TVF函数的接口与定义Fig.2Interfaces and definition of a table-valued function(TVF)

图3 二进制邻接表的解析Fig.3Decoding of serialized adjacency lists

在邻接表被解析成临时表格之后,单步游走的最后一步通过Join操作完成,即将临时表的每一个邻居指针(即邻居ID)和邻居节点关联起来.完整的查询语句如下所示.

SELECT friend.NodeID,friend.Name

FROM SocialTable AS user CROSS APPLY Transpose(user.Friends)AS E

JOIN SocialTable AS friend on E.Sink=friend.NodeID

WHERE user.Name=‘John Smith'

2 图计算编程和优化

2.1 BSP实现简述

BSP(Bulk Synchronous Parallel)为现有图计算平台的主要编程模型,它给每个节点定义一个状态,每个节点根据邻居的状态不断更新自己的状态,直到状态收敛.BSP模型又分为“同步BSP”和“异步BSP”.同步BSP规定每个节点第k轮的状态由其所有邻居的k一1轮状态决定.因此,只有当所有节点的第k一1轮状态计算完毕,节点的k轮状态才能开始计算,即存在一个全局的分界点将第k轮计算和第k一1轮计算明确地分隔开.相比而言,异步BSP则放松了每一轮更新对邻居节点状态的要求,节点的第k轮状态可以由其邻居节点的k一l轮状态决定,l≥1.由此,异步BSP并不需要全局的分界点将所有节点的k一1轮计算和k轮计算分隔开来.在任意时刻,有些节点的状态处于第k轮,而有些节点的状态可能已经是第k+l轮,l＞1.同步BSP与异步BSP比较起来,逻辑清晰,实现简单.因此也成为图计算平台主要的编程模型.在本文的讨论中,我们主要关注同步BSP.

同步BSP可以在本文提出的图计算平台上通过SQL语句方B地表达和实现.每个节点的状态映射到表格中的一列.在每一轮迭代中,每个节点需要从邻居接受其上一轮的状态.这个操作通过解析邻接表以及Join操作将每个节点和邻居节点关联起来.接着,每个节点的状态更新表达为基于该节点的聚合函数(Aggregation Function).最后通过SQL提供的循环语句控制迭代.因为在关系数据库中,两次循环的执行不会重叠,两次循环之间存在着一个全局分界点.由此,所有节点的同步也得到天然的保障.

BSP编程模型及其对应的SQL语句有很强的表达力,能表达多种图算法,比如最短路径和最小生成树.因为每个算法细节不同,实现起来也各不一样,在本文中无法穷尽.在下面的讨论中,我们着重关注一个很有代表性的实例:PageRank算法的实现和优化.其他图算法可以类似实现.

2.2 PageRank算法实现

PageRank算法是链接分析里很重要的一个算法.它通过迭代运算给每个节点赋予一个分数.分数越高的节点,重要性越高.在迭代初始状态,所有节点被赋予相同的分数.以上面提到的社交网络为例,我们将图1中的表格扩展一列Score,用来存储每个节点的分数.在每一轮迭代中,每个节点将自己的分数和指向自己的邻居的分数加权叠加,得到自己新的分数.当节点的分数更新后不再改变,则该节点收敛;当所有节点收敛后,迭代运算也就终止.我们将图1中的表格再扩展一列Converge来表示每个节点在哪一轮收敛,Converge=0表示该节点还未收敛.

图4展示了PageRank实现的代码样例.在循环内部中,SQL语句通过Transpose函数解析邻接表,并通过Join将每条边的起点和终点关联起来.在此基础之上,SQL通过GROUP BY语句和聚合函数计算每个节点新的PageRank分数.该聚合函数是一个简单的求和函数,将每个节点邻居的分数加权求和.在代码中,BinaryCount是另一个自定义函数,用来计算给定邻接表的长度.

2.3 PageRank算法优化

图4给出的PageRank的代码是在SQL Server数据库上最朴素的实现.针对具体的图算法特性,经常会有算法级别的优化.这类优化不依赖于底层系统,和具体算法紧密相关,因此很难抽象为统一的优化策略而在系统中实现.一个好的图计算平台应该提供有足够表达力的语言,使得算法设计和实现者能在该平台上将这些优化准确、简洁地实现出来.本文提出的计算平台,利用SQL语句表达算法逻辑,能很好地满足这一需求.本小节以PageRank为例,展示如何利用SQL语句来实现PageRank算法的优化.

PageRank的计算是一个非常耗时的过程,很重要的一个原因就是每一轮迭代需要对全图进行遍历.同时,只要有任何节点没有收敛,迭代就要一直进行下去.之前的研究者观察到一个很重要的现象,可以用来极大的降低计算复杂度[6]:在PageRank分数的计算过程中,只有少数分数很高的节点迟迟不能收敛;大多数分数较低的节点在开始几轮迭代后很快就收敛了,在迭代过程中,已经收敛的节点就不用再继续计算了;同时,收敛节点对于未收敛节点分数的贡献也就固定不变了.如果在每轮迭代中,重用收敛节点的分数以及它们对其他节点的贡献,那每一轮的迭代就可以避免重复计算,从而大大降低计算复杂度.下面我们将该优化思想以数学公式严格地表达出来.

图4 PageRank实现代码样例Fig.4PageRank implementation using SQL

PageRank的计算可以用迭代公式

描述,其中,X是一个向量,每一维代表了一个节点的PageRank分数,Xk代表了第k轮迭代后所有节点的分数,A为图的邻接矩阵.

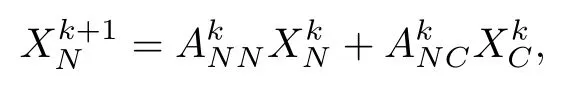
我们将上述的所有优化移植到图4的SQL语句中,就得到了优化后的PageRank算法实现,如图5所示.图5和图4代码的不同之处在图5中通过加黑高亮出来.在内部查询语句里,加入了条件

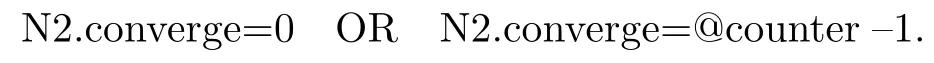
该条件用在每一轮选出未收敛节点或者有最新收敛的节点.每一轮查询语句计算两个数值: scoren和deltac.前者对应,计算了所有未收敛节点之间互相的分数贡献;后者对应在每一轮的增量.

图5 PageRank优化后的PageRank实现Fig.5An optimized implementation of PageRank in SQL

3 实验结果

本节对本文提出的基于关系数据库的图计算平台进行实验评估.底层的关系数据库为SQL Server数据库.我们选取GraphLab作为对比系统[3].GraphLab是一个用C++编写的并行图计算平台,它提供了BSP类型的编程接口,使得开发者能够方B地在上面实现图算法.GraphLab的系统以迭代式图算法为主要设计目标,其性能也以迭代式算法而著称.在数据存储上,GraphLab将节点以对象的形式存储在内存中.在默认模式下,GraphLab仅仅维护内存对象,而不会将这些对象同步到磁盘上.因为完全避免了磁盘访问,这种模式会给GraphLab带来极大的性能优势.但另一方面,这种模式对于关系数据库并不公平.在关系数据库里,任何更新都有事务(Transaction)保障,所有操作的结果都时时同步到磁盘上,以防硬件出错和机器重启以后结果丢失.没有了同步机制,如果运算因为各种原因中断,GraphLab将会丢失所有中间结果,而不得不从头开始.因此,GraphLab也提供了同步机制,允许使用者指定一定的间隔将所有节点同步到磁盘上.在实验中,我们分别考虑了下面两种模式下的性能.

我们选取了两组数据来评估PageRank算法在基于SQL Server数据库的图平台和GraphLab上的运行效率.两组数据都来自斯坦福大学发布的万维网超链接图,两组数据的大小如表1所示.

表1 实验数据集Tab.1Experiment data sets

我们首先测量了GraphLab在有同步机制下和SQL Server数据库的性能比较.GraphLab在PageRank每轮迭代完后,将当前图的状态同步到磁盘上.在每组实验中,我们分别测量了无优化的PageRank算法和优化后的PageRank的算法.实验结果如图6所示.可以看到,在这组实验中,基于SQL Server数据库的PageRank性能远远好于GraphLab.当PageRank算法没有任何优化时,两个系统迭代次数相同.在每轮迭代中,因为所有节点的分数都要更新一遍,和磁盘之间同步的数据量也相同.但是基于SQL Server数据库的图计算的性能仍然大大高于GraphLab.我们将这样的性能差距归咎于关系数据库长期以来的对磁盘读写的优化.相比较而言,GraphLab开发时间较短,在磁盘读写上还有很多设计和实现需要优化.对于优化后的PageRank算法,SQL Server数据库的性能优势更加明显;性能提升在20倍左右.这是因为,优化后的PageRank算法每一轮迭代只会更新还未收敛的节点.在开始几轮迭代后,需要更新的节点数量锐减,进而磁盘读写也会大大降低.而GraphLab并未实现增量式同步机制.所以每一轮迭代后,所有节点都要被写回磁盘,即使它的状态没有任何更新.GraphLab在这种模式下,几乎没有享受到PageRank算法优化所带来的好处.

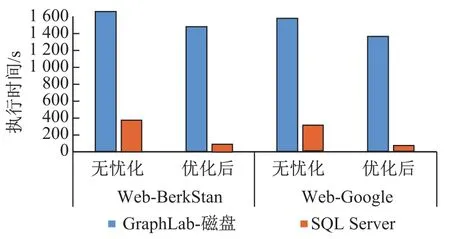
图6 GraphLab磁盘和SQL Server数据库PageRank性能比较Fig.6Performance comparison between GraphLab-disk and SQL Server

在第二组比较实验中,我们测量GraphLab在没有同步机制下的性能.实验结果如图7所示.可以看到,当GraphLab没有任何磁盘读写时,其性能大大好于基于SQL Server数据库的实现.考虑到磁盘读写远远慢于内存操作,GraphLab在完全没有磁盘访问的情况下,这样的性能差距并不意外.从另一方面看,将数据放在内存中从而完全避免磁盘操作,并不是图数据的专利.在近些年,随着内存容量不断扩大,内存价格不断走低,越来愈多的内存型关系数据应运而生.传统商业数据库也开始逐步将内存数据库的概念、技术融入到其存储、查询引擎中.可以预见,随着内存技术在关系数据库中成熟,图7中的性能差距会越来越小,甚至消失.

图7 GraphLab内存和SQL Server数据库PageRank性能比较Fig.7Performance comparison between GraphLab-memory and SQL Server

4 结论

本文提出了一种基于关系数据库的图计算平台.该平台将图的拓扑结构以邻接表的形式存储在表格中,从而达到了和原生图计算平台相同的数据格式.在此基础上,利用SQL语句丰富的表达力,将BSP编程模型下的图算法简洁、准确地表达出来.SQL语句进而被关系数据库高效地执行,最终将图计算结果返回.实验结果表明,基于关系数据库的图计算与原生图平台比较起来,在很多方面都有性能优势.目前存在的性能局限,和图数据本身并无关系.随着关系数据库的发展、演化,这些局限最终都可以被弥补、消除,在各类场景下提供高效的图计算支持.

［1］GONZALEZ J E,LOW Y,GU H J,et al.PowerGraph:Distributed graph-parallel computation on natural graphs[C]//Proceedings of the 10th USENIX Conference on Operating Systems Design and Implementation. 2012:17-30.

［2］KYROLA A,BLELLOCH G,GUESTRIN C.GraphChi:Large-scale graph computation on just a PC [C]//Proceedings of the 10th USENIX Conference on Operating Systems Design and Implementation.2012: 31-46.

［3］LOW Y,GONZALEZ J E,KYROLA A,et al.GraphLab:A new framework for parallel machine learning[J]. Computer Science,2014:arXiv:1408.2041[cs.LG].

［4］VALIANT L G.A bridging model for parallel computation[J].Communications of the ACM,1990,33(8):103-111.

［5］MALEWICZ G,AUSTERN M H,BIK A J C,et al.Pregel:A system for large-scale graph processing [C]//Proceedings of the 28th ACM Symposium on Principles of Distributed Computing.2009:6-16.

［6］Kamvar S,Haveliwala T,Golub G.Adaptive methods for the computation of PageRank[J].Linear Algebra and its Applications,2004,386:51-65.

(责任编辑:李艺)

A RDBMS-based graph computing platform

JIANG Kui1,CHEN Liang2
(1.Hebei Vocational College of Rail Transportation,Shijiazhuang,050021 China; 2.Microsoft Research Asia,Beijing100080,China)

This paper proposes a new RDBMS-based(relational database management system)graph computing platform.In this platform,graph data is represented in native data structures,achieving the same representation as in native graph computing systems. On top of this native representation,graph algorithms are expressed as SQL(Structured Query Language)statements,which are executed by the underlying relational database systems.Experimental results show that this new graph computing platform leverages mature SQL technologies on query optimization and execution,thereby providing superior performance in many aspects.Its current performance limitations,on the other hand,will be overcome by future evolution and optimization of relational database systems.

RDBMS(relational database management system);graph computing; native graph computing platforms

TP392

A

10.3969/j.issn.1000-5641.2016.05.012

1000-5641(2016)05-0103-09

2016-05

蒋奎,男,高级讲师,研究方向为铁道车辆及铁道信息系统.E-mail:mwong56@gmail.com.

陈亮,男,研究员,研究方向为数据库及信息系统.E-mail:jeche@microsoft.com.