Multiplex 网络上的平均吸收时间*

王 燕

(广东技术师范学院)



Multiplex 网络上的平均吸收时间*

王 燕

(广东技术师范学院)

针对规则的Multiplex 网络，通过循环矩阵的知识得到了平均吸收时间与耦合强度λ的递减函数.无论λ取何值，带有吸收点的Multiplex 网络上的平均吸收时间均将介于单独考虑两层网络时得到的相应量之间，这些结果都和已有文献的结论明显不同.

Multiplex 网络; 转移概率矩阵; 平均吸收时间

0 引言

复杂网络上的随机游走是当前学术界研究的热点问题,一方面随机游动行为特征深受复杂网络拓扑结构的影响，另一方面复杂网络的结构特征也可由随机游动来探索揭示，其中精确计算带有吸收点的随机游走过程的平均吸收时间(ATT)是该领域的一个难点，这里的ATT 定义为从网络上任意一个节点出发首次到达设定陷阱的平均时间.带有陷阱的随机游走过程和其它动力学过程有紧密的联系，它是衡量吸收有效性的一个指标，为了获得ATT 指标与网络规模或其他参数之间的关系，最近几年针对不同的网络结构，涌现出了一系列求解ATT 的研究成果[1-2].然而这些工作大部分都只是解析单个网络上的ATT问题，对于相互有关联的多部分网络或Multiplex 网络[3]上该问题的研究相对较少.此处multiplex 网络是指具有不同网络结构的两个单层网络相互耦合而成，耦合强度为 .在允许同层网络相异点间和异层网络对偶点间可以相互转移的条件下，文献[4]给出了Multiplex 网络上ATT 的解析式，并分析了耦合强度λ对ATT的影响.假设允许一步可以直接从网络中一点转移到异层网络中的相异点，笔者重新考虑了Multiplex网络上的ATT问题.并以规则的Multiplex网络为例，从ATT的精确表达式中得到ATT为λ的递减函数，与文献[4]的结果有明显不同.

1 精确求解Multiplex网络中的ATT

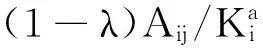
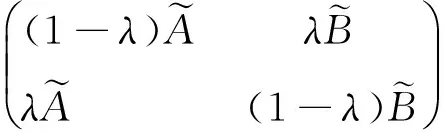
(1)

(2)

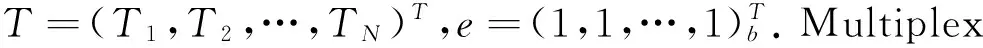
(3)

(4)

其中

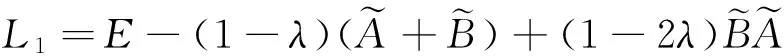
(5)

因此考虑Multiplex网络上的随机游走问题，当允许walker一步可以直接从网络中一点转移到异层网络中的相异点时，方程(4), (5)给出了ATT的精确结果.

2 规则Multiplex 网络中的ATT

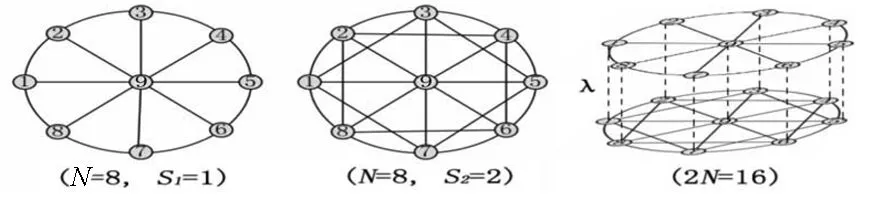
图1 N表示吸收点N+1节点有N个邻居，s表示每个非吸收点有2s个最近邻邻居

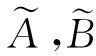
(6)

从方程(6)知，ATT独立于网络尺寸N，并且是关于耦合强度λ的递减函数.即λ越大，越能有效地阻碍扩散过程的传播范围.进一步按照相同的方法，容易得到单层网络上的ATT分别为1+2s1,1+2s2.

比较Multiplex网络上的ATT结果(6)与单独考虑两个单层网络上的ATT的大小.此处假设s1

(7)

在两个单层网络上加入吸收点取得的阻碍效果仅与该wheel网络的参数si有关.其越小，阻碍效果越好(ATT是si的递增函数).进一步，从式(7)得知，在对Multiplex 网络加入吸收点时，阻碍有效传播的效果介于在两个单层网络中加入吸收点的效果之间.参 考 文 献

[1] Nicosia V, Bianconi G, et al. Growing multiplex networks [J]. Phys. Rev Lett, 2013(111): 058701.

[2] Agliari E. Exact mean first-passage time on the T graph [J]. Phys Rev E, 2008(77): 011128.

[3] Hwang S, Lee D S, et al. Effective trapping of random walkers in complex networks [J]. Phys Rev E, 2012(85): 046110.

[4] Ma Y F, Jiang X, et al. Trapping on deterministic multiplex networks [J]. Acta Physica Polonica B, 2015, 4 (46): 789.

[5] Davis P R. Circulant matrix [M]. New York: John Wiley & Sons, 1979.

(责任编辑：季春阳)

Mean Trapping Time of Random Walk on a Multiplex Network

Wang Yan

(Guangdong Polytechnic Normal University)

For the deterministic multiplex network, we get the accurate function expression of ATT by using the knowledge of the circulant matrix, which is different from the results of the reference. ATT of the multiplex network is between the corresponding qualities when we consider two layer network independently, regardless of the value of the coupling strength.

Multiplex network; Transition matrix; Average trapping time

2016-02-22

*广东省普通高校青年创新人才项目(2015KQNCX088)

N94, O29

A

1000-5617(2016)02-00