估计Logistic模型中的参数

徐 萍

(哈尔滨远东理工学院)



估计Logistic模型中的参数

徐 萍

(哈尔滨远东理工学院)

Logistic模型是广义线性模型的一种，其用途广泛，该文将利用差分法对其进行分析，并且运用Logistic模型解决实际问题.

Logistic模型；广义线性模型；差分法

0 引言

Logistic曲线方程是1938年生物数学家VerhulstP F为研究人口增长过程而推导出的重要的方程，但由于种种原因，被长期湮没，直到20世纪20年代才被Pearl R和Reed L T重新发现并应用.Logistic曲线方程不仅应用于社会经济现象方面，也广泛应用于动植物繁殖过程和生长发育等领域的研究.该文就Logistic模型中的参数进行分析，根据实例得出参数的具体算法，给出结论.

经典的Logistic模型[1]为

(1)

其中,k为环境最大容量，r为种群的内禀增长率,x为种群的生长量,dx/dt为种群的变化率.并且t≥0,r>0,k>0.该文仅对二参数Logistic模型进行研究，因此下面对两个参数k和r分析.

1 差分法估计参数k和r

Logistic模型在现实生活中有很大的用处.不仅可以用来寻找某一疾病的危险因素，还可以进行预测判别.在这里，将通过具体问题对Logistic模型进行分析 ，来说明实际数据与所建模型是否相容.

由上述Logistic的模型(1)可得

(2)

那么将上式(1)代入，可得

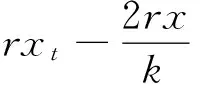
当该式为零时,解算出自变量的解为x1=0,

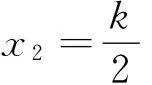
若取样时间h是等距的，即xi=x0+ih(i=0,1,2,…,n)，其中x0为初始时间，则其一阶向前差分公式和k阶向前差分公式分别为：

Δfi=fi+1-fi(一阶向前差分)

Δkfi=Δk-1(Δfi)=Δk-1fi+1-Δk-1fi(k阶向前差分)

若求出一阶差分和二阶差分，那么就可以根据差分的最大值利用插值法进而求出拐点处的最大值，从而求出参数k的值.接下来根据具体事例对上述公式和方法进行分析验证.

数据选择黑龙江省林科院动物所与哈尔滨动物园对人工育出的丹顶鹤雏鸟体重测定值，现对其进行分析，根据体重值得出其一阶差分和二阶差分值，其具体数据见表1.

表1 丹顶鹤雏鸟体重值及其差分值

则由表1分析可得，一阶差分的最大值为雏鸟第40天和第50天的体重的差分值得出的，用Δx5表示，则Δx5=1319.9，那么对应此一阶差分的值，其二阶差分Δ2x4=138.2>0,Δ2x5=-171<0，因此需要用到Newton向前差分公式.

对于只有两个节点x4,x5的函数，因为其最大值点在期间，因此令xm=x4+sh，那么向前差分公式为：

N(x)=f(x4)+sΔy

则得到因变量的最大值为

那么

k=2xm=6584.9>max(xi)=5578.8.

因此k足够大，满足与丹顶鹤雏鸟体重生长实测数据的相容性条件.

下面对内禀增长率r进行估计分析，由于x的对数函数lnx对t的一阶微分[5]为

那么将式(1)代入，则上述方程变形得到：

(3)

则求参数r的问题就转化为求方程(3)的最小二乘解的问题，可以用向前差分法近似求解，具体过程为：

设(ti,xi)(i=0,1,2,…,M)为方程(3)的M+1对实测数据，则t=ti处一阶导数可以用前差商[6]近似，则有

由于k值的取得上面已经给出具体算法，M为实测数据的数量值，因此，只要求出使得该式取得最小值时的r值，便可得出Logistic模型的具体公式.模型是针对实际问题最重要的数学手段,但在现实生活中,存在很多因素是不可避免的,例如在logistic模型中的环境最大容量k，它并不能消除人为因素的影响.上例中，实际数据能与所建模型相容是最希望的.为了避免不相容的情况发生，logistic模型成为检验这类问题的很好的手段.

2 讨论

该文给出了Logistic模型的最简单形式，并且通过差分法和差分公式给出了常数k的求法.利用黑龙江林科院动物所与哈尔滨动物园对人工育出的丹顶鹤雏鸟体重分别在第1、10、20、30、40、50、60、70d的测定值进行差分计算，通过一阶差分和二阶差分对该实例进行计算，得出环境最大容量的值以及种群的内禀增长率的计算公式，从而得出了针对该数据的Logistic模型.实际生活中，由于Logistic模型不仅可以寻找危险因素，预测结果，还可以判别事件发生的概率，该文在计算参数k的时候得出了具体值并且满足与实测数据的相容性条件，因此可取.

[1] 陈元千,胡建国,张栋杰.Logistic模型的推倒及自回归方法[J].新疆石油地质,1991(2).

[2] 殷祚云.Logistic曲线拟合方法研究[J].数理统计与管理,2002(1).

[3] 李荣华.广义差分法及其应用[J].吉林大学自然科学学报,1995(1):26.

[4] 丁恒飞.分数阶偏微分方程的有限差分方法[J].上海大学,2014(4):1.

[5] 郑祖庥.分数微分方程的发展和应用[J].徐州师范大学学报:自然科学版,2008,6:15.

[6] 杨士俊,王兴华.Hermite差值多项式的差商表示及其应用[J].高校应用数学学报A辑:中文版,2006(3):30.Estimate the Parameters in the Logistic Model

(责任编辑：李家云)

Xu Ping

(Harbin Far East Institute of Technology)

Logistic Model is one of the generalized linear model,which owns wide use,The finite difference method should be used to analyze, and the logistic model is used to solve the practical problems.

Logistic Model;Generalized Linear Model;Finite Difference Model

2015-12-30

O212

A

1000-5617(2016)02-0073-02