奇异一阶线性偏微分方程的一种新算法*

高 健，吕学琴

(哈尔滨师范大学)



奇异一阶线性偏微分方程的一种新算法*

高 健，吕学琴

(哈尔滨师范大学)

为研究变系数奇异一阶线性偏微分方程而提出了一种新的算法并且在再生核空间中给出精确解的表达式,其近似解可以由截断级数而得到.在‖·‖W(2.2)(D)的意义下近似解的误差是单调递减的.文中的数值算例说明了该方法的有效性.

近似解；线性偏微分方程；再生核空间.

0 引言

该文研究了如下带有变系数的线性偏微分方程：

A(x,t)Dxu(x,t)+B(x,t)D1u(x,t)+

C(x,t)u(x,t)=F(x,t)

(1)

系数A,B,C和F在点(x,t)=(0,0)∈C2时是奇异的,方程(1)符合以下四个基本条件：

A(x,0)≡0,

(2)

(3)

(4)

C(0,0)≠0.

(5)

注记：情况(2)和(3)表明

A(0,0)=B(0,0)=0,

(6)

在文献[1]中,作者证明了在(2)～(5)的条件下解u(x,t)的存在唯一性.

在最近几年,由Zhou[2]提出的微分转换概念(DT)作为解决偏微分方程的一种最有效的方法而得到广泛关注.多网格法是解决偏微分方程最有效方法之一,在20世纪60年代首次出现并且从20世纪80年代后快速发展,详见文献[8-9].瀑布型多重网格方法是多重网格方法的一种新类型,在文献[11]中提出,文献[12]中的算例证明了这种方法的有效性,作者改进了瀑布型多重网格方法,详见文献[13-14].

在文献[1]中,作者已经研究了变系数奇异一阶线性偏微分方程解的存在性,而在文献中并未对其给出数值算法,因此,该文将给出如上带有条件(2)～(5)的方程(1)的一种新的求解算法.

1 一些再生核空间

1.1 再生核空间W2[-m,m]

W2[-m,m]={u(x)|u,u' 在[-m,m]内是绝对连续的实值函数, u″∈L2[-m,m]},W2[-m,m]中的内积定义为：

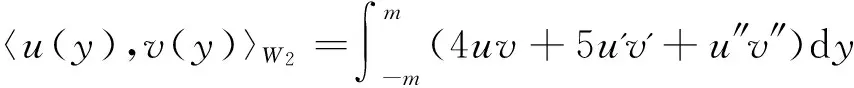
(7)

(8)

再生核Rx(y)的表达式在附录A中给出.

1.2 再生核空间W1[-m,m]

W1[-m,m]={u(x)|u在[-m,m]内是绝对连续的实值函数, u'∈L2[-m,m]},

W1[-m,m]中的内积和范数分别定义为

cosh(|x-y|-2m)].

1.3 再生核空间W(2,2)(D)

命题1.1[16]如果 u(x,t)=u1(x)u2(t),v(x,t)=v1(x)v2(t)∈W(2,2)(D),那么

〈u(x,t),v(x,t)〉W(2,2)=〈u1(x),v1(x)〉W2〈u2(t),v2(t)〉W2.

(9)

命题1.2[16]W(2,2)(D)是一个再生核空间并且再生核为

K(ξ,η)(x,t)=Rξ(x)Rη(t),

(10)

其中Rξ(x),Rη(t)详见(8).类似W(2.2)(D)的定义,可以定义W(1,1)(D)并且W(1,1)(D)是再生核空间.

2 新方法

该节在再生核W(2.2)(D)中给出方程(1)的解.在方程(1)中，

Lu(x,t)=A(x,t)Dxu(x,t)+

B(x,t)Dtu(x,t)+C(x,t)u(x,t),

那么等式(1)可以转化成如下形式：

Lu(x,t)=F(x,t),

(11)

其中L:W(2,2)(D)→W(1,1)(D)是一个有界线性算子.

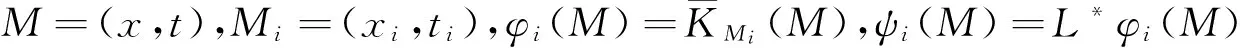
(12)

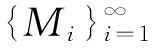
证明 ∀u(M)∈M(2,2)(D),令〈u(M),ψi(M)〉=0,(i=1,2,…),即

〈u(M),(L*φi)(M)〉=〈Lu(M),φi(M)〉=(Lu)(Mi)=0.

(13)

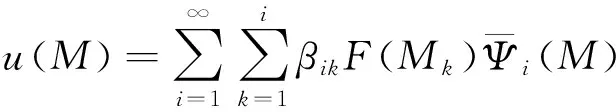
(14)

其中F(M)=A(M)Dxu(M)+B(M)Dtu(M)+C(M)u(M).

∀v(M)∈W(1,1)(D),有〈v(M),φi(M)〉=v(Mi),令u(M)是方程(1)的唯一解,因此有

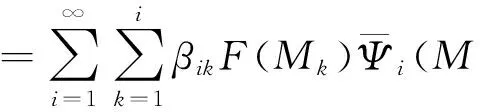
定义u(m)的n项近似解为 un(M)

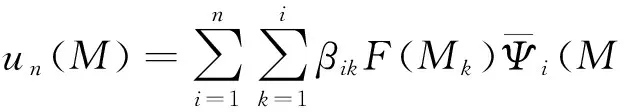
(16)

定理2.3 假设u(M)是方程(1)的解并且rn(M)是un(M)的近似误差,其中un(M)是由(16)给出,那么在‖·‖W(2,2)(D)的意义下误差rn(M)是单调递减的.

证明 由(15)(16),可知

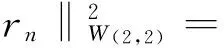
(17)

(17)表明在‖·‖W(2,2)(D)的意义下误差Rn(M)是单调递减的.

3 数值算例

该节通过一些数值算例来证明所提出方法的精确性.在计算过程中,所有的符号和数值计算是由Mathematica5.0演示的.

算例1 考虑方程

A(x,t)Dxu(x,t)+B(x,t)Dtu(x,t)+

C(x,t)u(x,t)=F(x,t)

(18)

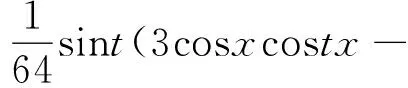
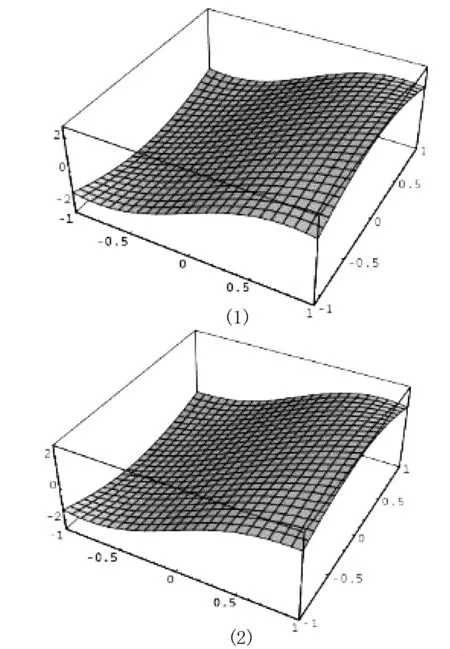
图1 精确解(1)和近似解(2)

3tsinxsintx).精确解u(x,t)=3sinxcosxt,应用该方法在D=[-1,1]×[-1,1]内选取121个点并且在D内得到近似解u121(x,t),数值计算结果见图1.

算例2 考虑方程

A(x,t)Dxu(x,t)+B(x,t)Dtu(x,t)+

C(x,t)u(x,t)=F(x,t)

(19)

其中-1≤t≤1,-1≤x≤1,A(x,t)=2-6sint,B(x,t)=xt2,C(x,t)=cost+xt,F(x,t)=t2xcost+txsint+costsint,真解u(x,t)=sint.应用该方法在D=[-1,1]×[-1,1] 内选择121个点并且在D上得到近似解u121(x,t),数值计算结果见表1.

表1 u(x,t)与un(x,t)的误差比较

4 附录

再生核空间W2[-m,m]

定理4.1 W2[-m,m]是一个再生核空间, ∀u(y)∈W2[-m,m]和定点x∈[-m,m],∃Rx(y)∈W2[-m,m],其中y∈[0,1],例如(u(y),Rx(y))W2[-m,m]=u(x),再生核Rx(y)可以表示为

(20)

证明 (u(y),Rx(y))W2[-m,m]=

假设Rx(y)满足下面的广义微分方程：

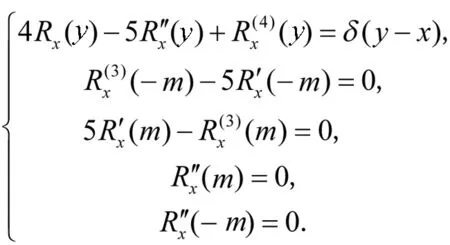
(21)

接下来,将会得到再生核Rx(y)的表达式.

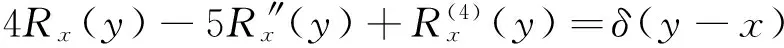
将Rx(y)表示为

Rx(y)=

(22)

由再生核空间 W2[-m,m]的定义,系数 c1,…,c4,d1,…,d4满足

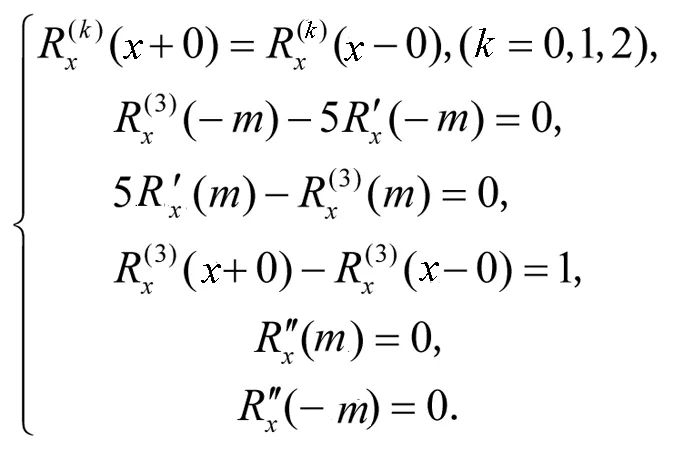
(23)

即可得到(21)的系数.

[1] Masaki Hibino. Borel summability of divergent solutions for singular first-order partial differential equations with variable coefficients. Part I, J Di-fferential Equations,2006, 227(2):499-533.

[2] Ayaz F. On the two-dimensional differential transform method. Appl Math Compu,2003, 143(2-3):361-374.

[3] Ayaz F. Solution of the system of differential equations by differential transform method. Appl Math Compu,2004,147(2):547-567.

[4] Biazar J, Ebrahimi H. An approximation to the solution of hyperbolic equ-ations by Adomian decomposition method and comparison with characteristics met-hod. Appl Math Compu,2005,163:633-638.

[5] Chen C K, Ho S H. Solving partial differential equations by two-dimens-ional differential transform method.Appl Math Compu,1999,106(2-3):171-179.

[6] Jang M J, Chen C L, Liu Y C.Two-dimensional differential transform f-or partial differential equations.Appl Math Compu,2001,121(2-3):261-270.

[7] Yang Xiaofan, Liu Yaoxin, Bai Sen. A numerical solution of second-order li-near partial differential equations by differential transform. Appl Math Compu, 2006,173:792-802.

[8] McCormics S(Ed.). Multigrid Methods. SIAM, Philadelphia, PA, 1987.

[9] Bramble J H. Multigrid Methods, Pitman Research Notes in Mathematics Series (Longman Sci. Tech, London). Copublished with Wiley, New York, 1993.

[10] Xu J. Iterative methods by space decompasition and subspace correction.S-IAM Review,1992,34(4):581-613.

[11] Deuflhard P. Cascadic conjugate gradient methods for elliptic partial dif-ferential equations, in: D.Keys,J.Xu(Eds.),Proc of DDMT, AMS, Providence, 1994,30:29-42.

[12] Bornemann F A, Deuflhard P. The cascadic multigrid method for elliptic prob-lems. Numer Math,1996,75:135152.

[13] Shi Z, Xu X. Cascadic multigrid method for parabolic problem. J C M,2000,815:551-560.

[14] Shi Z C, Xu X J. A new cascadic multigrid Sci, 2001,44(1):21-30.

[15] Li Chunli, Cui Minggen. The exact solution for solving a class nonlinear operator equations in the reproducing kernel space. Appl Math Compu, 2003,143(2-3):393-399.

[16] Aronszajn N. Theory of Reproducing kernel. Trans, A M S, 1950,68:337-404.

(责任编辑：季春阳)

New Algorithm For Singular First-Order Linear PartialDifferential Equations

Gao Jian, Lv Xueqin

(Harbin Normal University)

In this paper, a new method is given in order to solving singular first-order linear partial differential equation with variable coefficients. Represen- tation of the exact solution is given in the reproducing kernel space. Its app- roximate solution is obtained by truncating the series. The error of the app- roximate solution is monotone deceasing in the sense of . The numerical experiment shows that the new method given in the paper is valid.

Approximate Solution; Linear Partial Differential Equation; Reproducing Kernel Space.

2016-01-19

*国家自然科学基金项目(11401145)

O241

A

1000-5617(2016)02-0008-04