一种散乱分层点云的有序化精简方法
解则晓, 刘静晓, 潘成成, 张梦泽
(中国海洋大学工程学院,山东 青岛 266100)
一种散乱分层点云的有序化精简方法
解则晓, 刘静晓, 潘成成, 张梦泽
(中国海洋大学工程学院,山东 青岛 266100)
针对激光扫描仪所得点云散乱分层的特点,提出一种有序化的精简方法。首先基于已知标记点建立三维R-tree和八叉树集成的空间索引,快速准确地获取局部点云数据,保证良好的数据检索效率。然后根据局部点云数据的参考平面法向量信息,选取工件坐标系中的一个坐标轴作为参数化的方向,对局部点云数据进行参数化并拟合二次曲面。最后对R-tree叶节点内的二次曲面进行有序化采样,使散乱分层的点云变为单层,得到整个型面的有序参考点集。应用实例表明,该方法适用于大规模的、具有复杂几何特征且存在一定程度散乱分层的点云,可以有效地提高数据点的整体精确度,且不会丢失点云的细节特征,具有较强的实用性。
数据精简;有序化;散乱分层点云;标记点;3D R-tree
逆向工程在现代制造业中占据着重要的地位,三维数字化技术是逆向工程中的首要环节。作为三维数字化技术的重要组成部分,三维数据精简能够提高曲面建模的质量和效率,具有十分重要的研究意义。
近年来激光扫描系统以其非接触、灵活、高速的优点得到了快速的发展,并广泛应用于航空航天、汽车工业、生物医学等工程领域。激光扫描系统可以快速获取待测表面的激光数据,经其测得的点云数据密度高、数量大,存在大量的冗余数据。此类点云数据直接用来建模会占用大量的存储空间和建模用时,从而降低了建模质量和效率。因此在保证建模精度的同时提取点云数据中反映曲面特征的点、去除冗余数据即数据精简,有助于提高建模效率,是逆向工程中的一项关键技术[1]。
在激光扫描系统扫描过程中,对于工件的平缓表面部分,从单一方位一次扫描就可以得到体现其表面特征的数据点,此类数据点在其局部参考平面的法向量方向上表现为单层;而对于工件的复杂表面部分,必须从不同方位多次扫描才能得到充分的数据点,由于模型的复杂性和测量精度的局限性[2],不同方位扫描得到的数据点被统一到同一三维坐标系下后,会在点云的局部型面的法向量方向上表现出一定程度的散乱分层。
目前国内外数据精简技术大多是针对单层点云提出。如 Weir等[3]提出的包围盒法简单高效,但是选取靠近包围盒中心的点来代替该包围盒中的所有点,无法保证精简后的点云保持初始的曲面特征。Martin和Varady等[4]提出的基于“中值滤波”原理的均匀网格法,该法需要将点云空间分割成均匀网格,确定点云投影面,计算网格中数据点到投影面的距离,选择距离居中的数据点代替网格中其他点,该法多应用于点云曲面垂直于坐标轴的情况,运算速度快,但对于具有复杂曲面的点云精简效果不佳。Lee等[5]提出的三维网格法可以用于表面特征复杂的点云,但首先要对点云进行三角网格化处理,再根据向量加权算法对已生成的三角网格进行删除,运算过程较为复杂。Lee和 Huang[6]采用 K均值聚类的自适应精简算法,该算法能够合理分布点云数据,但是对噪声敏感。陈璋雯和达飞鹏[7]提出的基于模糊熵迭代的精简算法,本质上属于曲率采样法,需要求取每个数据点的曲率,根据数据点曲率计算点云最小模糊熵,由模糊熵决定曲率划分阈值,对于曲率小于阈值的数据点进行稀释,大于阈值的数据点重新进行模糊熵迭代。该方法虽然能保留点云细节特征以逼近点云原型,但是算法效率不高。
本文研究的点云数据来自一种新型激光扫描仪——基于标记点的流动式三维扫描仪[8],该扫描仪利用标记点对系统进行实时定位,将提取的激光数据转换到固定的工件坐标系下。其测量过程是一个不断将激光数据向工件坐标系转换的过程,最终可以得到整个工件的点云数据。当在不同高度不同角度对复杂工件的某个部位进行扫描时,测得的激光数据被转换到工件坐标系下后会表现出一定程度的散乱分层。这类点云几何特征复杂、存在大量冗余数据且表现出一定的散乱分层,既不能直接用于模型重建,用已有的精简算法又难以达到理想的精简效果,因此针对具有该特点的点云,提出一种散乱分层点云有序化精简算法。
本文方法主要分3步进行:
(1) 建立点云的空间拓扑结构,即空间索引的建立。考虑到基于八叉树的R-tree索引[9-11]能够提供稳健高效的空间查询能力,针对流动式三维扫描仪在测量中所使用的标记点的三维坐标精确已知[12-15],且标记点均匀分布的特点,提出了一种基于已知标记点建立点云空间索引的方法:①对点云空间进行三维网格划分,以包含标记点的三维网格为中心对所有的三维网格而非数据点进行聚类;②对于包含数据点的三维网格,根据设定的扇出条件对其进行八叉树分裂,直至所有的叶节点都收敛。该索引结构的创建速度快,叶节点无重叠,便于快速准确地获取局部点云数据。
(2) 确定参数化和采样方法,拟合二次曲面。针对曲面特征复杂的点云数据,提出一种局部点云参数化的方法。获取以 R-tree的叶节点为中心的27个相同大小的空间网格内的数据点,将其作为局部点云数据拟合参考平面,根据参考平面的法向量方向确定点云数据参数化和有序化采样的方向,对局部点云进行参数化后并拟合二次曲面。
(3) 对拟合的二次曲面进行有序化采样。根据局部参考平面的方向量信息,提出一种双有序的采样方法。根据采样点与 R-tree页节点的位置关系决定其取舍,最终可得到整个型面的单层有序点集。
实验结果表明该精简算法效率高,能够在较高程度上保持点云原有的几何特征,且不会丢失点云的细节特征,精简后的点云空间分布均匀有序,能够大幅改善散乱分层点云的偏差,整体上提高数据的精确度。
1 有序化精简算法
针对散乱分层点云的有序化精简算法主要由3部分组成:建立散乱分层点云的空间拓扑结构、局部二次曲面的拟合和有序化采样。算法流程如图1所示。
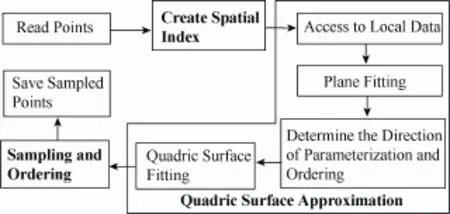
图1 算法流程图
1.1 散乱分层点云空间拓扑结构的建立
点云的局部数据点能够反映工件的局部型面几何特征,因此快速准确地获取局部点云数据,是点云有序化精简的首要问题。本文借助已知标记点对点云建立三维 R-tree和八叉树集成的空间索引。基于已知标记点对三维网格而非数据点进行聚类,然后对三维网格进行八叉树分裂,使该空间索引结构兼具静态方法的高效性和动态方法的灵活性。
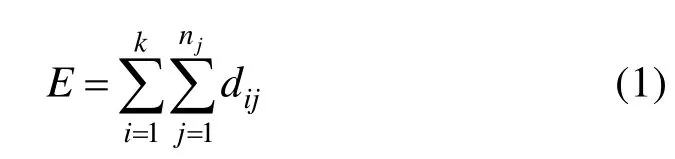
聚类完成后形成k个紧凑独立的立方体簇,每个立方体簇外接空间矩形则为 R-tree的一级内部节点。通过计算得到每个立方体中数据点的个数,将包含数据点的立方体作为 R-tree的二级内部节点。设定扇出参数,即每个节点允许包含的最大和最小数据点个数,采用八叉树剖分各立方体,直至所有的叶节点收敛。叶节点收敛条件为:叶节点中数据点个数小于最大数据点个数或边长等于最小网格尺寸slmin。图 2为一工件实物图及采用标记点建立点云的三维R-tree空间索引结构。
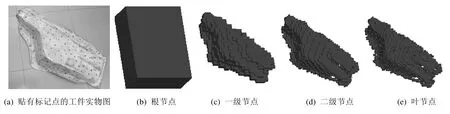
图2 工件实物图与工件点云的三维R-tree结构
1.2 局部二次曲面的拟合
1.2.1 局部点云数据的参数化
分层点云的局部数据点沿其参考平面法向量方向是散乱分层的,所以描述同一局部特征的数据点会分布在相邻的 R-tree叶节点中。以相邻叶节点中的任意一个为中心,由该叶节点及与之邻接的26个同等大小的立方体构成的立方体空间,都包含另一个相邻叶节点,因此其内部的数据点可以完整描述点云的局部型面特征。本文以叶节点为中心的 27个立方体空间中的数据点集{Ni},i=1,2,…,k 作为局部点云数据。
由于二次曲面是局部坐标下的参数表示,需要建立局部坐标系。首先利用局部点云数据拟合参考平面,得到单位法向量n。然后将叶节点为中心的 27个立方体空间的起始点(xo,yo,zo)作为局部坐标系的原点。最后选取 3个工件坐标轴中与参考平面法向量n夹角最小的一个,作为局部坐标系的Z轴方向,建立局部坐标系oxyz。如在图3(a)中,参考平面的法向量n与工件坐标系的zw轴的角度最小,则局部坐标系的z轴与zw轴同向。局部坐标系与工件坐标系的关系为:

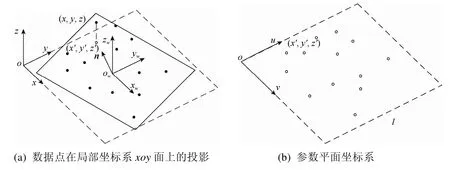
图3 参数平面坐标系的建立
参考累加弦长参数化的方法[17],将局部点云数据作如下参数化:①以局部坐标系原点为原点,局部坐标系x轴和y轴为u轴和v轴,建立参数平面坐标系ouv,如图3(b)所示。②确定以R-tree的叶节点为中心的 27个立方体空间的边长l。最终计算局部点云数据的参数值,{Ni}为点云的局部数据点集,Ni在局部坐标系下的坐标为(xi,yi,zi),那么Ni的参数值为。
1.2.2 局部二次曲面
本文采用二次参数曲面来近似表示任意复杂型面的局部形状。二次参数曲面方程为:,其矩阵形式为:

其中,Q是3×3矩阵,其元素是矢量值Qij,。
引入9R空间矢量:
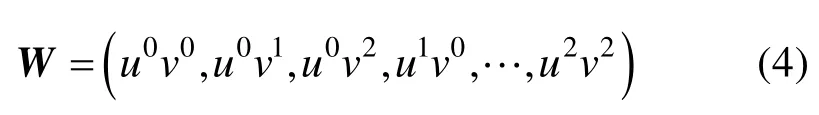

利用 2.1节得到的局部数据点集{Ni}的局部坐标系坐标(xi,yi,zi)及参数值(ui,vi),引入矢量,其中,,,,并将Q重写为Q=(a b c),那么逼近的二次曲面与数据点的误差函数为:

二次参数曲面的拟合就是使误差函数最小化的过程(图4),即使局部点云数据与二次参数曲面对应点之间的欧几里德距离的平方和最小[18]。通过推导,得到系数矩阵Q的表达式:
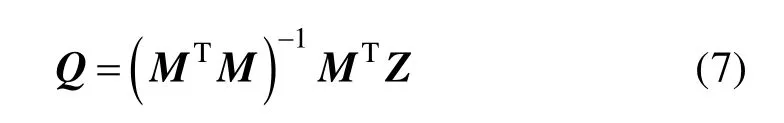

图4 局部数据点拟合二次曲面示意图
1.3 有序化采样
局部二次曲面可以准确地描述复杂型面的局部形状,因此对局部二次曲面进行采样得到的数据点可以作为点云隐含型面上的参考点。为了使参考点在点云型面上的分布均匀有序,本文提出一种有序化的采样方法。该方法是一种对点云数据进行局部双向有序化的过程,具体方法是依据点云局部参考平面的法向量信息,从不同的坐标轴方向对局部二次曲面进行采样。比如工件坐标系的xw轴(yw轴或zw轴)与点云局部参考平面法向量的夹角最小,则将叶节点的中轴线定义为过叶节点中心并与xw轴(yw轴或zw轴)平行的直线。计算叶节点的中轴线与局部二次曲面的交点,如果交点位于叶节点的内部,那么将该交点作为点云的有序参考点;否则,该交点将不被采用。
由局部坐标系和工件坐标系的关系可知,在工件坐标系下,无论叶节点的中轴线方向如何,其在局部坐标系下都与z轴同向,如图4所示。因此有序化采样的计算过程为:令 u= 0.5, v= 0.5,按式(4)求取W,那么中轴线与局部二次曲面在局部坐标系下的交点 r(u, v),可由

得出。将交点 r(u, v)转换至工件坐标系下,就可以得到点云型面上的一个有序参考点。
由于有序参考点是叶节点的中轴线与局部二次曲面的交点,可根据叶节点中轴线的方向即与工件坐标系的xw轴、yw轴或zw轴平行,将参考点的有序类型分为yz有序、zx有序或xy有序。经有序化采样得到的参考点集,在由同一有序类型的参考点组成的非临界区域,参考点在其有序方向上等间隔均匀分布;在不同有序类型区域间的临界区域则由不同有序类型的参考点平滑过渡(图5)。
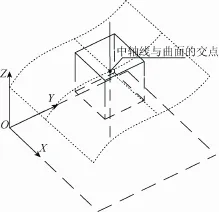
图5 有序化采样示意图
2 实验与分析
为验证本文提出的方法的可行性,使用基于标记点的流动式三维扫描仪采集了 3个不同工件的点云数据,分别从大规模数据精简、算法精度及大曲率数据精简等3个方面进行了实验。
2.1 大规模数据精简实验
为验证算法具备精简大规模数据的能力,选取图2(a)中工件的点云进行精简实验,工件尺寸为1047.6 mm×512.1 mm×317.7 mm,点云的数据点数量为4 272 370个,由图6可明显看出,工件的点云含有大量冗余数据,数据点空间分布不均匀,通过局部放大图可以看出数据点的空间分布散乱无序,并存在一定程度的分层。为了同时验证算法的精简效果及效率,将本文算法与文献[4]中的均匀网格法和文献[7]中的曲率采样法的精简结果进行对比。实验中将最小网格尺寸设置为3 mm。
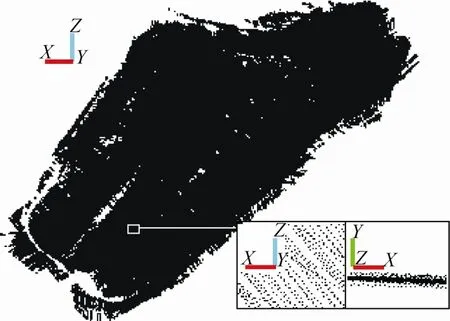
图6 工件点云及局部放大效果图
分别使用 3种方法对工件的点云隔点读取后进行精简运算,精简后点云效果图如图 7所示。由图7可知3种方法所得点云的数据冗余情况较于精简前都有了很大的改善,基本上消除了分层,但前两种方法所得点云仍散乱无序,而本文方法所得点云空间分布均匀有序。将 3种方法所得点云进行三维网格化并平滑着色,可以看出经本文方法精简后工件表面较于其他两种方法更加平整光滑。由表1可知,采用本文方法对400多万点云数据进行精简,精简率达到 98%以上,所用时间为127.61 s,在3种方法中用时最短,证明本文算法的速度较快。综合分析图7和表1可知,本文方法在保证精简后曲面平滑度的前提下能够满足点云精简率和精简速度的要求,表明本文算法实用有效,精简效果好,精简效率高。

图7 不同方法所得点云及着色图
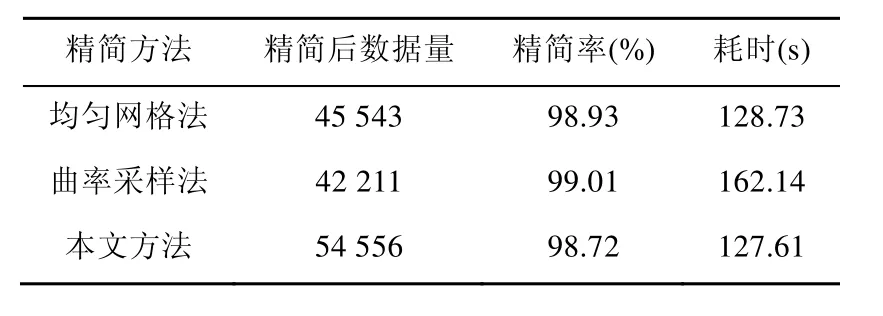
表1 不同方法对大型工件点云精简结果比较
2.2 算法精度验证实验
为验证本文算法的精度能够满足应用要求,用扫描仪对一个球体(图8)进行扫描,分别利用不同方法对得到的球面点云进行精简,在逆向工程专业软件Imageware12.1中对精简前后的球面数据点拟合球体,对比不同方法所得点云拟合球体的几何特征及点云到拟合球体的几何偏差,并给出点云到拟合球体的偏差分布图。实验中将最小网格尺寸设置为1 mm,实验结果如表2及图9所示。
由图9可知,由于存在测量误差,初始点云到拟合球体的偏差分布非常不均匀,且整体上偏差较大。采用不同方法精简后,点云偏差分布都得到明显的改善,但是前两种方法的球面上正负偏差交叉分布,且球面上存在偏差较大的点。经本文方法精简后的点云偏差较于前两种方法更为均匀,大部分偏差保持在0.1 mm以内,球面上不存在偏差较大的点,点云的整体球面度较好。

图8 球体实物图
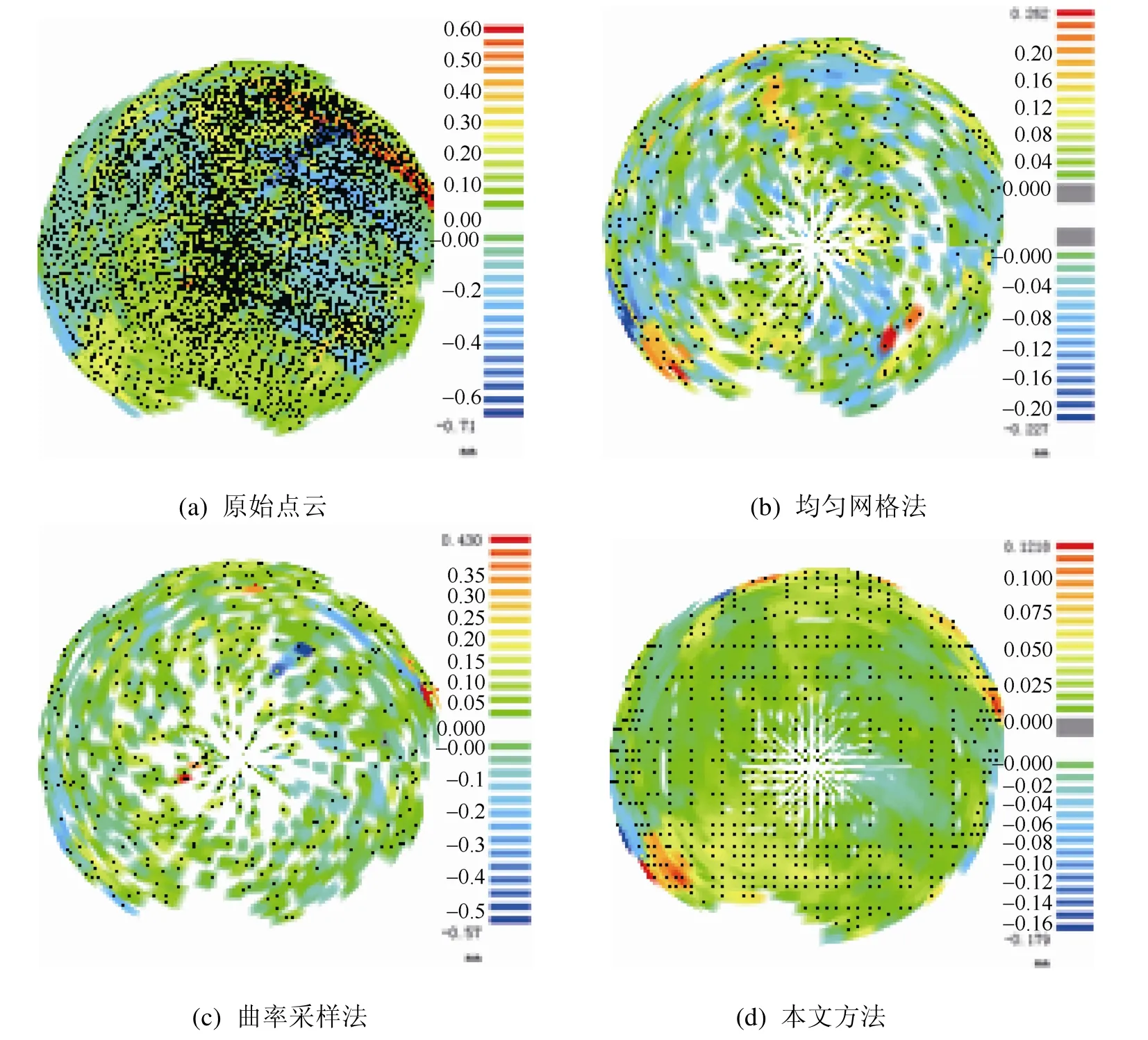
图9 点云到拟合球体偏差分布图

表2 不同方法对球体点云精简效果对比
由表2可知,3种方法都大幅减少了冗余数据,精简后拟合的球心坐标和球体半径基本保持不变,说明 3种算法都能在较高程度上保持初始点云的几何特征;但是本文方法相对于其他两种方法,得到的型面参考点到拟合球面的几何最大偏差、平均偏差及标准偏差都为最小,说明本文方法对点云偏差的改善更加明显,能够整体上提高数据的精确度。
2.3 大曲率数据精简实验
工件型面大曲率区域的点云精简效果是检验精简算法的重要标准之一,为验证算法对大曲率区域点云精简的有效性,选取一个矩形工件对其棱线区域进行扫描,如图10所示。棱线区域的型面特征满足大曲率的特点,利用本文提出的算法对该区域的点云进行精简,将精简前后的点云效果进行对比,并给出精简前后棱线处点云的截面效果图。实验中将最小网格尺寸设置为0.6 mm。

图10 矩形工件的待扫描棱线区域
通过图11可以看出,精简后的点云完整地保留了棱线特征。点云在棱线处的数据点在工件坐标系下为有序化的临界区域,精简后棱线区域的上表面数据点的有序类型为xy有序,侧面数据点为yz有序,棱线处则由以上两种类型的有序点自然过渡。
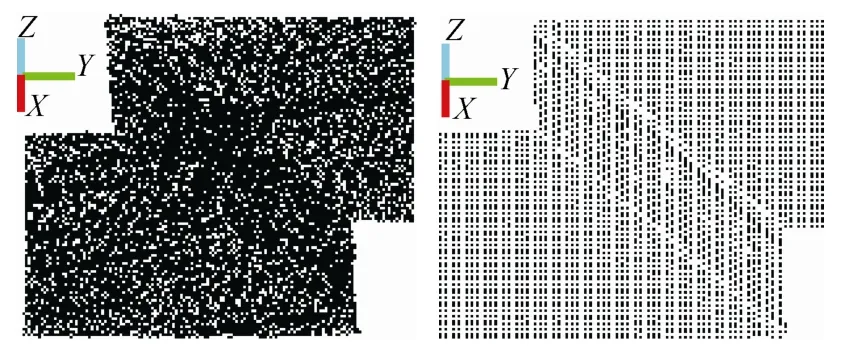
图11 棱线区域精简前后点云对比图
精简前后点云棱线处的横截面如图12所示,截面宽度约为0.5 mm。可以看出,精简之前棱线处点云散乱分层,特征模糊。通过精简,棱线特征辨识度提高,数据点变为单层有序点集,较好地保留了大曲率区域点云的细节特征。

图12 棱线区域精简前后截面对比图
3 结 论
针对激光扫描仪测量误差带来的点云散乱分层的问题,提出了一种有序化精简方法,该方法适用于大规模的,具有复杂几何特征的散乱分层点云的精简:①基于已知标记点建立三维 R-tree和八叉树集成的空间索引,该索引便于快速准确获取局部点云数据;②利用局部二次曲面逼近局部数据点并对其进行采样,可以有效地降低点云的几何偏差,提高数据点的整体精确度;精简后的点云能在较高程度上保持初始点云的几何特征,且不会丢失大曲率区域的细节特征;③根据局部参考平面的法向量来决定采样方向,可以使整个型面的数据点均匀有序,为点云的后续处理提供了便利。
[1] 范 然, 金小刚. 大规模点云选择及精简[J]. 图学学报, 2013, 34(3): 12-19.
[2] Yau H T, Chen C Y, W ilhelm R G. Registration and integration of multiple laser scanned data for reverse engineering of complex 3D models [J]. International Journal of Production Research, 2000, 38(2): 269-285.
[3] Weir D J, Milroy M, Bradley C, et al. Reverse engineering physical models employing w rap-around B-spline surfaces and quadric [J]. Proceedings of the Institution of Mechanical Engineers, 1996, 210(B2): 147-157.
[4] Martin R R, Varady T. RECCAD, Deliverable Document 1 COPERNICUS Project [EB/OL]. [2015-07-15]. http://ralph.cs.cf.ac.uk/papers/geometry/recrep.pdf#page =119.
[5] Lee K H, Woo H, Suk T. Point data reduction using 3D grids [J]. Advanced Manufacturing Technology, 2001, 18: 201-210.
[6] Lee P F, Huang C P. The DSO feature based point cloud simplification [C]//Computer Graphics, Imaging and Visualization (CGIV), 2011 Eighth International Conference on. New York: IEEE Press, 2011: 1-6.
[7] 陈璋雯, 达飞鹏. 基于模糊熵迭代的三维点云精简算法[J]. 光学学报, 2013, 33(8): 153-159.
[8] 顾 宾. 基于标记点的流动式三维扫描测量技术的研究[D]. 青岛: 中国海洋大学, 2013.
[9] Zhu Q, Gong J, Zhang Y T. An efficient 3D R-tree spatial index method for virtual geographic environments [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2007, 62(3): 217-224.
[10] 龚 俊, 柯胜男, 朱 庆, 等. 一种八叉树和三维 R树集成的激光点云数据管理方法[J]. 测绘学报, 2012, 41(4): 597-604.
[11] 邵正伟, 席 平. 基于八叉树编码的点云数据精简方法[J]. 图学学报, 2010, 31(4): 73-76.
[12] 邾继贵, 郭 磊, 叶声华. 现场条件下大空间三维精密定位原理与方法[J]. 光学学报, 2009, 29(7), 1872-1876.
[13] 张维中, 张丽艳, 潘振宽, 等. 一种基于标记点的近景摄影测量系统[J]. 东南大学学报: 自然科学版, 2006, 36(5): 741-745.
[14] 周 玲, 张丽艳, 郑建冬, 等. 近景摄影测量中标记点的自动检测[J]. 应用科学学报, 2007, 25(3): 288-294.
[15] 解则晓, 高 翔, 崔 健. 移动式三维测量用圆形标记点提取算法[J]. 中国激光, 2013, 40(12): 160-105.
[16] 汪 中, 刘贵全, 陈恩红. 一种优化初始中心点的K-means算法[J]. 模式识别与人工智能, 2009, 22(2): 199-304.
[17] Ma W, Kruth J P. Parameterization of random ly measured points for least squares fitting of B-spline curves and surfaces [J]. Computer-Aided Design, 1995, 27(9): 663-675.
[18] Yang M, Lee E. Segmentation of measured point data using a parametric quadric surface approximation [J]. Computer-Aided Design, 1999, 31(7): 449-457.
A Data Reduction and Ordering A lgorithm for Scattered and Layered Point Cloud
Xie Zexiao, Liu Jingxiao, Pan Chengcheng, Zhang Mengze
(College of Engineering, Ocean University of China, Qingdao Shandong 266100, China)
Concerning the scattered and layered characteristic of point cloud acquired by laser scanners, a data reduction and ordering algorithm is proposed. Firstly the spatial index of point cloud is created based on known marked points using a method integrating Octree and 3D R-tree, ensuring fast and correct access to local data and high efficiency of data retrieval. Secondly one axis of the work coordinate system is selected as the projective direction for parameterizing the local data, which is determined by the normal vector of local reference plane. Then along the selected direction the local data is parameterized and the quadratic surface is approximated. Finally the ordered set of reference points is obtained by sampling the quadratic surface through the R-tree’s leaf nodes, making the scattered and layered point cloud be single layered. Application examples show that the algorithm can improve the overall accuracy of the data as well as maintain the details of point cloud, indicating good validity and practicability in the reduction of scattered and layered large-scale point cloud with complex geometric features.
data reduction; spatial ordering; scattered and layered point cloud; marked point; 3D R-tree
TG 156
10.11996/JG.j.2095-302X.2016030359
A
2095-302X(2016)03-0359-08
2015-08-15;定稿日期:2016-03-13
国家自然科学基金项目(61571408)
解则晓(1968–),男,山东临沂人,教授,博士。主要研究方向为机器视觉和机器人运动控制及机器人测量等。E-mail:xiezexiao@ouc.edu.cn

