一种求解Bose-Hubbard模型的简单方法

张丹伟

(1.华南师范大学物理与电信工程学院，广州510006； 2.广东省量子调控工程与材料重点实验室，广州510006)



一种求解Bose-Hubbard模型的简单方法

张丹伟1，2

(1.华南师范大学物理与电信工程学院，广州510006； 2.广东省量子调控工程与材料重点实验室，广州510006)

针对描述晶格中多体相互作用玻色子体系的Bose-Hubbard模型，首先计算相互作用能与跳跃能比值趋于无穷大和趋于零两种极限的基态，分别得到了莫特绝缘态和超流态两个量子相。其次利用平均场近似引入超流序参量，通过二阶微扰解析计算基态能量，从而得到体系从超流态到绝缘态的量子相变的边界方程。最后通过数值软件求解边界方程得到Bose-Hubbard模型的相图。该求解Bose-Hubbard模型的平均场方法不仅能够得到完整相图，而且整个过程物理图像清晰、简洁明了便于理解。

Bose-Hubbard模型；超流态；莫特绝缘态；平均场近似；相图

引言

在凝聚态物理领域，Hubbard于1963年提出了研究窄带中电子强关联效应的多体相互作用模型[1]，被称为Hubbard或Fermi-Hubbard模型。该模型成功解释了电子材料中电子的关联效应可以导致金属态到莫特绝缘态的量子相变，因此在理论和实验上都受到广泛关注和研究[2-11]。Fisher等人提出Bose-Hubbard模型[12]，用于研究多体相互作用玻色子体系的类似问题。理论上发现，对于周期晶格中具有短程排斥相互作用的玻色子体系，其晶格间跳跃能量与相互作用强度比值的变化会导致体系在超流态和莫特绝缘态之间发生量子相变。由于在研究玻色超流和量子相变等问题具有重要意义，Bose-Hubbard模型一直受到凝聚态物理理论和实验研究人员的广泛关注[13-21]。在求解Bose-Hubbard模型方面，主要有基于格林函数和量子场论等解析方法[13-17]，以及基于量子蒙特卡罗和密度矩阵重整化群等数值方法[18-21]。然而这些求解方法都比较复杂，不容易对Bose-Hubbard模型及其物理图像形成清晰的理解。

本文提出一种基于平均场近似求解Bose-Hubbard模型的简单方法。对于晶格中多体相互作用玻色子体系，首先计算相互作用能与跳跃能比值趋于无穷大和趋于零两种极限的基态，分别得到了莫特绝缘态和超流态两个量子相。其次，利用平均场近似，引入描述超流态的序参量，通过二阶微扰解析计算基态能量，从而得到体系从超流态到绝缘态的量子相变的边界条件方程。最后，通过数值软件求解边界方程得到Bose-Hubbard模型的相图。该求解Bose-Hubbard模型的简单方法不仅能够得到完整相图，而且整个过程物理图像清晰、简洁明了便于理解。

1Bose-Hubbard模型的基态

描述周期晶格中多体相互作用玻色子体系的Bose-Hubbard模型的哈密顿量为[12]：

(1)

(2)

首先考虑相互作用很大的极限，即U/J→∞，此时可以只考虑相互作用项：

(3)

在粒子数表象中，可以写出相应的本征态为：

(4)

其中，M为格点总数。这个基态表明每个粒子都局域于各自的格子中，对应体系处于莫特绝缘态。对产生和湮灭算符做傅里叶变换，即

(5)

可以得到动量空间粒子数的期望值

(6)

(7)

考虑U/J→0情况，此时可以只考虑晶格间的跳跃，即

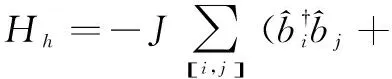
(8)

同样通过傅里叶变换可得

(9)

进一步化简可以得到

(10)

(11)

假如开始时U/J很小，该Bose-Hubbard体系的基态为超流态，随着U/J逐渐增大到某一个临界值时，基态是莫特绝缘态，则体系出现了从超流到莫特绝缘态的量子相变。那么关键问题就是如何求解这个量子相变的边界。利用平均场近似方法简洁有效地计算出相变边界方程以及整个相图。

2平均场方法求解相变边界

(12)

将(12)式代入到方程(1)中，可以得到平均场近似下的Bose-Hubbard模型的简化哈密顿量：

(13)

其中，Z=2d为配位数。平均场近似下的基态为：

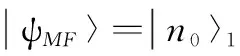
(14)

那么描述每个格点中粒子的哈密顿量为：

(15)

利用二阶微扰求体系的本征能量。把哈密顿量重新写为：

H=H(0)+ψV

(16)

(17)

(18)

另外，可算得二阶近似的本征能量为：

(19)

因此，体系的基态能量可记为：

Eg(ψ)=a0+a2ψ2+O(ψ4)

(20)

其中，零阶和二阶能量泛函为：

为了使体系能量更低，即min{Eg(ψ)}，可以得到：

(1)当a2>0时ψ=0，此时基态为莫特绝缘态。

(2)当a2<0时ψ≠0，说明a2=0是超流态和绝缘态的边界条件。由a2=0可得到

(21)

进一步计算得到边界条件为：

(22)

根据边界条件方程(22)，利用数学软件Matlab求解该方程。编写的Matlab程序语言如下：

clear all;

g=1;

y=0:0.01:1;

x=(g-y).*(y-g+1)./(g*(g-y)+(g+1)*(y-g+1));

plot(x,y);

hold on;

g=2;

y=1:0.01:2;

x=(g-y).*(y-g+1)./(g*(g-y)+(g+1)*(y-g+1));

plot(x,y);

hold on;

g=3;

y=2:0.01:3;

x=(g-y).*(y-g+1)./(g*(g-y)+(g+1)*(y-g+1));

plot(x,y);

hold on;

g=4;

y=3:0.01:4;

x=(g-y).*(y-g+1)./(g*(g-y)+(g+1)*(y-g+1));

plot(x,y);

hold on;

xlabel('ZJ/U');

ylabel('mu/U');

Bose-Hubbard模型的相图如图1所示。在参数区域(J/U,μ/U)中，固定化学势μ而对于不同填充数g，J/U较小时基态为莫特绝缘态而逐渐增大该比值体系可发生相变到超流态，而且莫特绝缘态的参数区间呈现凸显结构，区间随着g增大而减小。此外，当化学势与相互作用能量的比值μ/U为整数时，体系处于绝缘态与超流态的临界，这是因为此时体系基态的最低激发能量刚好为零，即满足方程(20)中a2=0的条件。从图1中可估算，对于填充数为g=1的情况，莫特绝缘区间凸显处对应的相变临界值U/J≈5.8Z，对于g>1的情况，该临界值为U/J≈4gZ。这个完整的相图和边界值与其他解析或者数值模拟得到的结果定量上一致[13-21]。

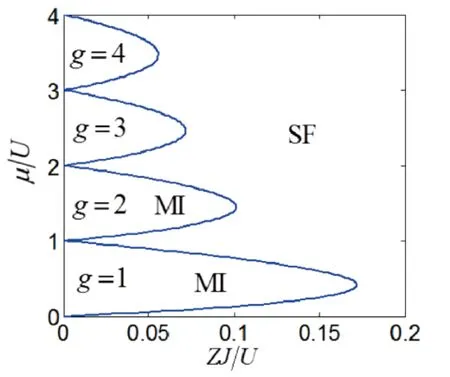
注：其中SF代表超流态，MI代表莫特绝缘态。图1Bose-Hubbard模型的平均场相图

3结论

(1)对于描述晶格中多体相互作用玻色子体系的Bose-Hubbard模型，计算相互作用能与跳跃能比值趋于无穷大和趋于零两种极限的基态，分别得到了莫特绝缘态和超流态两个量子相。

(2)利用平均场近似，引入超流态序参量，通过二阶微扰解析计算基态能量，从而得到体系从超流态到绝缘态的量子相变的边界条件方程。通过数值软件求解边界方程得到Bose-Hubbard模型的相图。

(3)这种求解Bose-Hubbard模型的平均场近似方法不仅能够得到完整相图，而且整个过程物理图像清晰，简洁明了。

[1] HUBBARD J.Electron correlations in narrow energy bands[J].Proc Roy Soc 1963,276(1365):238-257.

[2] 李正中.固体理论[M].北京:高等教育出版社,2006.

[3] 冯端,金国钧.凝聚态物理学[M].北京:高等教育出版社,2013.

[4] SACHDEV S.Quantum phase transitions[M].Oxford:Cambridge University Press,2011.

[5] AFFLECK I,MARSTON J B.Large n limit of the Heisenberg-Hubbard model:Implications for high-Tc superconductors[J].Phys Rev B,1988,37(7):3774-3777.

[6] GEORGES A,KOTLIAR G.Hubbard model in infinite dimensions[J].Phys Rev B,1992,45(12):6479-6483.

[7] MURMANN S,BERGSCHNEIDER A,KLINKHAMER V M,et al.Two fermions in a double well:Exploring a fundamental building block of the Hubbard model[J].Phys Rev Letts,2015,114:Art 080402,5pp.

[8] JOHNSON T H,YUAN Y,BAO W,et al.Hubbard model for atomic impurities bound by the vortex lattice of a rotating Bose-Einstein condensate[J].Phys Rev Letts,2016,116:Art 240402,5pp.

[9] HART R A,DUARTE P M,YANG T L,et al.Observation of anti ferromagnetic correlations in the Hubbard model with ultracold atoms[J].Nature,2015,519(7542):211-214.

[10] 赵红霞,赵晖,陈宇光,等.一维扩展离子Hubbard模型的相图研究[J].物理学报,2015,64(10):213-218.

[11] 张龙,翁征宇.Hubbard模型中的相位弦效应与交互Chern-Simons理论[J].物理学报,2015,64(21):9-23.

[12] FISHER M P,WEICHMAN P B,GRINSTEIN G,et al.Boson localization and the superfluid-insulator transition[J].Phys Rev B,1989,40(1):546-570.

[13] JAKSCH D,BRUDER C,CIRAC J I,et al.Cold bosonic atoms in optical lattices[J].Phys Rev Letts,1998,81(15):3108-3111.

[14] GREUNER M,MANDEL O,ESSLINGER T,et al.Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms[J].Nature,2002,415:39-44.

[16] ZHANG D W,CHEN J P,SHAN C J,et al.Superfluid and magnetic states of an ultracold Bose gas with synthetic three-dimensional spin-orbit coupling in an optical lattice[J].Phys Rev A,2013,88:Art 013612,8pp.

[17] SENGUPTA K,DUPUIS N.Mott insulator to superfluid transition in the Bose-Hubbard model:A strong coupling approach[J].Phys Rev A,2005,71:Art 033629,8pp.

[18] 许莹,李晋斌.大粒子数二维硬核玻色子系统的量子蒙特卡罗模拟[J].物理学报,2012,61(11):61-69.

[19] 陈锟,邓友金.用量子蒙特卡罗方法研究二维超流-莫特绝缘体相变点附近的希格斯粒子[J].物理学报,2015,64(18):1-13.

[20] 周伟,周文慧,谢明轩.拓展Bose-Hubbard模型的有限系统密度矩阵重整化群算法[J].长沙理工大学学报:自然科学版,2015,12(2):78-82.

[21] 周文慧,王佳,符力平.玻色哈伯德模型的有限系统密度矩阵重整化群算法[J].量子光学学报,2011,17(4):284-288.

A Simple Method to Solve the Bose-Hubbard Model

ZHANGDanwei1,2

(1.School of Physics and Telecommunication Engineering,South China Normal University,Guangzhou 510006,China;2.Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials,Guangzhou 510006,China)

For the Bose-Hubbard model that describes many-body interacting boson system in lattices,the ground states of the system when the ratios between the interaction and hopping energies tend to infinity and zero limits are respectively calculated.The Mott insulator and superfluid phases in these two cases are respectively obtained.Secondly,based on the mean-field approximation and the second-order perturbation method with the order parameter for the superfluid states,the ground-state energy of the system is calculated and then the boundary equation of the quantum phase transition from the superfluid state to the insulating state is obtained.Finally,the phase diagram of the Bose-Hubbard model is obtained by solving the phase boundary equation by using numerical software.This mean-field method for solving the Bose-Hubbard model is not only able to obtain the complete phase diagram,but also able to provide the concise physical figure which is clear in the whole process and easy to understand.

Bose-Hubbard model; superfluid state; Mott insulator state; mean-field approximation; phase diagram

2016-05-24

广东省自然科学基金项目(2016A030313436)；广东省高校优秀青年创新人才培育项目(2015KQNCX023)

张丹伟(1986-)，男，广东潮州人，讲师，博士，主要从事超冷原子与凝聚态物理方面的研究，(E-mail)zdanwei@126.com

1673-1549(2016)04-0074-04

10.11863/j.suse.2016.04.16

O469

A