PMSM伺服系统速度环高阶模型实验建模及分析

潘海鸿，王 玲，陈 琳，林晓词，何蕴达

(1.广西大学，南宁 530004；2.广西制造系统与先进制造技术重点实验室，南宁 530004)



PMSM伺服系统速度环高阶模型实验建模及分析

潘海鸿1,2，王 玲1，陈 琳1,2，林晓词1，何蕴达1

(1.广西大学，南宁 530004；2.广西制造系统与先进制造技术重点实验室，南宁 530004)

针对PMSM伺服系统速度环理论建模过程中忽略系统参数时变、负载扰动、电机非线性和死区等因素导致建模不精确的问题，提出使用动态信号分析仪(DSA)获取PMSM伺服系统的高阶实验模型。通过搭建基于DSA的PMSM伺服系统速度环建模实验平台，获取PMSM伺服系统速度环的三阶、四阶和六阶数学模型；基于获取的不同阶次的模型进行PI参数整定，将整定结果输入到伺服驱动器中，并通过DSA测试伺服系统速度阶跃响应情况。实验结果表明：该实验建模方法可行、有效，可获得符合实际PMSM伺服系统速度环频率特性的数学模型，并可以应用于伺服系统设计、性能分析与参数整定。

PMSM伺服系统；速度环；建模；动态信号分析仪

0 引 言

PMSM伺服系统性能优良广泛应用于数控机床、工业机器人和航空航天等领域[1-2]。PMSM伺服系统速度环的主要作用是抑制负载扰动对系统的影响，从而减小速度波动[3-4]。而系统模型又是进行系统设计、性能分析与参数整定的基础，因此建立PMSM伺服系统速度环模型并基于模型整定其控制器参数，对提高整个系统的抗干扰能力有重要意义。

对PMSM伺服系统速度环建模的方法主要有理论建模和实验建模[5]两种,其中理论建模是指在被测对象运动规律的基础上，利用物理和化学定律以及数学原理，建立和描述系统输入、输出以及系统状态之间的关系。在理论建模时一般会忽略伺服系统中存在的非线性、死区、参数时变和负载扰动等因素，使得建立的模型与实际系统的动态响应有较大的差异[6-9]；实验建模是指对被测对象施加已知的输入信号激励被测对象，采集并处理输出信号，应用数学手段分析、确定系统输入与输出之间的关系。在实验建模时需要解决三个问题：辨识实验设计、数据预处理和辨识方法[10]。其中辨识方法是关键，传统的辨识方法主要有最小二乘法、辅助模型辨识法、梯度辨识法、多新息辨识法、极大似然辨识法、递阶辨识法和贝叶斯辨识法等[10-11]。针对不同用途对辨识方法进行修正和结合，又有递阶最小二乘法、多新息最小二乘法、递阶梯度迭代法等[10]。近年来，神经网络、遗传算法等智能算法与上述辨识方法相结合应用于系统辨识出现了许多新算法。这些算法普遍存在收敛性、收敛速度和辨识精度的问题，为提高辨识精度和收敛速度需要完善辨识算法，这样会使算法变得复杂[11-13]。

通过上述对比，本文采用实验建模的方式，提出通过DSA对PMSM伺服系统速度环的模型进行辨识。DSA设备能够用最小二乘法对系统频率特性曲线进行拟合来进行系统辨识，由于输入、输出信号可以准确获取，因此使用最小二乘法可以简便、准确地辨识未知参数，最后建立所需要的实验模型。基于获取的实验辨识模型，再对控制器PI参数进行整定，最后通过实验验证获取的实验建模可行、有效。

1 伺服系统速度环理论建模

建立PMSM伺服系统速度环数学模型是PMSM伺服系统速度环性能分析与参数整定的基础。PMSM伺服系统速度环主要包括电流闭环、伺服电机、以及反馈滤波等环节，将电流环等效为一阶惯性环节，分别对各个环节建模，可以建立如图1所示的模型[14]。其中Tv为前向滤波时间常数，Kvf为检测环节反馈系数，1/K是电流环等价的一阶惯性环节时间常数，Kt为转矩系数，Jm为电机轴转动惯量，B为电机阻尼系数。将图1模型转换为单位负反馈的形式，如图2所示。

图1 速度环简化控制框图

图2 速度环简化单位负反馈控制框图

2 伺服系统速度环实验建模

DSA可以用于转动机械测量、结构测量、声学测量、频谱和网络测量和控制系统测量[15]。本文使用DSA的控制系统测量功能。DSA内置波形信号源可以产生正弦扫频信号，用于测量被测环节Bode图；其具有的平均功能可以滤除测量过程中的测量噪声，使得测量结果真实、准确；其具有的曲线拟合和数学运算功能，可以由Bode图拟合获取被测环节的传递函数[15]。系统建模是分析系统性能和参数整定的基础，使用DSA建模首先需要测量获取伺服系统速度环的频率特性曲线；然后通过曲线拟合获取其数学模型。其中获取频率特性曲线主要有开环测量和闭环测量两种方式，其测量框图如图3所示。

两种测量方式都可获取被测系统以及被测系统被控对象传递函数[15]。设DSA测量结果为G，则系

(a)开环测量(b)闭环测量

图3 DSA测量频率特性曲线框图

统数学模型Gs和被控对象Gp在开环测量和闭环测量时可以由式(1)和式(2)分别计算获得。

(1)

(2)

3 实验与结果分析

3.1 实验平台

为了对PMSM伺服系统速度环实验建模，依据图3(b)设计图4的实验平台，该平台主要由伺服驱动部分、D/A转换电路和DSA三部分组成。伺服驱动部分为东元TSB08751C伺服电机(750 W)及驱动器，参数如表1所示；DSA为Agilent35670A，参数如表2所示;D/A转换电路采用16位串行数模转换芯片DAC714，时钟频率10 MHz。其中DSA输入通道CH1和CH2要求输入信号为模拟量，D/A转换电路用于将编码器速度信号转换为模拟电压。

图4 实验平台

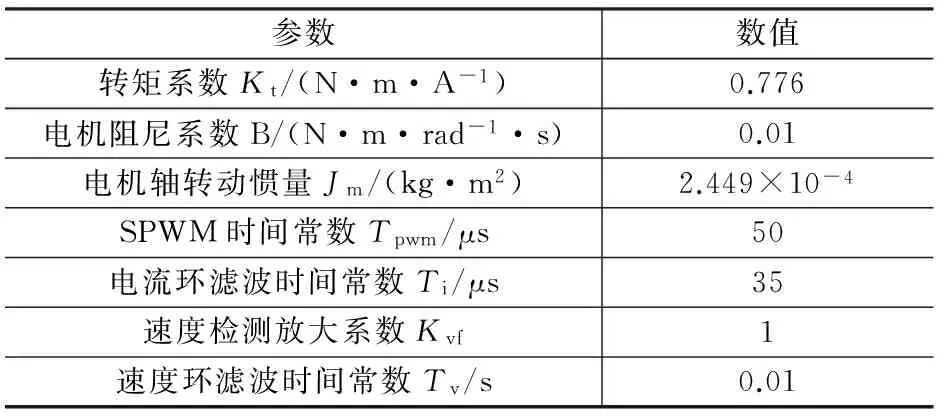
表1 TSB08751C伺服电机参数

表2 Agilent35670A主要参数

3.2 速度环理论建模与控制器PI参数整定

东元伺服系统速度环PI控制器的传递函数：

(3)

由图2可知，速度环被控对象的传递函数表达式：

(4)

将表1参数代入式(4)则速度环被控对象传递函数：

(5)

其中电流环简化一阶惯性环节时间常数1/K=2(Ti+Tpwm)[16]。基于理论建模使用MATLAB中的sisotool对速度环PI控制器参数进行整定[17]，以阶跃响应无超调、调节时间尽可能短为性能指标获取的整定结果如下：

(6)

由整定结果可知，PI控制器比例系数为0.017 Hz、积分时间常数为30.86 ms。东元TSB08751C伺服系统速度控制器比例参数调节范围为10～450 Hz，积分时间常数调节范围为0.2～100 ms。由此对比可知通过理论建模并进行PI参数整定，整定结果与实际驱动器参数不匹配，无法应用。

3.3 速度环实验建模与控制器PI参数整定

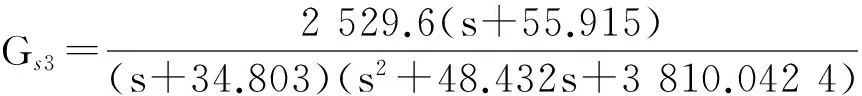
(7)

(8)

(9)

图5 伺服系统速度环闭环实际测量Bode图图6 伺服系统速度环闭环拟合Bode图

由图6对速度环闭环不同阶次Bode图拟合情况可知，拟合获取的三阶模型其幅频曲线在0.5～60 Hz范围内与系统实测的幅频曲线几乎重合，相频曲线在0.5～20 Hz范围内与实测相频曲线几乎重合。拟合获取的四阶模型其幅频曲线在0.5～100 Hz范围内与系统实测的幅频曲线几乎重合，相

频曲线在0.5～40 Hz范围内与实测相频曲线几乎重合。拟合获取的六阶模型其幅频曲线在0.5～150 Hz范围内与系统实测的幅频曲线几乎重合，相频曲线在0.5～150 Hz范围内与实测相频曲线几乎重合。可知三个不同阶次模型中六阶模型与PMSM伺服系统速度环实际频率特性最符合。

按照如图7所示的参数整定流程，依据阶跃响应无超调，调节时间尽可能短对速度环PI控制器参数进行整定，分别基于实验辨识的三阶、四阶和六阶模型，获得整定结果如表3所示。

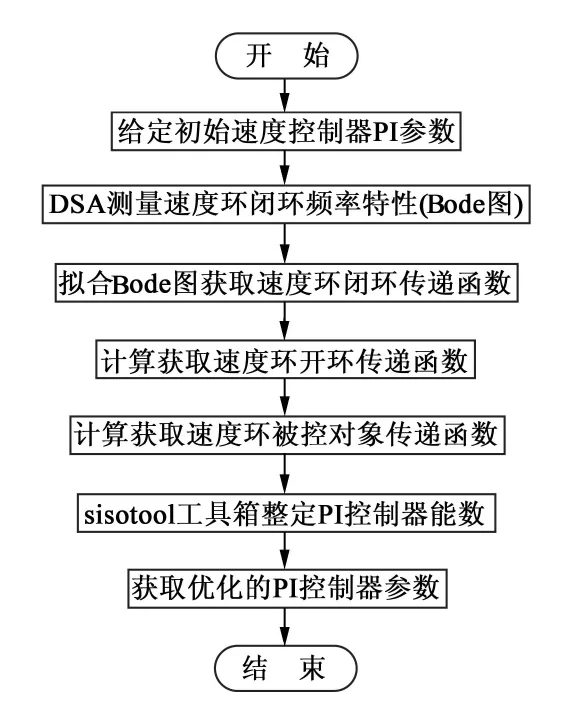
图7 基于实验建模整定速度控制器PI参数流程图

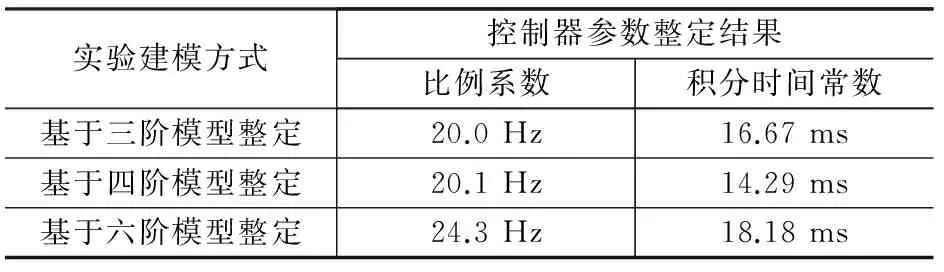
表3 伺服系统速度控制器PI参数整定结果

将整定结果输入至伺服驱动器中，伺服驱动器外部速度信号输入4 V(800 r/min)的阶跃信号，由DSA测量获取电机阶跃响应如图8所示。实验结果如下：(1)经过上述方法对速度控制器PI参数进行整定，整定结果可用于驱动器参数调节；(2)整定后系统的超调量减小，调整时间减少，系统性能提高；(3)基于六阶模型整定结果对应的阶跃响应超调量最小。

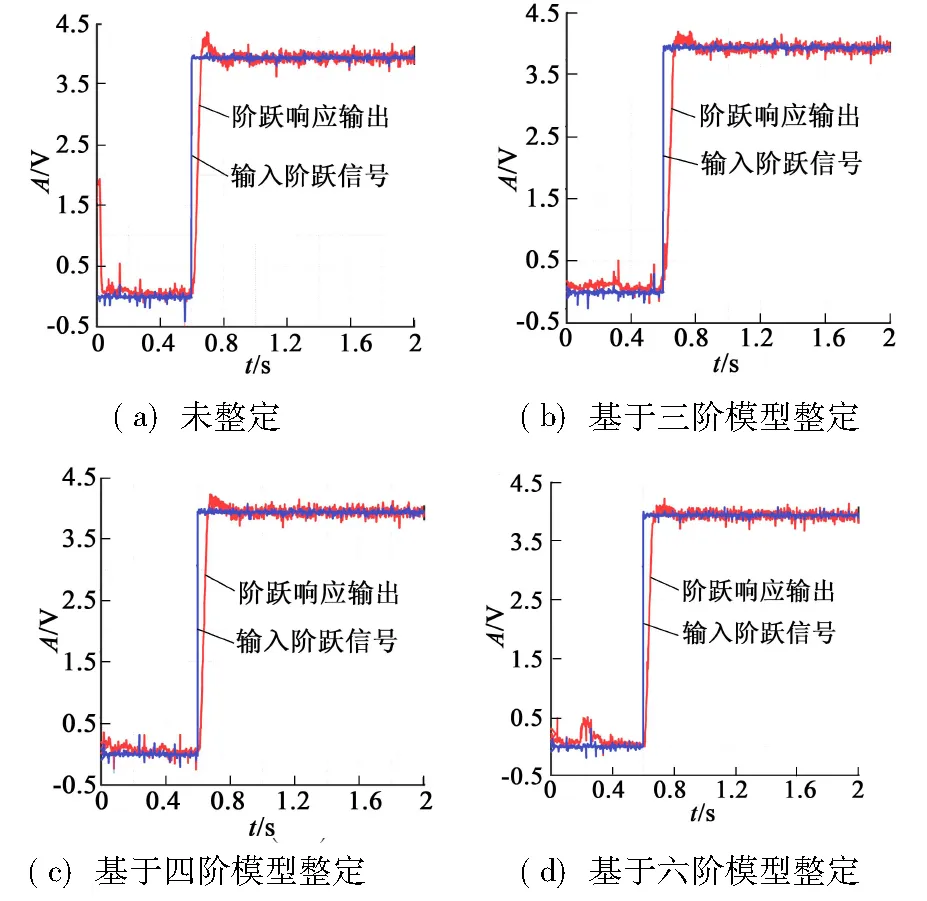
(a)未整定(b)基于三阶模型整定(c)基于四阶模型整定(d)基于六阶模型整定

图8 基于不同阶次模型PI参数整定后系统速度阶跃响应

由实验结果可知：(1)采用DSA实验建立伺服系统速度环模型是有效的；(2)基于实验建立模型整定速度控制器PI参数的方法是可行和有效的。但是由于测量过程中难免会存在误差，伺服系统速度环低阶模型存在一定的简化，且电机空载时易受外界干扰，因此按照性能指标要求整定的控制器PI参数并未使电机在实际运行中超调量减小到0，但性能有明显改善，说明该方法的有效性。

4 结 语

本文针对PMSM伺服系统速度环理论建模与实际系统动态响应有较大差异的问题，采用DSA实现对PMSM伺服系统速度环高阶模型的实验建模，通过拟合实际测量的速度环频率特性曲线来获得速度环更为精确的数学模型；并基于该实验模型整定速度控制器PI参数，最终获得了伺服驱动系统较高的速度响应性能。

[1] 朱中卫. 基于DSA的伺服系统速度环建模与PI参数整定[D].南宁：广西大学,2014.

[2] 吴春,齐蓉,李兵强,等.永磁同步电动机在电动舵机伺服系统中的应用[J]. 微特电机,2012,40(5):10-12.

[3] 李建军,桂卫华. PMSM交流伺服系统负载转矩动态补偿方法[J]. 微特电机,2007,35(5):16-19.

[4] 陈鹏展. 交流伺服系统控制参数自整定策略研究[D].武汉：华中科技大学,2010.

[5] 杨承志,孙棣华,张长胜. 系统辨识与自适应控制[M]. 重庆：重庆大学出版社,2003.

[6] 朱敏,于海生. 永磁同步电动机伺服控制系统哈密顿建模与仿真[J]. 微特电机,2007,35(2):4-7，17.

[7] 刘栋良,贺益康. 交流伺服系统逆变器死区效应分析与补偿新方法[J]. 中国电机工程学报,2008,28(21):46-50.

[8] Du H, Nair S S. Modeling and compensation of low-velocity friction with bounds[J].IEEE Transactions on Control Systems Technology,1999,7(1):110-121.

[9] 卢泽生,张强. 高精度交流伺服系统的模糊PID双模控制[J].北京航空航天大学学报,2007,33(3):315-318.

[10] 丁锋.系统辨识(1):辨识导引[J].南京信息工程大学学报：自然科学版,2011,3(1):1-22.

[11] 王琳,马平.系统辨识方法综述[J].电力情报,2001,(4):63-66.

[12] 王清太,段毅. 神经网络在某交流伺服系统建模中的应用[J].火力与指挥控制,2008,33(11):152-154.

[13] 刘通,童仲志. 基于RBF神经网络的某交流伺服系统辨识研究[J].机械制造与自动化,2013,42(2):113-115.

[14] 肖启明,杨明,刘可述,等.PMSM伺服系统速度环PI控制器参数自整定及优化[J]. 电机与控制学报,2014,18(2):102-107.

[15] Agilent company.Agilent 35670A Operator's Guide[M].Agilent Technologies,2010.

[16] 阮毅,陈伯时. 电力拖动与自动控制系统——运动控制系统[M]. 4版. 北京：机械工业出版社, 2013.

[17] 李钟慎. 用sisotool实现经典控制系统的设计与仿真[J]. 计算机仿真,2007,24(5):173-175.

Experimental Modeling and Analysis of High Order Model for Speed Loop in PMSM Servo System

PANHai-hong1,2,WANGLing1,CHENLin1,2,LINXiao-ci1,HEYun-da1

(1.Guangxi University,Nanning 530004,China;2.Guangxi Key Laboratory of Manufacturing System & Advanced Manufacturing Technology,Nanning 530004,China)

Mechanism modeling is used to model the speed loop of PMSM servo system in general. However, the system model is inaccurate in this method, because of some factors neglected. These factors mainly include time-varying characteristic of system parameters, load disturbance, nonlinearities and dead time of motor, etc. In this paper, a experimental method, modeling based on dynamic signal analyzer (DSA), was proposed. To establish the speed loop model of PMSM servo system, the experimental platform based on DSA was built, then the three-order, four-order and six-order mathematical models of speed loop were obtained. According to these mathematical models the PI parameters of speed controller were adjusted. Then the results of parameter tuning were input into servo driver. In final the speed step response was measured by DSA to evaluate the performance of system. Experimental results demonstrate that the presented method is feasible and effective. By the DSA-based experimental modeling method, the established mathematical model conforms to the frequency response characteristic of speed loop in PMSM servo system, and it can be applied to the design, performance analysis and parameters tuning of the servo system.

PMSM servo system; speed loop; modeling; dynamic signal analyzer

2015-06-22

国家自然科学基金项目(51465005)；广西制造系统与先进制造技术重点实验室项目(14-045-15S09)

TM341;TM351

A

1004-7018(2016)04-0052-04

潘海鸿(1966-)，博士,教授，研究方向为高速高精度运动控制、数控技术。