基于定子磁链定向的异步电动机准比例谐振控制

张 琦，纪同快

(中国矿业大学，徐州 221116)



基于定子磁链定向的异步电动机准比例谐振控制

张 琦，纪同快

(中国矿业大学，徐州 221116)

针对直接转矩控制和转子磁链定向控制的不足，从异步电动机的数学模型分析出发，提出了一种新型的异步电动机按定子磁链定向的控制方法；同时，系统引入了准比例谐振控制器(QPR)，它克服了PI控制器的缺点，能够在静止坐标系下无静差的跟踪交流信号；经过MATLAB/Simulink仿真验证，在该控制方法下，电机转矩脉动小、定子电流谐波含量少，系统具有良好的动态性能。

异步电动机；定子磁链定向；准比例谐振控制

0 引 言

基于转子磁链定向的PI 控制和直接转矩控制在异步电动机调速系统中应用十分广泛，这两类系统各有其优缺点。

异步电动机基于转子磁链定向的PI控制方法存在解耦问题，并且其解耦性能的好坏与转子磁链观测器的准确与否密切相关，而转子磁链的计算公式中含有易于变化的转子电阻，这导致了转子磁链的估算受电机参数的影响巨大[1]。同时PI控制器只对直流量有良好的跟踪效果，而且需要复杂的坐标变换和前馈解耦，在补偿精度、采样速度和鲁棒性方面存在不足[2]。

直接转矩控制采用砰砰控制，优点在于控制系统结构简单，受电机参数影响小，容易数字化。但这种不连续的控制造成了低速开关频率低、开关频率不固定、转矩脉动大等缺点[3]。

文献[4]提出了一种新型的基于定子磁链定向的控制方法，其控制方式是对磁链环进行定子电阻压降补偿，对转矩环与电流环进行闭环连续控制。该方法的优点是避免了转子电阻对控制系统造成的影响，不足之处是仍采用PI控制，无法避免PI控制器的缺点。

准PR控制器具有对谐振频率信号增益大，其他频率信号衰减大的特点，将其引入电机控制系统中可以在静止坐标系下实现对特定频率信号无稳态误差跟踪，同时免去了解耦问题，但其一般应用在永磁同步电机中[5-6]，异步电动机中应用很少，究其原因是异步电动机的基频是一个变量。

本文在分析了上述控制方法的基础上，提出了一种新型的基于定子磁链定向的异步电动机准PR控制方法。该方法的优势在于：按定子磁场定向避免了磁链计算受转子电阻的影响；采用了连续的控制方法以及电压空间矢量PWM控制技术的应用，克服了砰砰控制造成的转矩脉动并且具有固定的开关频率；采用准PR控制克服了系统存在的稳态误差，实现交流无静差控制[5]。

1 异步电动机定子磁链定向控制原理分析

1.1 异步电动机按定子磁链定向的数学模型

在以A相定子轴线为参考矢量的旋转坐标系下，取定子磁链[ΨsdΨsq]T、定子电流[isdisq]T和转速ω为状态变量，并建立异步电动机数学模型[4,7]。

(1)

在定子磁链定向下，定子电流可正交分解成直轴电流isd表示励磁分量和交轴电流isq表示转矩分量。由式(1)可导出：

(2)

稳态时：

(3)

式(2)和式(3)表明，在定子磁链定向下，磁链Ψsd的产生与isd和isq都有关系，并且只要电磁转矩存在，isq就会削弱磁场。所以，采用isd来控制定子磁链会使控制系统存在严重的交叉耦合。因此本文采用定子电阻压降补偿法，利用直轴电势控制磁链；采用旋转电动势补偿法，利用交轴电势控制转矩，这样既避免了采用isd控制带来的耦合问题，又是实现了励磁与转矩的连续控制，并降低了电机参数对系统的影响。

1.2 定子磁链控制

由式(1)得直轴电势控制方程如下：

(4)

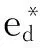
(5)

定子磁链在两相静止坐标系的两个分量计算公式如下：

(6)

对式(6)两个分量进行极坐标变换可得定子磁链幅值和角度。

(7)

1.3 电磁转矩控制

电磁转矩的计算公式如下：

(8)

式中:p为电机极对数，将式(8)进行变换可得isq的计算公式如下：

(9)

将式(9)代入式(1)的第二式得：

(10)

(11)

式中：k=1.5Rs/pΨsd是一个常数，可将其并入转速控制器中。

2 基于准PR控制器的异步电动机定子磁链定向控制

2.1 准PR控制器的特性

准PR控制器既继承了PR控制器对特定频率信号增益大的优点，又避免了高增益频带过窄导致系统对输入频率参数敏感过度的缺点。准PR控制器传递函数如下[5-6,8]：

(12)

将s=jω代入式(12)中可以求出在基波频率处的增益：

(13)

从式(12)中可看出，准PR控制器对基波的增益可通过调整参数来调节，避免了PR控制器在基频处增益无穷大而造成的稳定性问题[4]。

准PR控制器的参数有三个分别是Kp,Kr,ωc，通过单一变量原则探究这三个变量对准PR控制器的影响。为方便分析假定ω0=100rad/s并绘制准PR控制器的Bode图,如图1所示。

从图1中可以看出，参数ωc影响系统的带宽，ωc越大带宽越大；参数Kp对基频信号影响不大,但对低频与高频信号的幅值增益与相位裕度影响较大，降低Kp的值则低频与高频信号的幅值增益也会减少，但Kp不能过小，否则系统的动态响应会降低；参数Kr影响了系统基波峰值增益，Kr越大基波峰值增益越大。所以在选择参数时，选取较大的Kr值保证基频处有较大的增益；选取较大的ωc值增大系统的带宽，降低系统的敏感度，但ωc值不能过大，否则会降低系统的选频性能，根据工程经验，一般取ωc的值小于20。

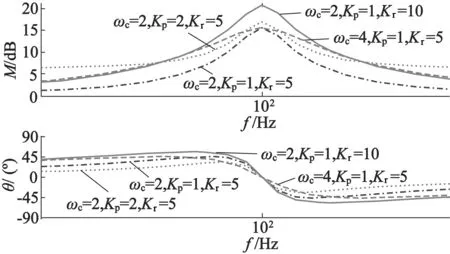
图1 Kp，Kr，ωc取值不同时准PR控制器的bode图

2.2 基于双二阶广义积分器的自适应锁频环

准PR控制器正常工作的前提是要知道基频ω0，而异步电动机电压的基频是一个随转矩和转速变化而变化的量，因此需要一个能自适应频率变化的锁频环，而文献[9-11]中提出的基于双二阶广义积分器的锁频环(DSOGI_FLL)正好满足要求，图2为DSOGI_FLL结构框图。

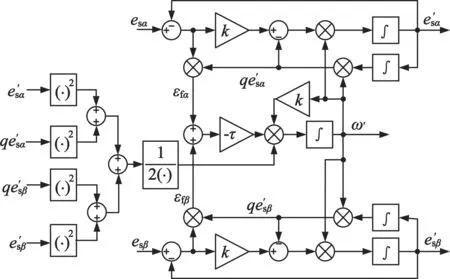
图2 DSOGI_FLL结构框图

通过对图2系统分析，可以得到SOGI_FLL的频率响应近似表达式：

(14)

式中:ω为输入信号的频率;ω′为锁频环锁定的频率。从式(14)可以看出,DSOGI_FLL可以简化成一个时间常数为1/(2τ)惯性环节，因此其锁定的频率所需的时间不会因为输入量的幅值和频率的变化而变化。将DSOGI_FLL的输出量送到准PR控制器中保证其正常工作。

2.3 异步电动机控制系统框图

基于上述分析，图3给出了异步电动机基于定子磁链定向的准PR控制的控制框图。

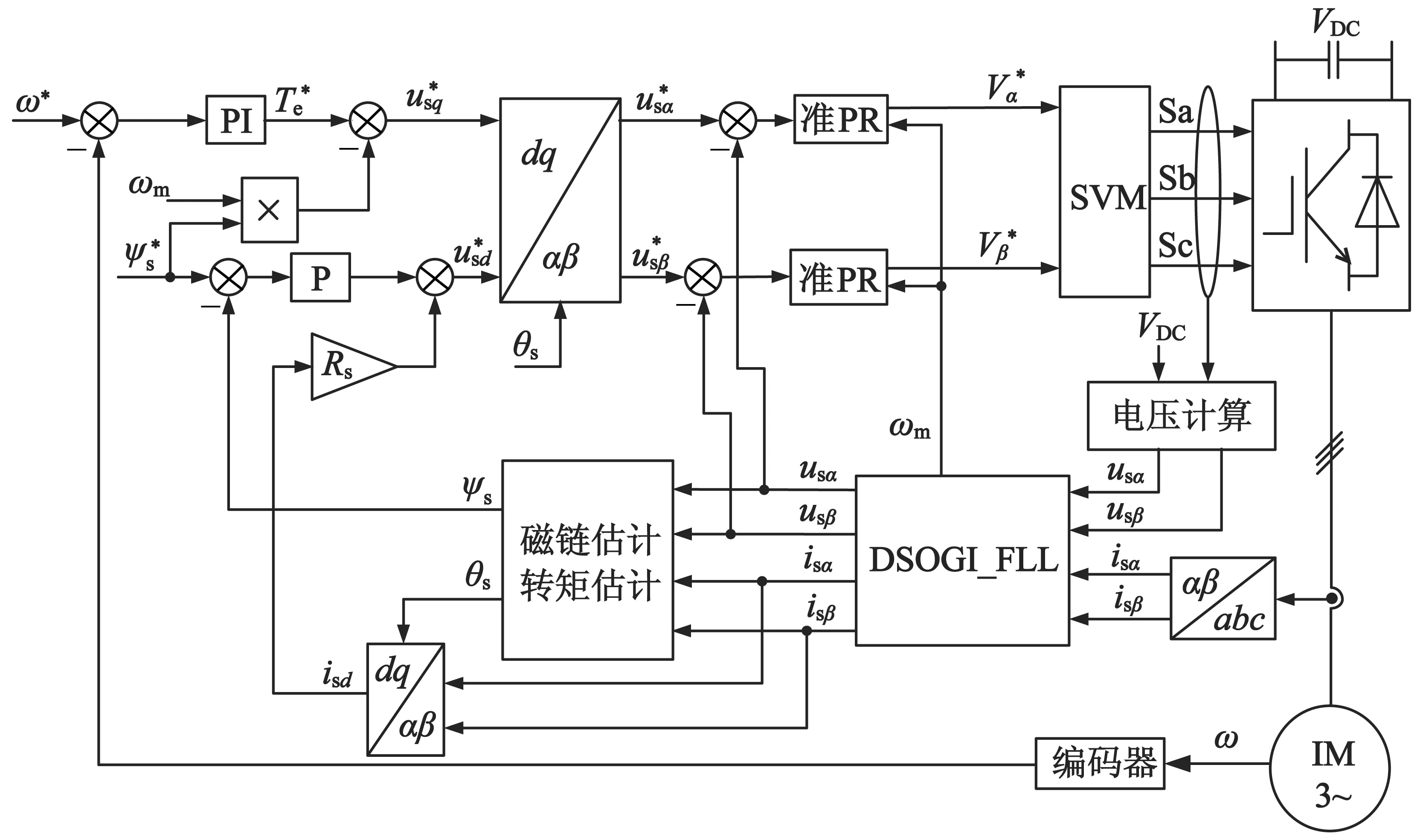
图3 异步电动机基于定子磁链定向的准PR控制的控制框图

3 仿真验证

图4 电机转速波形

从图4可以看出，电机加速平稳，超调量小；在0.4 s转速突变时，电机也能迅速响应，动态性能好；在0.7 s转矩增加时，转速无变化，抗干扰能力强，稳态时转速脉动微小。从图5(a)可看出，稳态时定子磁链脉动小，不存在直流偏置与原点漂移误差。从图5(b)、图5(c)、图5(d)可看出，异步电动机定子电流波形是正弦的，谐波含量低。从图6可看出，电机转矩响应迅速，稳态时转矩脉动小。从图7可看出，DSOGI_FLL能够迅速准确地锁定异步电动机的基波频率。

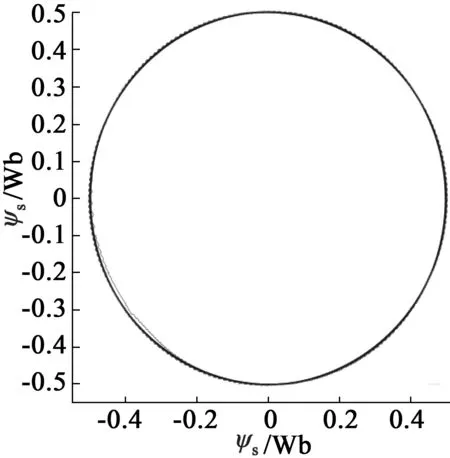
(a) 定子磁链圆

(b) 电机转速为500 r/min时A相定子电流波形与FFT分析

(c) 电机转速为900 r/min时A相定子电流波形与FFT分析

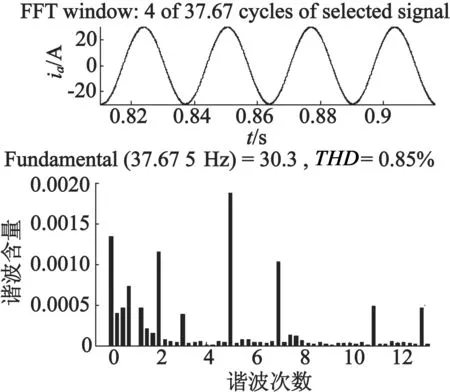
(d) 转矩增加时A相定子电流波形与FFT分析

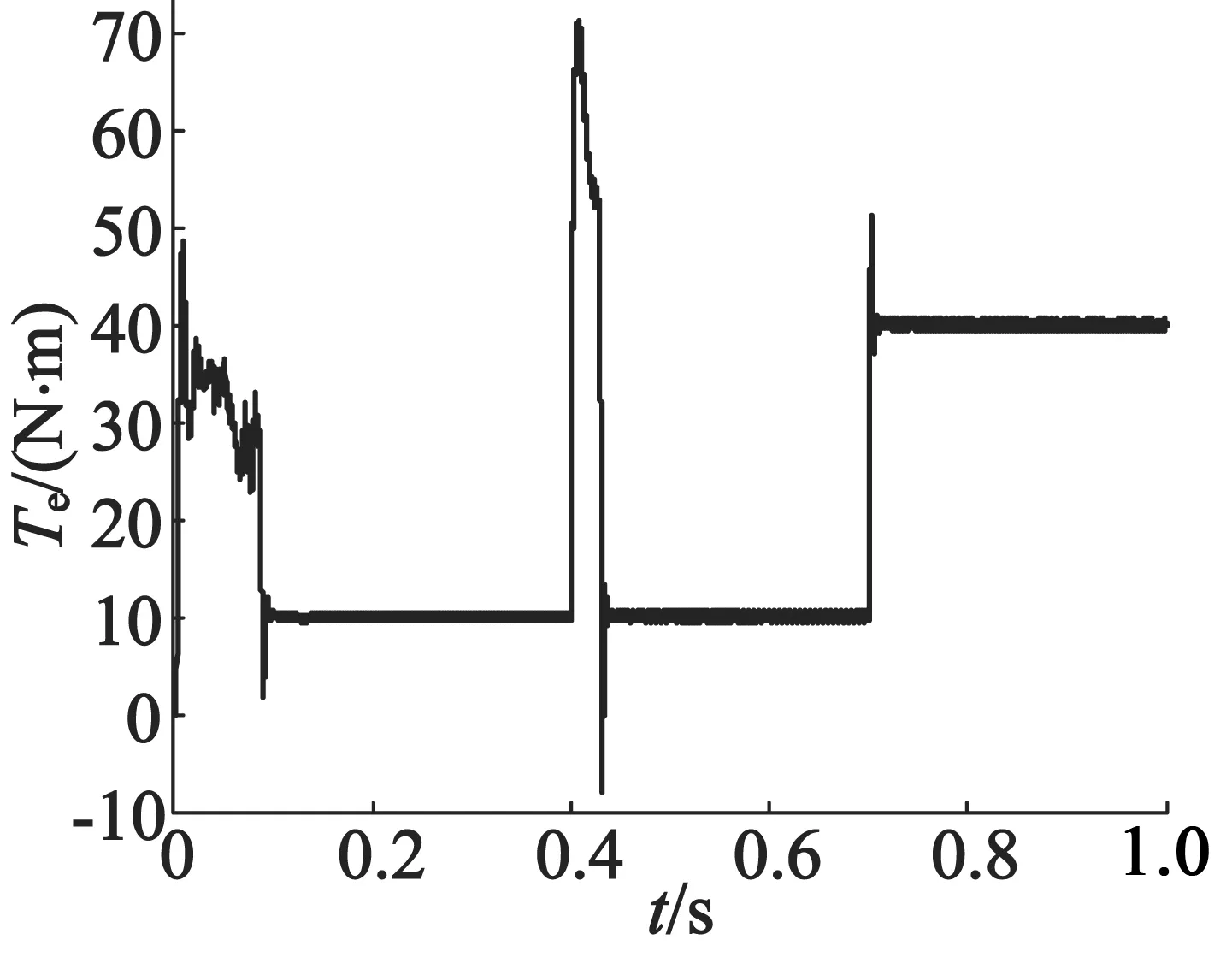
图6 电磁转矩波形

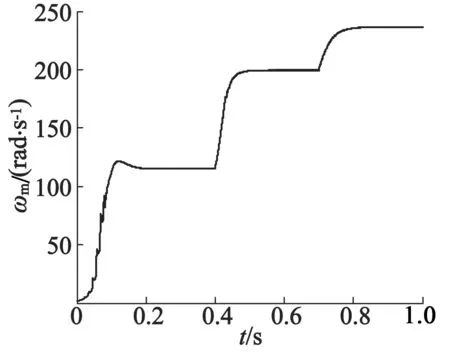
图7 DSOGI_FLL锁频波形

4 结 论

1)基于定子磁链定向的异步电动机准PR控制方法避免易于变化的转子电阻对系统造成的影响，准PR控制使得系统不存在解耦的问题，简化了控制系统。

2)仿真结果表明,系统具有良好的动静态性能，定子电流谐波含量少，转矩脉动小。

3)本文提出的控制方法为异步电动机准PR控制提供了一种思路，为后续更深入的研究打下基础。

[1] 陈世浩，冯晓云，李官军，等.基于转子磁链定向的异步电动机矢量控制仿真研究[J].电气技术，2008,3(1):44-45.

[2] 申科，王建赜.动态电压恢复器比例谐振控制[J].电力自动化设备,2010,30(7): 65-68.

[3] SIVANANTHAM R,SIVAPRAKASAM A.Direct torque control for induction motor using 12-sector methodology[C]//National Conference on Trends in Power System,Power Electronics and Drives (PSPED 2010),SSN College of Engineering, Chennai,2010:33-38.

[4] 阮毅，张晓华，徐峰，等.感应电动机定子磁链定向控制[J].电工技术学报,2003,18(2):1-4.

[5] 邓超，黄守道，李中启，等.基于比例谐振的 PMSM-SVM-DTC系统[J].电工技术学报,2013, 28(1):501-507.

[6] 严伟，周腊吾，浦清云，等.基于PR控制的永磁同步电动机弱磁控制[J].微特电机，2011,39(3)：42-44.

[7] 陈伯时.电力拖动自动控制系统[M].3版.北京：机械工业出版社，2003.

[8] 雷亚雄，李建文，李永刚.基于准PR调节器双闭环LCL三相并网逆变器控制[J].电力系统保护与控制，2014,42(12):44-50.

[9] 辛振，赵仁德.基于双二阶广义积分器-锁频环的异步电机同步角频率估计方法[J].中国电机工程学报，2014,34(27):4676-4682.[10] WANG Gaolin,DING Li.Enhanced position observer using second-order generalized integrator for sensorless interior permanent magnet synchronous motor drives[J].IEEE Transactions on Energy Conversion,2014,29(2):486-495.

[11] CIOBOTARU M,TEODORESCU R,BLAABJERG F.A new single-phase PLL structure based on second order generalized integrator[C]//Power Electronics Specialists Conference,2006:1-6.

Quasi-Proportional-Resonant Control of Induction Motor Based on Stator Flux Orientated

ZHANGQi，JITong-kuai

(China University of Mining and Technology,Xuzhou 221116，China)

For the shortcoming of direct torque control and rotor flux orientation control, a novel control strategy of induction motor with stator flux orientation was presented in this paper, proceeding from the analysis of the mathematical model of induction motor. Meanwhile, quasi-proportional-resonant(QPR) was introduced into the control system, which overcomes the deficiency of the PI and can realize no static error adjustment tracking the AC signal in the stationary coordinate system. Proved through the simulation using MATLAB/Simulink, the program can maintain a fast dynamic response characteristics as well as a little torque ripple, but also a little harmonic in stator current.

induction motor; stator flux orientation; quasi-proportional-resonant control

2015-09-07

TM343

A

1004-7018(2016)04-0043-04

张琦(1988-)，男，硕士研究生，研究方向为电机控制、电力电子等。