基于分数低阶谱图的非平稳信号时延估计

孙永梅，邱天爽，王富章，郭宇明

(1.中国铁道科学研究院 电子计算技术研究所，北京 100081； 2.大连理工大学 电子信息与电气工程学部，辽宁 大连 116024； 3.大连交通大学 图书馆，辽宁 大连 116028)



基于分数低阶谱图的非平稳信号时延估计

孙永梅1，邱天爽2，王富章1，郭宇明3

(1.中国铁道科学研究院 电子计算技术研究所，北京 100081； 2.大连理工大学 电子信息与电气工程学部，辽宁 大连 116024； 3.大连交通大学 图书馆，辽宁 大连 116028)

依据分数低阶统计量理论，讨论了分数低阶短时Fourier变换、分数低阶谱图等时频表示方法在非高斯FLOA噪声环境下的适用性.针对传统时间延迟估计方法在非高斯非平稳环境下的退化现象，提出一种基于分数低阶谱图的非平稳信号时间延迟估计新方法.理论分析和仿真实验结果表明，新方法同时适用于高斯和非高斯FLOA噪声环境下的非平稳信号时间延迟估计，具有良好的韧性.

时间延迟；非平稳；分数低阶；谱图

0 引言

时间延迟估计是信号处理领域中的重要研究内容，广泛应用于地球探测、生物医学、超声测距、被动定位、地震、雷达和声呐信号处理等领域.在上述各种应用中，对所研究信号和噪声特性和模型的不同描述，对于相应的时间延迟估计方法的性能具有十分重要的影响.实际应用中所遇到的信号多属于非平稳信号，附加噪声也常常不满足高斯分布[1- 3].因此，针对非高斯噪声环境下的非平稳信号的时间延迟估计问题成为亟待解决的研究课题.非平稳信号处理的一个常用的方法就是对信号进行时频分析，通过时间和频率的联合函数来表示非平稳信号，并对其进行分析和处理.将时频分析理论引入时间延迟估计方法是解决非平稳信号时延估计问题的一个有价值的研究方向.但是，当接收信号的附加噪声为非高斯Alpha稳定分布噪声时，上述的基于常规时频分析的时间延迟估计方法的性能退化，需要研究新的时间延迟估计方法.

1 分数低阶时频表示

1.1 短时Fourier变换

传统Fourier分析是将时域信号转换到频率域中，通过信号的频谱特性对其进行分析.但是Fourier变换反映的是全部时间范围内的频率特征，缺少这些频率在何时出现的信息.短时Fourier变换是非平稳信号分析中最基本的方法，它在Fourier变换的基础上，将非平稳信号看作是一系列短时平稳信号的叠加，通过时域加窗和平移参数来实现所谓的短时性和对整个时域的覆盖.短时Fourier变换(STFT)的变换公式如式(1)所示.

(1)

也就是对窗函数与非平稳信号的乘积进行Fourier变换.由STFT建立起来的频谱图可以反映出一段时间内的频率特性，但只要窗口大小确定了，其分辨率也随之确定[4- 5].

以STFT的模平方作为一种时频表示方式，称为谱图：

(2)

它是实值、非负的二次型分布，具有时移和频移不变性.

1.2 分数低阶短时Fourier变换

在实际应用中，很多非高斯信号或噪声往往具有显著的尖峰脉冲特性，其概率密度函数也会明显地偏离高斯分布模型.依据高斯假定所设计的信号处理算法在这种情况下会明显退化甚至不能正常工作.研究表明，Alpha稳定分布模型可以用于这类信号噪声的建模[6].所谓Alpha稳定分布是一种广义的高斯分布，信号脉冲特性的强弱由特征指数α∈(0,2]来描述，α值越小，其脉冲特性越强.当α=2时，Alpha稳定分布的表达式与高斯分布一致，也就是说，高斯分布是Alpha稳定分布的一种特殊情况.因此，Alpha稳定分布相比于高斯分布具有更加广泛的适用性，通常称0<α<2的情况为分数低阶Alpha稳定分布(FLOA)[6].

针对FLOA信号的尖峰脉冲特性，采用分数低阶统计量的信号处理方法，对原定义式中的信号项进行p阶矩运算，然后再对其进行加窗和Fourier变换，得到分数低阶短时Fourier变换(简称FLOSTFT)如下：

(3)

FLOSTFT作为一种非高斯非平稳信号的时频分析表示方法，可以有效地抑制附加噪声的尖峰脉冲特性，同时反映信号的时频分布特征.

1.3 分数低阶谱图

以FLOSTFT的模平方作为分数低阶时频表示，称为分数低阶谱图：

(4)

分数低阶谱图也是一种适用于非高斯非平稳信号的时频表示方法，其特点是减少了交叉项干扰，但同时降低了时频的分辨率.

2 基于分数低阶谱图的时间延迟估计

2.1 时间延迟估计模型

时间延迟估计系统的基本模型为双基元模型，设两个接收器A和B接收到的信号分别为x1(t)和x2(t)，则时间延迟估计问题的基本信号模型为

(5)

其中,s(t)为源信号，D为时延，λ为衰减系数.v1(t)和v2(t)分别为附加噪声.本文的分析和讨论中，假定s(t)为非平稳信号，v1(t)和v2(t)为非高斯FLOA噪声.

2.2 基于分数低阶谱图的时间延迟估计方法

对传感器接收的信号x1(t)和x2(t), 分别作分数低阶短时Fourier变换,得到FLOSTFTx1(t,ω)和FLOSTFTx2(t,ω)，定义分数低阶谱图的瞬时频域相关函数为:

(6)

式(6)是分数低阶谱图在频域的一维相关，取不同τ值计算频域相关系数R(t,τ).依据信号自相关特性，当τ=D时，R(t,τ)取得最大值，频域相关的信号能量最集中.因此，基于分数低阶谱图的时延估计方法就是寻找在瞬时频域相关的最大值，即：

(7)

3 计算机仿真

3.1 线性调频信号的仿真结果

(1)短时Fourier变换和分数低阶短时Fourier变换的比较

仿真信号采用线性调频(LFM)信号，初始归一化频率为0.1，终止归一化频率为0.3，长度N=256，附加为FLOA噪声，α=0.7，SNR=0 dB，参数P=0.1.图1为纯净LFM信号和含有Alpha稳定分布噪声的LFM信号的时域波形.利用STFT分别对纯净LFM信号和含有FLOA噪声的LFM信号进行变换，结果如图2所示.可以看出：对于纯净LFM信号，STFT能够很好地反映其时频分布，而对于含有FLOA噪声的LFM信号，STFT的性能变差.图3是利用FLOSTFT对两个LFM信号进行变换的结果.可以看出，无论是否含有噪声，FLOSTFT均具有良好的性能，适用于FLOA噪声下非平稳信号的线性时频分析.

(a)纯净LFM信号

(b)含噪LFM信号

(a)纯净LFM信号的STFT

(b)含噪LFM信号的STFT

(a)纯净LFM信号的FLOSTFT

(b)含噪LFM信号的FLOSTFT

(a)纯净LFM信号的谱图

(b)含噪LFM信号的谱图

(a)纯净LFM信号的分数低阶谱图

(b)含噪LFM信号的分数低阶谱图

(2)谱图和分数低阶谱图的比较

仿真条件同(1).图4和图5是分别利用谱图和分数低阶谱图对纯净LFM信号和含有FLOA噪声的LFM信号进行变换的结果.可以看出对于纯净LFM信号，谱图能够很好地反映其时频分布，而对于含有Alpha稳定分布噪声的LFM信号，谱图的性能变差. 但是分数低阶谱图能够有效抑制脉冲噪声，很好地反映LFM信号的时频分布.3.2 基于分数低阶谱图的时间延迟估计仿真

为了检验本文提出的时间延迟估计算法在FLOA环境下的韧性，按照式(5)构造两路输入信号，其中信号项为调幅-调频信号，时间延迟设定为D=10，信噪比设定为-5 dB.

图6和图7分别为不同噪声环境下利用谱图瞬时频域相关法和分数低阶谱图瞬时频域相关法估计时间延迟的结果.可以看出，在高斯环境下，信号x1(n)和x2(n)的谱图瞬时频域相关具有明显的单峰，可以由峰值对应的时刻得到正确的时间延迟估值.而在非高斯FLOA环境下，谱图瞬时频域相关受到脉冲噪声的影响，时间延迟估计出现伪峰，性能显著变差. 但是分数低阶谱图瞬时频域相关能够很好地抑制脉冲噪声，具有和高斯环境下同样的性能，可以由相关的峰值对应得到正确的时间延迟估值.

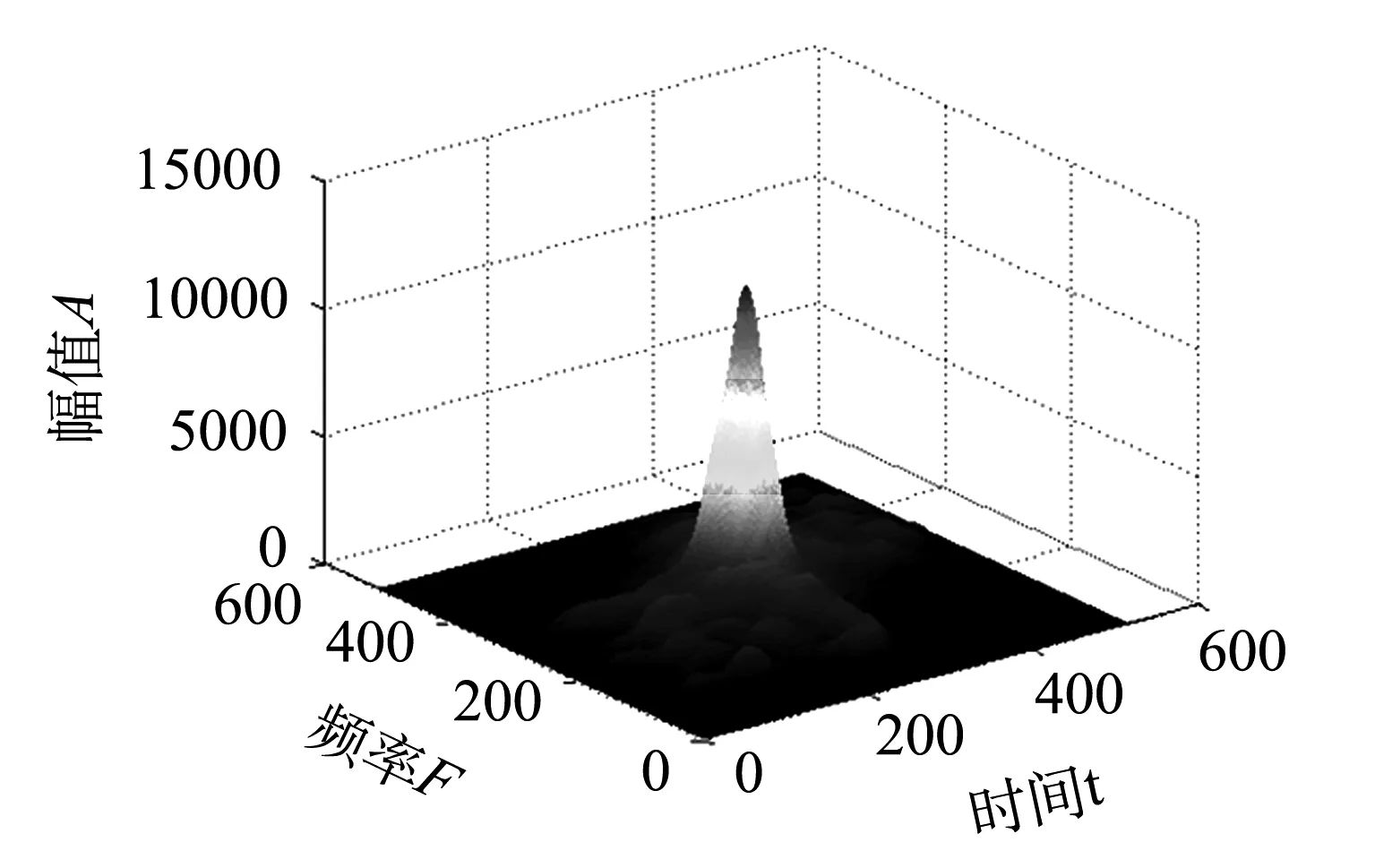
(a)附加高斯噪声

(b)附加FLOA噪声

(a)附加高斯噪声

(b)附加FLOA噪声

4 结论

本文针对传统时频分析方法和时间延迟估计方法在非高斯FLOA噪声环境下的退化现象，研究适用于这类噪声的时频表示方法，包括分数低阶短时傅里叶变换和分数低阶谱图，并在此基础上提出一种新的时延估计算法.理论分析和计算机仿真表明本文讨论的分数低阶时频表示方法适用于FLOA噪声下信号的时频表示，基于分数低阶谱图的时间延迟估计方法能够很好地抑制尖峰脉冲噪声，具有良好的韧性，适用于高斯和非高斯噪声环境.

[1]NAVIA A,ARENAS J.Combination of recursive least p-norm algorithms for robust adaptive filtering in alpha-stable noise[J].IEEE Trans.On Signal Processing,2012,60(3):1478- 1482.

[2]YANG Y,PENG Z,DONG X,et al.General parameterized time-frequency transform[J].IEEE Transactions on Signal Processing,2014,62(11):2751- 2764.

[3]严侃，雷江涛.基于时频分析的水声目标被动检测模型研究[J].2015，23(1)：26- 29.

[4]冯爱玲.基于短时傅里叶变换的胎心率检测算法与实现[D].柳州：广西工业大学，2014.

[5]DUAN Y,WANG Y J,SU S.Detection of LFM signals in low SNR based on STFT and wavelet de-noising：International conference on audio,language and image processing[C].2014.

[6]吴华佳.稳定分布下时频分析与循环统计量研究与应用[D].大连：大连理工大学，2009.

Time Delay Estimation Method of Non-Stationary Signals based on Fractional Lower Order Spectrogram

SUN Yongmei1,QIU Tianshuang2,WANG Fuzhang1,GUO Yuming3

(1.Institute of Computer Technologies,China Academy of Railway Sciences,Beijing 100081,China; 2.Faculty of Electronic and Electrical Engineering,Dalian University of Technology,Dalian 116024,China; 3.Library,Dalian Jiaotong University,Dalian 116028,China)

According to fractional lower order statistics theory,the applicability of fractional lower order short time Fourier transform and fractional lower order spectrogram under and non-Gaussian FLOA conditions is discussed.In order to combat the degeneration of traditional time delay estimation method under non-Gaussian and non-stationary environment,a new time delay estimation method based on fractional lower order spectrogram is proposed.Theoretical analysis and computer simulations indicate that the new time delay estimation algorithm is suitable for both Gaussian and non-Gaussian conditions.

time delay；non-stationary；fractional lower order；spectrogram

1673- 9590(2016)03- 0112- 05

2016- 01- 06

中国博士后科学基金资助项目(20070410347)

孙永梅(1974-)，女，副教授，博士，主要从事信号与信息处理方面研究E-mail:sunym1118@sina.com.

A