基于改进算子和空间矩的亚像素边缘检测方法

魏希扬，张旭秀

(大连交通大学 电气信息学院，辽宁 大连 116028)



基于改进算子和空间矩的亚像素边缘检测方法

魏希扬，张旭秀

(大连交通大学 电气信息学院，辽宁 大连 116028)

在Sobel算子基础上，给出了一个新的梯度算子，使用该梯度算子检测出边缘，再利用边缘位置信息对原图像使用空间矩进行检测，从而确定边缘的亚像素位置.同时，将其与Sobel算子的检测结果进行了对比.结果显示，在相同的检测条件下，新算子能够检测出更多的边缘.

Sobel算子；空间矩；亚像素；边缘检测

0 引言

边缘是图像的重要特征之一，是图像灰度值的不连续点或变化剧烈的点的集合.正确提取图像边缘能够减少图像处理的信息量，为进一步分析图像提供了方便[1].传统的检测算子如Sobel算子、Roberts算子、Prewitt算子等运算量小，操作简单，而在微分算子基础上发展起来的Canny算子具有较好的抗噪性.近年来，随着小波热以及一些特定理论学科的兴起,很多学者围绕边缘检测的问题，展开了大量的工作，提出了一系列新的边缘检测方法，如基于小波变换的边缘检测算法[2- 3]、基于数学形态学的边缘检测算法[4- 5]、基于模糊理论的图像边缘检测技术[6]以及基于神经网络学的检测技术[7]等.以上算法检测出的边缘，其检测精度最高只能达到一个像素远远不能满足实际需要，因此需要更高的检测精度，即亚像素级精度.为了达到亚像素精度，专家们陆续提出了许多不同原理的亚像素算法，这些方法大多可归为三类，即插值法[8- 9]、矩保持法[10- 11]以及拟合法[12- 13].

为了减少运行时间，通常会首先对边缘进行像素级检测，再对其进行亚像素级精确，这就使得像素级检测结果会对亚像素定位有直接影响.Sobel算子检测出的边缘光滑，连续，但容易丢失边缘，直接影响了之后的精确定位.本文提出了一个改进的算子，使其在相同的边缘判定条件下，比Sobel算子检测出的边缘更全面.

1 像素边缘提取

1.1 梯度算子推导方法

假设图像I在像素点(x,y)处的梯度是(a,b)，那么该点处的像素灰度值满足关系式：

(1)

那么每个像素及其周围8个像素值可以由以下矩阵表示：

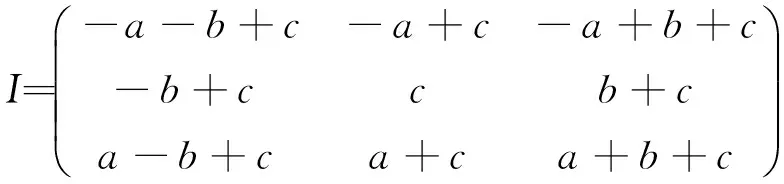
(2)

将水平和垂直算子分别定义为：

(3)

使用这两个模板同原始图像的像素进行卷积可以得到方向导数，也即对图像水平方向和垂直方向进行卷积运算后所得的响应：

(4)

由此可以得到像素梯度为：

(5)

式(5)中，若要使梯度g为常量，则应该使2(2m+n)=1.

取m=1/8，n=1/4时，等式成立，可以得到水平和垂直算子分别为：

(6)

由此可以得到Sobel算子包含的两个模板，如下所示：

(7)

Sobel算子是常用于图像处理和计算机视觉领域的一种重要处理方法，它包含如式(7)所示的两个3×3的矩阵模板，一个用于在水平方向上的运算，检测图像的垂直边缘，另一个用于垂直方向的运算，检测水平边缘.

1.2 本文使用的算子

在本文中，取m=1/16，n=3/8来构造算子，这样就可以得到一组新的水平和垂直算子，分别为：

(8)

用这两个新的模板分别与原始图像作卷积运算，即可分别得出横向及纵向的梯度近似值.假设I为原图像，gx与gy分别为对图像水平方向和垂直方向进行卷积运算后所得的响应，则有如下公式：

(9)

由gx和gy可以计算出图像每个像素的梯度大小及方向:

(10)

将计算得到的梯度值g作为图像在该像素新的灰度值，这样就可以得到一副体现边缘幅度的图像.由于图像在边缘附近的亮度变化比较大，可以通过设定阈值使图像二值化，灰度值大于阈值的点认为是边缘点，反之则不是边缘点，从而实现边缘检测.

2 空间矩亚像素边缘提取

空间矩边缘检测法是Lyvers等提出的一种利用边缘灰度空间矩来检测直线边缘亚像素位置的方法，采用在单位圆建立理想的二维阶跃边缘的模型，如图1所示.图中h是单位圆内的背景灰度，k是阶跃高度，l是圆盘中心到直线边缘的垂直距离，l∈[-1,1]；φ是边缘与y轴的夹角，φ∈(-π/2,π/2).

图1 理想二维阶跃边缘模型

连续函数f(x,y)的(p+q)阶空间距定义为

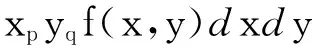
(11)

为了降低问题的维数，可以将窗口旋转φ角，使边缘与x轴垂直，旋转后的空间矩为

(12)

由式(12)可知:

(13)

(14)

(15)

(16)

(17)

旋转后的各阶矩与边缘参数的关系为：

(18)

(19)

(20)

(21)

假设(x,y)为像素点的图像坐标，(x′,y′)为亚像素边缘检测结果，单位圆所包含区域为N×N邻域，则可以得到像素点的亚像素边缘位置：

(22)

对每一个边缘像素点重复上述步骤,可以获得每一个像素点的边缘参数，就可以得到图像的边缘以及相应的亚像素位置.

3 实验及分析

实验使用lena灰度图像进行边缘检测，首先使用新构造的算子对图像进行边缘检测，确定和保存图像边缘的位置信息，在对这些边缘位置结合空间矩进行进一步的检测，原图像及结果如图2～图7所示.

图2 lena灰度图 图3 空间矩算法

图4 Sobel算子图5 新改进算子

图6 Sobel+空间矩 图7 新改进算子+空间矩

3.1 仿真结果分析

通过图2～图7可以看出，对图像直接使用空间矩的方法检测出的边缘较宽，但细节比较全面；而使用Sobel算子检测出的边缘较细，但也丢失了部分边缘信息，而使用新算子检测出的边缘在一些细节上比Sobel检测结果宽，但补全了更多的细节；由于本文所使用的检测方法是首先检测出图像的像素级边缘位置，在根据检测出的边缘信息对原图像进行亚像素级检测，这就导致了检测出的像素级边缘位置信息会对最终的检测结果有很大的影响，如Sobel算子与空间矩相结合的方法由于使用Sobel算子对边缘进行初步检测所得出的边缘信息有所丢失，导致之后使用空间矩检测时也丢失了部分边缘；而在同等检测条件下，使用新算子比Sobel算子检测出的边缘有更多细节，这使得在之后利用空间矩进行亚像素检测时，本文使用的方法所检测出的边缘细节更丰富.

3.2 边缘坐标检测结果

在lena图像中随机抽取四组边缘点检测其坐标位置，如表1所示：

表1 边缘点坐标及测出的亚像素坐标

表中，(x,y)表示检测出的像素级坐标位置，(X,Y)表示相应边缘点的亚像素坐标位置.不论是使用Sobel算子检测初始边缘，还是使用改进算子检测，由于都会用到空间矩来确定亚像素位置，因此，两种方法测出的位置坐标相同，然而由于利用改进算子测出的边缘更丰富，因此，本文算法能够检测出更多边缘的具体位置.

3.3 仿真时间分析

对图像边缘检测时间进行记录可知，使用空间矩方法需要时间6.296 s，而使用Sobel算子与空间矩相结合的方法检测只需要0.689 s，本文所使用方法用时1.568 s，通过比较可知在检测出边缘像素位置后再进行亚像素位置的检测耗时较短，本文所使用方法用时比Sobel算子结合空间矩方法耗时长的主要原因是本文使用新算子检测出的边缘信息较多，导致使用空间矩进行检测时增加了运算量.由此可知，随着图像边缘复杂程度的增加，检测边缘用时也会大大增加.

4 结论

本文根据梯度算子的推导方法提出了一种改进的新梯度算子，用以检测图像的像素级边缘，同时结合5×5空间矩方法对图像进行亚像素边缘检测，该方法首先使用改进算子对图像进行边缘检测，确定边缘位置后，对边缘位置信息进行记录，然后根据记录下来的边缘点坐标对原灰度图使用5×5空间矩算子进一步的检测，确定边缘的亚像素位置.根据实验结果，在同样的边缘检测条件下，本文所使用的改进后的算子检测出的边缘更加全面，但是由于利用空间矩方法需要对每个像素都进行模板操作，且使用新算子检测出更多的边缘细节信息，因此处理边缘复杂的图像耗时较长，实时性不理想，需要作进一步改进.

[1]刘涵,郭勇,郑岗,等.基于最小二乘支持向量机的图像边缘检测研究[J].电子学报,2006,7(7):1275- 1279.

[2]丁兴号,邓善熙.基于小波变换的屋脊边缘亚像素检测[J].哈尔滨工业大学学报,2004,11(36):1480- 1482,1530.

[3]王青竹,王珂,袁国良,等.多层次自适应空间系数高斯小波图像边缘检测[J].中国图像图形学报,2009,14(7):1347- 1351.

[4]LEE J,HARALICK R M,SHAPIRO L G.Morphological Edge Detector[J].IEEE Trans.Robotics and Auto-mation,1987,3(2):142- 153.

[5]QU G Y,WOOD S L.Edge Detection Using Im-proved Morphological Gradient[J].In:Proc.of IEEE Conf.Signals,Systems and Computers,1998,2(1):954- 958.

[6]PAL S K,KING R A.Image enhancement using fuzzy sets [J].Electronics Letters,1980,16(10):376- 378.

[7]LEILA FALLAH ARAGHI,MOHAMAD REZA ARVAN.An Implementation Image Edge and Feature Detect-ion Using Neural Network[J].Proceedings of the International Multi-Conference of Engineers and Computer Scientists,2009,1(3):18- 20.

[8]KRIS JENSEN,DIMITRIS ANASTASSIOU.Sub-pixel edge localization and the interpolation of still im-ages[C].IEEE Transactions on Image,1995,17(6):629- 634.

[9]LI X,ORCHARD M T.New edge directed inter-polation[J].IEEE Transactions on Image Process-ing,2001,10(10):1521- 1527.

[10]EDWARD P LYVERS,OWENROBERT MITCHELL,MARK L AKEY,et al.Sub-pixel measurements using a moment-based edge operator[C]. IEEE Transac- tions on Pattern Analysis and Machine intelligence,1989,11(12):1293- 1309.

[11]TABATABAI A,MITCHELL O R.Edge location to subpixel values in digital imagery[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1984,6:188- 201.

[12]赵爱明.基于二次曲线拟合的图像亚像素边缘定位算法[J].哈尔滨理工大学学报,2006,11(3):68- 70.

[13]贺忠海,王宝光.利用曲线拟合方法的亚像素提取算法[J].仪器仪表学报,2003,24(2):195- 197.

[14]马晓路,刘倩,胡开云.MATLAB图像处理从入门到精通[M].北京:中国铁道出版社,2013.

A Sub-Pixel Edge Detection Method based on Improved Operator and Spatial Moment

WEI Xiyang,ZHANG Xuxiu

(School of Electrical and Information Engineering,Dalian Jiaotong University,Dalian 116028,China)

A new gradient operator is presented based on Sobel operator to detect the image edges,and the sub-pixel edge position can be located by using spatial moment to detect original image. At the same time,the detection results are compared by using the Sobel operator and new gradient operator.The result shows that more edges are found by the new operator under the same edge-udging conditions.

sobel operator;spatial moment;sub-pixel;edge detection

1673- 9590(2016)03- 0117- 04

2015- 09- 11

国家自然科学基金资助项目(61471080/F010408)；国家科技支撑计划资助项目(2015BAF20B02)

魏希扬(1990-)，男，硕士研究生；张旭秀(1968-)，女，教授，博士，主要从事控制理论、智能控制、信号处理的研究E-mail: zhangxuxiu@163.com.

A