浅谈乐学单中探究活动的设计
王晓娇
【中图分类号】G623.5 【文献标识码】A 【文章编号】2095-3089(2016)23-0240-01
随着基础教育改革不断向纵深发展,课堂教学逐渐回归理性,从课改之初的沸沸扬扬追求表面热闹的形式主义,到如今渐渐做到踏实、扎实、务实,新理念的提出、新方法的应用,都越来越使课堂教学更加高效。我校在近年来不断实践,在数学教学中尝试以“乐学单”的形式加强师生互动,打造高效课堂,取得了较好的教学效果。下面就 “乐学单”在活动设计方面,谈谈几点看法。
“乐学单”是课堂上发放给学生的引导性学习材料,我们将一份“乐学单”的设计分为四个部分:学习目标、准备活动、探究活动及练习活动。这里主要谈一谈探索活动。
新课标指出:教师要让学生在有效的数学活动中理解和掌握基本的数学知识与技能、思想与方法。因此,我们十分重视乐学单的活动环节的设计。通过探索方法、尝试应用,取得了较好的教学效果。在活动设计上,做到了以下几个方面:
一、问题精炼,启迪思维
乐学单的探索活动是针对本课的教学重点及难点进行设计的,通过有效的学习活动,使学生经历知识的探究过程,建立数学模型,达到对新知的深入理解,实现对知识的内化。因而,每课的探究活动,应紧紧围绕知识重点,指向明确,少而精准,通过一两个活动,实现学生对知识的掌握。
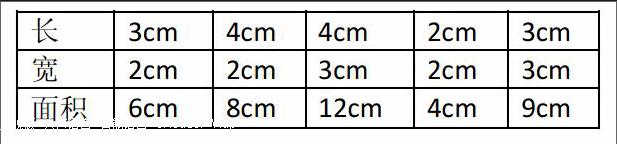
例如:长方形和正方形的表面积一课的乐学单,设计了两个探索活动。1.用面积为1平方厘米的小正方形拼出长方形或正方形,看看拼出的图形的面积与长、宽及边有什么关系; 2.测量乐学单上的长方形和正方形的边的长度,计算出它们的面积。本课就围绕这两个活动展开,通过第一个开放性的操作活动,学生填写了以下表格:
通过对表中数据的分析,讨论得出长方形和正方形的面积的计算公式。
接下来,通过第二个实践活动,学会计算给定的图形的面积,运用所学知识及时尝试解决问题。
本课,学生根据乐学单的提示,带着明确的学习目的开展探究活动,一边做,一边悟,每一个活动的设计都体现了知识内涵,实现了重难点突破,真正做到了有的放矢。学生在乐学单的引导下,经历了知识的形成过程,及时进行了归纳总结,成功建立了数学模型,并能运用知识解决问题,有效掌握了知识,提升了能力。
二、全体参与,互动提高
乐学单的探究活动设计,要尽可能给学生提供发展的条件,尽量使每个学生都能够动手、动脑、动口,多种感官参与到学习活动中来,使学生有更多的学习机会。虽然他们的思维水平高低不同,但人人亲历了探索知识的过程,参与了丰富、生动的思维活动,在活动中充满自信的学习,平等主动地交流,合作解决问题,主动性得到了充分发挥。
如:教学分数的意义,在第一课时学生初步了解了分数的意义,知道把一个物体看成“单位一”,平均分成若干份,表示这样一份或几份的数,叫做分数。第二课时将对分数的意义进行拓展 ,使分数表示。学生知道“单位一”不仅可以是一个物体,由若干个物体组成的整体也可以看做是“单位一”,用分数表示。针对这一目标,我将乐学单的探究活动设计为:1.讲方格纸(九宫格)涂上红黄蓝三种不同的颜色,说一说得到的分数表示的意义;再剪开,说分数的意义。2.把6个圆片平均分,看看可以得到哪些分数。
在这里,教师给每个学生提供了学习的素材,让学生通过在大正方形中涂色,说分数的意义,激活已有知识,在此基础上,学生通过“剪”与“摆”,认识到“整体”所发生的变化。通过分圆片,体会到将整体平均分的过程,认识到分的份数不同,得到的分数也不同。在这个过程中,全体学生都投入了探究过程,每个学生多种感官参与学习,丰富了学习体验,深化了感性认识。学生在剪正方形之前,思维停留在原有的认知水平上,而一“剪”就剪出了一个新的问题:分数的意义发生了变化。是什么引起了这一变化?学生的思维发生了碰撞。这时,适时的师生互动和生生互动,使学生在操作中交流,在交流中思考,在思考中领悟,使知识进一步得到了内化。
三、层次清晰,梯度深入
乐学单的探究活动设计要讲究一个层次性。要由易到难,由具体到抽象,做到环环紧扣,后一个层次应在前一个层次上延伸发展。层次要清、要到位,层与层之间是递进关系,层次与层次之间要有衔接,过渡要自然,一个层次结束之后要有个小结,再过渡到下一层次。要做到精讲多练、环环相扣、逐步渗透、逐层深化,这样一节数学课的知识呈现和能力培养就比较分明了。
如,我在一年级的《找规律》的探究活动设计中,先由学生从喜闻乐见的情境中,发现实物排列的规律;再由实物规律中抽象出其中蕴含的数字规律,当学生理解数的排列规律后,再安排较复杂的数的规律,在一系列的探究活动中,学生不断有新发现,不断有惊喜,课堂由此而变的妙趣横生,引人入胜。学生在乐学单的引导下,移步换景,思维不断向纵深发展,取得了较大的学习收获。
同时,乐学单的层次性不仅体现在知识梯度上,更重要的是面向全体孩子,让不同层次思维水平的学生都能有不同的收获。因此,探究活动在“度”的把握上尤为重要,在设计问题时要难易适中,不仅要考虑提什么样的问题,还要考虑为什么提这样的问题,使每一个问题既为活跃学生的思维服务,又能够成为完成本堂课教学任务的一个有机组成部分。问题的设计要针对学生的实际认知水平和思维能力,找到问题的切入口。心理学认为,人的知识水平就是在“已知区”“最近发展区”“未知区”三个层次之间螺旋上升,课堂提问不宜停留在“已知区”与“未知区”,即不能太易或太难。教师要努力探索如何抓住学生“已知区”与“最近发展区”的结合点,让每一个学生积极开展思维活动,杜绝优生活跃、差生兴趣不高的课堂缺陷,使各层次、各类型的学生在课堂上都有自己的位置,各尽所能,各有所得。
例如,教学《认识人民币》一课,乐学单设计了如下问题: 1.观察各种面值的人民币,给这些人民币分分类,有几种分法? 分类时遇到了什么问题?2.新版人民币与旧版有什么不同?哪些内容是不变的?问题设计由具体到抽象,一环紧扣一环,层层递进,不同发展水平的学生都有话可说。随着对问题讨论的深入,学生的思维也沿着一定的坡度发展提高。由此可见,乐学单在设计问题时,也应该尽可能多角度地提问,由易到难,由表及里,以便拓宽学生思维的广度和深度,满足不同层次学生的需要,提高学生的思维能力。
以上,是我在乐学单使用过程中的一些体会,通过不断尝试,不断反思,不断提炼,不断修正,乐学单已经在我们的课堂教学中发挥出越来越好的效果,学生的学习积极性更高了,课堂愈发焕发出生机与活力。今后,我们将继续探索,不断完善,使每个孩子都更加乐学,好学!

