初中生数学实验观的现状分析与教学建议

孙朝仁

摘要：现代数学观的发展，已由静态的绝对主义的数学观向动态的拟经验主义的数学观转化，数学实验观则属于动态的数学观范畴。基于对417名初中生的问卷调查和访谈，结合课堂观察，了解数学实验观的5个梯级现状水平，发现初中生数学实验观念系统尚未真正形成。建议采取注重问题设计方案的实验性、重视教材中实验素材的使用性、强化问题解决实验的价值性等实践性举措，以促进初中生数学实验观的形成。

关键词：数学实验观；调查；教学建议

中图分类号：G633.6 文献标志码：A 文章编号：1673-9094（2016）10A-0048-05

数学观的现代发展，已由静态的绝对主义的数学观向动态的拟经验主义的数学观转化。[1]前者认为数学是数学知识的简单汇聚，后者则认为数学是人类的一种创造性活动，它是一个由数学理论、数学方法、数学问题和数学特有的符号语言等多种成分所组成的复合体。这种复合体是人类创造性活动的产物。著名的哲学家Lakatos认为，数学是既含有经验成分又含有理性成分的一种非封闭的演绎系统即拟经验的体系。就数学的研究过程、数学与其他科学的关系层面而言，数学具有形象性、似真性、拟经验性、可证伪性的特点，对这些特点的强调就是为突出观察、实验、分析、比较、归纳、联想、想象等思维过程的重要性。而数学实验恰好是反映这些具有创造性思维成分的重要载体，符合初中生知觉思维水平、抽象思维尚待完善的特点，因此探讨初中生数学实验观对初中数学教育意义重大。

同时，皮亚杰的认知发展理论与建构主义思想、弗赖登塔尔的“再创造”理论、迪恩思的四个学习原则（活动原则、结构原则、数学化原则、知觉变化原则）和学习过程的六个阶段理论、比格斯的“实验室法”、施瓦布“探究性学习法”、杜威的“做中学”理论等为“数学实验观”的形成提供了丰富的理论依据，因此研究以“做”为表征的初中生数学实验观，其价值毋庸置疑。

一、数学实验观的认识

“数学实验观”属于动态的数学观，是指学生在学习过程中建立起来的自觉“做”数学的习惯化意识水平，是关于数学实验内涵、思想方法及其应用价值的综合性认识。荷兰范希尔（VanHiele）夫妇把几何思维划分为5个水平；水平1：直观（visuality）；水平2：分析（analysis）；水平3：非形式化的演绎（informaldeduction）；水平4：形式的演绎（formaldeduction）；水平5：严密性（rigior）。把这“5维划分法”借用到数学实验认识论领域，则反映数学实验观水平的5个梯级层次。水平1：面对实验素材有“做”实验念头，但没有意识到数学实验的直观作用；水平2：意识到数学实验的直观作用，但仍流于任务性分析水平；水平3：习惯于单一实验方法并进行非形式化拓展，但没有意识到同一模型可以有多种实验方法；水平4：面对棘手问题，有借助实验发现问题解决突破口的意识，在直观发现的基础上进行多种形式化运演；水平5：面对困难问题组，有借助实验直觉性发现问题解决的思维惯习，自觉优化解题方案和隐性变式。

二、现状调查与分析

为把握学生数学实验观念水平，促进基本活动经验积累的指向性教学水平，针对初中学生数学实验观的现状，采用问卷、课堂观察和结构性访谈相结合的方式进行调查分析。基于以上5层次水平划分法分析，在查阅文献的基础上编制初始问卷，经历试测并修改完善，研制出“初中学生数学实验实验观的调查问卷”。以某市部分初中学校共426名学生作为研究对象（电脑随机确认），于2015年1月，在不同层次4所中学进行问卷调查，共发放问卷426份，收回有效卷417份，有效回收率98%。问卷回收后，采用SPSS Statistics13.0软件进行统计分析。

（一）初中阶段学生数学实验观的基本概况

初中阶段学生的数学实验观的现状调查与分析（如表1）。

从表1可以看出，学生对数学实验帮助学习的看法中，认为“帮助很大”的占33.8%，“有些帮助”的占51.1%。因此，可以确认初中学生基本认同数学实验对数学学习的帮助。换句话说，数学实验是初中学生数学学习不可或缺的一种方式，对数学思维发展起一种直观的补助作用。对于“是否愿意用数学实验方式进行学习”的问题，选择“不太愿意”和“不愿意”的共占5.2%，这就从反面说明绝大多数初中学生喜欢用数学实验的这种蕴含天性的学习方式进行数学学习，这与数学实验先期调查数据有明显的差异：先期调查数据显示“愿意”以上的学生占89%，而本次调查高达94.8%，这说明数学实验观念渐次深入人心。对于“用数学实验解决问题的实践”这一问题，选择“经常”的只有9.6%，选择“偶尔遇过”的学生占61.1%。这表明仅有不到1成的学生经常借助数学实验解决问题，9成以上的学生数学实验的观念不强，数据的背后反映了数学实验观念系统尚未真正形成，由“愿望”到“行动”还有很长的距离；另一个侧面说明，传统的标准化学习方式依然根深蒂固。在访谈中也了解到学生（尤其是学优生）认为数学实验的“过程性”，会耽误好多时间，尽管“经历”能变迁为“客观经验”，在“作业”压倒一切的学习时代，数学实验观念具有政策和教育指向的局限性。

（二）初中阶段学生对不同“知识类型”实验的看法

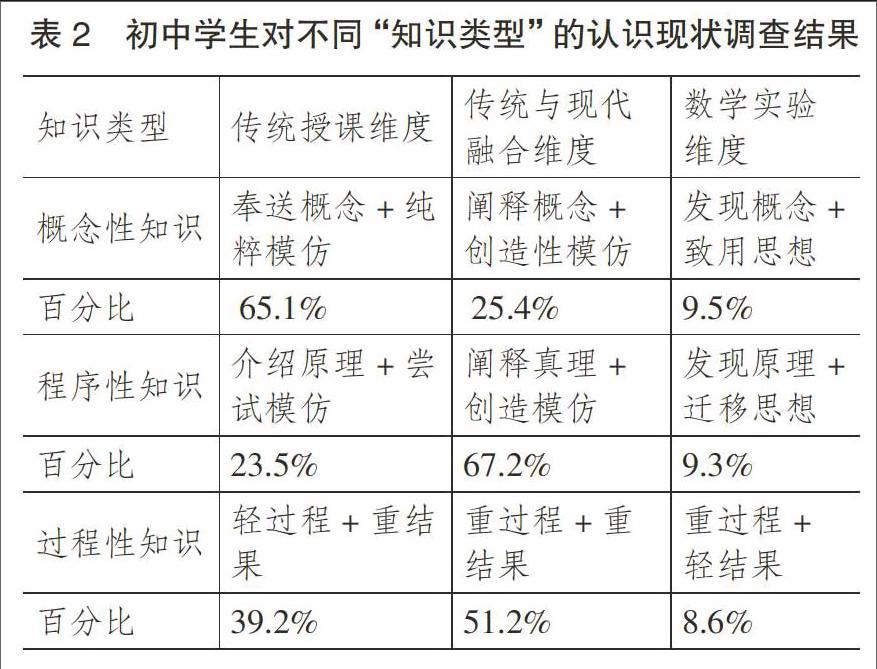
初中阶段学生对不同“知识类型”的认识调查与分析（如表2）。

从表2可以看出，对于“概念性知识”用数学实验方式处理的仅占9.5%，说明不到1成的学生意识到概念发生、发展和形成过程的重要性。这在很大层面上源于概念的“规定性”认识观念根深蒂固，这与裴光亚先生所说的数学不允许有“前概念”是一脉相承的，忽略了数学教育是可以有“前概念”的说法。这有悖于裴光亚先生的“最好的老师是发现真理，最差的老师奉送真理，介于两者之间的是阐释真理”的现代数学教育观的主张。对于“程序性知识”用数学实验方式处理的只占9.3%，说明也只有不到1成的学生意识到原理（公式、法则）发现的重要性，也与传统的“记忆+模仿”的原理课惯习分不开的。而“阐释真理+创造模仿”具有数学实验的倾向性占67.2%，说明数学实验观形成形态良好，而“创造模仿”意味着变式化倾向明显，这就从另一个层面说明，中国传统变式教育的优良传统对中国数学教育的巨大贡献。对“过程性知识”用数学实验处理的方式即重视过程性占47.8%，这表明重视知识产生过程的比例呈上升趋势，改变了传统的“唯结果”的教育观，这与“课标”倡导“课程内容组织要重视过程，处理好过程与结果的关系”的精神是一致的。“过程大于结果”“过程与结果并重”是数学实验教学的终极目标，实验更重视过程，唯有直观的过程方能产生突如其来直觉的创造性，因此过程性知识需要过程成就，要重视过程意义丰富的数学实验观培养。endprint

（三）初中阶段学生对不同“课型”数学实验方法的看法

初中阶段学生对不同“课型”的实验方法的看法调查与分析（如表3）。

数学课堂通常分为若干模块，其中概念课、原理课（也叫规则课）、习题课是教学的主体。从表3可以看出，对于“概念课”，采用“再发现过程法”即实验法的高达78.1%，即有近8成的学生能自觉借助数学实验理解概念，这说明数学实验在概念的形成和理解层面为学生提供了很大的帮助。就概念形成的心理过程而言，抽象和概括是掌握概念的前提和基础，而数学实验为抽象、概括提供了直观可行的抓手，因此数学实验是学生理解概念的有效工具。对“原理课”，采用几何背景意义法即学生借助实验活动法来理解规则的比例高达67.9%，也就是说有近7成的学生能主动借助实验的直观性理解抽象的数学原理，这说明数学实验能为抽象原理的认知理解提供几何直观。比如“因式分解”的抽象性，借助符合条件的长方形面积与边长的关系就能直白的显化，化隐为明、化抽象为具体，体现了数学实验观确立的本质初衷。对于“习题课”，采用内源变式思维法的学生有79.1%，多维建模法的有20.9%，也就是说有8成学生习惯变式思维，这和“智慧技能学习的唯一有效方法就是建立在理解基础上的变式练习”的学习传统是分不开的。先期数学实验“揭示三角形内角和定理本质”的调查数据显示：有52.1%的同学能用变式实验法把握原理内涵。这些变式思想和高级意识都是学生的创造潜能得以发展的地气，因此培养“课型”实验观至关重要。

（四）初中阶段学生对数学实验内源作用的看法

初中阶段学生对数学实验内源作用的看法访谈分析（如表4）。

S.Pirie和T.Kieren的超回归数学理解模型。[2]超回归数学理解模型由8个不同理解水平组成，即：原始认识、产生表象、形成表象、性质认知、形式化、观察评述、构造化、发明创造。这8个理解水平包括了人们理解某一数学知识（概念、公式、原理等）所经历的全过程。从表4可以看出，“原始认识”水平占98.3%，说明数学实验几乎能唤醒每一位同学已有认知经验；迁移水平占9.3%，说明数学实验作用倾向于高级思维认识，本源性迁移作用不明显，要强化学生的“后台经验”图式，使其转化为“缓存经验”，便于支取，方能提升由“知”到“识”能力迁移的水平，“打通”问题的突破口。“形成表象”水平占74.5%，表象是人脑对客观事物的印象，这说明在数学实验的帮助下大多数学生的思维水平都能达到现有知觉水平，而迁移赋值仅为27.9%，说明表象对内源思维建构的迁移作用不明显，数学实验在这一思维层面应该渗透功能性培育意识。“形式化”水平占40.1%，也就是说数学实验帮助学生形成“一般化”产生式系统的能力比较强；迁移水平占47.5%，说明有近一半学生的思维图式经验的跃迁来自于数学实验内源建构思维的作用。从数学教育视角证明，学生运用数学知识解决实际问题能力和创造力并不呈正态分布。“创造发明”水平占比例是7.8%，这说明不到十分之一的学生在数学实验的帮助下能产生创造的直觉思维；迁移水平却高达84.8%，说明数学实验对学生经验迁移能力作用显著，这与“每个学生都拥有运用数学知识解决实际问题和创造力的潜能”研究结论是一致的。[3]

从访谈显示的数据来看，数学实验“5层级水平观”建立意义重大，无论是创造潜能还是简单化思想都是“上位”的行事观，直接影响人生能力和生命质量。

三、教学建议

积累活动经验是提高学生数学素养的“关键性标志”，是数学课堂教学的重要目标。数学实验作为理解数学的特殊工具，本身带有积累活动经验的个性特征，因此，让学生形成自动化实验观念意义重大。而实验观念产生、形成、发展需要教师的实践性引领，方能让行动成就观念，让观念反哺行动，进而落实课程教育素养性目标。

（一）注重问题设计方案的实验性

调查数据表明，对于“用数学实验解决问题的实践”这一问题，选择“经常”的只有9.6%。这说明大部分学生的数学实验观念系统尚未形成，这就要求教师要加强教学引领，关注问题设计实验倾向的研究和示范，凸显实验性，方能在实验意识的渗透中形成稳定的实验心理特征，进而初步形成实验观念。比如，苏科版七年级上册《丰富的图形世界》教学，可以通过制作几何体、认识几何体（摸几何体和说几何体面、棱、顶点的特征）、设计几何体方案三模块学习。让学生通过动手操作，理解从平面到空间的转换过程，认识简单几何体的基本特征。设计这种实验倾向的问题串意义不止于理解知识，更在于形而上素养积累，落实课程生命观。

（二）重视教材中实验素材的使用性

用数学实验方式理解“过程性知识”的学生占47.8%，这说明有近一半的学生意识到，数学实验对过程性知识理解起着不可替代的作用。为引领更多学生参与实验理解“过程性”“程序性”知识，建议重视实验素材的可使用性。换句话说，就是对课本呈现的实验素材进行全角发掘其实验功能，让学生在实验组织系统样板实践中，不自觉形成实验的依赖性，进而养成“每一个学生”的实验观。比如，苏科版七年级第105页数学实验室《月历游戏》可全角拓展设计流程：猜数游戏、算数游戏、设计游戏、拓展游戏，以月历为工具，通过游戏的形式展开实验过程，在游戏中揭示月历的排列规律，进而形成用列一元一次方程来解决问题的意识。这种由“猜想”到“实践”到“创编”的命题实验意识，使得学生形成模块性实验系统，有利于实验观的定性养成，提升实验的知觉水平，落实课程教育发展观。

（三）强化问题解决实验的价值性

对于“概念课”，采用实验发现法的学生占78.1%，说明学生的数学实验观念在概念理解领域初步形成；学生实验超模型的“形式化”思维水平占40.1%，说明一部分学生意识到借助实验有利于“一般化”图式产生，而“形式化思维”标准下的学生的迁移水平占47.5%，说明数学实验内源建构思维的作用比较显著。为拓展学生现有实验观念意识区，建议强化提升问题解决实验倾向的水平，体现实验的价值性，让学生在初级实验观念的指导下，由原初实验观上升为结构实验观，进而形成带有鲜明个性的数学实验惯习。比如，无理数概念的建立，可以通过两组实验来深化认识。实验1：在数轴上表示面积为2的正方形的边长 所对应的点（实物操作、计算机模拟）；实验2：在数轴上表示圆周率 所对应的点（实物操作、计算机模拟）。这样设计问题倾向有利于学生直观理解“无理数也可以用数轴上的点表示”。这种在变异理论指导下的实验倾向，有利于把握概念的本体价值，使得抽象因具体而抽象，具体因抽象而具体，反映数学实验的本源价值，落实人文素养课程观。

“问题设计方案的实验性”侧重于“做”实验的念头和实验“直观”性认识水平；“实验素材的使用性”意味着多维度地解释同一模型；而“问题解决实验的价值性”则反映实验“突破”意识和直觉的“从天而降”的创造价值，这些基于“理解数学”的实验意识观与数学认知过程包括感知觉、注意、表象、记忆、数学语言、数学思维与意识等过程性形态意识是一脉相通的，强调了数学实验观建立的发展性意义。

参考文献：

[1]喻平，董林伟，魏玉华.数学实验教学：静态数学观与动态数学观的融通[J].数学教育学报，2015（2）：26-28.

[2]李淑文，张同君.“超回归”数学理解模型[J].数学教育学报，2002（2）：21-23.

[3]王延文，王光明.数学能力研究导论[M].天津：天津教育出版社，1999.

责任编辑：徐瑞泰endprint