基于U模型的混沌系统Super-Twisting同步控制研究

张建华，李 杨，吴学礼，赵 民，庄沈阳

(1.河北科技大学电气工程学院，河北石家庄 050018；2.河北省生产过程自动化工程技术研究中心，河北石家庄 050018；3.河北科技大学信息科学与工程学院，河北石家庄 050018；4.齐齐哈尔大学计算机与控制工程学院，黑龙江齐齐哈尔 161006)



基于U模型的混沌系统Super-Twisting同步控制研究

张建华1,2，李 杨2,3，吴学礼1,2，赵 民1，庄沈阳4

(1.河北科技大学电气工程学院，河北石家庄 050018；2.河北省生产过程自动化工程技术研究中心，河北石家庄 050018；3.河北科技大学信息科学与工程学院，河北石家庄 050018；4.齐齐哈尔大学计算机与控制工程学院，黑龙江齐齐哈尔 161006)

提出了一种基于U模型的混沌系统Super-Twisting同步控制方法，对混沌系统的混沌控制进行了描述，结合混沌系统的研究现状和非线性系统设计中的一些成果，提出了混沌控制与同步的一些新方法，设计出相应的控制器实现有限时间混沌同步控制。针对Lorenz 系统和Chen系统进行了数值仿真，仿真结果证明了所给方法的有效性。

稳定性理论；混沌系统；同步；U模型；Super-Twisting算法；有限时间

混沌现象广泛地存在于自然界，它是非线性系统所包含的一种比较特殊的复杂运动。混沌是一种非线性系统的动态形式，其明显特点是对噪声和初始值的敏感性。类似随机现象是混沌现象在确定性系统中本身固有的一种特性。混沌现象揭示了自然界及人类社会中普遍存在的统一性问题，即复杂性与有序和无序、确定性和随机性彼此间的统一，加深了人们对客观世界的认识。“混沌”是近代非常引人注目的热点研究问题，它掀起了继相对论和量子力学以来基础科学的第三次革命。在现实生活和实际工程技术问题中，混沌无处不在，揭示了随机现象背后可能隐藏的简单规律[1-2]。

混沌同步原理是PECORA和CARROLL在1990年提出的，在非线性系统研究中，混沌系统同步控制已成为学者们研究的热门领域[3]。混沌同步的研究受到了包括通讯、信息科学、医学、生物、工程等领域中大量研究人员的关注[4-6]，包括线性反馈[3]和自适应[4]等方法实现同步[5]和反同步[6]等控制，具有很大的应用潜力和发展前景[7-9]。所谓混沌系统同步控制，是指一个混沌动力学轨道收敛于另一个混沌动力学轨道，以致两个系统始终保持步调的一致[10-11]。近年来，学者们提出了很多有关混沌同步的方法[12-13]应用到同步控制的设计过程中，如反推控制、延时反馈控制、基于观测器控制和滑模控制等。

滑模控制能够克服系统的不确定性，对干扰和未建模动态具有很强的鲁棒性，尤其是对非线性系统的控制具有良好的控制效果[14-16]。U模型为传统的非线性系统构造了一个通用的模型结构，相对于其他方法的优点:U模型可以采用时变参数多项式的方式表示一大类平滑非线性系统，而且U模型的形式不会使对象的非线性特性有任何损失，可以优化非线性系统的控制器部分的设计；U模型可以将非线性动态模型转换为一类仅有伪输入的参数时变非线性多项式模型，它的提出将为非线性对象控制系统设计提供一个良好的发展方向；U模型可以把繁琐的模型转换到一种简洁的结构模型[17-18]。

Super-Twisting算法[19-20]是一种高阶滑模控制方法，可以解决有限时间的同步控制问题，特别是通过设计严格的Lyapunov泛函[21]给出有限时间收敛性。这里借助U模型控制方法，将系统的控制输出设计为虚拟控制的控制输入，解决非线性系统的控制问题，通过Super-Twisting滑模控制的有限时间收敛特性，设计有限时间滑模同步控制器。

1 基础知识

典型的统一混沌系统，可以通过下面的系统进行描述：

(1)

式中：x1，x2和x3是混沌系统状态变量。系统参数α∈[0,1]，当0≤α<0.8时，式(1)称为Lorenz混沌系统；当α=0.8时，式(1)称为Lü混沌系统；当0.8<α≤1时，式(1)称为Chen混沌系统。

带有不确定外界扰动的混沌系统可以描述为

(2)

式中：Δ1，Δ2和Δ3是外界扰动。

用于同步的子混沌系统描述为

(3)

式中：y1,y2,y3表示子混沌系统的状态；ui指的是子系统的控制输入。

2 基于Super-Twisting算法的滑模同步控制

Super-Twisting算法[21]是一种二阶滑模控制方法，系统表示为

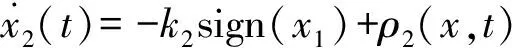
(4)

(5)

选取Lyapunov泛函为

V=ζTPζ，

(6)

于是就有

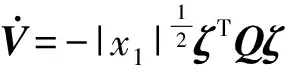
(7)

满足Lyapunov等式

ATP+PA=-Q。

(8)

考虑没有外界扰动的系统，ρ1=ρ2=0和控制增益k1,k2，于是就有如下的条件等价：

1)系统的平衡点x=0是有限时间稳定的；

2)矩阵A是Hurwitz的，也就是所有的特征值的实部都在左半平面；

3)控制增益是正数，即k1>0,k2>0；

4)对于任意正定对称的矩阵Q=QT>0，对于Lyapunov等式(8)存在正定对称解P=PT>0。对于函数V(x)，解的轨迹在t=0有x(0)=x0，会在有限时间T(x0)内达到原点，并且有如下关系成立：

关于收敛性的研究表明系统是有限时间收敛的，并且具有很好的鲁棒性。

定理1 针对主混沌系统(1)，子混沌系统(3)，对于任意的常数ki>0,li>0,i=1,2,3，设计如下的Super-Twisting滑模控制器：

(9)

其中，自适应律设计为

(10)

那么主混沌系统(1)，子混沌系统(3)可以在有限时间内达到同步。

证明 为设计控制器以实现主混沌系统和子混沌系统的同步，首先构造误差状态：

ei=yi-xi,i=1,2,3,

(11)

针对主混沌系统(1)，子混沌系统(3)可以得到：

(12)

根据U模型控制方法将控制器(9)带入可得误差系统见式(13)：

(13)

对于误差系统(13)，根据Super-Twisting滑模控制方法可以得到系统是有限时间收敛，所以主混沌系统和子混沌系统能够达到有限时间同步。

同步控制算法具有很强的鲁棒性，如果针对带有不确定外界扰动的混沌系统(2)进行同步控制，同样采用定理1中的同步控制器，误差系统表示为

(14)

3 数值仿真

为说明同步控制的性能，这里对同步控制的算法给出相应的仿真实验。

算例1 考虑如下混沌系统，主系统为

子系统为

选取定理1中设计的控制器，带入控制器之后可以得到如下结果。

通过数值仿真，选取初始条件为

(x1(0)x2(0)x3(0))T=(-5 1 5)T，

(y1(0)y2(0)y3(0))T=(0 0 0)T，

(v1(0)v2(0)v3(0))T=(1 1 1)T，

控制增益l1=1，l2=1,l3=5,

(15)

根据控制增益可以得到矩阵， 于是可以得到

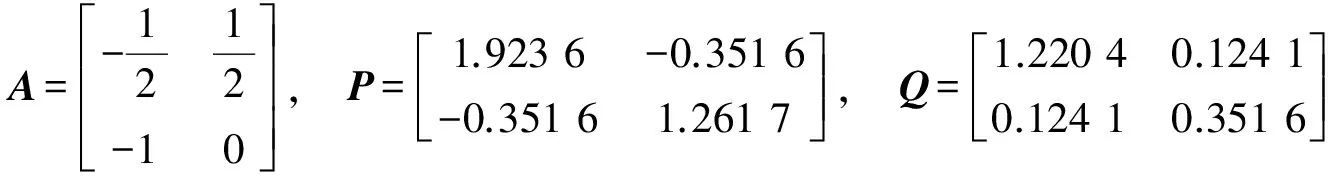
λ(P)=(1.109 8 2.075 6),λ(Q)=(0.334 3 1.237 8),

于是就有T=79.813 2，有限时间和初始条件有关，同时由于对于LMI求解过程中得到的矩阵P,Q只是满足条件的一组，所以给出的收敛时间只是说明在有限时间内收敛，很难得出系统的收敛时间。图1描述的是Lorenz混沌系统的混沌特性；图2描述的是Lorenz主混沌系统的状态x1和子混沌系统的状态y1；图3描述的是Lorenz主混沌系统的状态x2和子混沌系统的状态y2；图4描述的是Lorenz主混沌系统的状态x3和子混沌系统的状态y3；图5给出同步误差曲线。通过仿真曲线可以看出，系统中增加控制器作用之后，子混沌系统的状态是y1,y2,y3已经分别同步到主混沌系统的状态x1,x2,x3中。

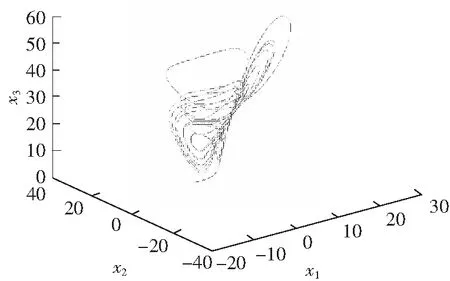
图1 Lorenz系统的混沌特性Fig.1 Chaotic attractor by Lorenz system

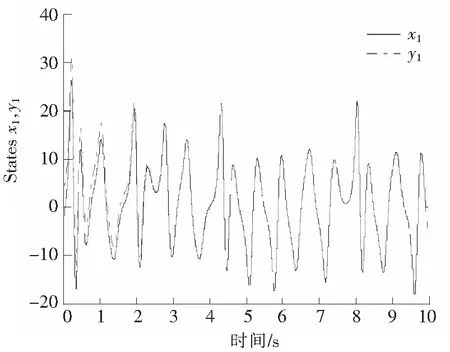
图2 Lorenz系统x1的仿真Fig.2 State trajectories of Lorenz system x1

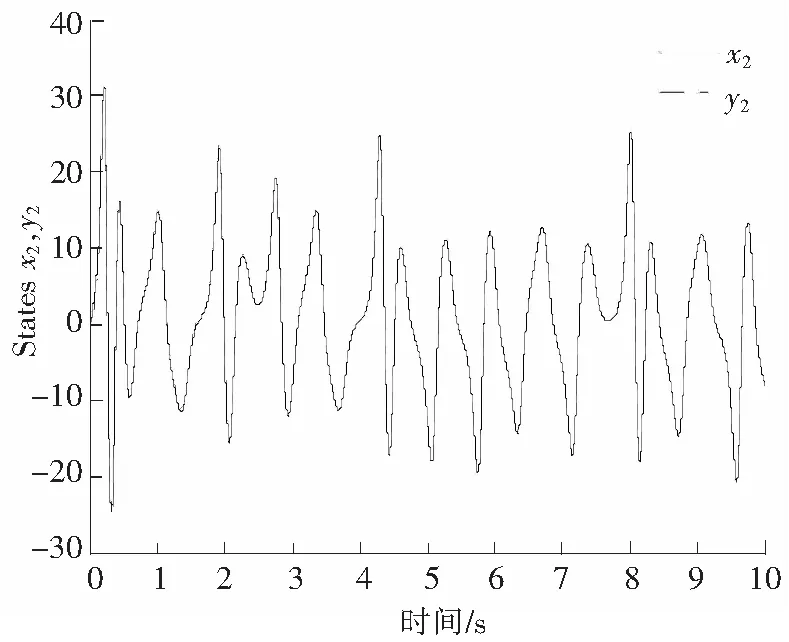
图3 Lorenz系统x2的仿真Fig.3 State trajectories of Lorenz system x2

图4 Lorenz系统x3的仿真Fig.4 State trajectories of Lorenz system x3

图5 同步误差曲线Fig.5 Error trajectories of synchronization

算例2 考虑Chen混沌系统同步控制性能，选取定理中设计的控制器，带入控制器之后可以得到。

通过数值仿真，选取初始条件为

(x1(0)x2(0)x3(0))T=(-5 1 5)T，

(y1(0)y2(0)y3(0))T=(0 0 0)T，

(v1(0)v2(0)v3(0))T=(1 1 1)T，

控制增益l1=1,l2=1,l3=5

图6描述的是Chen混沌系统的混沌特性；图7描述的是Chen主混沌系统x1的状态和子混沌系统的状态y1；图8描述的是Chen主混沌系统的状态x2和子混沌系统的状态y2；图9描述的是Chen主混沌系统的状态x3和子混沌系统的状态y3；图10给出了同步误差曲线。

图6 Chen系统的混沌特性Fig.6 Chaotic attractor by Chen system

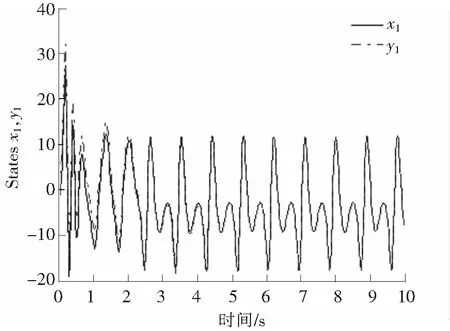
图7 Chen混沌系统x1的仿真Fig.7 State trajectories of Chen system x1

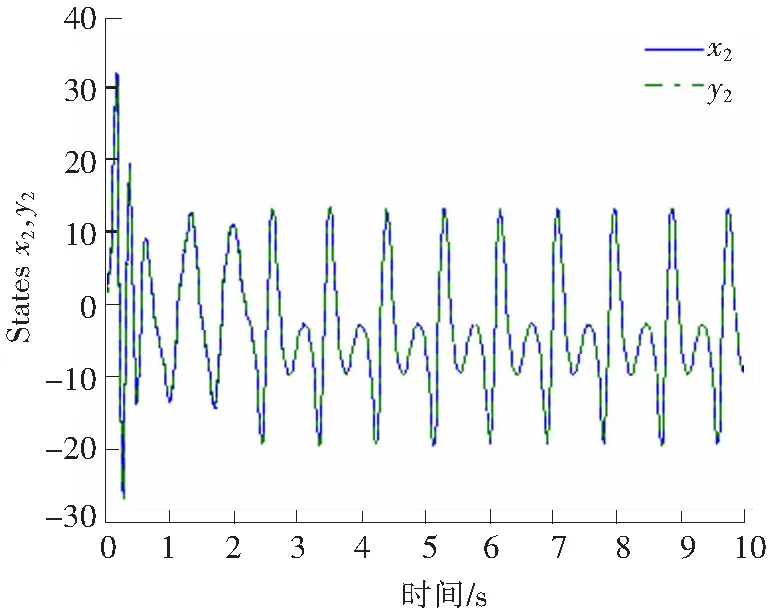
图8 Chen混沌系统x2的仿真Fig.8 State trajectories of Chen system x2

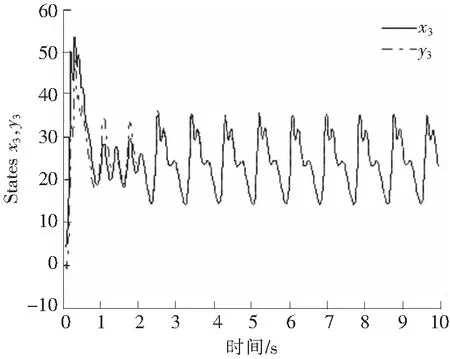
图9 Chen混沌系统x3的仿真Fig.9 State trajectories of Chen system x3

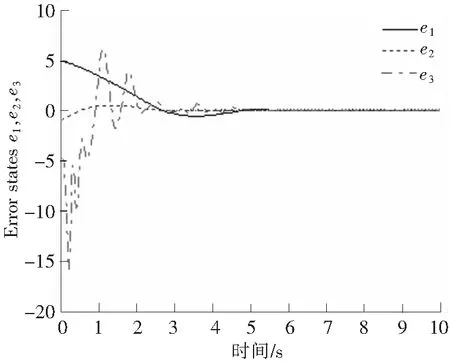
图10 同步误差曲线Fig.10 Error trajectories of synchronization

4 结 论

基于U模型的控制过程，研究混沌系统的同步控制问题，提出了一种Super Twisting混沌同步控制方法，对混沌系统进行有限时间同步控制，并计算出收敛时间。针对Lorenz 系统和Chen系统进行了数值仿真，仿真结果证明了所给方法的有效性。

[1] 于茜, 罗永健. 耦合混沌系统的自适应同步及其在保密通信中的应用[J]. 河北科技大学学报, 2011, 32(2):157-161.

YU Qian, LUO Yongjian. Adaptive synchronization of coupled system and its application to secure communication[J]. Journal of Hebei University of Science and Technology, 2011, 32(2):157-161.

[2] 邓学明. 一类非线性系统分岔混沌拓扑结构分析[J]. 河北科技大学学报, 2008, 29(3):182-193.

DENG Xueming. Analysis of bifurcation topological structure of non-linear system[J]. Journal of Hebei University of Science and Technology, 2008, 29(3):182-193.

[3] PECORA L M， CARROLL T L. Synchronization in chaotic systems[J]. Phys Rev Lett, 1990, 64: 821-824.

[4] LI Dong, ZHANG Xingpeng, HU Yuting, et al. Adaptive impulsive synchronization of fractional order chaotic system with uncertain and unknown parameters[J]. Neurocomputing, 2015, 167:165-171.

[5] GAO Xiaojing, HU Hanping. Adaptive-impulsive synchronization and parameters estimation of chaotic systems with unknown parameters by using discontinuous drive signals[J]. Applied Mathematical Modelling, 2015, 39(14):3980-3989.

[7] 吴学礼, 杨朝超, 张建华. 基于一致性理论之飞机群运动控制[J]. 河北科技大学学报,2015, 36(5):523-531.

WU Xueli, YANG Zhaochao, ZHANG Jianhua. Aircraft group control based on consensus[J]. Journal of Hebei University of Science and Technology, 2015, 36(5):523-531.

[8] 江卫华, 刘秀君, 宗慧敏. 具有共振的分数阶微分方程边值问题解的存在性[J]. 河北科技大学学报, 2014, 35(6):518-523.

JIANG Weihua, LIU Xiujun, ZONG Huimin. Existence of solutions for fractional differential equation boundary value problems at resonance[J]. Journal of Hebei University of Science and Technology, 2014, 35(6):518-523.

[9] BEHINFARAZ R, BADAMCHIZADEH M A, GHIASI A R. An approach to achieve modified projective synchronization between different types of fractional-order chaotic systems with time-varying delays[J]. Chaos, Solitons & Fractals, 2015, 78:95-106.

[10] YANG Junqi, CHEN Yantao, ZHU Fanglai. Associated observer-based synchronization for uncertain chaotic systems subject to channel noise and chaos-based secure communication[J]. Neurocomputing, 2015, 167: 587-595.

[11]YANG Lixin, JIANG Jun. Complex dynamical behavior and modified projective synchronization in fractional-order hyper-chaotic complex Lü system[J]. Chaos, Solitons & Fractals, 2015, 78: 267-276.

[12]SUN Junwei, WANG Yanfeng, YAO Lina, et al. General hybrid projective complete dislocated synchronization between a class of chaotic real nonlinear systems and a class of chaotic complex nonlinear systems[J]. Applied Mathematical Modelling, 2015, 39(20):6150-6164.

[13]GAO Like, WANG Zhihui, ZHOU Ke, et al. Modified sliding mode synchronization of typical three-dimensional fractional-order chaotic systems[J]. Neurocomputing, 2015, 166:53-58.

[14]NAGESH I, EDWARDS C. A multivariable super-twisting sliding mode approach[J]. Automatica, 2014, 50(3):984-988.

[15]BASIN M, RODRIGUEZ-RAMIREZ P, DING S, et al. A nonhomogeneous super-twisting algorithm for systems of relative degree more than one[J]. Journal of the Franklin Institute, 2015, 352(4):1364-1377.

[16]BECERRA H M, HAYET J B, SAGÜÉS C. A single visual-servo controller of mobile robots with super-twisting control[J]. Robotics and Autonomous Systems, 2014, 62(11):1623-1635.

[19]CHEN Binglong, GENG Yunhai. Super twisting controller for on-orbit servicing to non-cooperative target[J]. Chinese Journal of Aeronautics, 2015, 28(1):285-293.

[20]FEKI M. An adaptive chaos synchronization scheme applied to secure communication[J]. Chaos, Solitons & Fractals, 2003, 18(1):141-148.

[21]MORENO J A, OSORIO M. Strict Lyapunov functions for the Super-Twisting algorithm[J]. IEEE Transactions on Automatic Control, 2012, 57(4):1035-1040.

Study on Super-Twisting synchronization control of chaotic system based on U model

ZHANG Jianhua1,2, LI Yang2,3, WU Xueli1,2, ZHAO Min1, ZHUANG Shenyang4

(1.School of Electrical Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China；2.Hebei Provincial Research Center for Technologies in Process Engineering Automation, Shijiazhuang, Hebei 050018, China；3.School of Information Science and Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China；4.College of Computer and Control Engineering, Qiqihar University, Qiqihar, Heilongjiang 161006, China)

A U model based Super-Twisting synchronization control method for chaotic systems is proposed. The chaos control of chaotic systems is prescribed, then, based on the current research status of chaotic systems and some useful research results in nonlinear system design, some new methods for chaos control and synchronization are provided, and the controller is designed to achieve the finite time chaos synchronization. The numerical simulations are carried out for Lorenz system and Chen system, and the result proves the effectiveness of the method.

stability theorem; chaotic system; synchronization; U model; Super-Twisting algorithm; finite time

1008-1542(2016)03-0268-07

10.7535/hbkd.2016yx03009

2016-02-29；

2016-03-31；责任编辑：李 穆

河北省自然科学基金(F2015208128)；河北省教育厅基金(QN20140157, BJ2016020)

张建华(1980—)，男，吉林延吉人，讲师，博士，主要从事神经网络控制、滑模控制、航迹优化方面的研究。

E-mail:zhangjianhua@hebust.edu.cn

TP273

A

张建华，李 杨，吴学礼，等.基于U模型的混沌系统Super-Twisting同步控制研究[J].河北科技大学学报,2016,37(3):268-274.

ZHANG Jianhua, LI Yang, WU Xueli,et al.Study on Super-Twisting synchronization control of chaotic system based on U model[J].Journal of Hebei University of Science and Technology,2016,37(3):268-274.