基于对策论的方案选择——以制作宣传材料方案为例

◆王少青 李慧

基于对策论的方案选择
——以制作宣传材料方案为例

◆王少青 李慧

在高校的工作事务中经常面临选择一个最优方案来降低成本以保证预算的问题。以教育技术系制作宣传材料为例，根据使用原材料供应情况以及制订方案的不同，进行综合分析，从而得出最优的制作方案。

对策论；赢得矩阵；矩阵对策

AbstractIn universities questions which need us to make the best decision to reduce costs in order to keep the budget. Based on the example of making publicity materials in department of Education Technology， this article is aimed at to choose the best scheme according to the different situations which include a few programs and the using of diff erent materials.

Key words game theory； won matrix； matrix games

在高校纷杂的工作事务中，节约资源、降低预算是选择各类方案的标准。对策论是工作事物中常见的最优方案选择的有效途径。对策论通过确定局中人，建立状态集合，综合分析各个相关影响因素，获取赢得矩阵，然后通过理智行为，求解最优值，从而得出最优的行动方案，满足方案选择标准，进而指导方案的实施。

在高校纷杂的工作事务中，节约资源、降低预算是选择各类方案的标准。对策论是工作事物中常见的最优方案选择的有效途径。对策论通过确定局中人，建立状态集合，综合分析各个相关影响因素，获取赢得矩阵，然后通过理智行为，求解最优值，从而得出最优的行动方案，满足方案选择标准，进而指导方案的实施。

1 对策论简介

对策论又叫做博弈论（Game theory），是研究具有竞争或对抗性质问题的数学理论和策略［1］。其中各行动方的决策之间是相互影响的，各方在决策的时候必须将他方的决策纳入决策考虑之中，同样也需要把他方对于自己决策考虑纳入考虑之中，在如此迭代考虑情形中进行决策，最终选择最有利于自己的战略。

对策模型的构成 对策模型是指具有对策行为的模型，或者称为对策。对策模型基本要素包括局中人、策略集、赢得函数。

1）局中人。在一个对策中，有权决定自己行动方案的

对策论又叫做博弈论（参加者，称为局中人。通常用P表示局中人的集合。如果有n个局中人，则P=｛1，2，...，n｝，一般要求一个对策中至少要有两个局中人［1］。

2）策略集。在一对局策中，可供局中人选择的一个完整的切实可行的行动方案称为一个策略。其完整的行动方案是指一局对策中自始至终的全局规划，而不是其中某一步或某几步的安排。参加对策的每一局中人i，都有自己的策略集Si［1］。

3）赢得函数。在一局对策中，各局中人所选定的策略所形成的策略组称为一个局势。如果用Si表示第i个局中人所采取的一个策略，则n个局中人所形成的策略组S=（S1，S2，...，Sn）就是一个局势。当局势出现后，对策的结果也就随之确定了，即对任意一个局势S，局中人i可以得到一个赢得Hi（S）。显然，Hi（S）是局势S的函数，称之为第i个局中人的赢得函数［1］。

矩阵对策 矩阵对策又叫做两人有限零和对策，是指有两个局中人的对策，每一个局中人只有有限个策略可供选择，其中一方的赢得值即为另一方的损失值。两个局中人的赢得之和总是为零。设有两个局中人R和B，局中人R和B的策略集分别为SR=｛R1，R2，...，Ri｝和SB=｛B1，B2，...，Bj｝。当R选定策略Ri，B选定策略Bj后，形成一个局势（Ri，Bj）。对任一局势（Ri，Bj），将局中人R的赢得值记为aij，由所有aij为元素构成的矩阵称为R的赢得矩阵A：

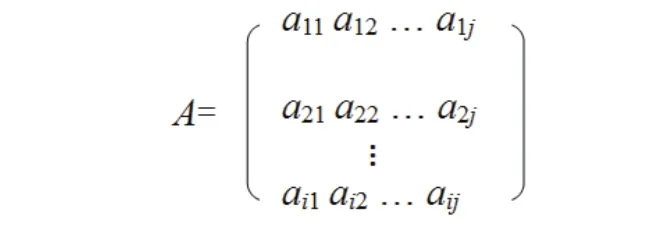
这样，矩阵对策模型记为G=｛R，B，SR，SB，A｝。

对于矩阵对策G=｛R，B，SR，SB，A｝，双方的策略集和赢得矩阵分别为SR=｛R1，R2，...，Ri｝，SB=｛B1，B2，...，Bj｝，A=｛aij｝mn。若等式（1）成立，记VG=ai*j*，则称VG为对策G的值，称使（1）式成立的局势为G在策略下的解或平衡局势，称ai*、bj*分别为局中人R、B的最优策略。在理智的情况下，局中人会采取矩阵策略中的最优策略［2］。

作者：王少青，首都师范大学教育技术系，研究方向为教育传播理论与技术；李慧，博士，首都师范大学教育技术系副教授、硕士生导师，研究方向为教育装备、教育技术学（100048）。

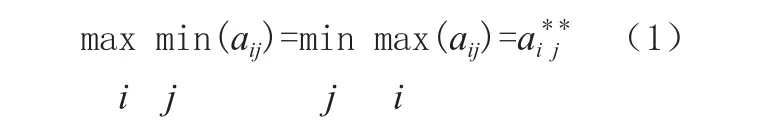
2 案例分析

某校教育技术系进行招生宣传，需要制作视频、海报、宣传册三种宣传资料。构成方案如下：

制作宣传资料共计2000套，其中视频制作预算为400元，海报制作预算为2200元，宣传册制作预算为13 000元。为了达到宣传效果，又能节约资源，同时视频宣传材料数量不能超过500张，海报不能小于300张，宣传资料要求达到2000份。

综合以上因素制订3种制作方案，如表1所示。

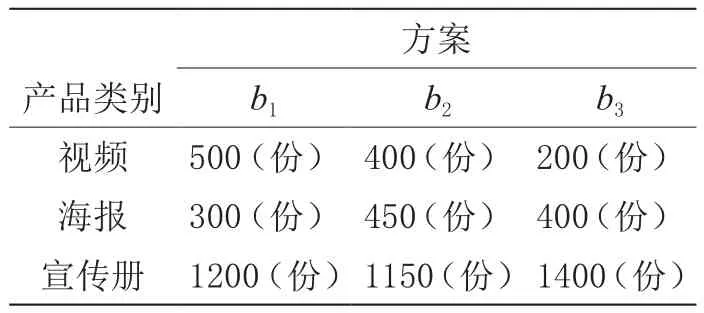
表1 制作方案

由于材料的限制因素，在材料的选择上存在以下问题。

1）①制作视频的材料全部使用CD；②由于供货迟缓，只能提供1/3的CD，其余的2/3需要DVD代替，CD与DVD的价格比为1：3。

2）①制作宣传册的资料全部使用普通喷墨打印纸；②可能由于货源不足，有1/3需要使用照片打印纸，喷墨打印纸与照片打印纸的价格比为1：1.9。

各种材料价格如表2所示。

请结合以上情况，选择出最佳构成方案，完成宣传资料的制作。

【解】根据材料供应情况，材料使用情况分为以下几种情况。

表2 材料单价

表3 材料使用方案

表4 预算和成本

1）视频材料：①全部使用CD；②2/3使用CD，1/3使用DVD。

2）宣传册材料：①全部使用喷墨打印纸；②1/3使用喷墨打印纸，2/3使用照片打印纸。

综合视频材料和宣传册材料的使用情况，会出现表3所示的4种情况。

通过题意分析可知，材料使用的4种情况属于客观情况，即形成客观条件的状态集合（共4个元素），用S1表示：

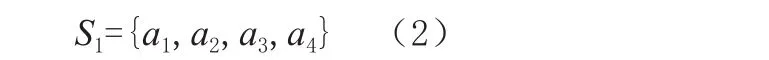
方案使用的选择属于人的选择策略，即构成人的策略集合，用S2表示人的策略集合（共3个元素）：

在此案例中，在方案、材料选择上随着材料使用情况，将问题归纳为双人对策问题，即为矩阵对策。局中人分别为人R和客观条件B，人有3种可供选择的策略，客观条件存在4种不同的状态。根据预算及成本可得出表4。

其中剩余资金公式M得：

其中，L表示每项宣传资料预算，t表示每种材料单价，Q表示各类资料数量。分别计算12种情况中的资金剩余Mij（i表示S1中材料选择的4种情况元素符号，j表示S2中3种方案元素符号）。以M11为例：

据此进行计算，得出Mij值，见表5。

由表5可得，案例中人的赢得矩阵为A：

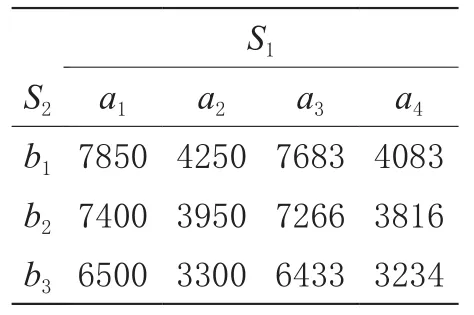
表5

从而得到矩阵对策G=｛R，B，S1，S2，A｝

在案例中材料的供应情况属于客观事件，设各种情况出现的概率相等，因此运用矩阵对策进行求解。在人的赢得矩阵中，局中人是理智的，为了降低成本，增加预算剩余，决策者R会在最少赢得中选择一个最大赢得，即：

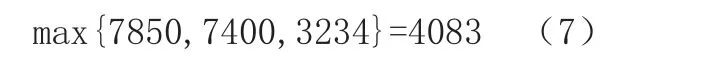
对于局中人B即客观条件来说：

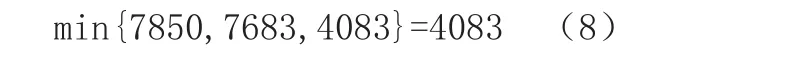
由（1）式可得VG=4083为最优解，存在于方案b1中，即b1为最优方案。该系为了降低成本，增加预算剩余资金，降低因材料不足造成的增加成本的风险，b1方案是最优的选择。选择b1方案，能够保证成本在预算之内，同时剩余资金最少不会少于3234元。

从赢得矩阵中，可以看出存在剩余资金7850元的方案，但是这样也可能面临剩余资金低至3234元的风险。因此，从理智的行为选择中找到最优的方案b1，并可以依据这个方案制订宣传资料制作的计划。

3 结语

通过案例分析，运用决策论找出实施的最佳方案，降低了成本，解决了高校工作事务中面临的繁杂决策问题。对策论是运筹学的重要分支之一，从个人日常生活、工作到国家的政治、经济、军事、科研等领域，无一不存在决策问题。有关国家大政方针的决策更为重要，它直接影响到国家的发展、民族的兴衰［3］。因此应该熟练掌握决策论，并善于将决策论与实际生活相联系，应用到工作生活中去，从而获取更加便捷的方法和途径。

［1］李慧.教育装备运筹规划［M］.北京：北京大学出版社，2010：100-116.

［2］徐家旺，王晓波.实用管理运筹学实践教程［M］.北京：清华大学出版社，2014：138.

［3］王玉英.优化与决策［M］.西安：西安交通大学出版社，2014：169.

Scheme Selection based on Game Theory: Make Plan of Making Publicity Material as Example

WANG Shaoqing， LI Hui

In universities， working things， we are often faced with the questions which need us to make the best decision to reduce costs in order to keep the budget. Based on the example of making publicity materials in department of Education Technology， this article is aimed at to choose the best scheme according to the different situations which include a few programs and the using of diff erent materials.

game theory； won matrix； matrix games

G652

B

1671-489X（2016）18-0055-03

10.3969/j.issn.1671-489X.2016.18.055