再谈多解性教学在向量复习中的有效性

筅江苏省连云港市新浦中学　史晓伟

再谈多解性教学在向量复习中的有效性

筅江苏省连云港市新浦中学史晓伟

众所周知，一题多解是中学数学的优良传统.从新课程教学来看，以往的一题多解仅仅是对于问题的一个多角度解答，是从不同的方向、不同的思路去审视分析同一题中的数量关系，从而用不同的方法得到相同的结果.在复习中适当地进行一题多解的训练可以激发学生的创造激情，加深对已学知识的巩固，训练数学思想和数学方法的娴熟运用，锻炼思维的广阔性、深刻性、灵活性及创造性.今天多解性教学是在此基础上的一个挖掘和提高，其更注重了解答过程中所使用的基本知识和基本技能，还囊括了所涉及的数学思想方法，多解性教学更是在复习教学中对于所涉及的知识整体性角度做出一些分析，并从教师教的角度对知识进行了渗透，从学生学的角度进行了整合.用一句话概括，多解性教学不仅涉及问题的过程与方法，更注重了知识背后的思想方法和知识间的联系，进而成为提升复习教学有效性的重要教学方式.

一、知识整合的角度

多解性教学不仅仅是思考多种解决问题的角度，更要思考这些知识间的联系，为什么试题背后常常使用这些基本知识和基本技能？比如，在高三复习中，很多问题类似，做很多次，学生还是做错或者不会做？这是为何呢？学生总说：我忘记了方法.那么，这忘记的背后原因是什么呢？从基本问题的角度来说，笔者认为知识整合性不足是学生对于问题缺少多角度思考的重要因素.因此，复习教学中关注多解性在知识整合角度的渗透是提高问题解决能力的一个关键.

A.组成锐角三角形B.组成直角三角形

C.组成钝角三角形D.在同一条直线上

分析：这是一道情境新颖、知识错综交汇、思维入口开阔、值得研究的问题.

思路1：数量积问题自然应该从知识最基本的角度出发——从向量数量积出发.

解法1：设BBBC·CBBA=3t，CBBA·ABBB=4t，ABBB·BBBC=5t，得-a· bcosC=3t，-b·ccosA=4t，-c·acosB=5t，即a2+b2-c2=-6t，b2+ c2-a2=-8t，a2+c2-b2=-10t，解得a2=-8t，b2=-7t，c2=-9t，其中t<0，由余弦定理得cosC<0，即这三点可以组成锐角三角形.

点评：本方法是同学们的首选方法，利用数量积、余弦定理及方程的思想，体现转化化归思想.

思路2：数量积是中学向量运算最高的级别，高级别的运算是向量最基础运算——向量和差运算的积累，从这里整合入手.

点评：本解法通过向量的和差运算实现三角形三边比例关系，明显较解法1运算少得多，并通过余弦定理实现知识体系纵横联系.

思路3：在头脑中的知识若仅仅能正向运用，那么对于问题的思考力度还是缺乏辩证哲学思想的，要提高复习教学的有效性，更需要从“正难则反易”的哲学角度思考，从特殊情况进行排除，选择题还是灵活机动地用特殊值检验或排除.

若是直角三角形，则必有一个为0，不合题意，排除B；若是钝角三角形，则比例系数一正两负，不合题意，排除C；若是三点共线，则数量积的值不同号，排除D；所以选择A.

思路4：对于本题多解性思考的另外一个角度，则是向量数量积与三角形面积公式中的元素比较接近，从这一知识整合角度出发，从向量结合面积公式，自然有点悠然见南山的感觉.

解法4：不难发现，S△ABC=absinC=bcsinA=casinB，所以=3t，所以tanC=-

所以tanA、tanB、tanC都是正数，即这三点可以组成锐角三角形.

点评：本解法利用向量的数量积的概念，能联想到三角形面积公式，化去边用角来确定三角形形状，不失为好方法.

多解性整合的再思考：从上述问题解决的角度来说，将数量积知识整合在不同的解答中，有效地整合了向量相关的各种基本知识，这些知识的横向思考和纵向运用，大大加强了学生对于知识运用的能力，笔者认为对于有效的试题还需要进一步从多解性教学中加强思考的眼光.

二、后续思考的角度

从上述的不同四种解法，不难得到以下问题推广：

点评：向量是新课标中的必修内容.由于向量具有数与形的双重性，也使得向量与教材其他内容相比，更具独特性.正是由于向量的上述特征，高考命题者对向量内容格外青睐，在命制有关向量问题时，呈现形式鲜活，知识纵横交汇，可谓匠心独具，从而使得向量试题成为高考试卷中一道亮丽的风景.因此，向量复习教学追求的是高效率的复习方法，就是做尽量少的题，复习尽量多的基础知识，因此在做一道题时要尽量用各种不同的基础知识去求解，也就是用一题训练多个知识点，由一题掌握多法，利用一个问题发散知识的广度，提高知识运用的整合性，从而获得事半功倍的效果.

三、思想方法的角度

多解性教学并不只是解决单一的问题，而是要从典型问题的解决中寻求知识背后涉及的本质和思想方法，唯有更有深度的挖掘，才能使得多解性教学有别于以往的一题多解，才能在思想认识的深刻性上有更多的启发.

问题2：已知a·b=0，向量c满足（c-a）·（c-b）=0，|ab|=5，|a-c|=3，则a·c的最大值为________.

解法1：（图形化思想）设|a|=a，|c|=c，则由已知条件a·b=0，（c-a）·（c-b）=0，如图1，易得Rt△ABC和Rt△OAB中，∠AOB=∠ACB=90°且O、A、C、B四点共圆，圆的直径就是5，又由圆的性质可设∠AOC=∠ABC=θ，在Rt△ABC中，cosθ=，则在△OAC中，由余弦定理及基本不等式得32=|AC|2=a2+c2-2accosθ≥2ac-2ac×ac，所以ac≤，所以a·c=a·c·cosθ≤=18.

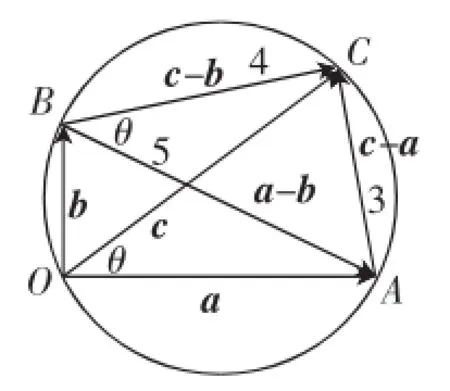
图1　

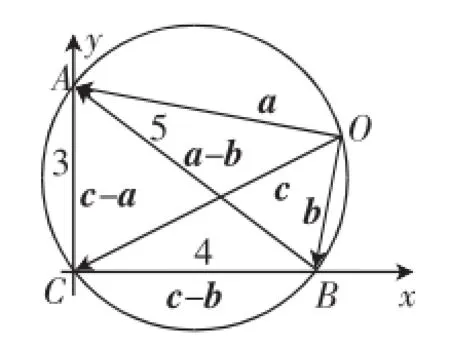
图2　

解法2：（代数化思想）以C为坐标原点，以CA为y轴，以CB为x轴建立平面直角坐标系，如图2，易得A（0，3）、B（4，0），设O（x，y），则a=（-x，3-y），b=（4-x，-y），c=（-x，-y），因为a·b=-4x+x2-3y+y2=0，即y2-3y=4x-x2，所以a·c= x2+y2-3y=x2+4x-x2=4x.而O（x，y）的横坐标x的取值范围为≤，所以4x∈［-2，18］，从而a·c的最大值为18.

点评：代数思想和几何思想解向量问题本身就是向量自身特点决定的，学生在向量问题中的困扰一直存在，其认为向量问题往往灵活性强、难度大，殊不知从思想方法的角度来说，唯有两种常规思想的介入，即几何图形化思想和代数运算的力量，只要选择合理的角度去尝试，久而久之势必会在向量问题解决的经验上有更多的积累.

问题3：设e1，e2为单位向量，非零向量b=xe1+ye2，x， y∈R，若e1，e2的夹角为的最大值等于________.

解法1：（图形化思想）不妨设x≠0，由b=xe1+ye2，x， y∈R，则

点评：两种不同的方式解决向量问题，我们发现利用图形化，掌握图形变化的本质，数形结合，直观而简洁，利用代数法是从函数入手，通过相关运算得到一个二元函数，然后换元转换为一元函数求解最值.相比而言，思想方法的结合，使得问题的走向脉络清晰，通俗易懂.

总之，纵观高中数学，很多知识之间存在联系，对典型例题解法的总结、回味与“提炼”，变重解题的数量为重解题的质量和解题后的反思.力求做到吃透一道题，掌握一类题，悟出一些方法、道理，从题海中解放出来.总之，我们高三复习应倡导多解性教学，作为一线的老师就要适当选好题组，选好解题方向，起到“授人以渔”的作用.作为中学数学教师，多一点观察生活、多一点读书思考，使得数学教学与时俱进，教学中少点儿“命令式”，多点儿“探究式”；少点儿强硬灌输，多点儿数学欣赏，不仅使教师自身积累美的涵养，也产生良好的教学效果，使课堂具备生命力.教师重视在数学知识和数学思想方法间讨论联系、揭示数学知识本质，学生就会少一些困惑和惊奇，有利于帮助他们看透问题，多角度地思考问题，正所谓“漫江碧透，鱼翔浅底”！

1.章建跃.理解学生理解数学理解教学［J］.中国数学教育（高中版），2010（12）.

2.康宇，马跃进.赏析2011年高考精彩向量题［J］.数学通讯，2011（9）.F

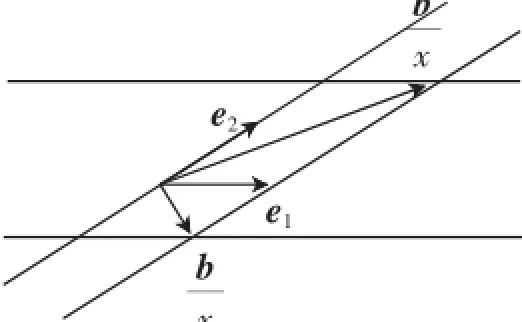
图3