概念图教学在高中数学中的应用研究

郭慧婷

高中数学内容多且抽象，孤立地理解与学习，效率不高。而概念图教学可以形象地展示知识结构与内在关联，帮助学生抓住知识本质，建构知识网络，提高学习效果。

一、利用概念图。深化概念理解

在高中数学概念学习中，借助数学概念图，能形象而直观地展示知识层次结构，引导学生自主建构数学概念认知结构，有效梳理知识间的关联，帮助他们多层次、多方面地理解与把握数学概念。在高中数学教学中，教师可以适当地运用数学概念图讲解教学内容，以图解形式构建知识体系，帮助学生深化理解与记忆。

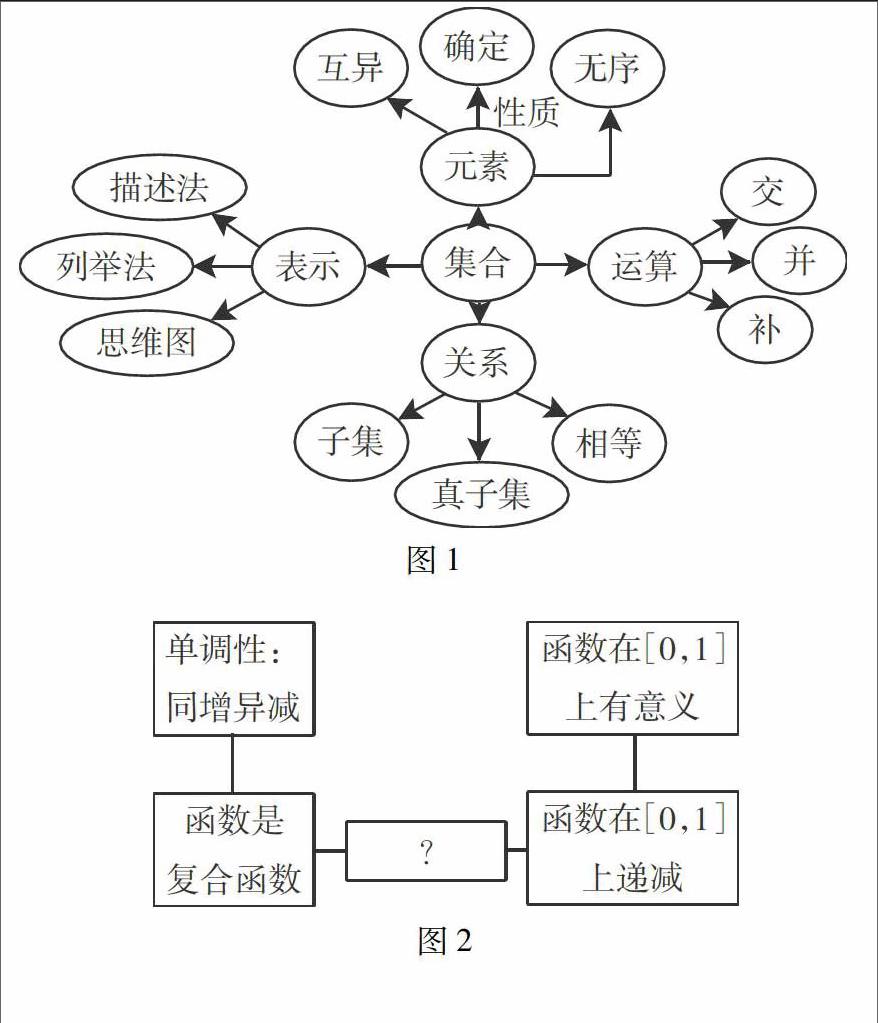
例如，在讲“集合”时，内容既包含了集合、子集、并集等概念，也含有集合性质、集合关系与运算等知识点。为促进学生对集合概念的理解，数学教师可将相关概念及其关系进行有机串联与高度浓缩，形成如图1所示的概念图，就能直观扼要地呈现出集合的性质、集合的运算与方法以及集合相互关系等知识点，让学生一目了然。这样，既有助于学生加深概念理解，把握概念实质，还能够助其形成系统的知识结构，整体把握学习内容，从而更好地迁移与运用。

二、运用概念图。巩固知识记忆

在高中数学教学中，教师不仅要教授预设的教学内容，还要适时引导学生总结与回顾课堂所学，以便巩固知识记忆。借助数学概念图，可以将零散的概念或知识点整合起来，便于再次回顾与复习，帮助学生更好地消化与巩固课堂所学知识。在教学中，教师可以借助概念图总结教学重点，突出知识难点，便于学生课后整理与记忆。

在数学教学中，教师可以引导学生补充自己故意留白的概念图，或者让学生动手尝试绘制有关概念图，给学生创造更多的自主学习与深入思考的空间，让学处主动梳理知识点的内在联系与区别，使之概括化、网络化。

例如，复习课教学，教师可以活用概念图的方式，指导学生根据概念（知识）之间的异同与内在联系，将前后所学内容进行整理与概括，形成个性化的概念图，实现知识的迁移、重建与拓展，提高学生的梳理与建构能力。

三、借助概念图。优化数学解题

在数学学习中，要成功解决数学问题，学生就需要具备较强的思考分析能力，掌握一定的解题方法，明确解题思路。其中，概念图是一种有效的解题工具与方法，可揭示题设与问题、问题与问题的紧密关系，有助于学生探寻已知条件与隐含条件的内在联系，弄清问题实质，找到解题的关键点，获得正确的解题思路。

例如，现有函数f（x）=log_a（2-ax），已知它在区间[0，1]内是减函数。请求出a的取值范围。尽管题中所给的已知条件并不多，但函数的真数与底数中都有参数a，即便展开分类讨论，若想获得正确结果也有一定难度。此时，教师可借助已知条件与所求问题的概念图（如图2）进行讲解分析，指导学生思考探索，获得有效的解题思路与方法。

数学教师可引导学生列出已知条件，如题中所给函数是μ=2-ax与f（x）=log_aμ组成的复合函数，其定义域是[0，1]，并且是减函数。接着，要求学生结合概念图分析复合函数的单调递减条件、同增异减性、定义域间的关系。如此，学生就能快速联想到运用复合函数的单调性解决问题。这样，将概念图与数学习题进行巧妙结合，使解题中的整体思维过程变得可视化，题中隐含信息也明显地展示出来，便于学生更好地理解，提升了解题效果。而后教师提供类似习题，引导学生自绘概念图解题，使其再次主动思考，学会触类旁通，做到举一反三，从而提高处理信息、解决问题的能力。

总之，在高中数学教学中，概念图是一种行之有效的教学策略与辅助手段，教师可根据教学实际灵活运用，提高学生的学习效果。