从两个教学片断审视课堂生成

蔡友山

摘要：在初中数学教学中，教师不拘泥于预设，并能智慧地处理好预设与生成的关系，生成才能更加精彩，才能使数学课堂更具有活力，才能使课堂教学效率达到最大值。在初中数学教学中，教师要注重知识的形成过程，善于利用问题引发学生的数学思考，鼓励学生的创造性思维，充分体现学生的主体地位，真正实现学生的学与教师的教的统一。

关键词：教学片段 教学预设 课堂生成精彩 积淀

在初中数学教学中，教师处理好预设与生成的关系，是提高课堂教学效益的关键所在。教学过程的生成性对教学预设提出了更高的要求。每位教师只有创造性地使用教材、全面地了解学生和有效地开发课程资源，预设才能富有成效。同时，在初中数学教学中，教师只有不拘泥于预设，并能智慧地处理好预设与生成的关系，生成才能更加精彩，才能使数学课堂更具有活力，课堂教学效率才能达到最大值。

一、自然生成。成就课堂精彩

对于浙教版（七上）教材“7。7相交线”，在教学时，我对例1做了如下改动：

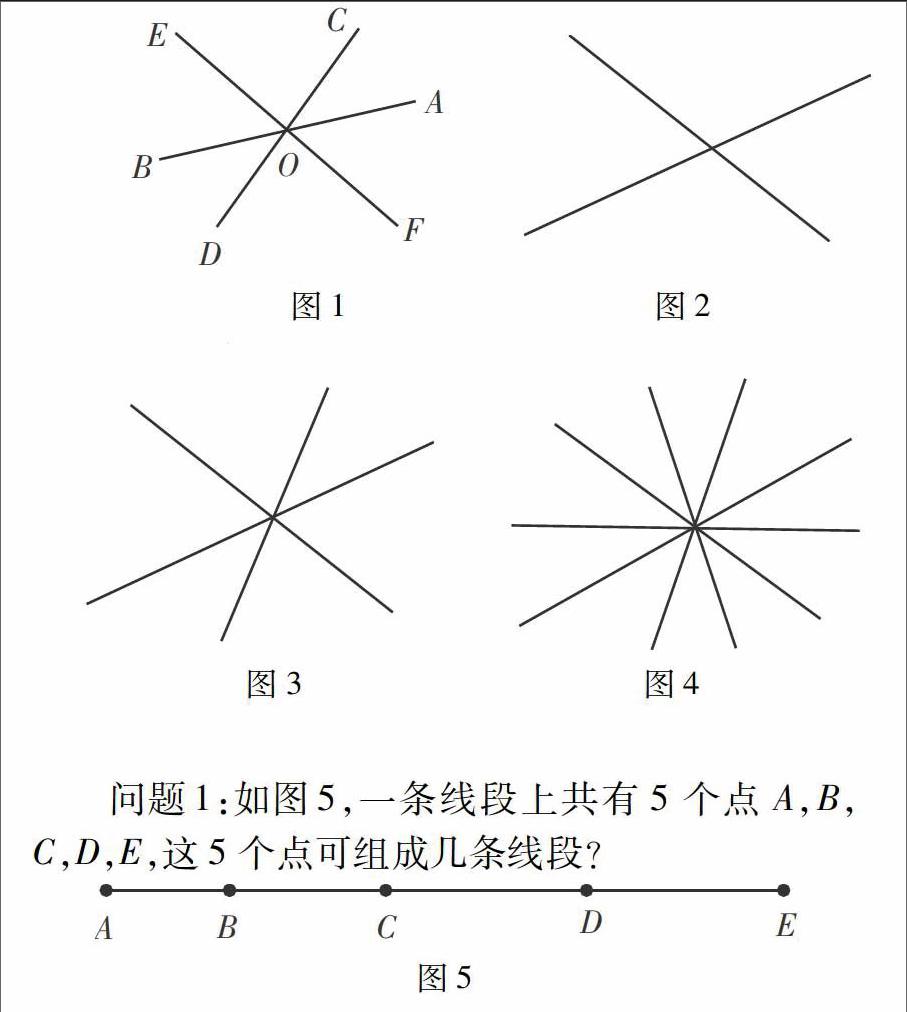
原题：如图1（原图7—37），3条直线相交于一点O，说出图中的6组对顶角。

改动：如图1，3条直线相交于一点O，图中有几组对顶角？

改动意图：解题目标的变化，势必导致解题思维方式的变化。前者目标是“找6组对顶角”，侧重点停留在“找”，且有数量“6”的限制。学生解决问题的思路具有明确的导向性，不利于学生思维的发散。相反，后者为学生提供了更加广阔的思维空间。

教学片段1：

学生A：有4组。

学生B：不对，有5组。

学生C：应为6组。

教师：还有其他结果吗？请这3个同学讲讲自己的理由。

A同学走上讲台用不同颜色的粉笔画出4组对顶角。

台下很多同学：还漏掉了2组。

教师：谁上来画出漏掉的2组。

学生D走上讲台画出漏掉的2组。

教师：看来，数图形的个数需要仔细认真，力求做到不重不漏。

学生E：我有更简单的方法确定对顶角的组数。

教师：我们用热烈的掌声请E同学上台发表高见。

学生E：如图2，两条相交直线，我们称之为一个基本图形，其中有2组对顶角。如图3，因为图中任何两条直线都构成一个新的基本图形，根据“二合一原理”，构成基本图形的总个数为2×3=6。由此可知，其中有2×3=6组对顶角。（师生惊讶，并给予长时间热烈的掌声）

教师：E同学解法新颖，讲解清楚明了，值得大家学习。用此法，不用一一画出这些对顶角。只要知道直线的条数，就容易计算出对顶角的组数。

教师：请同学们用E同学的方法分组讨论两个问题：（1）如图4，5条直线相交于同一点，其中包含几个基本图形？有几组对顶角？（2）n条直线相交于一点，其中包含几个基本图形，有几组对顶角。（分组讨论5分钟左右）

教师：请同学们分组展示讨论结果。（每组派一个代表发言）……

二、精彩的生成。源自课堂积淀

您读到这里，难免会产生一丝困惑：学生E为什么会有如此奇妙的解法？“二合一原理”又是什么新鲜事物？下面的教学片断或许能为您揭开谜底。（说明：片断2是在片断1之前的一节习题课）

教学片段2：

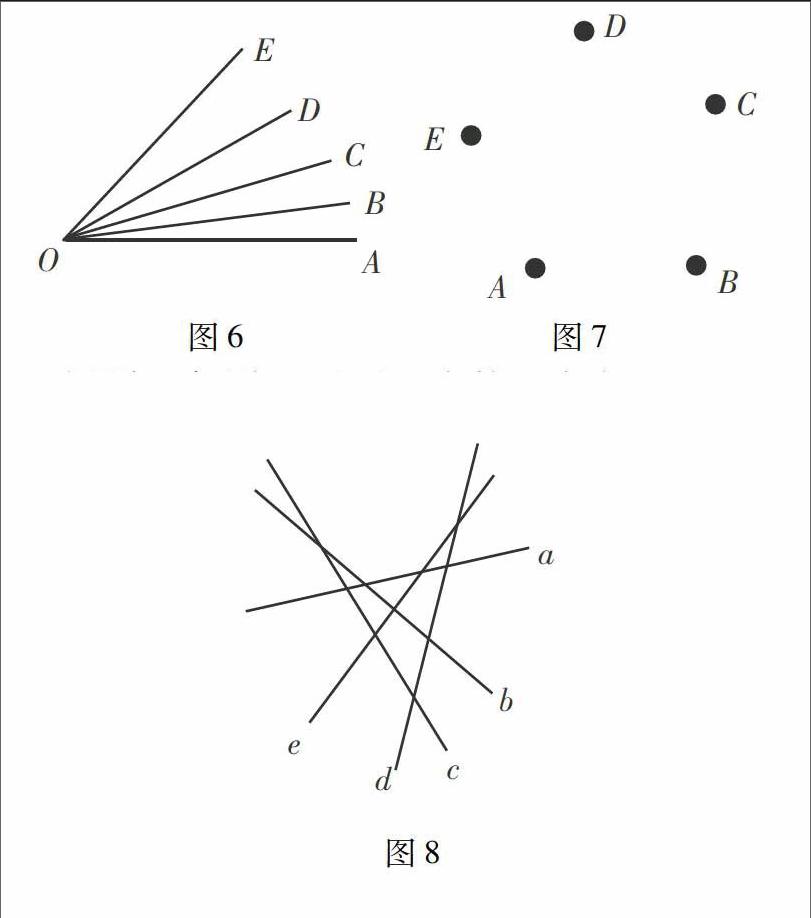
问题1：如图5，一条线段上共有5个点A，B，C，D，E，这5个点可组成几条线段？

学生A：10条。

教师：能说说你的理由吗？

学生A：以A为端点的线段有：AB，AC，AD，AE，共4条；以日为端点的线段还有：BC，BD，BE，共3条；以C为端点的线段还有：CD，CE，共2条；以，D为端点的线段还有：DE，1条。所以，共有线段4+3+2+1=10（条）。

教师：以B为端点的线段不是还有BA吗，你为什么没有把它算进去？

学生A：因为线段AB与线段BA是同一条线段，不能重复计数。

教师：说得好！在分类计数时，我们一定要做到不漏不重。

教师：刚才这位同学用枚举法把所有线段都一一列举出来，这是解决计数问题的一种好方法。还有其他方法解决这个问题吗？

学生B：因为以A为一个端点的线段有4条，同样以B，C，D，E为一个端点的线段都有4条，因此线段的总条数为4×5，但每条线段都重复计数一次，所以线段的总条数为1/2×4×5=10。

教师：这种方法很有新意，而且非常简捷。现在请大家选择一种方法解决下面的问题。

问题2：如图6，从同一端点O出发的5条射线OA，OB，OC，OD，OE，可组成几个角？

问题3：如图7，过平面内的5个点A，B，C，D，E，最多可画几条直线？

问题4：如图8，平面内有5条直线a，c，d，e，它们最多有几个交点？

学生：独立完成，选代表展示。（结果都是4+3+2+1=10）

教师：它们的结果为何如此相似？你能否从这4个问题的本质上进行分析说明？（提示：这4个问题有什么共同点？）

经过教师的提示，学生七嘴八舌地说开了，教师把同学们的想法进行提炼板书：

问题1：任意两点构成一条新的线段。

问题2：任意两条射线组成一个新的角。

问题3：任意两点构成一条新的直线。

问题4：任意两条直线产生一个新的交点。

教师：我们发现，这4个问题有着共同的特征，不妨归纳为：对于n个元素，如果其中任意两个元素都能构成一个新元素，那么构成新元素的总个数为（n-1）+（n-2）+…+2+1=1/2（n-1）n（个）。

学生：原来如此。

教师：为了方便记忆，我们不妨称之为“二合一原理”。你能举出一些生活中的“二合一”问题吗？

学生：握手问题，单循环赛问题，等等。

三、反思

1.合理利用生成性资源，提高课堂教学的有效性

教学方案是教师对教学过程的预设，实施教学方案，是把预设转化为实际的教学活动。在这个过程中，师生双方的互动往往会生成一些新的教学资源，如新情境、新问题、新思路、新方法、新结果等。这就需要教师能够及时把握，因势利导，适时调整预案，使教学活动达到更好的效果。正如片断1，学生E提出了与众不同的解决问题的新方法，这显然超出了教师的预设，但教师及时捕捉了这一思维火花，并把它转化成生成性资源，通过教师的肯定、总结，学生的强化训练，把这一资源的作用发挥到极致，提高了课堂教学效率。这就是教师的智慧，也是教师追求的教学境界。

2.整合多元知识，为课堂生成提供原动力

片断2是一节习题课，教师没有就题讲题，而是把同类问题罗列出来，让学生经过观察、比较，发现它们的共同特征，从本质上弄清了“它们的结果为何如此相似？”不仅如此，教师还创造性地总结出“二合一原理”，实现了多元知识的整合，使原本零散的知识点得到“归一”，这是中国古代教学思想“由博返约”的体现。在这个过程中，教师十分注重知识的形成过程，善于利用问题引发学生的数学思考，鼓励学生的创造性思维，充分体现了学生的主体地位，真正实现了学生的学与教师的教的统一。也正因为片断2的积淀，才会出现片断1的精彩，这是知识的迁移，更是能力的提升。