不同隧道位移边界和土体损失对上卧管线的影响

余景良,孙廉威,晁春峰

(1.广州航海学院 航务工程学院,广东 广州 510725; 2.浙江大学 建筑工程学院,浙江 杭州 310058; 3.浙江省交通运输科学研究院,浙江 杭州 310006; 4.桥梁无损检测与工程计算四川省高校重点实验室,四川 自贡 643000)



不同隧道位移边界和土体损失对上卧管线的影响

余景良1,孙廉威2,晁春峰3,4

(1.广州航海学院 航务工程学院,广东 广州 510725; 2.浙江大学 建筑工程学院,浙江 杭州 310058; 3.浙江省交通运输科学研究院,浙江 杭州 310006; 4.桥梁无损检测与工程计算四川省高校重点实验室,四川 自贡 643000)

盾构隧道掘进对地表以及构筑物的影响主要是由掘进过程中土体损失引起的。前人在地铁盾构隧道开挖对地下管线的影响分析大多是基于三维的隧道开挖模型,隧道开挖引起的土体损失采用强度折减法或者假定一定的土体受损率。文章基于Park提出的隧道周边4种径向位移边界条件,以某实际工程为例建立二维隧道与管线的相互作用模型,讨论不同位移边界条件以及不同土体损失情况下,隧道开挖对管线的影响,对椭圆化位移边界条件和均匀位移边界条件进行比较分析。结果表明,椭圆化位移边界条件更接近实际,同时为了保证上部构筑物的安全,盾构掘进时土体损失率尽量控制在0.5%以内,并且可以对管线进行适当的注浆。

盾构隧道;地下管线;二维模型;有限元;数值模拟

随着城市的快速发展,地面交通已不能满足人们出行的需求,越来越多的城市开始规划和修建城市轨道交通。地铁作为轨道交通的核心组成部分,受到越来越多城市的青睐。然而地铁的修建不可避免地要穿越一些城市已有的地下建筑设施和地下管线,包括隧道、桩基、地下商城等地下设施以及给排水、煤气、电信、热力及有线电视等城市地下管线。在地铁盾构掘进过程中保护好这些已有的建筑设施和地下管线已成为地铁施工安全中的难点和重点。

前人主要采用数值模拟的方法对地铁隧道穿越地下结构的影响进行研究。文献[1]基于ANSYS软件对隧道与管线之间的相互作用进行分析，并与离心模型试验结果进行了对比,发现有较好的吻合;文献[2-4]基于ABAQUS软件分析了基坑以及隧道开挖对管线的影响,并与实测结果进行了对比;文献[5-9]基于FLAC3D有限差分软件对多种类型的管线(如双线隧道下穿管线、考虑流固耦合等情况)进行了分析。以上研究对盾构开挖下穿地下结构物的问题进行了一定分析,并对不同地下结构物、地下结构物与隧道距离等因素进行了参数敏感性分析。实际上,盾构隧道掘进过程中,引起地下结构物沉降的主要因素是掘进过程中的土体损失。文献[10]利用现场监测的方法对盾构隧道开挖对地下管线变形的影响进行了分析和研究，提出了管线变形和破坏的监控值。文献[11]将盾尾空隙的大小、注浆充填的程度、隧道壁面土体受扰动的程度和范围等对地层位移有着重要影响的因素概化为一均质、等厚、弹性的等代层,使得用等代层替换衬砌周围实际的土层及注浆情况后地表变形保持不变。这些研究成果中地铁盾构隧道开挖对地下管线的影响大多是基于三维的隧道开挖模型,隧道开挖引起的土体损失采用强度折减法或者假定一定的土体受损率。文献[12]简化出了隧道周边4种径向位移边界条件，在均匀位移边界条件下又扩展出了3种椭圆化位移边界条件以更加符合实际。文献[13]采用复变函数分析4种不同位移边界条件下隧道施工引起的地基变形,但是该方法的适用性是有限的,土体要是均一的土质,不能是分层土,不能分析对其他构筑物的影响。因此有必要将理论计算的隧道位移边界应用到数值分析中。

本文基于某隧道下穿管线的实体工程,通过采用有限元方法,利用隧道周边4种径向位移边界条件[12],假定不同土体损失率,来模拟计算分析不同盾构隧道位移边界条件和土体损失对上卧管线的影响。

1 有限元模型及参数选取

1.1 工程简介

本工程为地铁区间双线盾构隧道项目。隧道内径为5.5 m,外径为6.2 m,隧道间距为26.2 m。底部距离地表15.7 m。在区间垂直下穿1根排水管道,排水管道为钢管,排水管管径为2 200 mm,管底距离地表为6.9 m。

1.2 有限元模型

考虑到隧道垂直下穿管线,且在盾构穿越管线正下方时对管线影响最大,因此本文将模型简化为二维平面应变问题。考虑到边界条件的影响,模型在平面内长150 m,垂直方向取30 m。管线则采用梁单元进行模拟,长度为150 m。有限元模型如图1所示。土体采用摩尔库伦模型,参数见表1所列,管道采用弹性模型,其重度为78.5 kN/m3,弹性模量为206 GPa,泊松比为0.3。

图1 有限元计算模型

土体名称重度/(kN·m-3)弹性模量/MPa泊松比黏聚力/kPa内摩擦角/(°)厚度/m粉质砂土18.512.400.284.1227.30砂质粉土夹粉砂18.813.800.2615.21712.05淤泥质粉质黏土17.43.050.3827.91910.65

管道与土体之间采用embedded接触方式,相当于把管道嵌入到土体中,位移协调变形。整体模型在底部边界施加y方向约束,在左右边界施加x方向约束。

1.3 隧道位移边界条件的确定

1.3.1 土体损失的定义

关于土体损失有以下3种定义:

(1) 径向收缩[14]表达式为:

(2) 土体单元损失[15]表达式为:

(3) 等效土体损失[16]表达式为:

第1种模型在计算土体损失率时比实际偏小,因此第2种和第3种模型更为合理；而在本文计算中,第2种模型中的u0能更好地与后面不同隧道位移边界条件结合起来,因此取土体损失的定义为第2种。

1.3.2 隧道位移边界条件的确定

文献[12]简化出了隧道周边4种径向位移边界条件,具体如图2所示。4种位移边界条件分别为:

其中,ur为隧道周边径向位移;u1、u2、u3、u4的含义如图2所示,r和θ′的含义如图3所示。

图2 4种径向位移边界条件

通过相应的位移场,当ui≪r0时,4种边界条件下,土体的损失分别为:

BC-1:S1=2πr0u1；

BC-2:S2=2πr0u2；

BC-3:S3=3πr0u3/2；

BC-4:S4=7πr0u4/4。

假定4种边界条件下土体的损失相同,则有:

u1=u2=3u3/4=7u4/8。

图3 坐标系统图

文献[13]采用复变函数分析了4种不同位移边界条件下隧道施工引起的地基变形的计算分析结果,认为BC-3最为接近工程实际。

因此本文计算将采用BC-3位移边界条件作为位移荷载施加在地铁盾构隧道上；同时因为在本工程中,根据现场资料,土体的损失率为0.5%左右,所以取BC-1边界条件,计算其土体损失为0.5%时的情况与BC-3作为比对。并假定土体分别为0.5%、1.0%、1.5%、2.0%,r0为隧道外半径取3.1 m,则可以计算出BC-3下的位移边界条件分别为:

n=1,2,3,4。

其中,u31=0.010 3 m;u32=0.020 6 m;u33=0.031 m;u34=0.041 3 m。

同时可以计算出土体损失率为0.5%时,BC-1下的位移边界条件为:

ur(r=r0)=-u1=-0.007 75 m。

2 计算结果分析

在进行双线地铁盾构隧道开挖对管道的受力变形影响分析时,根据施工顺序有3种工况,分别为:

工况1 地应力平衡;

工况2 左线盾构隧道开挖完成(即施加L1线位移边界条件);

工况3 右线盾构隧道开挖完成(即施加L2线位移边界条件)。

2.1 BC-1位移边界条件下的计算结果分析

2.1.1 管道弯矩、剪力及沉降分析

在土层损失率为0.5%时，地铁左线(L1)隧道开挖后引起的管道弯矩图如图4a所示,弯矩最大值为132.3 kN·m,地铁右线(L2)隧道开挖后引起的管道弯矩图如图4b所示,弯矩最大值为100.4 kN·m。

由图4可以看出,当L2线隧道开挖完成后,比L1线隧道开挖完成后管道的最大弯矩有所减小,减小了29.9 kN·m。

图4 隧道开挖后管道弯矩分布图

在土层损失率为0.5%时，地铁左线(L1)隧道开挖后引起的管道剪力图如图5a所示,剪力最大值为15.09 kN,地铁右线(L2)隧道开挖后引起的管道剪力图如图5b所示,剪力最大值为14.51 kN。由图5可以看出,L2线盾构隧道开挖后,比L1线隧道开挖后剪力基本没有变化,只是减小了0.58 kN。

地铁左、右线隧道开挖后引起的管道竖向位移分布如图6所示,左线(L1)隧道开挖后引起最大竖向位移为3.6 mm,右线(L2)隧道开挖后引起的最大竖向位移比L1有所增大,最大值为3.87 mm。

由图6可知,当左线(L1)隧道开挖后,管道的最大沉降发生在左线隧道的正上方,而当右线(L2)隧道开挖后,沉降最大值并没有发生在两隧道的中心位置,这是因为2个隧道相距比较远,右线隧道开挖对左线隧道的影响并不是很大,所以管道的最大沉降位移只是向两隧道中心线的位置偏移了一些。

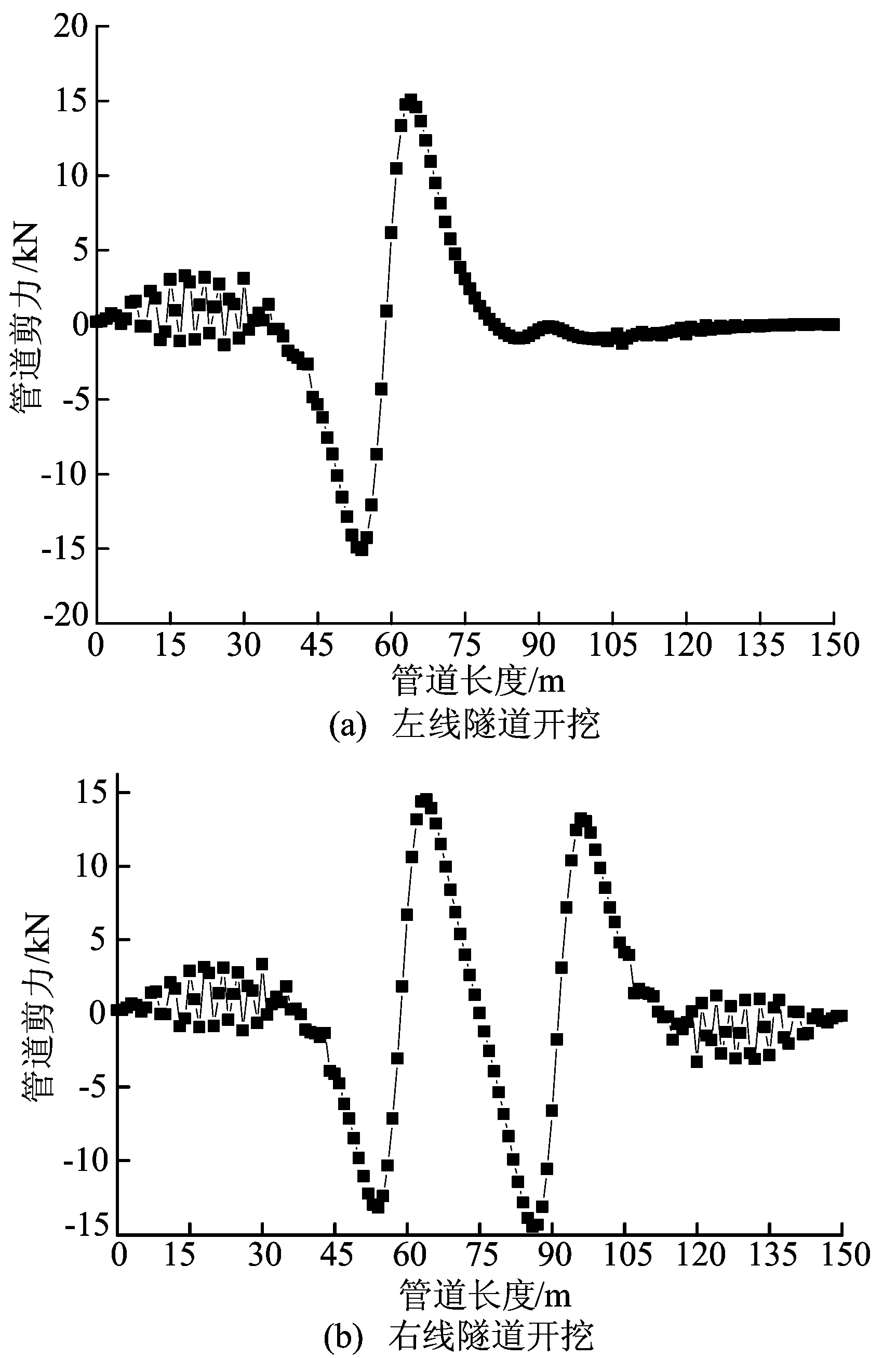
图5 隧道开挖后管道剪力分布图

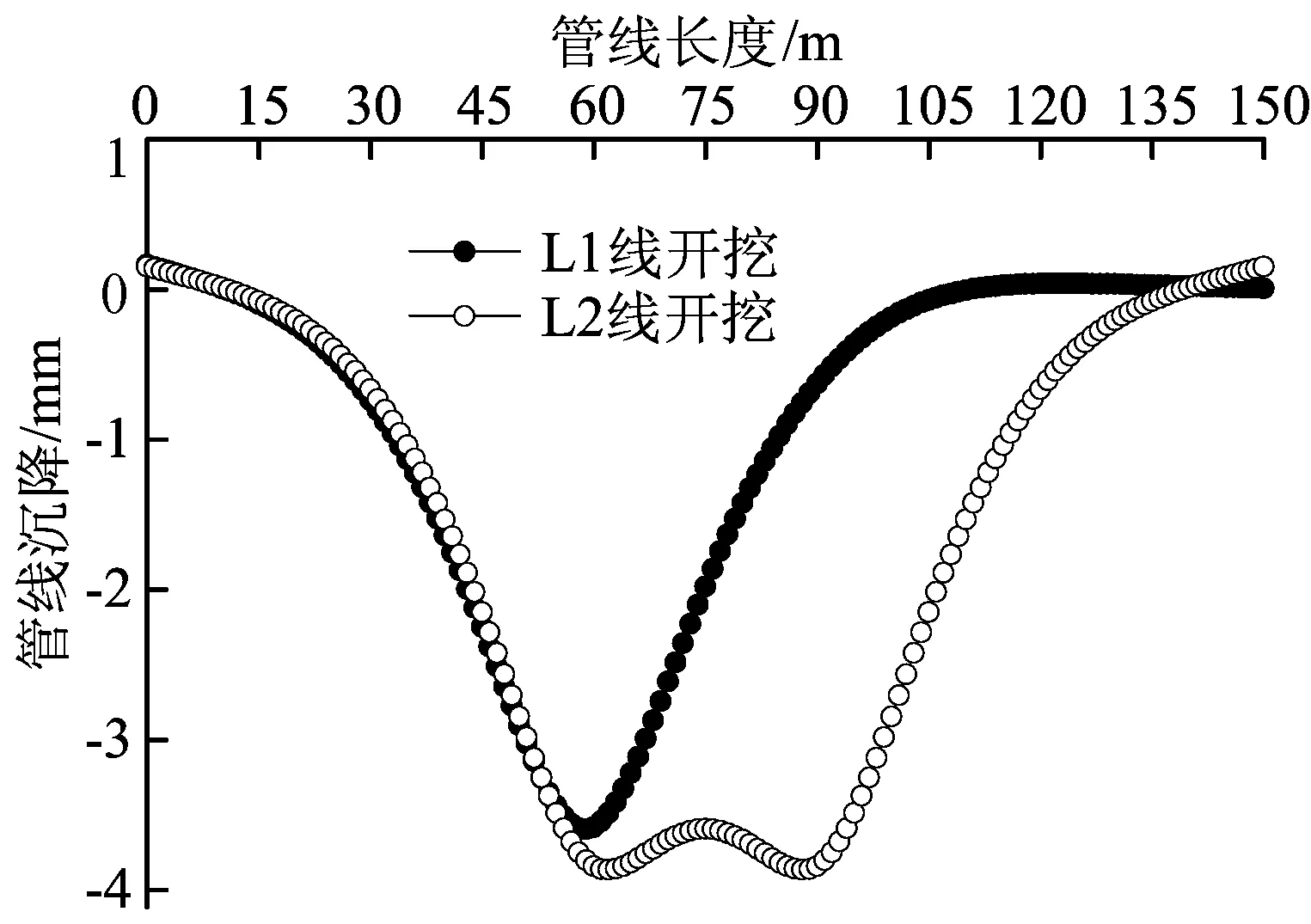
图6 地铁盾构左右线施工对排水管道竖向位移影响

2.1.2 地表沉降分析

地铁左、右线隧道开挖后引起的地表沉降分布如图7所示,左线(L1)隧道开挖后引起最大竖向位移为2.25 mm,右线(L2)隧道开挖后引起的最大竖向位移比L1有所增大,最大值为2.51 mm。

通过对比图6和图7可以发现,地表的沉降规律和管道的沉降规律相似,但是在数值上有所差别,地表沉降要小于管线的沉降。

图7 地铁盾构左右线施工对地表沉降影响

2.2 BC-3位移边界条件下的计算结果分析

2.2.1 管道附加弯矩分析

在不同土体损失率下,地铁左线(L1)隧道开挖后引起的排水管道的弯矩如图8a所示,引起的管道弯矩最大值分别为429.8、858、128 9、171 4.5 kN·m。

在不同土体损失率下,地铁右线(L2)隧道开挖后引起的排水管道的弯矩如图8b所示,引起的管道弯矩最大值分别为325.1、649、975.5、1 297.5 kN·m。

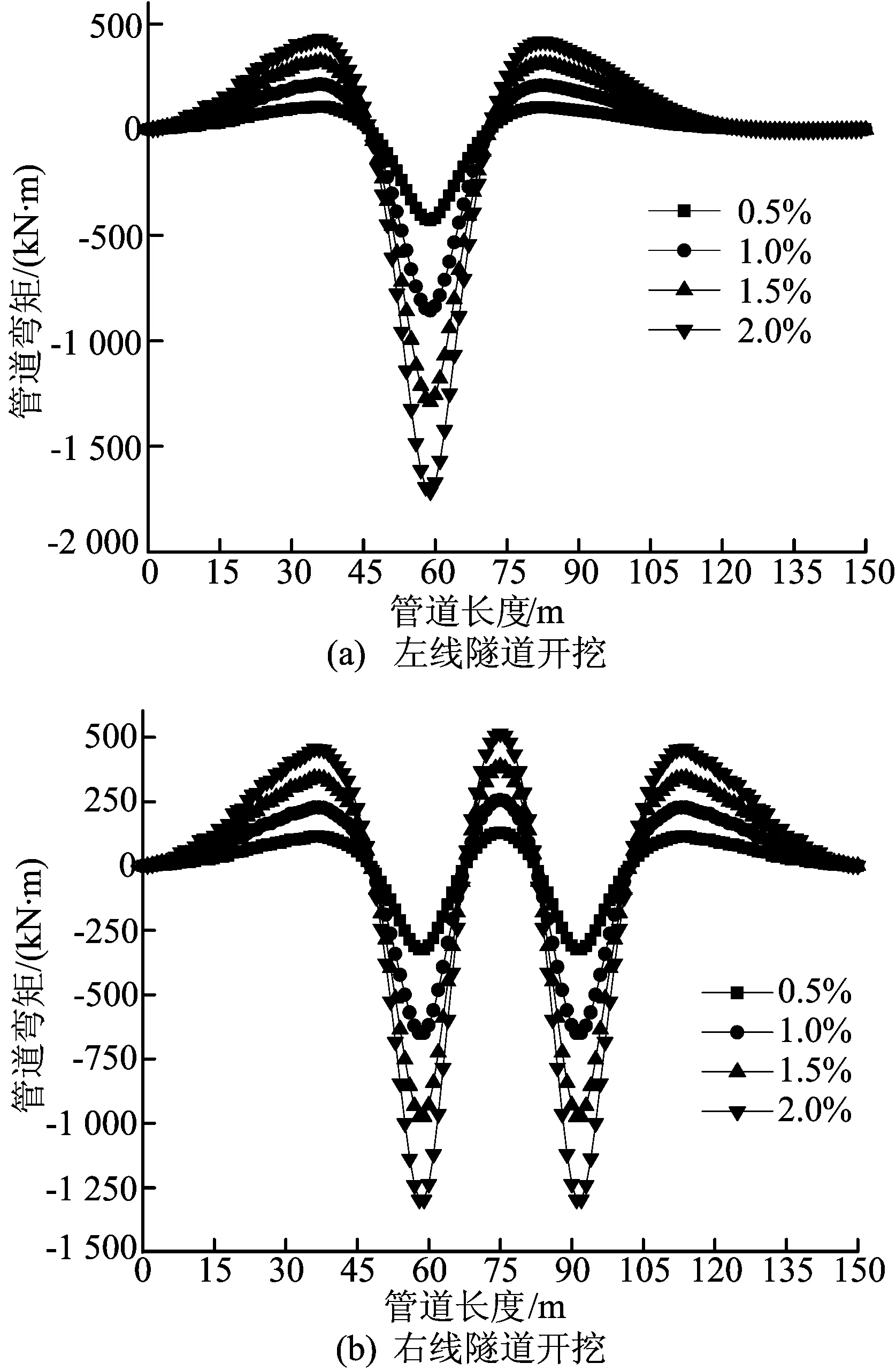
图8 不同土体损失率下管道弯矩分布图

不同土体损失率下,左、右线开挖,排水管道的最大附加弯矩值见表2所列。

表2 不同损失率下管道最大附加弯矩 kN·m

由表2可以看出,随着土体损失率越来越大,管道的最大附加弯矩也越来越大,与土体损失率基本呈正比的趋势。当右线盾构隧道开挖后,比左线隧道开挖后排水管道的最大附加弯矩相比则呈减小的趋势,且随着土体损失率越来越大,附加弯矩减小得也越来越多,分别减小了104.7、209、313.5、417 kN·m。

2.2.2 管道附加剪力分析

在不同土体损失率下,地铁左线(L1)隧道开挖后引起的排水管道的剪力如图9a所示,引起的管道剪力最大值分别为46.63、93.1、139.85、186.05 kN。在不同土体损失率下,地铁右线L2隧道开挖后引起的排水管道的剪力如图9b所示,引起的管道剪力最大值分别为46.92、93.7、140.8、187.3 kN。

图9 不同土体损失率下管道剪力分布图

从图9可以看出,随着土体损失率的增大,管道的最大附加剪力也在增大,且呈线性的趋势,当L2线盾构隧道开挖后,比L1线盾构隧道开挖后排水管道的最大附加剪力相比基本没有变化。

2.2.3 管道沉降分析

在不同土体损失率的情况下,地铁盾构隧道左、右线开挖后引起的管道竖向位移的分布如图10所示,L1线盾构隧道开挖后引起排水管道最大竖向位移分别为1.13、2.261、3.396、4.516 cm,L2线盾构隧道开挖后引起的排水管道的最大竖向位移相比于L1线没有很大的增幅,最大竖向位移值分别为1.19、2.375、3.569、4.746 cm。由图10可知,在地铁盾构隧道L2线开挖后,L1线上方管道的位移比L1线开挖后有所增加。

图10 不同土体损失率下管道沉降曲线

从图10可以看出,不同土体损失率下,排水管道的沉降规律基本一致,当土体损失率为0.5%时,排水管道的最大沉降为1 cm左右,当土体损失率大于0.5%时,排水管道的最大沉降则大于1 cm。同时,从表2可以看出,当土体损失率比较小时,排水管道的附加弯矩比较小,L2线开挖后相对于L1线,排水管道的弯矩的变化比较大,并且随着土体损失率的增加,排水管道弯矩的变化也越来越大。综上可以看出,在地铁盾构隧道施工中,应该尽量控制土体损失率在一个较小值,宜取小于0.5%为佳。

2.2.4 地表沉降分析

不同土体损失率下地表的沉降情况如图11所示,从图11可以看出,不同土体损失率下,地表的沉降规律基本一致,通过对比图11和图10可以发现,地表的沉降规律和管道的沉降规律相似,但是在数值上有所差别,地表沉降要小于管线的沉降。

图11 不同土体损失率下地表沉降曲线

2.3 BC-1位移边界与BC-3位移边界对比分析

BC-1位移边界条件把孔洞周边的均匀变形作为问题的边界条件,而实际隧道变形具有椭圆化性。研究结果表明BC-3位移边界条件更为合理[12,16]。采用BC-1进行计算出的结果比实际偏小,这样的计算方式是偏不安全的。

BC-1位移边界条件和BC-3位移边界条件下,土层损失率为0.5%时管道的沉降曲线的数值计算结果和实测计算结果如图12所示。从图12可以看出,当位移边界条件由BC-1变为BC-3后,管道的沉降规律并没有发生变化,但是管道的沉降值发生了很大的变化,当L1线开挖后,BC-3下的管道沉降比BC-1下的管道沉降要大0.7 cm左右。而当L2线开挖后,BC-3下的管道沉降比BC-1下的管道沉降要大0.8 cm左右。同时可以看出,在BC-3位移边界条件下,管道的沉降与实测更为接近。

BC-1位移边界条件和BC-3位移边界条件下管道的附加弯矩最大值的比较见表3所列。从表3可以看出,BC-3位移边界条件下排水管道的附加弯矩最大值要大于BC-1位移边界条件下的附加弯矩最大值。

通过以上的对比分析,可以看出采用BC-3位移边界条件对土体损失引起的沉降进行模拟分析更为合理,更贴近工程实际,计算所得的结果也是偏安全的。

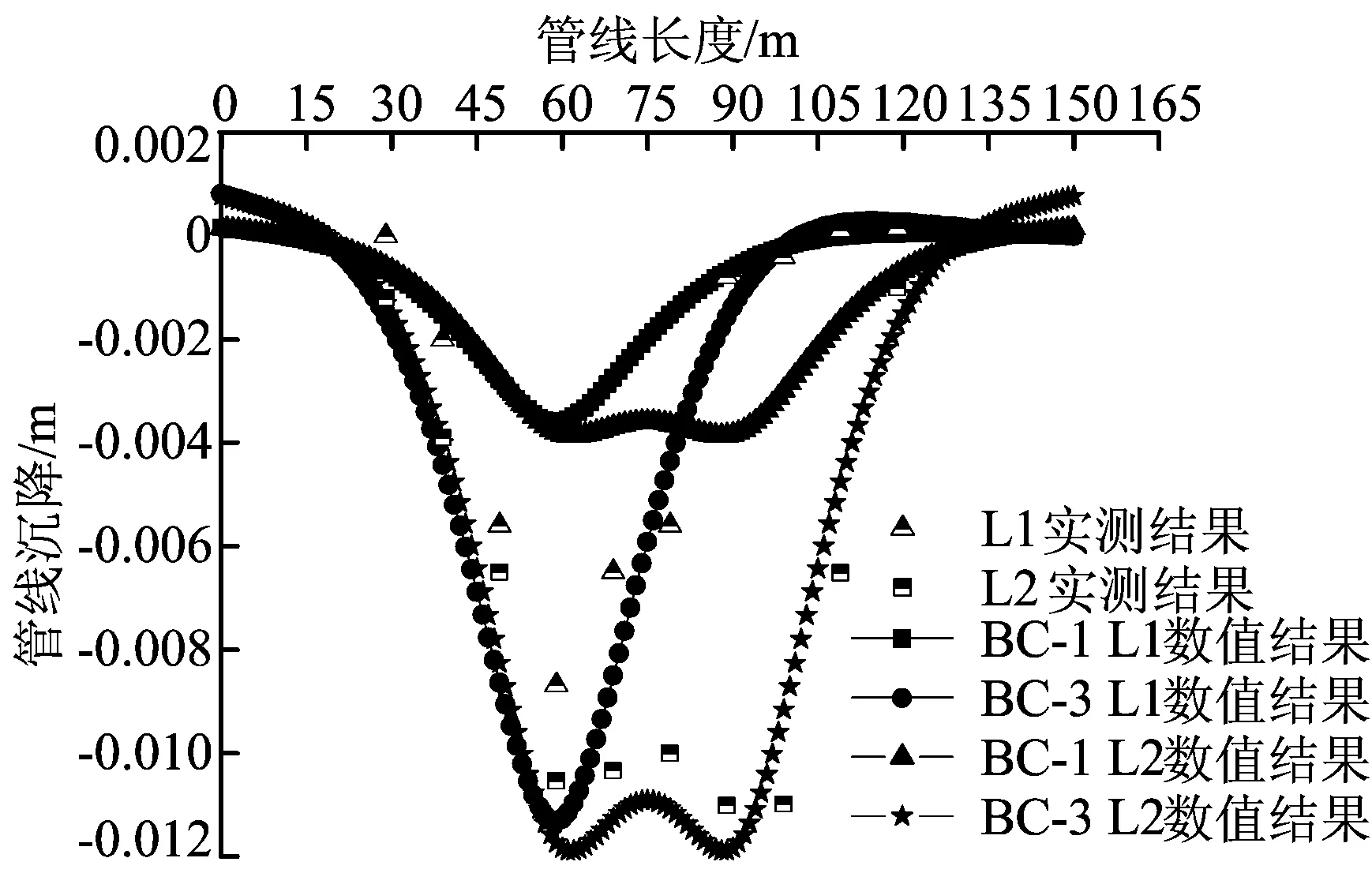
图12 BC-1与BC-3下管道沉降数值与实测结果对比

表3 BC-1与BC-3排水管道最大附加弯矩值 kN·m

2.4 注浆对管道变形的影响

在实际的工程中,为了控制管道在盾构掘进中的变形,往往对管道下部土体进行注浆,从而减小盾构掘进对管道的影响。在以上分析的基础上,取BC-3为隧道位移边界条件,对管道下部0.5 m范围内的土体进行注浆,讨论有无注浆对管道变形的影响。对于注浆层参数的取值参考文献[17],本文注浆层的弹性模量为150 MPa,泊松比为0.25。

在有无注浆2种情况下,管道的沉降曲线如图13所示。从图13可以看出,对管道下部土体注浆可以在一定程度上减小管线的沉降,在本算例中,减小了1/3左右。可见一定的注浆可以有效地控制盾构掘进中上方管线的沉降。

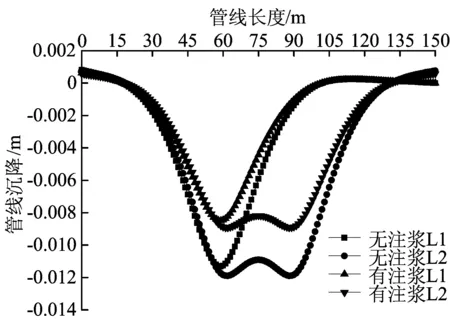
图13 有无注浆情况下管道沉降曲线

3 结 论

本文采用ABAQUS软件分析了地铁盾构隧道左线(L1)和右线(L2)开挖对地下排水管道受力和变形的影响,数值模拟分析结果表明:

(1) 椭圆化位移边界条件比均匀位移边界条件更为合理,更贴近实测的值。

(2) 在椭圆化BC-3位移边界条件下,当土体损失率为0.5%时,地下排水管道的最大沉降为1 cm左右,当土体损失率大于0.5%时,地下排水管道的最大沉降则大于1 cm。

(3) 当L2线开挖后,相对于L1线盾构隧道开挖后的弯矩,管道弯矩值变化比较大,而最大附加剪力基本没有变化。并且随着土体损失率的增加,管道弯矩的变化也越来越大。

(4) 在管线下部进行一定的注浆,可以有效地减小在盾构掘进中管线的沉降。

综上可以看出,在地铁盾构隧道施工中,采用椭圆化位移边界条件比均匀位移边界条件更为合理,同时应该尽量控制土体损失率在一个较小值,宜取小于0.5%为佳,同时辅以管线下部土体一定的注浆,以较好地保护临近的地下管线。

[1] 吴波,高波.地铁区间隧道施工对近邻管线影响的三维数值模拟[J].岩石力学与工程学报,2002,21(增刊2):451-456.

[2] 姜忻良,赵志民,李园.隧道开挖引起土层沉降槽曲线形态的分析与计算[J].岩土力学,2004,25(10):1542-1544.

[3] 毕继红,刘伟,江志峰.隧道开挖对地下管线的影响分析[J].岩土力学,2006,27(8):1317-1321.

[4] 马可栓,丁烈云,李国成,等.武汉越江隧道近邻管线性状的有限元分析[J].华中科技大学学报(城市科学版),2008,25(1):42-46.

[5] 骆建军,张顶立,王梦恕,等.地铁施工对管线的影响[J].中国铁道科学,2006,27(6):124-128.

[6] 吴为义,孙宇坤,张土乔.盾构隧道施工对邻近地下管线影响分析[J].中国铁道科学,2008,29(3):58-62.

[7] 孙宇坤,吴为义,张土乔.既有埋地管道对盾构隧道周围地层沉降的影响分析[J].中国铁道科学,2009,30(3):63-67.

[8] 孙宇坤,吴为义,张土乔.软土地区盾构隧道穿越地下管线引起的管线沉降分析[J].中国铁道科学,2009,30(1):80-85.

[9] 漆泰岳,高波,谭代明.软土地层地铁隧道施工对地下管线的影响[J].西南交通大学学报,2010,45(1):45-53.

[10] 赵文，孙海霞，刘立健，等.地下管线变形与破坏的实验与监测研究[J].合肥工业大学学报(自然科学版)，2009，32(10)：1485-1489.

[11] 张云,殷宗泽,徐永福.盾构法隧道引起的地表变形分析[J].岩石力学与工程学报,2002,21(3):388-392.

[12] PARK K H.Elastical solution for tunneling-induced ground movement in clays[J].International Journal of Geomechanics,2004,4(4):310-318.

[13] 王立忠,吕学金.复变函数分析盾构隧道施工引起的地基变形[J].岩土工程学报,2007,29(3):319-327.

[14] VERRUIJT A,BOOKER J R.Surface settlements due to deformation of a tunnel in an elastic half plane[J].Géotechnique,1996,48(5):709-713.

[15] GONZALEZ C,SAGASETA C.Patterns of soil deformations around tunnels,application to the extension of Madrid Metro[J].Computers and Geotechnics,2001,28(6/7):445-468.

[16] ROWE R K,KACK G J.A theoretical examination of the settlements induced by tunneling:four case histories[J].Canadian Geotechnical Journal,1983,20(2):299-314.

[17] 徐干成,李成学,王后裕,等.地铁盾构隧道下穿京津城际高速铁路影响分析[J].岩土力学,2009,30(增刊2):269-272,276.

(责任编辑 闫杏丽)

Effect of different displacement boundary conditions and soil loss on underground pipeline

YU Jingliang1,SUN Lianwei2,CHAO Chunfeng3,4

(1.College of Harbor Engineering, Guangzhou Maritime Institute, Guangzhou 510725, China; 2.College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China; 3.Zhejiang Scientific Research Institute of Transport, Hangzhou 310006, China; 4.Sichuan Province University Key Laboratory of Bridge Non-destruction Detecting and Engineering Computing, Zigong 643000, China)

The previous research on the influence of shield tunnel excavation on underground pipeline is primarily based on the 3D model of tunnel excavation, and the strength reduction method is applied to the soil loss during the tunnel excavation or a certain soil loss rate is assumed. In fact, the soil loss during shield tunnel excavation is an important factor influencing the underground structures. In this paper, taking a practical project as an example, and based on the four radial displacement boundary conditions proposed by Park, the 2D model of the interaction between tunnel and pipeline is established to discuss the effect of tunnel excavation under different soil loss and boundary conditions on the pipeline. And the elliptical displacement boundary conditions and homogeneous displacement boundary conditions are compared. The results show that the elliptical displacement boundary conditions are more reasonable and the rate of soil loss should be controlled within 0.5% to ensure the safety of pipeline. And the appropriate grouting can reduce the settlement of pipeline.

shield tunnel; underground pipeline; two-dimensional model; finite element; numerical simulation

2015-04-16；

2015-08-15

四川省高校重点实验室开放基金资助项目(2014QZJ05)

余景良(1967-),男,江西九江人,广州航海学院副教授.

10.3969/j.issn.1003-5060.2016.10.019

U451

A

1003-5060(2016)10-1389-08