主轴回转误差引入飞切加工表面微波纹的形成机理与解决方案

孙郅佶 ， 毕 果 ， 安晨辉 ， 王振忠 ， 雷向阳 , 张清华

(1.厦门大学 物理与机电工程学院，福建 厦门 361005； 2. 成都精密光学工程研究中心，成都 610041)



主轴回转误差引入飞切加工表面微波纹的形成机理与解决方案

孙郅佶1，2， 毕 果1， 安晨辉2， 王振忠1， 雷向阳2, 张清华2

(1.厦门大学 物理与机电工程学院，福建 厦门 361005； 2. 成都精密光学工程研究中心，成都 610041)

为分析超精密飞切机床加工表面微波纹的形成机理，研究了主轴回转误差信息提取与表面形貌仿真技术，获取微波纹误差来源并研究解决方案。首先，在超精密飞切机床主轴上搭载五通道在线电容位移检测系统，并对采集到的信号进行误差分析提取。然后，建立飞切加工表面微观形貌三维仿真模型，仿真分析主轴误差引入的加工表面微波纹，并与表面检测结果比对确定误差来源。最后，通过调整主轴电机控制系统抑制该误差。三维仿真和实测结果相吻合，证实超精密飞切机床主轴转速波动导致的回转误差造成了工件表面1 Hz左右的规律性条纹，对主轴转速控制系统进行数字化改造后，基本消除了该因素导致的表面微波纹，表面粗糙度从5 nm以上抑制到2 nm左右,PV值优于10 nm。超精密飞切机床主轴转速波动会对飞切加工表面微观形貌以及表面粗糙度产生显著影响，需至少控制在0.5 r/min以内。

超精密飞切加工；主轴回转误差；粗糙度；微波纹

超精密切削设备是超精密加工领域非常重要的一个分支，以其高精度、高确定性和高效率等优势，被广泛应用于各种高精度模具及光学元器件的加工[1-2]，可以直接切削获得纳米级粗糙度的超光滑表面。近年来国内在超精密切削机床的设计和制造方面投入了巨大的精力，很大程度上突破了欧美对我国相关设备的垄断与技术封锁[3-7]。超精密飞切机床作为一种超精密加工技术，常用于加工工件的最终表面，尤其是一些易于潮解的光学晶体，无法采用传统的磨抛等光学加工方式时，单点金刚石飞切加工就成了唯一可以选择的加工手段，其加工后表面粗糙度可以达到5 nm以内，PV优于13 nm[2,4]。但是在实际的加工中，有许多的干扰因素会对机床的动态特性产生巨大的影响，进而影响加工工件的表面质量，其中主轴动态特性是一项很重要的干扰源[8-10]。CHENG等[12-13]将主轴与工件简化为一维刚度阻尼系统，并仿真了在特定频率的振动下工件表面粗糙度形貌。AN等[14]提出一种基于欧拉公式的表面粗糙度中频误差仿真模型。但是把主轴回转误差和加工表面形貌进行对应性研究的工作很少，对于由主轴回转误差引入的加工表面波纹缺乏明确的认知和有效的控制手段，因此需要结合主轴回转误差的动态测试开展加工表面的仿真建模，研究主轴动态特性对表面微观形貌的影响。

本文基于美国Lion Precision公司的SEA(Spindle Error Analyzer)双头标准球杆和5路高精度电容位移传感器测得的主轴回转误差数据，采用高速数据采集卡对原始数据进行采集，并对显著误差进行分离提取，然后输入到飞切加工表面三维形貌仿真模块，分析其对表面形貌的影响。实验研究表明该模型能准确有效的仿真出飞切加工表面出现的一种规律性微波纹，从而判断出这种微波纹的产生原因，并提出了解决方案。

1 理论模型

切削机床加工工件的本质是利用机床工具运动轨迹在工件表面精密复写来形成加工表面的。超精密飞切加工是一种确定性的加工方式，其加工工件的表面成形机理可以视作加工刀具截面轮廓沿刀具轨迹在加工工件表面的复印，而高速旋转的主轴，其回转误差对安装在飞刀盘外缘的刀具的位置精度有很大的影响。在仿真研究主轴回转误差对加工表面形貌影响时，需要将测得的主轴多通道位移数据转换为刀尖三维运动轨迹，并考虑到工件进给速度将刀尖运动轨迹从机床坐标系转换到工件坐标系内，形成刀尖在工件表面的运动轨迹，最终还需要考虑“刀具干涉”的影响[14]，如图1所示，对于L0位置，有三条刀纹对L0位置产生影响，但第三刀对最终加工工件的该位置高度起决定性作用。若主轴回转运动为理想运动，则加工工件表面将留下纳米级均匀等高轮廓，不会在工件表面产生明显的波纹度误差。

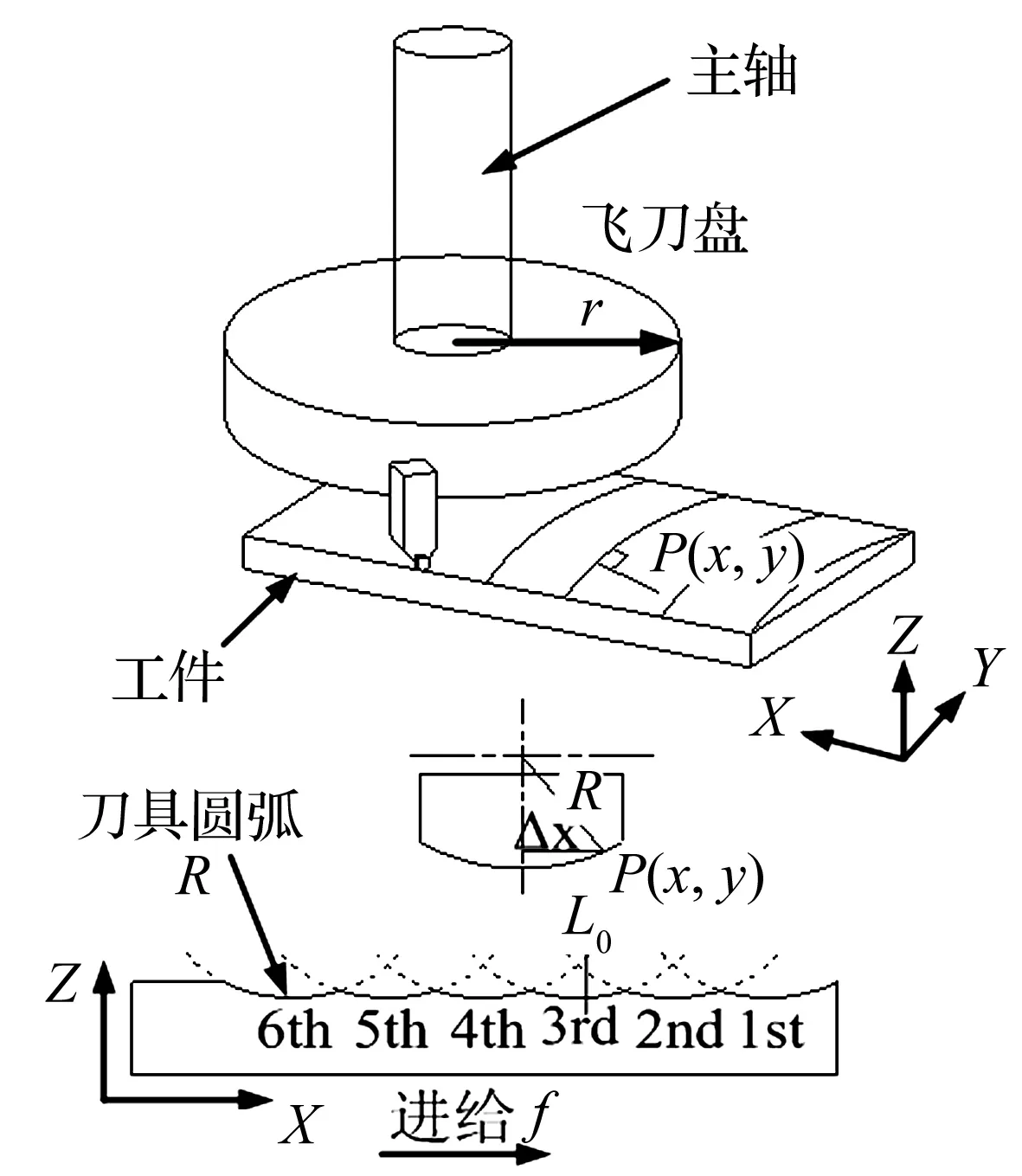
图1 工件表面成形机理Fig.1 Schematic surface topography of fly cut surface

1.1 表面形貌仿真模型

现阶段的超精密单点金刚石飞切加工中，作为最关键的部件的空气静压轴承的动态特性是学者们广泛研究的对象，LEE等[12-13]将主轴与工件系统简化为一维刚度阻尼系统，建立了较为完善的工件表面仿真模型，但并没有将其与主轴回转误差之间联系起来。AN等[2]对超精密飞切加工中频微波纹的产生进行了系统的分析，建立了飞切机床空气静压主轴的运动规律及其对加工工件表面中频微波的影响。

建立考虑到主轴回转误差的飞切加工表面三维形貌仿真模型，根据超精密飞切机床的加工原理，在如图1所示的XYZ直角坐标系中，首先计算出每到加工到工件任一点P(x,y)的加工时间：

T=Y×dt/(2×pi×r)

(1)

式中：Y为切削方向工件坐标，dt为主轴转动一周的时间，r为飞刀盘半径。

因此在时间T内切削方向上的切削距离x0可以表示为：

(2)

式中：f为加工进给速度。

工件表面任一点的高度可以由切削距离x0计算得出：

(3)

式中：R为刀尖圆弧半径。

根据上述分析，得到理想工件的加工的二维形貌仿真如图2所示，这个仿真结果体现了标准的刀具圆弧严格按照进给量在工件表面的复印，图中仿真的刀尖圆弧半径6 mm，进给率8.3 μm/r，其粗糙度值Rq=2 nm，PV=4.2 nm。

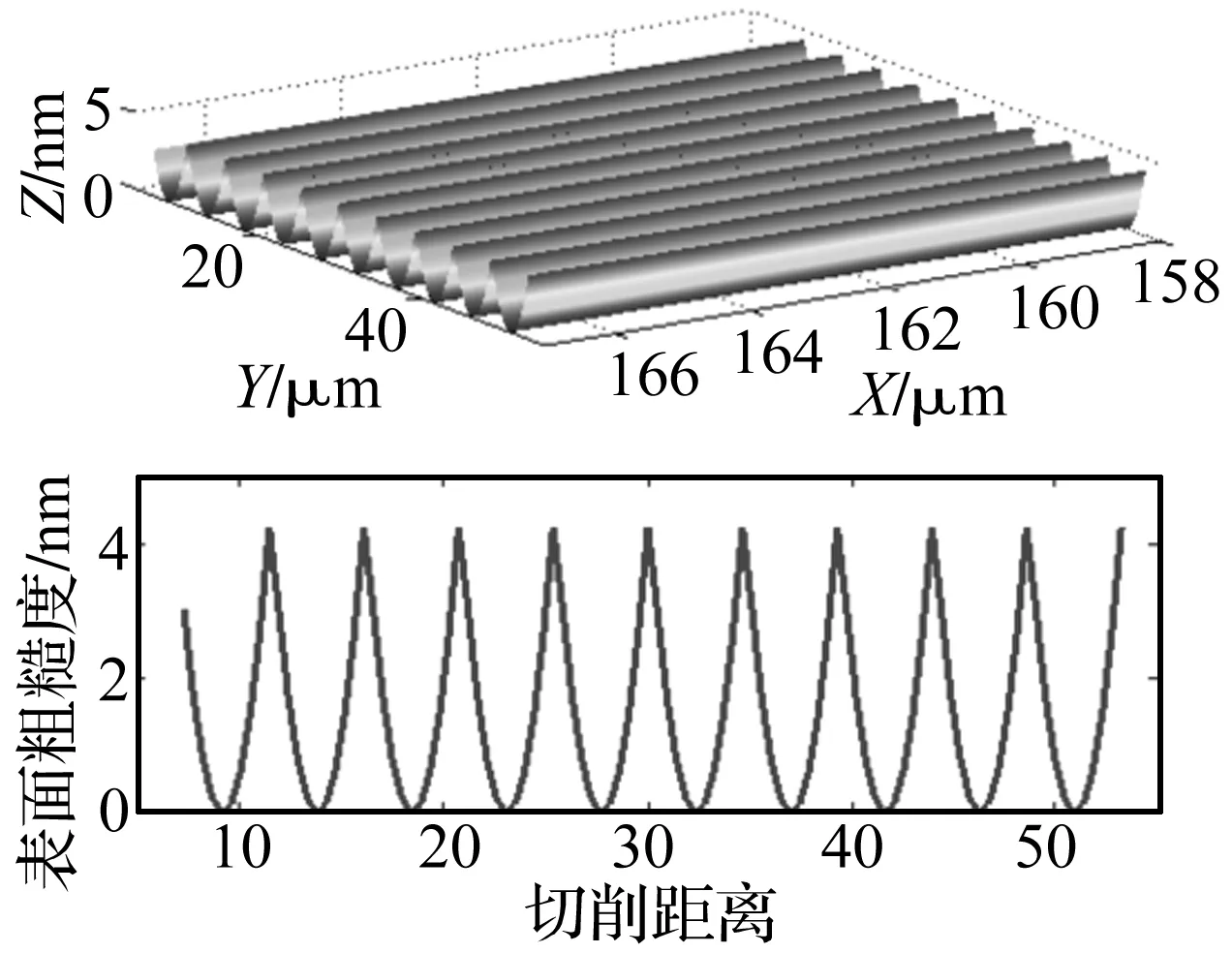
图2 理论表面微观形貌仿真Fig.2 Graphical illustration of ideal profile topography

而实际加工中主轴运动不会是理想的运动，因此会给加工工件的表面带来相应的误差。因此在式(3)的基础上引入主轴回转误差，得到加工工件表面成形计算公式：

(4)

式中:M为主轴回转误差。

对于超精密飞切加工而言，切削深度和和进给率都很小，在考虑到振动情况时，加工工件的表面形貌就会受到刀具干涉的影响，如图1所示，因此计算相邻几条刀纹对工件同一点的干涉作用，取干涉后残留的最低点，即为加工最终表面的残余高度。

1.2 主轴回转误差测试方案

建立主轴回转误差在线测试系统硬件结构，如图3所示。测试系统硬件由美国Lion Precision公司的精英系列CPL-290 测试设备和MFG3-1905双标准球构成，主轴回转误差数据使用IO-tech Zonic Book 618E数据采集器采集。测试对象为一台国内自研的立式超精密飞切加工机床，大圆弧刃天然金刚石刀具固定在大飞到盘的外缘做高速旋转，工件则固定在工作台上做水平方向进给，从而完成平面光学元件的加工任务，加工后的表面使用具有3 nm分辨率和500 mm行程的WykoRST-plus (Veeco Metrology Group)粗糙度测量仪对粗糙度进行检测。

该超精密机床主轴采用气浮轴承支撑，由直连在主轴上的电机轴提供驱动，若在一定转速范围内认为主轴旋转部分为刚体，则通过测量主轴顶部轴端的五个方向的位移规律，可以换算出固定于主轴下端刀尖部位的运动特征。在不同转速下，主轴回转误差有一定的变化，本文对50 r/min到800 r/min每隔10 r/min测一组数据，并对每组数据进行频域分析。

图3 主轴回转误差在线测试系统硬件构成Fig.3 Hardware of online spindle error test system

根据实验测试方案对主轴回转误差进行测量。不同转速下最佳正弦拟合去除一阶信号的转频的频谱均具有类似图4的分频现象，即在主轴转频附近出现两个关于主轴转频对称的频率分量，从图中可以看出其转速的频带较宽，通过最佳正弦拟合去除一阶信号的办法无法去除图5(a)为不同转速下分频频率与转频的关系。

图4 超精密切削机床主轴回转误差X方向频谱Fig.4 The spectral of the spindle error motion

图5 条纹周期Fig.5 Graphical illustration of the relationship between the fringe period and spindle speed

根据图5(a)所示的关系，拟合出分频频率与转频的关系式为：

F1=1.023×F0-1.026

(5)

式中:F1为分频频率，F0为转频。

由于分频和转频之间并不是严格的倍频关系，并且由于飞刀切削是不连续切削，如图1(a)所示，主轴转动一圈在工件表面形成一道切削条纹，但是每刀切削时间内，分频并不会回到前一刀切削的相位，而造成沿进给方向每一刀切削，分频将会在不同的相位点上对该点形成作用，因此由于分频引起的条纹周期t，即经过时间t后分频频率的相位回到初始初始相位的计算如下：

t×n×Δ=2π

(6)

式中:n为时间t内主轴转动圈数，Δ为转频F0和分频F1之间每转一圈的相位差。

因此，整理上式得：

(7)

因此由于分频造成的加工工件表面周期与转速关系如图5(b)所示。

根据图5(b)可以得出结论，不同转速下刀尖每次切刚到工件时的相位差差异很小，尤其在实际加工中，主轴转速一般不超过500 r/min，因此该分频现象在工件表面引起的条纹周期在一定范围内基本不随转速而变化，其时间周期约为1秒。

2 仿真及实验

2.1 仿真和实验对比

对主轴分频现象引入的加工表面形貌误差进行仿真，并对实际切削加工表面进行检测比对，在相同的切深4 μm的情况下，对实际加工工艺参数下的加工表面进行仿真和实验验证，仿真结果和实测结果如表1所示所示，其粗糙度等指标如表2所示。

表1 仿真结果和实验结果对比

表2 粗糙度仿真和实测结果

从表1的图中可以清楚的看到工件表面出现了周期性条纹，并且仿真结果和实验结果在条纹的间距上高度吻合，小于3%，峰谷值的变化趋势也是一致的。

从表2工件表面粗糙度上出现的条纹的周期接近于每秒的进给距离，因此验证了式(7)的正确性。同时从表2中还可以看出，由于该分频现象造成的表面粗糙度大于实测表面粗糙度的2 nm，PV值大于7 nm，考虑到加工工件的表面粗糙度不大于10 nm，PV值不大于45 nm，因此该分频现象对加工工件的表面粗糙度造成了很大的影响。

上述分析验证了加工工件表面1 Hz条纹产生的原因，对机床的优化改进有重要意义。

2.2 机床改进后加工结果

根据主轴回转误差测试数据的分析，可知造成该分频现象的主要原因是主轴电机的转速波动，将主轴电机的转速信号由模拟控制改为数字控制后，转速波动得到大幅抑制。改进后主轴回转误差测试结果得到很好的改善，进行正弦拟合并去除转频后，该频率处的曲线很平坦，分频现象也消失，证明了转速在频率域上的带宽已经大幅缩窄。测试结果如图6(正弦拟合去除一阶频率信号)。

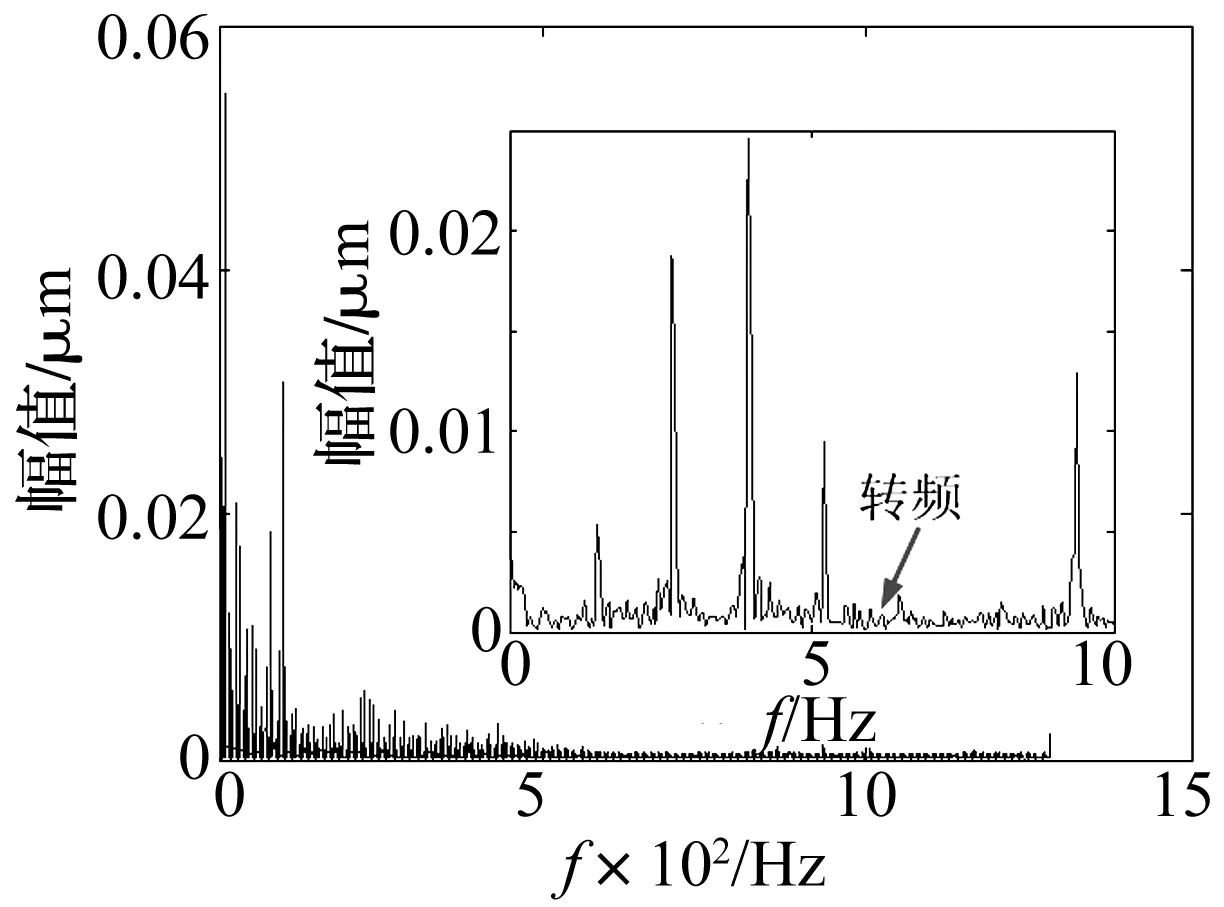
图6 电机控制方式更改后超精密切削机床主轴X方向频谱Fig.6 The spectral of the spindle error motion after spindle mechanical properties improved

对数字控制方式下以相同的加工工艺参数加工工件表面粗糙度的测试结果显示，没有分频现象的干扰，加工转速390 r/min，进给速度60 μm/s下，多次切削工件表面，并对加工工件表面进行测量，其表面粗糙度优于3 nm，峰谷值优于9 nm。粗糙度检测结果如图7所示，多次切削下加工工件表面粗糙度及PV值如图8所示。

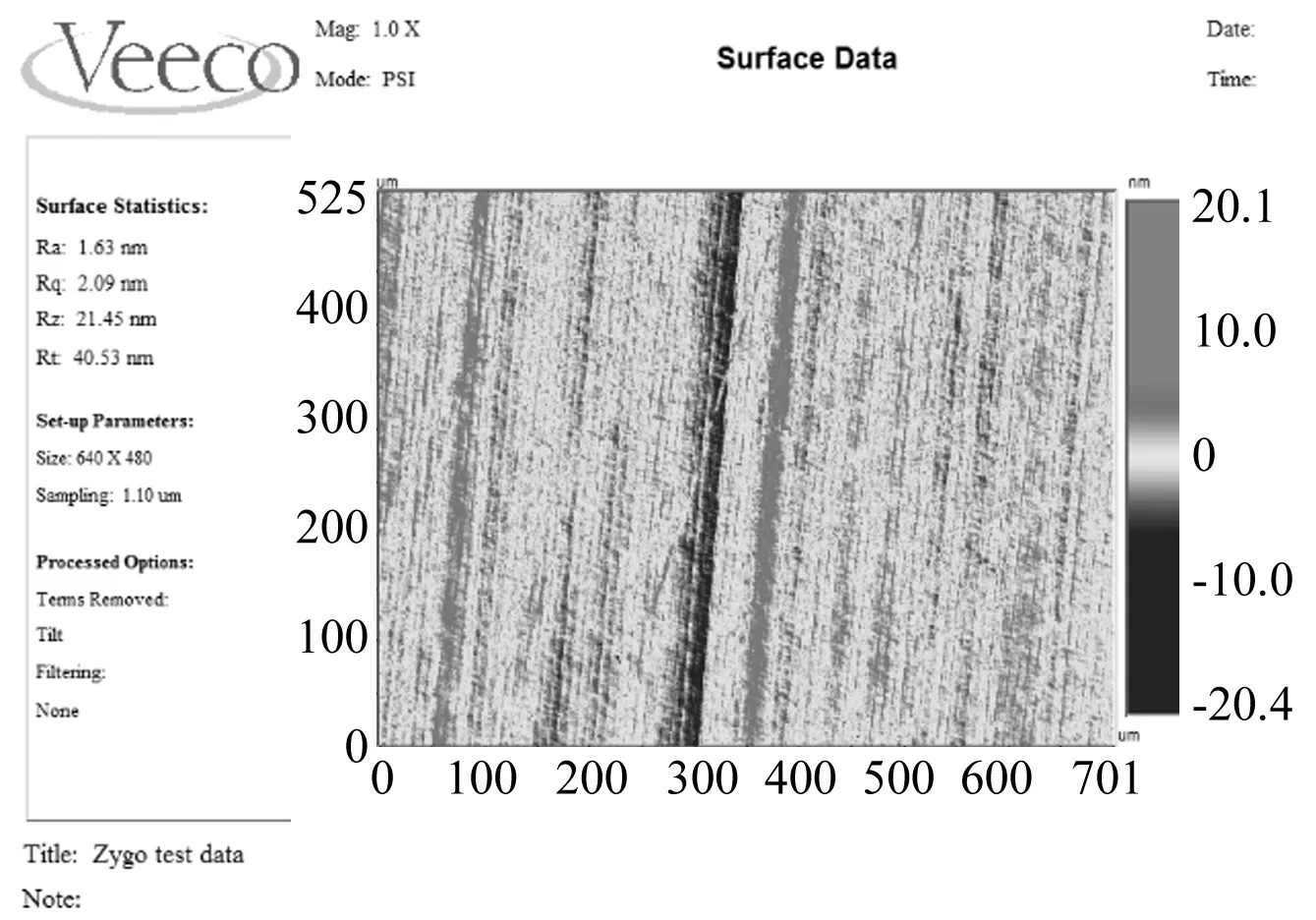
图7 数字控制电机转速后加工表面粗糙度实测Fig.7 Measured surface profiles after spindle mechanical properties improved

图8 多次加工表面粗糙度实测Fig.8 Measured surface roughness after spindle mechanical properties improved

根据图6～8可见，对电机进行控制方式更改后，机床性能得到很大的改善，与转频呈一定函数关系的分频现象被抑制后，加工工件的表面结果得到很大的改善，表面粗糙度Rq值从5 nm以上抑制到2 nm左右。

3 结 论

本文根据超精密切削机床加工工件表面粗糙度控制的迫切需求，对基于标准球的五通道电容位移传感器测得的主轴回转误差数据进行分析发现在转频左右对称位置各出现一个分频。从理论上分析了超精密飞切加工机床表面粗糙度成形机理，并建立超精密飞切机床加工工件表面粗糙度成形的仿真模型，并对主轴回转误差中特有的分频现象对工件表面粗糙度的影响进行仿真及实验研究。通过仿真结果可以看出，该分频现象会导致加工工件表面出现约1 Hz的条纹，并且该分频造成的表面粗糙度均大于2 nm。实际加工后工件表面的实测结果与仿真结果一致，证明主轴回转误差分频现象是导致工件表面产生1 Hz条纹的主要因素，同时验证了表面粗糙度模型的正确性。经机床主轴电机转速控制方案改进，分频消失并获得无显著条纹的加工表面，其表面粗糙度优于3 nm，PV值优于10 nm。

[1] 袁巨龙,张飞虎,戴一帆,等. 超精密加工领域科学技术发展研究[J]. 机械工程学报, 2010，46(15): 161-177.

YUAN Julong, ZHANG Feihu, DAI Yifan, et al. Development research of science and technologies in ultra-precision machine field [J].Journal of Mechanical Engineering, 2010，46(15): 161-177.

[2] 安晨辉,王健,张飞虎,等. 超精密飞刀切削加工表面中频微波产生机理[J]. 纳米技术与精密工程,2010,8(5):439-446.

AN Chenhui, WANG Jian, ZHANG Feihu, et al. Mid-spatial frequency micro-waviness on machined surfaces by ultra-precision fly-cutting [J]. Nanotechnology and Precision Engineering, 2010, 8(5):493-446.

[3] 杨毅青，刘强，申江丽，等. 基于动力学及切削特性耦合的数控机床结构设计[J]. 振动与冲击,2013, 32(10): 198-202.

YANG Yiqing, LIU Qiang, SHEN Jiangli, et al. Machine tool structure design based on the coupling analysis of dynamics and cutting performances [J]. Journal of Vibration and Shock, 2013, 32(10): 198-202.

[4] 张文生, 张飞虎, 董申. 光学脆性材料的金刚石切削加工[J]. 光学精密工程, 2003, 11(2): 139-143.

ZHANG Wensheng, ZHANG Feihu, DONG Shen. Diamond cutting of optical brittle materials [J]. Optics and Precision Engineering, 2003, 11(2): 139-143.

[5] 于英华, 徐兴强, 徐平. 切削颤振的在线监测与控制研究现状分析[J]. 振动与冲击, 2007, 26(1): 130-166.

YU Yinghua, XU Xingqiang, XU Ping. A review of on-line monitoring and control for machine tool chatter [J]. Journal of Vibration and Shock, 2007, 26(1): 130-166.

[6] 许乔, 王健, 马平,等. 先进光学制造技术进展[J]. 强激光与粒子束, 2013, 25(12): 3098-3015.

XU Qiao, WANG Jian, MA Ping, et al. Progress of advanced optical manufacturing technology [J]. High Power Laser and Particle beam,2013, 25(12): 3098-3015.

[7] 夏欢, 陶继忠. 空气静压球面轴承主轴回转精度测试研究[J]. 轴承, 2013(7): 56-58.

XIA Huan, TAO Jizhong. Test on rotation precision of aerostatic spherical bearing’s spindle [J]. Bearing,2013(7): 56-58.

[8] NOGUCHI S, MIYAGUCHI K. An evaluation method of radial accuracy for hydrostatic air spindles considering radial movement of the rotating center[J]. Precision Engineering, 2003,27:395-400.

[9] CAO Yuzhong, ALTINTAS Y. Modeling of spindle-bearing and machine tool systems for virtual simulation of milling operations[J]. International Journal of Machine Tools & Manufacture, 2007,47:1342-1350.

[10] 熊万里,侯志泉,吕浪.液体静压主轴回转误差的形成机理研究[J].机械工程学报, 2014,50(7):112-118.

XIONG Wanli, HOU Zhiquan, LÜ Lang. Study on the mechanism of hydrostatic spindle rotational error motion[J]. Journal of Mechanical Engineering, 2014, 50(7): 112-118.

[11] CHENG M N, CHEUNG C F, LEE W B, et al. Kinematics and experimental analysis of form error compensation in ultra-precision machining[J]. International Journal of Machine Tools & Manufacture, 2008,48:1090-1102.

[12] LEE W B, CHEUNG C F. A dynamic surface profile model for the prediction of nano surface generation in ultra-precision machining[J]. International Journal of Mechanical Sciences, 2001,43:961-991.

[13] CHEUNG C F, LEE W B. Characterisation of nanosurface generation in single-point diamond turning[J]. International Journal of Machine Tools and Manufacture,2001,41:851-875.

[14] AN C H, ZHANG Y, XU Q, et al. Modeling of dynamic characteristic of the aerostatic bearing spindle in an ultra-precision fly cutting machine[J]. International Journal of Machine Tools & Manufacture, 2010,50:374-385.

Formation and solving for the micro-waves of fly-cut surface introduced by spindle error

SUN Zhiji1,2, BI Guo1, AN Chenhui2, WANG Zhenzhong1, LEI Xiangyang2, ZHANG Qinghua2

(1. Department of Mechanical and Electrical Engineering, Xiamen University, Xiamen 361005, China；2. Chengdu Fine Optic Engineering Research Center, Chengdu 620041, China)

In order to find out the formation mechanism of micro-waves on the fly-cut surface, the spindle motion error was sampled and a 3D topography simulation model was compiled. Firstly, a nano-class testing and evaluation system was established on the fly cutting machine, the displacement data was sampled and the spindle motion error was analyzed. Then a 3D surface profile topography simulation model was established to analyze the micro-waves caused by the spindle motion error. The simulated surface was compared with the measured surface to find out the error sources. Finally, the characteristics of spindle were improved by adjusting the control system of the spindle motor. The simulated 3D surface profile topography was similar to that of the measured profile, which verified that the macro-waves was caused by the undulate of the spindle speed. When the spindle characteristics was improved, the macro-waves caused by the spindle motion error almost disappeared, and the surface roughness reduced from more than 5 nm to 2 nm. It is thus concluded that the undulate of ultra-precision fly cutting machine spindle speed causes macro-waves on the work-piece surface, and the undulate spindle speed must less than 0.5 r/min.

ultra-precision fly cutting; spindle motion error; surface roughness; macro-waves

高档数控机床与基础制造装备《强激光光学元件超精密制造关键装备研制》(2013ZX04006011-102-001)

2015-05-05 修改稿收到日期：2015-09-17

孙郅佶 男，硕士，1990年10月生

安晨辉 男，博士，副研究员，1981年4月生

TH133.36

A

10.13465/j.cnki.jvs.2016.20.032