基于GAMP和EEMD的滚动轴承故障诊断研究

潘宏侠， 张 翔

(中北大学 系统辨识与诊断技术研究所,太原 030051)



基于GAMP和EEMD的滚动轴承故障诊断研究

潘宏侠， 张 翔

(中北大学 系统辨识与诊断技术研究所,太原 030051)

针对实验中采集到的滚动轴承的振动信号具有成分复杂和较强的非平稳性等特点，提出采用基于遗传算法优化的匹配追踪算法(GAMP)和总体平均经验模式分解(EEMD)相结合的方法，实现对滚动轴承振动信号的处理与分析。首先，利用GAMP算法将滚动轴承振动信号线性展开成能够较好的匹配该信号特征结构的一系列高斯函数，达到消除干扰噪声锁定信号的局部特征的目的；然后，针对GAMP消噪后的振动信号中可能存在的虚假频率成分或不连续的分量，利用EEMD方法来予以剔除，通过傅里叶变换将处理后的振动信号从时域转化到频域，提取出故障振动信号的故障频率；最后，采用支持向量机(SVM)对滚动轴承的正常和故障振动信号进行分类，实现了对滚动轴承的故障诊断。

GAMP；EEMD；SVM；滚动轴承；故障诊断

滚动轴承是支承传动轴的重要部件，由于它具有摩擦因数小、结构紧凑、运转精度高以及维护和更换方便等优点，因而被广泛的应用于各类机械设备中。但是，滚动轴承在高速、高精度或重载下随传动轴连续不断的旋转时，极易发生故障，将直接影响机械设备的工作性能。因此，对滚动轴承故障诊断的研究将能及时有效的发现故障并保证机械设备的正常运行。

故障特征信息提取是滚动轴承故障诊断中最为关键的问题之一[1]，由于获取滚动轴承振动信号的系统具有拆装简便、操作容易和性能可靠等一系列优点，因此，现阶段对滚动轴承的故障诊断主要是分析和处理它的振动信号。在对滚动轴承故障进行诊断时，从现场采集到的振动信号不仅成分复杂而且受到背景噪声的干扰，使得故障特征信息被掩盖，造成诊断结果的不准确。由于GAMP算法是以具有简谐振动和双面指数衰减振动的高斯函数对振动信号进行线性展开，能很好的匹配振动信号的结构特征，达到消除噪声信号从而锁定信号的局部特征的目的[2]，针对GAMP算法消噪后的信号可能存在的虚假和不连续成分，采用EEMD方法能够有效的将其予以剔除，从而比较准确的提取出振动信号的特征频率。因此，本文提出将GAMP和EEMD相结合的方法应用于轴承故障诊断的研究中。

1 GAMP算法原理

匹配追踪(MP)算法[3]是将信号的时域序列展开为一系列参数化波形函数加权和的一种迭代分解算法：

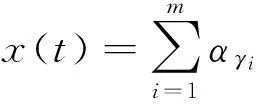
(1)

式中：φγi为波形函数，ri=ri-1-αγiφγi为残余信号，分解次数i=1时有r0=x(t)，αγi为加权系数，它是残余信号ri-1与波形函数φγi之间的正则内积，即：

αγi=〈ri-1,φγi〉

(2)

MP算法的每一次分解都是使式(1)中得到的残余信号ri(i=1,2,…,m)的范数取值最小，即：

min‖ri‖2=min‖ri-1-αγiφγi‖2

(3)

该式等价于：

(4)

该问题属于多维优化的范畴，可以通过Newton-Raphson算法[4]和遗传算法[5]等优化方法来进行计算求解。由于遗传算法(Genetic Algorithms,GA)具有很强的适应性和同时在空间中搜索多个点的功能，它使用不受确定性规则控制的随机算子面向全局最优解的方向进行搜索，极大的提高了计算效率，在组合和函数优化、信号处理和模式识别等领域的应用取得了不错的成效。因此，本文将采用基于遗传算法优化的匹配追踪算法(GAMP)算法来分解信号达到消噪的目的。

采用GAMP算法分解信号x(t)的过程如图1所示。

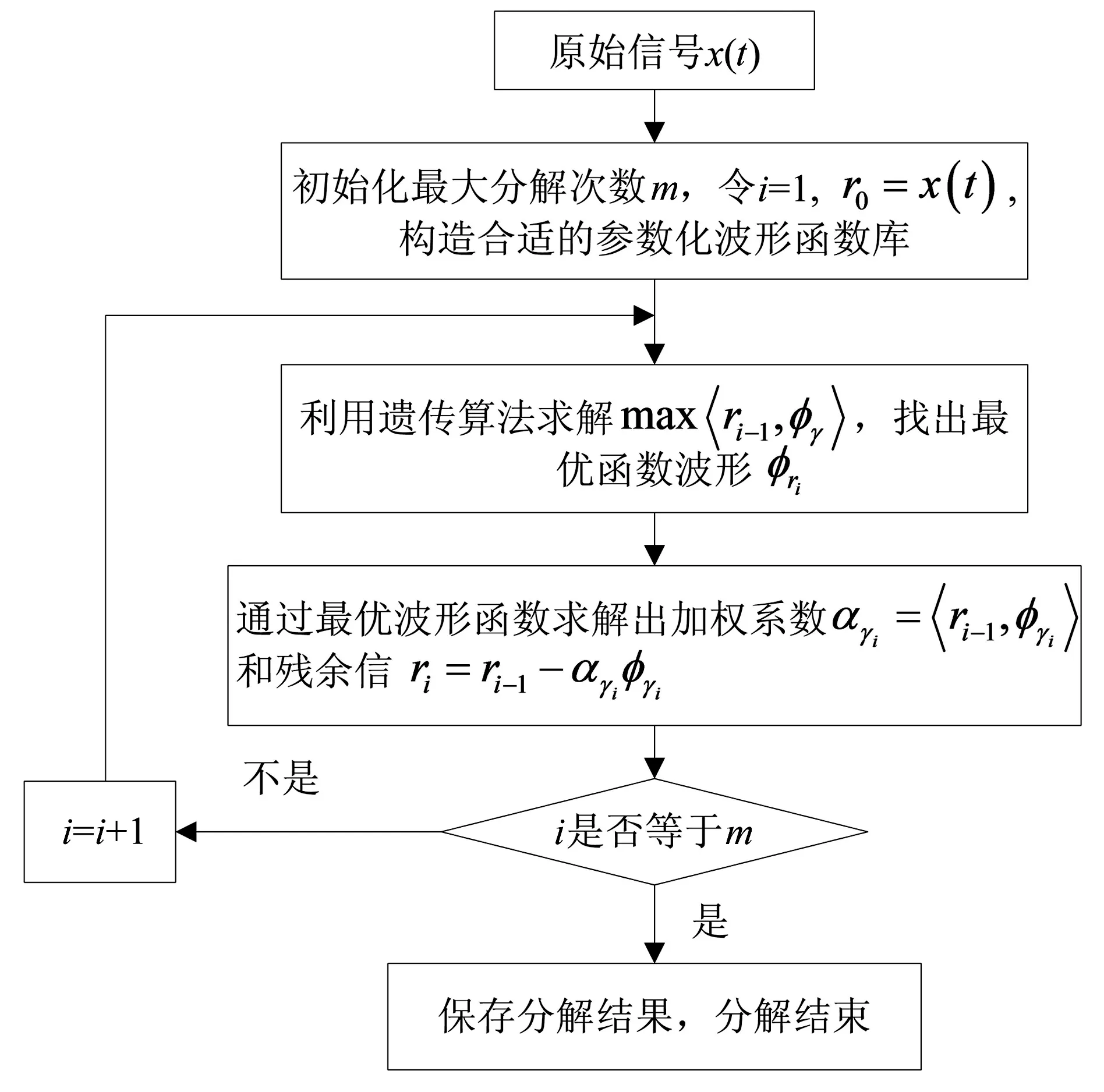
图1 GAMP算法分解过程的流程图Fig.1 GAMP algorithm decomposition process flow chart

采用GAMP算法分别对在正弦信号x(t)=sin(0.03t)中加入噪声信号构成的仿真信号分解5次、10次、13次、15次和20次降噪结果如图2所示。

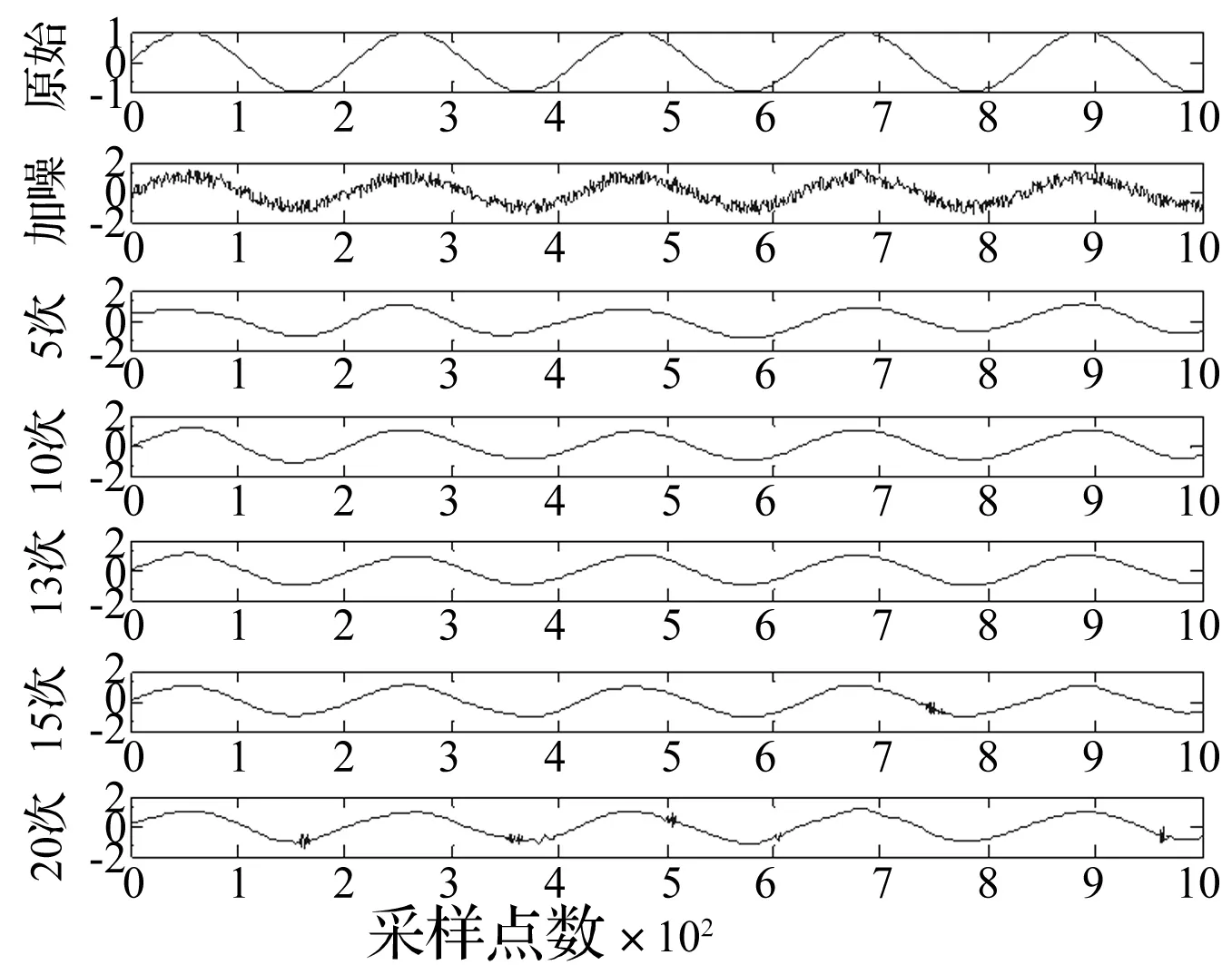
图2 GAMP算法不同次数分解的消噪结果Fig.2 De-noising results of different time decomposition using GAMP algorithm

为了说明GAMP算法具有可靠的消噪功能，这里用信噪比来衡量消噪效果，表达式为：

(5)

式中：x为初始信号，z为消噪后的信号。

将图2中各分解结果的SNR和分解时间记录在表1中。

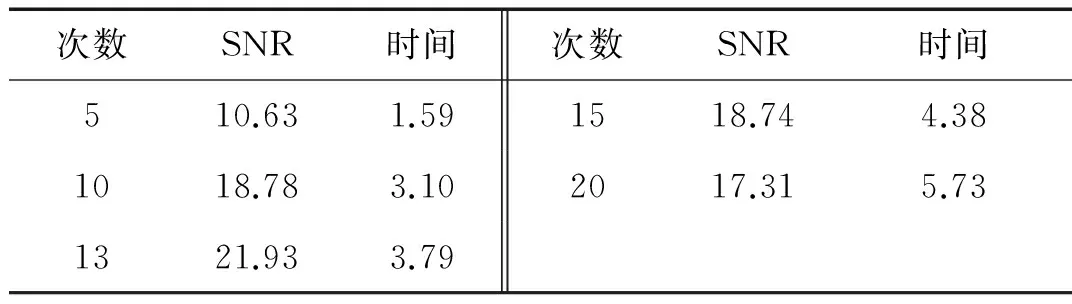
表1 各分解结果的SNR和分解时间

从图2和表1能清楚的看出，GAMP算法可以对原始信号进行有效的消噪，选择合适的分解次数能达到非常好的消噪效果。

2 EEMD分解原理

经验模式分解(Empirical Mode Decomposition，EMD)能把非线性、非平稳信号分解为一系列的本征模函数(Intrinsic Mode Function，IMF)，在机械故障诊断中处理和分析信号方面得到了广泛的应用。但是当信号中存在时间尺度跳跃变化、脉冲干扰时，EMD分解信号得到的IMF将会出现模态混叠的现象[6]。总体平均经验模式分解(Ensemble Empirical Mode Decomposition，EEMD)是在EMD的基础上发展而来的，它是通过在不连续信号中加入高斯白噪声，使其成为连续信号[7-8]，然后经过EMD分解，得到不存在模态混叠的IMF分量[9]。EEMD分解信号x(t)的过程如图3所示。

图3 EEMD分解过程的流程图Fig.3 EEMD decomposition process flow chart

为了说明EEMD能够消除模态混叠，仿真一个由正弦波x(t)=sin(πt)和小幅冲击成分叠加而成的信号，其中正弦波的采样频率为200 Hz，采样点数为1 200，小幅冲击成分为0.2倍的不连续随机信号组成。分别采用EMD和EEMD方法分解仿真信号得到的结果如图4和图5。

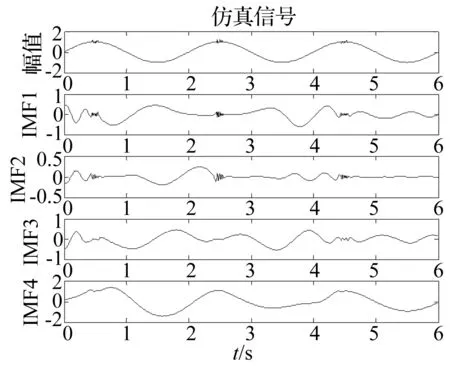
图4 EMD分解仿真信号Fig.4 Simulation signal of EMD decomposition

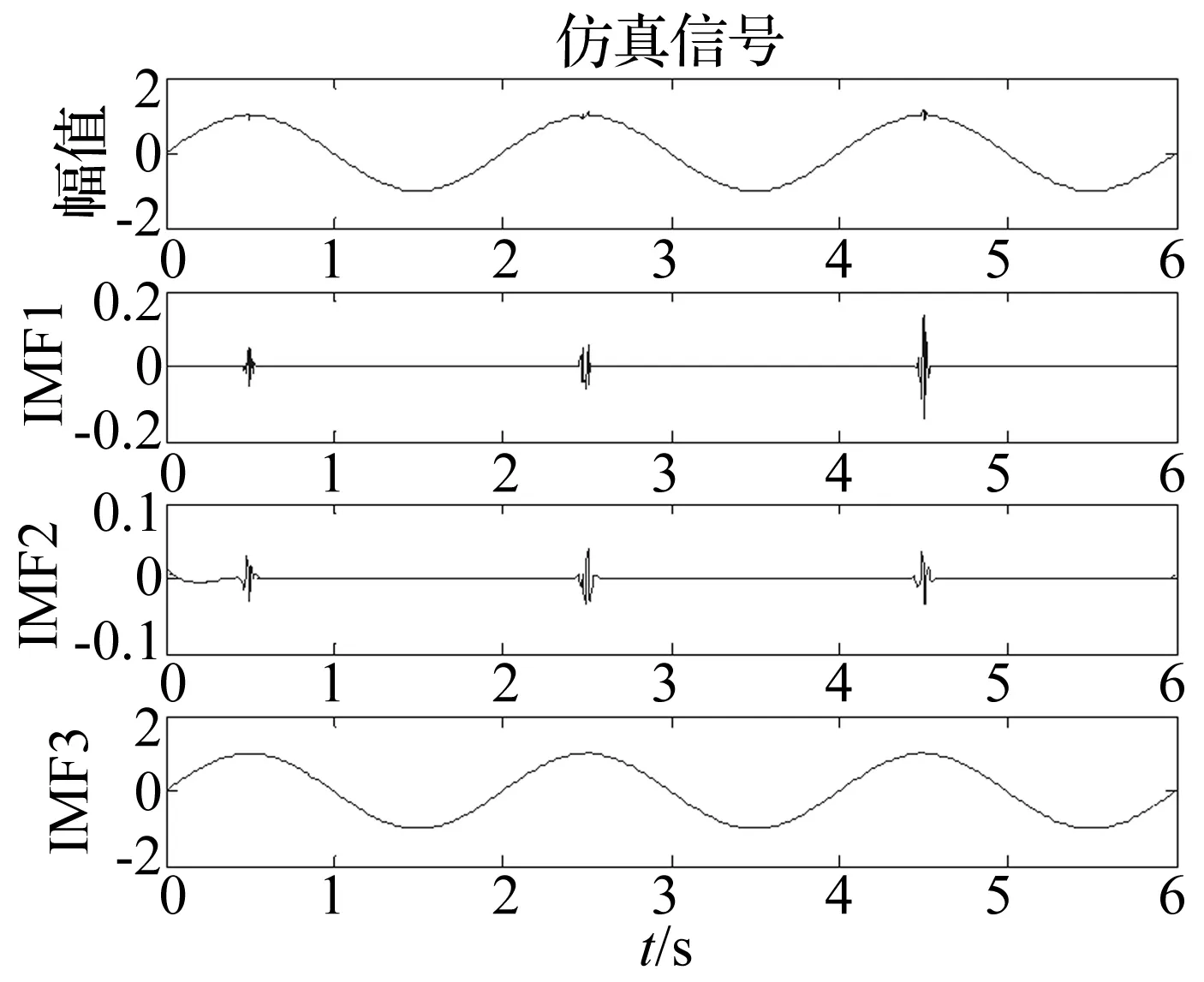
图5 EEMD分解仿真信号Fig.5 Simulation signal of EEMD decomposition

从图4和图5可以清楚的看到，仿真信号经过EMD分解之后得到的IMF分量出现了非常明显的畸变：正弦波和小幅冲击成分被分解到了同一个IMF中；仿真信号经过EEMD分解之后得到的IMF分量没有出现畸变，正弦波和小幅冲击成分被比较准确的分解出来。

3 GAMP算法和EEMD结合

GAMP算法是以具有简谐振动和双面指数衰减振动的高斯函数对振动信号进行线性展开，能很好的匹配振动信号的结构特征，达到消除噪声信号从而锁定信号的局部特征的目的，但是，当采用GAMP算法分解信号进行消噪时，由于选取的分解次数可能不是很合适，消噪后的信号中可能会存在虚假成分或不连续的分量。从图2和表1可以看出，若选取的分解次数较小时，由于GAMP算法分解的不完全，消噪得到的信号也是不完整的；若选取的分解次数较大时，由于GAMP算法分解的过多，消噪得到的信号中混入的噪声信号也越来越多。在实际中，采集到的齿轮箱振动信号成分非常复杂，采用GAMP消噪时，我们不能确定准确的分解次数，为了消噪后的信号保持原有信号的特点，分解次数一般会比较高，那么随之而来的是混入的噪声信号也会增加，为此，利用EEMD方法分解GAMP算法消噪的信号，能达到剔除虚假成分且不出现模态混叠的目的。

采用GAMP算法对在正弦信号x(t)=sin(0.03t)中加入噪声信号构成的仿真信号分解20次降噪结果如图6所示。

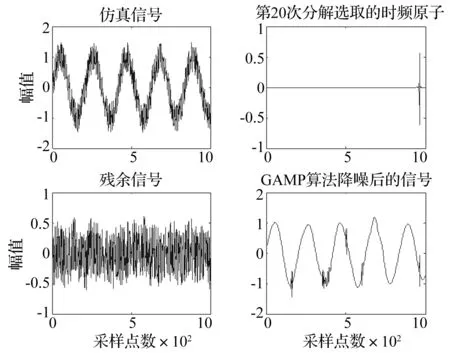
图6 GAMP算法20次分解仿真信号Fig.6 Simulation signal of 20 times decomposition using GAMP algorithm

从图6可知，消噪后的信号混入了一些离散的干扰信号，这些干扰信号将会给后续的信号分析带来影响，使得信号分析的结果出现偏差。分别采用EMD和EEMD分解图6中的消噪后的信号如图7和8所示。

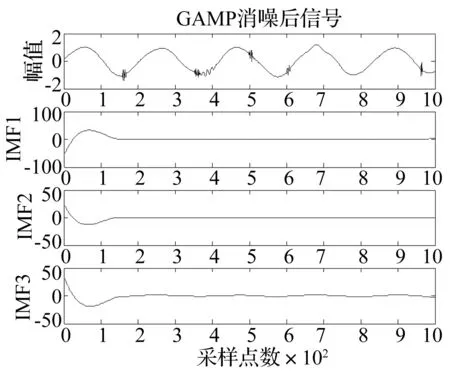
图7 EMD分解消噪信号的结果Fig.7 Result of EMD decomposing the denoise signal

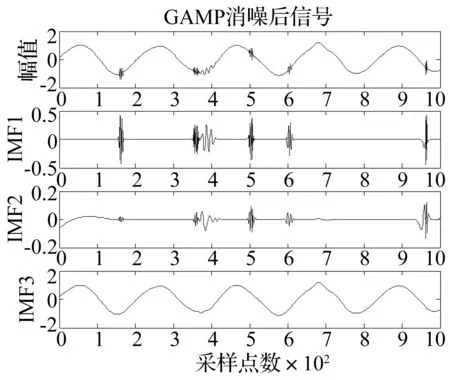
图8 EEMD分解消噪信号的结果Fig.8 Result of EEMD decomposing the denoise signal

图7中，经过EMD分解得到的IMF分量的幅值较GAMP消噪后的信号幅值发生了很大的变化，而且波形出现了畸变；图8中，分解得到IMF1和IMF2基本就是消噪带来的干扰信号，IMF3与原始信号基本上相似。因此，采用GAMP算法和EEMD相结合的方法能够很好的实现对信号的处理与分析。

针对实验中采集到的滚动轴承的振动信号具有成分复杂和较强的非平稳性等特点，采用GAMP算法和EEMD相结合的方法能很好的匹配振动信号的结构特征，达到消除噪声信号从而锁定信号的局部特征的目的，并且在能很好的剔除出消噪后信号中的虚假成分且不出现模态混叠的现象,因此，本文将该方法运用于轴承故障诊断实验中。

4 实 验

本实验的对象是齿轮箱传动系统，它是由一个MD280T90G/110P变频器、一个Y280M-4型三相异步电动机、两个CGQ-100转矩转速传感器、两个ZS65型减速箱(一个用作减速，另一个用作增速)和一个WZ-650型涡流制动器通过联轴器连接组成见图9。

图9 实验平台Fig.9 Experiment platform

为了说明齿轮箱的故障设置点以及传感器安放位置，画实验平台结构简图如图10所示。

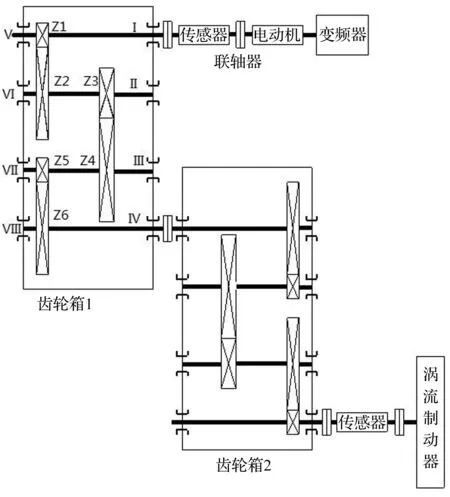
图10 实验平台结构简图Fig.10 The structure diagram of experiment platform

图10中，齿轮箱1中的四对轴承的上方表面箱体安装了标号为Ⅰ到Ⅷ的8个压电式加速度传感器，通过电荷放大器将传感器获取的微弱电信号进行放大，然后利用DASP数据采集仪器将放大后的电信号处理成数据储存到计算机中用于后期的数学分析与处理。

实验中获取的数据是在齿轮箱输入轴转速为1 200 r/min，涡流制动器励磁电流为1 A，采样频率为4 000 Hz，采样点数为4 000下的第Ⅵ测点的振动信号,根据ZS65型减速箱中齿轮及传动轴的参数，得到齿轮及传动轴的基频与倍频如表2所示。在齿轮箱中，滚动轴承的外圈与轴承座间的配合比较松，当其出现故障时，会激起外圈的固有频率，即齿轮和轴承上的零部件振动激励外圈共振的频率与自由状态下的固有频率是基本相同的，滚动轴承故障分析是在轴承发生局部故障时分析故障特征频率。实验中，将第Ⅵ测点下的30309型滚动轴承的外圈内侧划一道刮痕设置为轴承故障如图11所示，根据其基本参数计算出它的外圈故障频率为32.86 Hz，外圈故障频率为外圈出现故障时，造成外圈、保持架以及滚动体的接触不良，在随旋转轴旋转的过程中激励外圈振动的频率。

采用GAMP方法对轴承外圈故障振动信号分解2 500次而实现消噪的重构信号如图12所示。对轴承外圈故障信号经过GAMP消噪得到的信号进行EEMD分解，得到如图13的一系列IMF分量。IMF是对原始信号的近似正交的表达，真正的IMF和原始信号之间应该有很好的相关性，EEMD分解得到的IMF与消噪后信号的相关系数如表3所示，前5个IMF分量与消噪后信号的相关度比较好应保留，后面6个IMF分量的相关度较差应予以剔除，剔除虚假IMF之后得到的重构信号与残差如图14所示。经GAMP消噪和EEMD分解重构的信号通过FFT变换得到的频谱如图15所示。

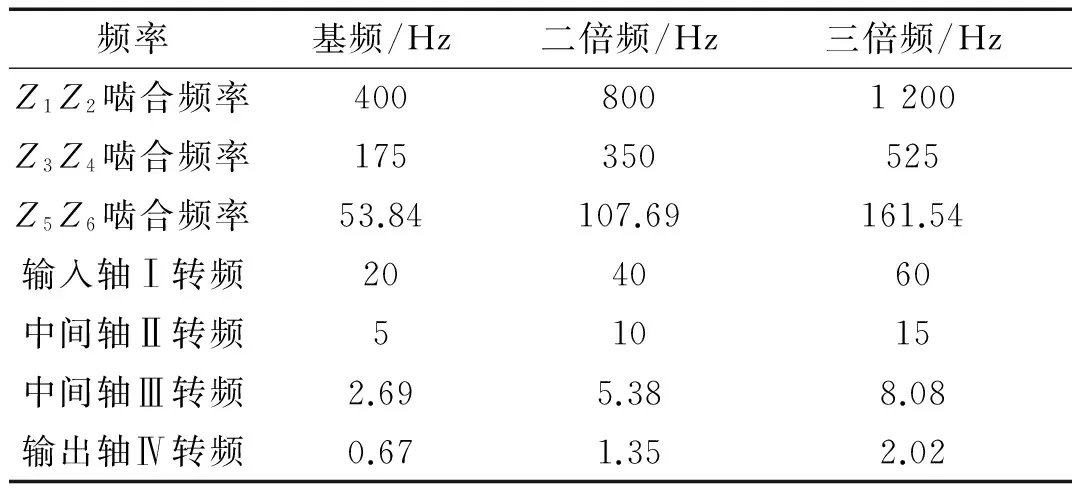
表2 ZS65型减速箱中齿轮和传动轴基频与倍频

图11 轴承外圈故障Fig.11 Bearing outer ring fault

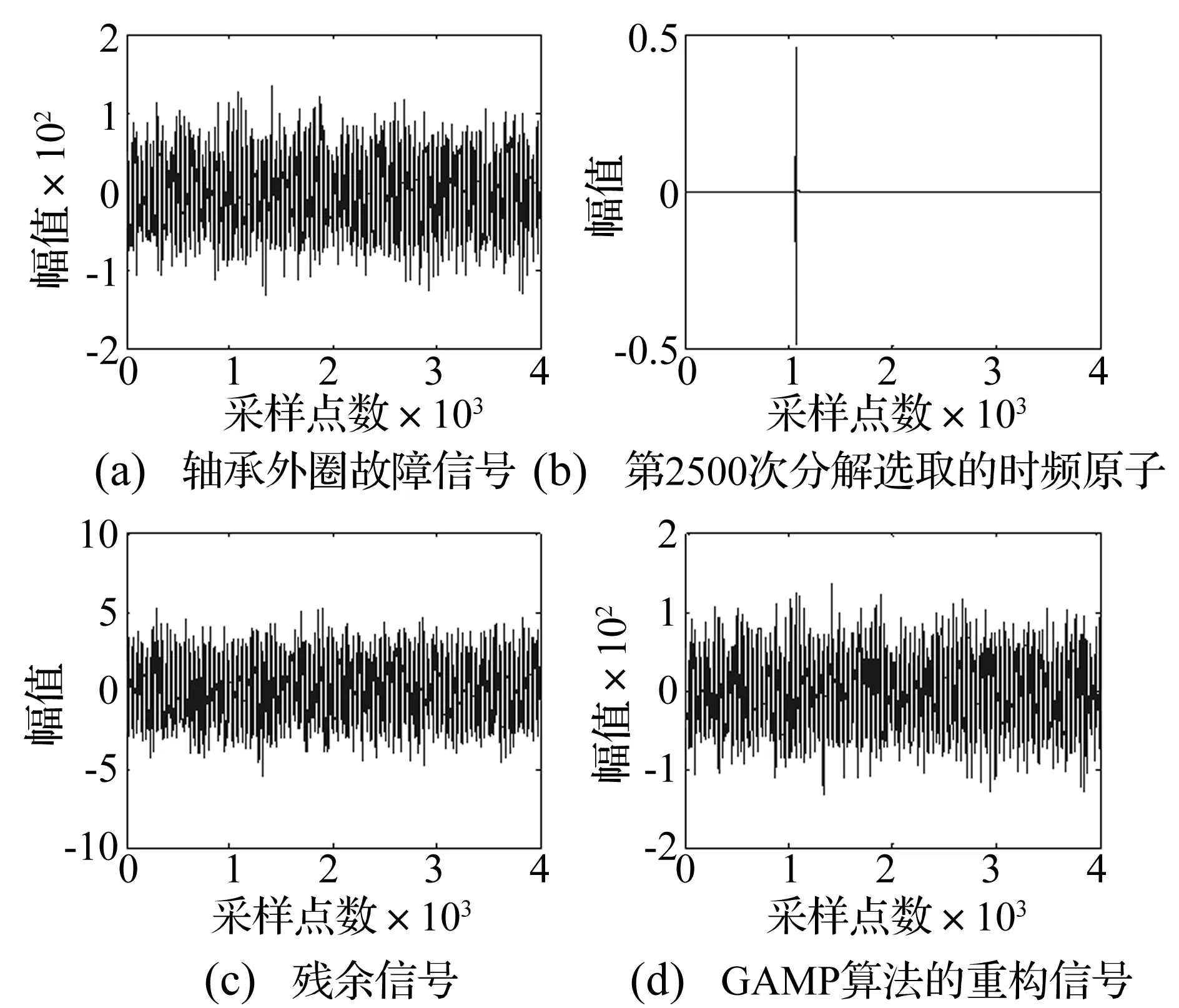
图12 经GAMP分解消噪的轴承外圈故障信号Fig.12 4 Bearing outer ring fault signal after GAMP decomposition de-noising

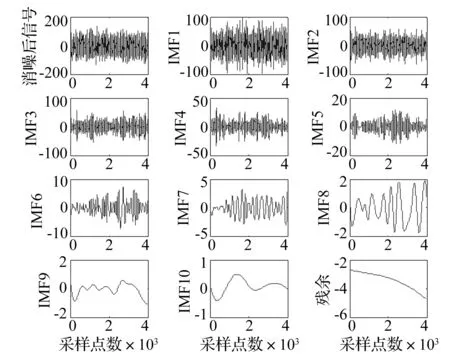
图13 EEMD分解消噪后的轴承外圈故障信号Fig.13 Bearing outer ring fault signal after EEMD decomposition de-noising

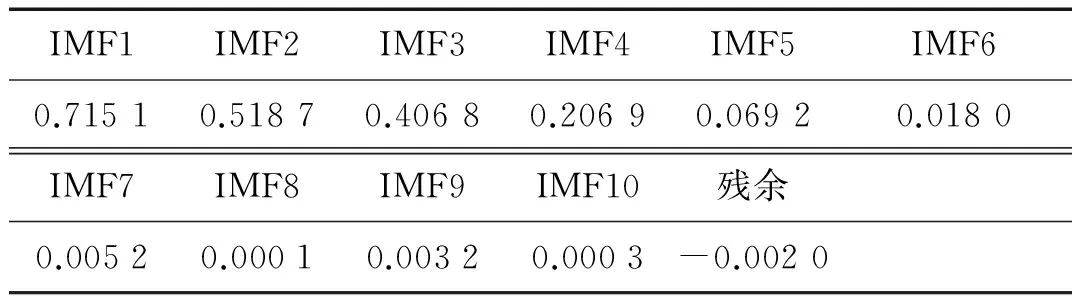
IMF1IMF2IMF3IMF4IMF5IMF60.71510.51870.40680.20690.06920.0180IMF7IMF8IMF9IMF10残余0.00520.00010.00320.0003-0.0020

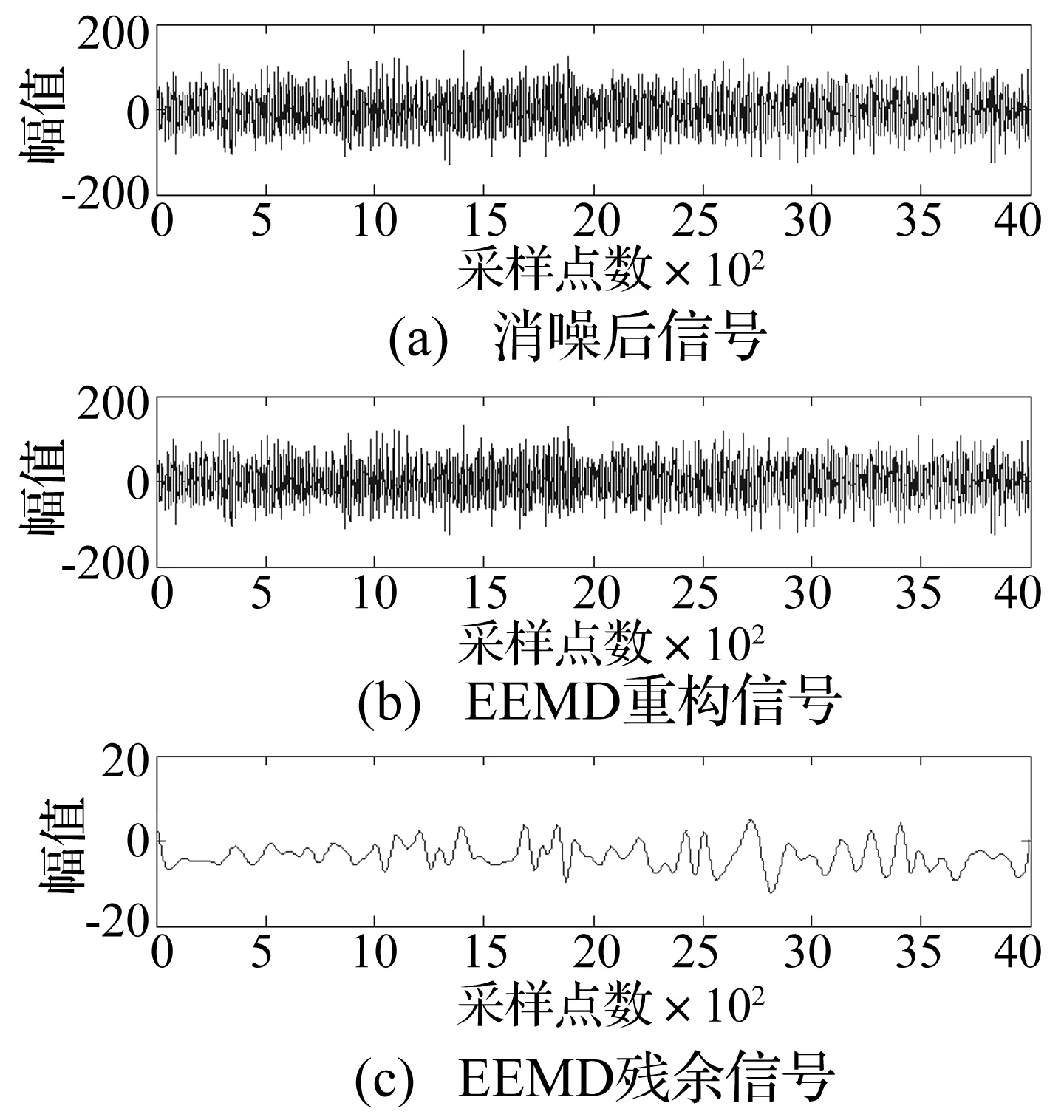
图14 EEMD分解后的重构信号与残差Fig.14 Reconstruction and residuals of EEMD decomposed signals

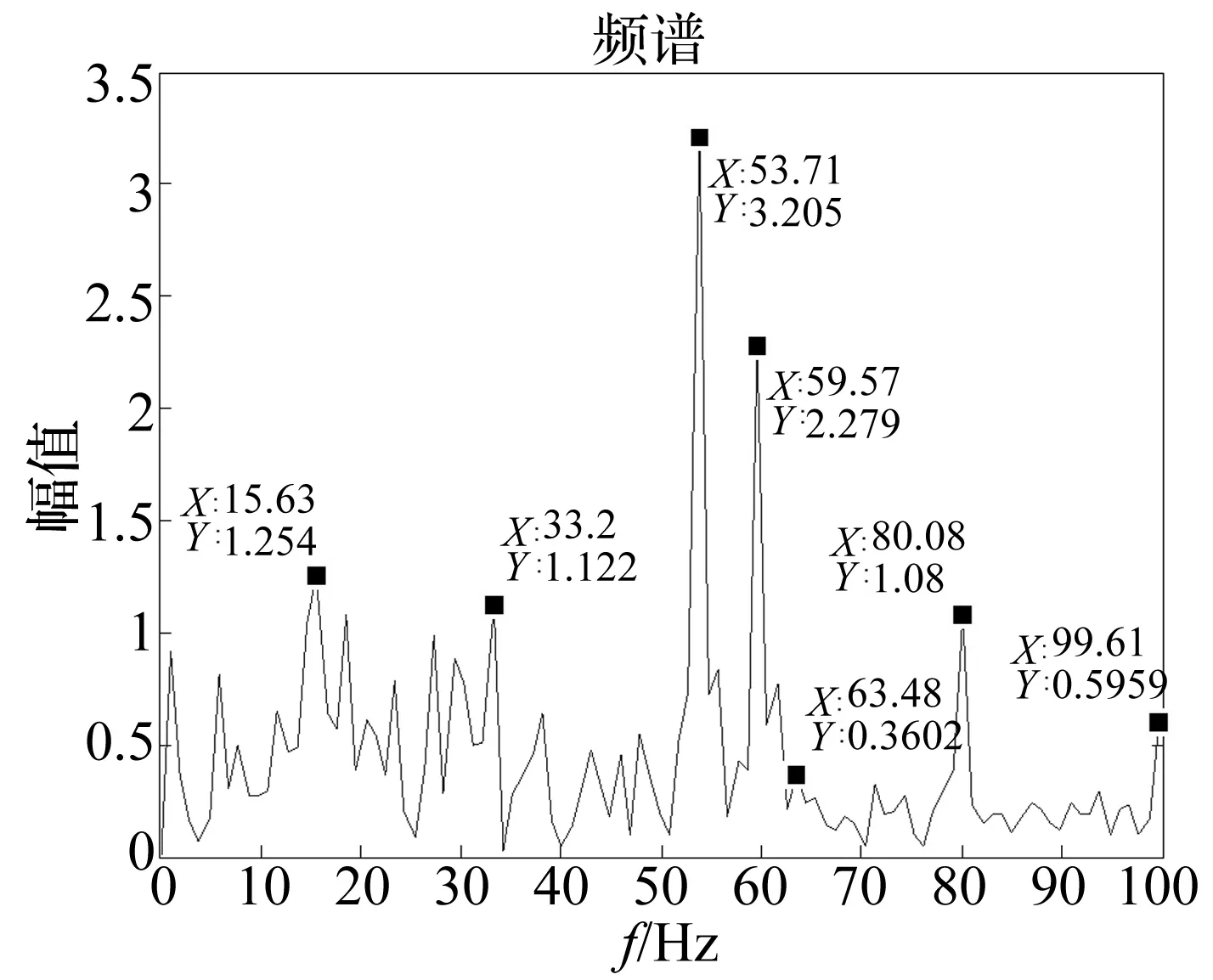
图15 重构信号的频谱Fig.15 Frequency spectrum of the reconstructed signal

图15中可以清楚的看到15.63 Hz、33.2 Hz、53.71 Hz、59.57 Hz、63.68 Hz、80.08 Hz、99.61 Hz以及其它频率成分，由表2可知，这些频率成分基本与齿轮啮合频率、输入轴转频、中间轴1转频、中间轴2转频和输出轴转频以及它们的倍频相对应，而33.2 Hz和99.61 Hz基本对应30309型轴承外圈故障频率32.86 Hz的一倍和三倍频，由此可以推测出轴承外圈发生了故障。

支持向量机(SVM)具有良好的分类性能，特别在小样本、非线性及高维特征空间中有较好的推广能力[10]。可采用此方法分类轴承的不同工况，便于后期的智能检测。将经过GAMP消噪和EEMD分解重构的正常和轴承外圈故障信号采用SVM进行分类，以800个数据点作为一个样本，提取的样本特征值为信号时域的有效值和均方差，信号频域的功率谱重心指标、均方频谱和谱原点矩。分类中，每种工况的20个样本生成训练集，10个样本生成测试集，设定正常工况的样本标签为1，轴承外圈故障的样本标签为2。每种工况10个样本的特征值生成测试集如表4所示。

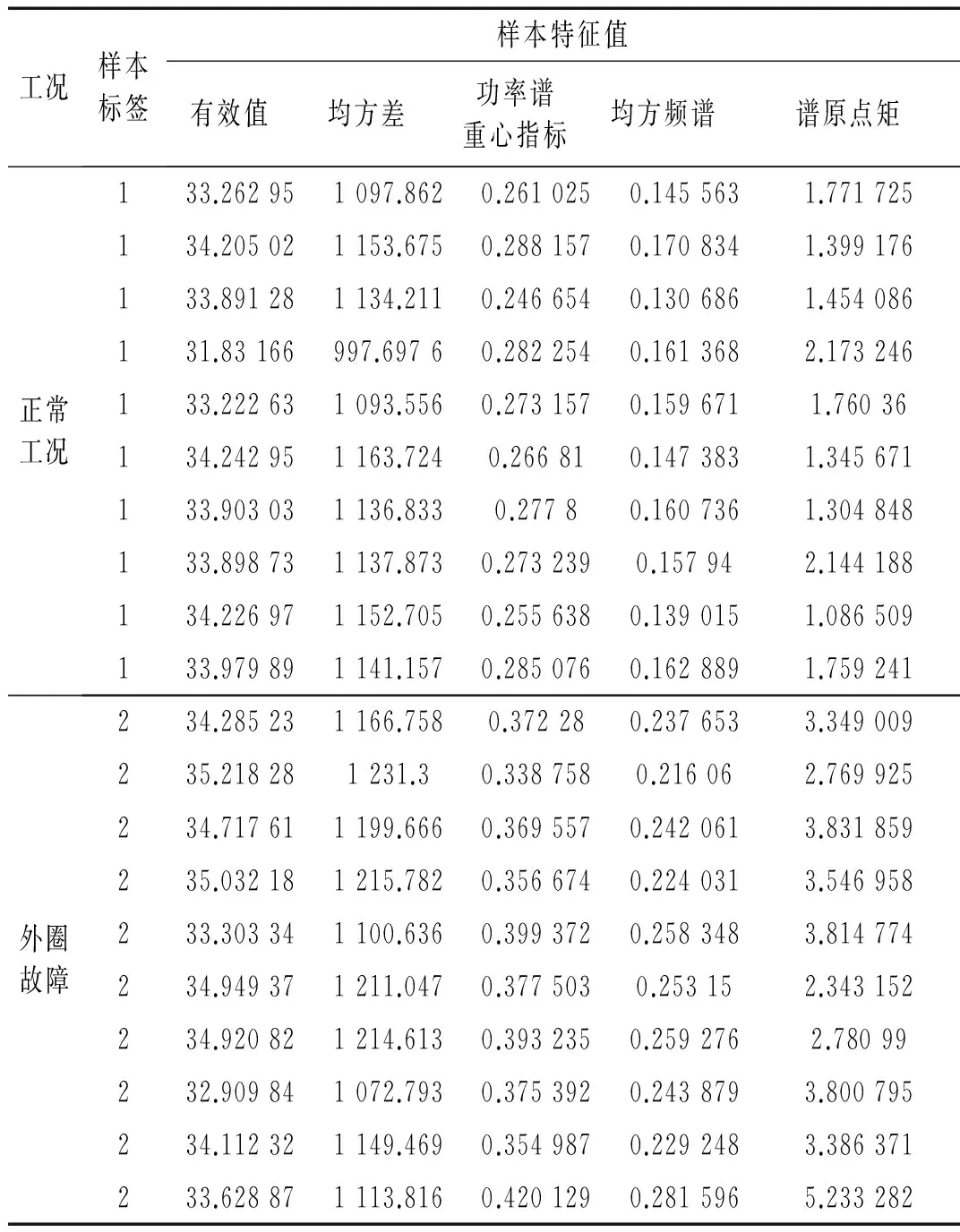
表4 测试集样本特征值

两种工况的训练样本和测试样本经过SVM训练和测试后得到的结果见图16。

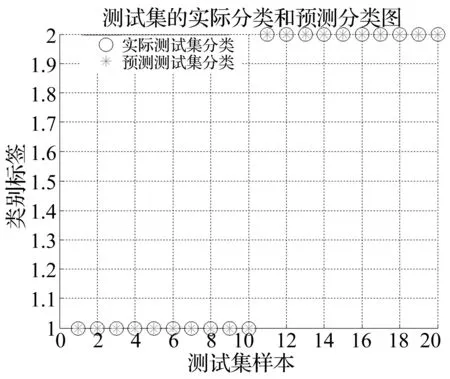
图16 两种工况SVM分类结果Fig.16 SVM classification results of two kinds of working condition

从图16可知，分类结果的正确率为100%，达到了很好的诊断效果。

5 结 论

本文采用基于遗传算法优化的匹配追踪算法(GAMP)和总体平均经验模式分解(EEMD)相结合的方法对滚动轴承振动信号的处理与分析。首先，利用GAMP算法将滚动轴承振动信号线性展开成能够较好匹配该信号特征结构的一系列高斯函数的叠加，消除了干扰噪声和锁定信号的局部特征；然后，利用EEMD方法剔除GAMP消噪后的振动信号中可能存在的虚假频率成分或不连续的分量，通过傅里叶变换将处理后的振动信号从时域转化到频域，提取出了故障振动信号的故障频率；最后，提取出经过GAMP消噪和EEMD分解重构的正常和轴承外圈故障信号的时域和频域特征值，采用支持向量机(SVM)进行分类，达到了很好的分类效果，实现了对滚动轴承的故障诊断。

[1] 杨宇，于德介，程军圣. 基于Hilbert边际谱的滚动轴承故障诊断方法[J]. 振动与冲击，2005，24(1):70-72.

YANG Yu, YU Deijie, CHENG Junsheng. Rolling bearing fault diagnosis method based on Hilbert marginal spectrum[J]. Journal of Vibration and Shock,2005, 24(1): 70-72.

[2] 陶少飞. 匹配追踪算法的优化及其在滚动轴承故障诊断中的应用[D].上海：上海交通大学，2012.

[3] 康晨晖，催玲丽，王婧，等. 基于信号特征的复合字典多原子匹配算法研究[J]. 机械工程学报，2012，48(12):1-6.

KANG Chenhui, CUI Lingli, WANG Jing, et al. Research of composite dictionary polyatomic matching algorithm based on signal feature [J]. Journal of Mechanical Engineering,2012，48(12):1-6.

[4] MALLAT S. A wavelet tour of signal processing[M]. San Diego, CA: Academic Press, 1988.

[5] FERREIRA DA SILVA A R. Atomic decomposition with evolutionary pursuit[J]. Digital Signal Processing, 2003, 13:317-337.

[6] PENG Z K, TSE P W, CHU F L. An improved Hilbert-Huang transform and its application in vibration signal analysis[J].Journal of Sound and Vibration, 2005, 286(9):187-205.

[7] ZHANG J, YAN R, FENG Z. Performance enhancement of ensemble empirical mode decomposition[J]. Mechanical Systems and Signal Processing, 2010, 24(7):2104-2123.

[8] 沈长青, 谢伟达, 朱忠奎, 等. 基于EEMD和改进的形态滤波方法的轴承故障诊断研究[J]. 振动与冲击，2013, 32(2):39-43

SHEN Changqing, XIE Weida, ZHU Zhongkui, et al. Rolling element bearing fault diagnosis based on EEMD and improved morphological filtering method[J]. Journal of Vibration and Shock, 2013, 32,(2): 39-43.

[9] 周智，朱永生，张优云，等. 基于EEMD和共振解调的滚动轴承自适应故障诊断[J]. 振动与冲击，2013，32(2):76-80.

ZHOU Zhi, ZHU Yongsheng, ZHANG Youyun, et al. Rolling bearing adaptive fault diagnosis based on EEMD and resonance demodulation[J]. Journal of Vibration and Shock, 2013, 32,(2): 76-80.

[10] 于湘涛，褚福磊，郝如江. 基于柔性形态滤波和支持向量机的滚动轴承故障诊断方法[J]. 机械工程学报，2009，45(7):75-80.

YU Xiangtao, CHU Fulei, HAO Rujiang. Fault diagnosis approach for rolling bearing based on support vector machine and soft morphological filters[J]. Journal of Mechanical Engineering, 2009, 45(7):75-80.

Rolling bearing fault diagnosis based on GAMP and EEMD

PAN Hongxia, ZHANG Xiang

(Institute of System Identification and Diagnosis Technology, North University of China, Taiyuan 030051, China)

Based on genetic algorithm to optimize the matching pursuit algorithm (GAMP) and ensemble empirical mode decomposition (EEMD), a rolling bearing fault diagnosis method was proposed. It could achieve the purpose of processing and analyzing rolling bearing vibration signals which had the characteristics of complex components and strong non-stationary in the experiment. First, the rolling bearing vibration signals were linearly expanded into a series of Gaussian functions which matched characteristic structure of signals by GAMP algorithm better. The purpose of eliminating interference noise and locking the local characteristics of the signals was achieved. Second, EEMD method was used to eliminate the false frequency components and discontinuous components that might exist in the vibration signals of GAMP. The processed vibration signals were transformed from the time domain to the frequency domain by FFT, and the fault frequency of the fault vibration signals was extracted. At last, support vector machine (SVM) was used to classify the normal and fault vibration signals of the rolling bearing, and the rolling bearings fault was diagnosed.

genetic algorithm match pursuit (GAMP); ensemble empirical mode decomposition (EEMD); support vector machine (SVM); rolling bearings；fault diagnosis

国家自然科学基金项目(50875247;51175480)

2015-03-26 修改稿收到日期：2015-09-25

潘宏侠 男，教授，博士生导师，1950年10月生

TH17；TG65

A

10.13465/j.cnki.jvs.2016.20.031