水平矩形沸腾通道的流量漂移模拟

张　翱

（华中科技大学能源与动力工程学院湖北武汉430074）

水平矩形沸腾通道的流量漂移模拟

张翱

（华中科技大学能源与动力工程学院湖北武汉430074）

对沸腾通道的压降特性进行了理论建模，并以动量差分方程为基础，对水平矩形沸腾通道的流量漂移现象进行模拟，研究了在不同的初始扰动下各个平衡运行点的流量漂移情况。结果表明：对于稳定运行点，无论初始扰动是正是负，系统都会回到初始运行点；随着初始扰动绝对值的增大，系统回到初始运行点所需的时间增加。对于不稳定运行点，如果初始扰动为正值，流量会一直增大并最终漂移到新的平衡运行点；如果初始扰动为负值，流量会一直减小并最终漂移到新的平衡运行点；随着初始扰动绝对值的减小，系统漂移到新的平衡运行点所需的时间增加。

沸腾通道；流量漂移；模拟

1　前言

近年来，工业设备热流密度的不断提高促使着人们寻求更高效的换热方式。流动沸腾换热由于利用了工质的相变潜热而具有极高的换热能力，因此被广泛应用于能源、动力、化工以及航天等高热流密度领域。然而，流动沸腾过程中容易发生各种不稳定现象，这些不稳定性不仅会降低设备的运行性能，还会危及设备的安全[1]。

在各种不稳定性中，流量漂移是文献中研究得较多的一种。流量漂移又叫Ledinegg不稳定性，其特征是受扰动的流体流动偏离原来的流体动力平衡工况，在新的流量值下重新稳定运行[1]。如果流量漂移导致流量减小，将会对沸腾通道造成极大危害，可能会引起烧坏[1]。很多学者对流量漂移进行了理论、实验以及模拟等方面的研究[2-6]。

本文首先对沸腾通道的压降特性进行了理论建模，其中两相区摩擦压降采用分相模型计算；然后对沸腾通道的动量方程进行离散，得到差分方程；最后以水为工质对水平矩形沸腾通道的流量漂移现象进行模拟，研究了在不同的初始扰动下各个平衡运行点的流量漂移情况。

2　理论模型

沸腾通道的压降ΔP包括单相液体区压降、两相区压降和单相气体区压降三个部分：

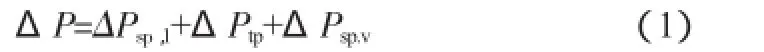
式中：ΔPsp,l为单相液体区压降；ΔPtp为两相区压降；ΔPsp,v为单相气体区压降。

以热平衡含气率xe=0作为单相液体区与两相区的分界点，以xe=1作为两相区与单相气体区的分界点。热平衡含气率xe由下式计算：

式中：h为通道截面上流体的焓；hl,sat为饱和水的焓；hfg为相变潜热。

通道截面上流体的焓h可以根据能量守恒得到：

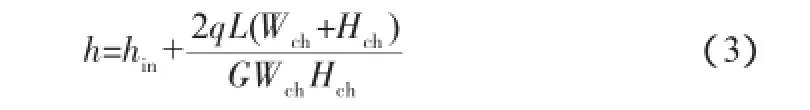
式中：hin为通道进口流体的焓；q为壁面热流密度；L为通道进口到流体焓值计算处的距离；Wch为通道宽度；Hch为通道高度；G为质量流速。

2.1单相液体区压降

单相液体区压降ΔPsp,l由下式计算：

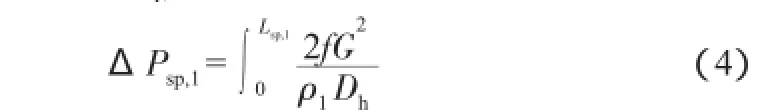
式中：Lsp,l为单相液体区长度；f为摩擦因子；ρl为液相比容，Dh为通道水力直径。

层流流动时，摩擦因子f由下式计算：

湍流流动时，摩擦因子f由Blasius方程计算[1]：

2.2两相区压降

对于水平通道，两相区压降ΔPtp包括摩擦压降ΔPf和加速压降ΔPa：

摩擦压降ΔPf采用Lockhart-Martinelli关系式[7]计算：

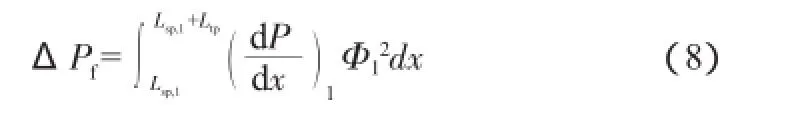
式中：Ltp为两相区长度；(dP/dx)l为液相单独在管内流动时的摩擦压降梯度；为分液相摩擦乘子，由Chisholm拟合公式[8]计算：

式中：C为与流动组合类型有关的常数；参数X的计算式为：

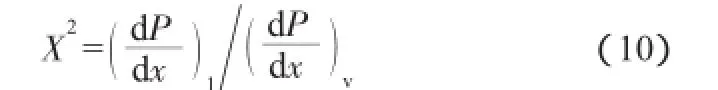
式中：(dP/dx)v为气相单独在管内流动时的摩擦压降梯度。

加速压降ΔPa由下式计算[1]：

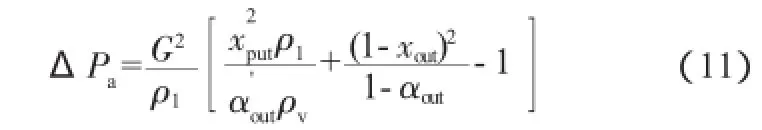
式中：xout为两相区末端的质量含气率；αout为两相区末端的截面含气率；ρv为气相密度。

截面含气率α由下式计算[9]：

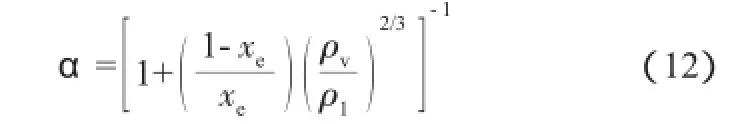
2.3单相气体区压降

单相气体区压降ΔPsp,v由下式计算：

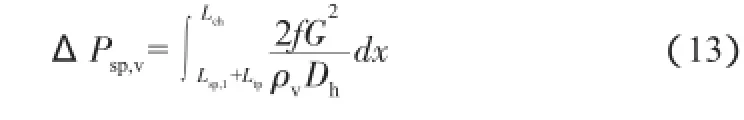
式中：Lch为通道长度；摩擦因子f的计算方法与单相液体区相同。

3　动量差分方程

沸腾通道的动量守恒方程为[10]：

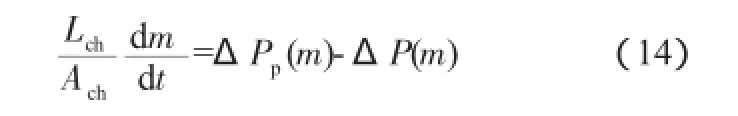
式中：Ach为通道横截面积；m为质量流量；ΔPp(m)为泵的压头；ΔP(m)为通道的压降。

假设初始平衡运行点的质量流量为m0，扰动为Δmt，则质量流量可表示为：

将式(15)带入式(14)可得：

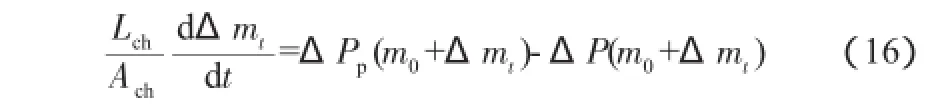
将式(16)进行离散化可得：

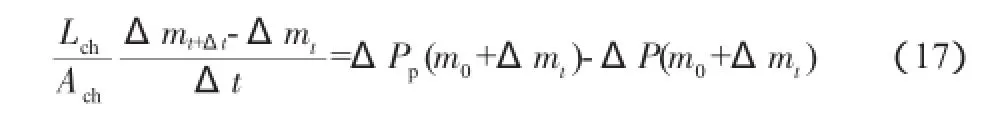
整理得：

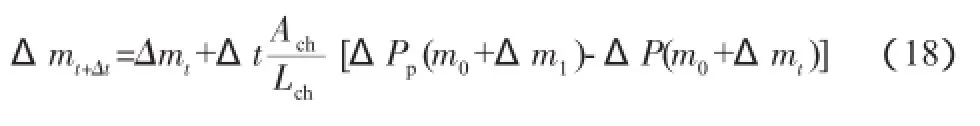
4　结果与分析

4.1计算模型

计算模型如图1所示。各个参数为：通道宽度Wch=1cm，通道高度Hch=3cm，通道长度Lch=3m，流体进口温度Tf,in=70℃，出口压力Pout=3Mpa，热流密度q=200W/cm2，工质为水。

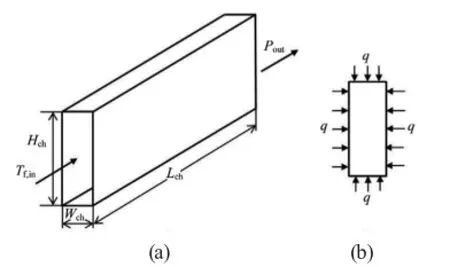
图1　(a)通道几何结构，(b)通道横截面热流分布

4.2沸腾通道各区域长度

图2为沸腾通道中各区域长度随质量流量的变化情况。随着质量流量的增大，单相气体区长度减小，单相液体区和两相区长度增大，当质量流量为0.192kg/s时，单相气体区消失。之后随着质量流量的继续增大，两相区长度减小，单相液体区长度增大，当质量流量为0.66kg/s时，两相区消失，通道中全是单相液体。

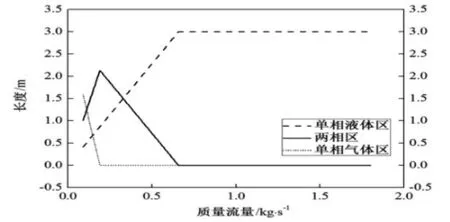
图2　沸腾通道中各区域长度随质量流量的变化

4.3沸腾通道压降特性

图3中的曲线a为沸腾通道的压降-流量曲线。随着质量流量的增大，通道的压降呈现先增大后减小再增大的变化趋势，呈N型。假设泵的压头不随流量变化，压头大小为30000Pa（如曲线b所示），则泵的压头-流量曲线与通道的压降-流量曲线有3个交点，这3个交点为系统的平衡运行点，对应的质量流量分别为0.1453kg/s、0.4227 kg/s和1.2976 kg/s。其中1点和2点的质量流量差为0.2774 kg/s，2点和3点的质量流量差为0.8749 kg/s。

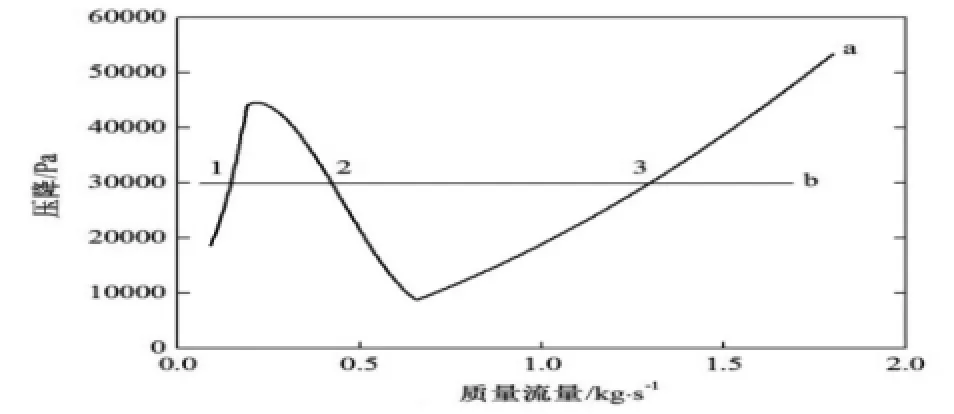
图3　沸腾通道的压降-流量曲线

4.4沸腾通道流量漂移的模拟

当系统的初始平衡运行点为1点时，在不同的初始扰动Δm0下，扰动随时间的变化情况如图4所示。无论初始扰动是正是负，扰动最终都趋于零，表明1点为稳定运行点，这可以通过图3来解释。由图3可知，在1点处，若扰动为正，则通道压降增大，导致驱动压头不足，因此流量减小，直到回到原来的运行状态；同理若扰动为负，则通道压降减小，驱动压头大于通道压降，使得流量增大，也会使系统回到原来的运行状态。由图4还可以看出，随着初始扰动绝对值的增大，系统回到原来的运行状态所需的时间增加。

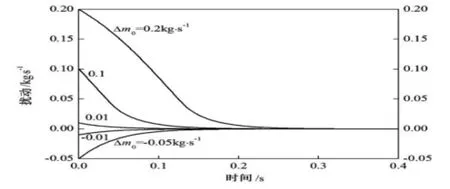
图4　1点处扰动随时间的变化

当系统的初始平衡运行点为2点时，在不同的初始扰动Δm0下，扰动随时间的变化情况如图5所示。在图5(a)中，初始扰动为正值，可以看到，无论初始扰动多大，随着时间的变化，扰动会不断增大并最终稳定在0.8749 kg/s左右。在图5(b)中，初始扰动为负值，同样可以看到，无论初始扰动多大，随着时间的变化，扰动会不断“增大”并最终稳定在0.2774 kg/s左右。因此，在2点处，如果初始扰动为正值，流量会一直增大并最终漂移到3点处；如果初始扰动为负值，流量会一直减小并最终漂移到1点处。由图5(a)和5(b)还可以看出，随着初始扰动绝对值的减小，系统漂移到新的平衡运行点所需的时间增加。

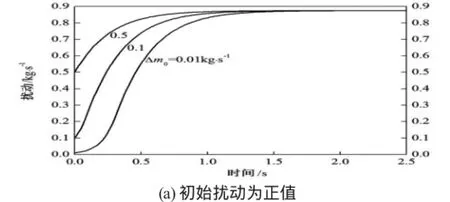
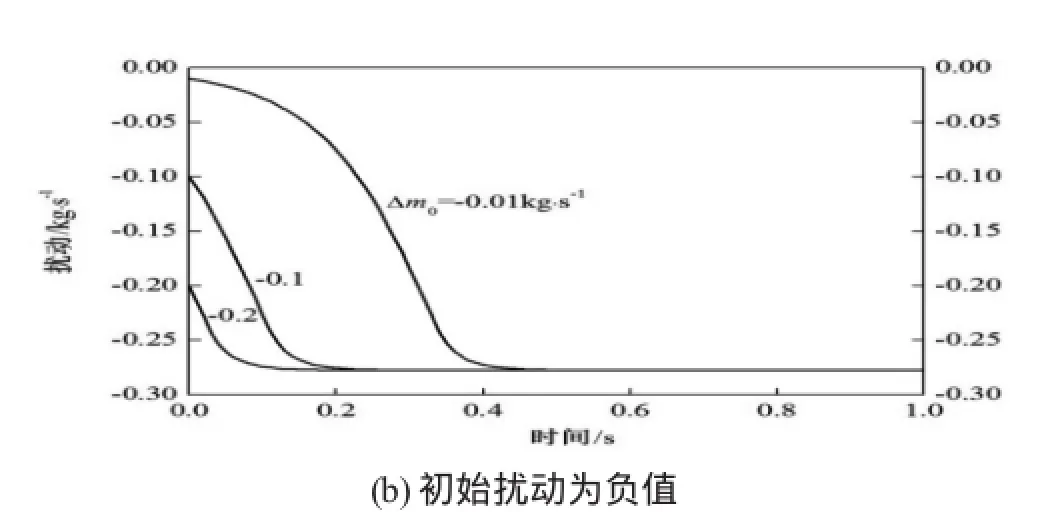
图5　2点处扰动随时间的变化

当系统的初始平衡运行点为3点时，在不同的初始扰动Δm0下，扰动随时间的变化情况如图6所示。与1点一样，3点是稳定运行点，且随着初始扰动绝对值的增大，系统回到原来的运行状态所需的时间增加。

图6　3点处扰动随时间的变化

5　结语

5.1对于稳定运行点，无论初始扰动是正是负，系统都会回到初始运行点；随着初始扰动绝对值的增大，系统回到初始运行点所需的时间增加。

5.2对于不稳定运行点，如果初始扰动为正值，流量会一直增大并最终漂移到新的平衡运行点；如果初始扰动为负值，流量会一直减小并最终漂移到新的平衡运行点。随着初始扰动绝对值的减小，系统漂移到新的平衡运行点所需的时间增加。

[1]徐济鋆,贾斗南.沸腾传热和气液两相流[M].北京:原子能出版社, 2001.

[2]Minzer U,Barnea D,Taitel Y.Flow rate distribution in evaporating parallel pipes—modeling and experimental[J].Chemical engineering science,2006,61(22):7249-7259.

[3]Zhang T,Tong T,Chang J Y,et al.Ledinegg instability in microchannels[J].International Journal ofHeat and Mass Transfer,2009, 52(25):5661-5674.

[4]Ruspini L C,Dorao C A,Fernandino M.Dynamic simulation of Ledinegginstability[J].Journal ofNatural Gas Science and Engineering, 2010,2(5):211-216.

[5]王少武,夏庚磊,彭敏俊,等.平行通道流动不稳定性研究[J].原子能科学技术,2012,46(10):1193-1196.

[6]陈冲,高璞珍,谭思超,等.窄矩形通道内Ledinegg不稳定性实验研究[J].原子能科学技术,2014,48(8):1411-1415.

[7]Lockhart R W,Martinelli R C.Proposed correlation of data for isothermal two-phase,two-component flowin pipes[J].Chemical EngineeringProgress,1949,45(1):39-48.

[8]ChisholmD.A theoretical basis for the Lockhart-Martinelli correlation for two-phase flow[J].International Journal of Heat and Mass Transfer,1967,10(12):1767-1778.

[9]Zivi SM.Estimation ofsteady-state steamvoid-fraction bymeans of the principle ofminimum entropy production[J].Journal ofHeat Transfer,1964,86(2),247-251.

[10]Zhang T J,Wen J T,Julius A,et al.Stability analysis and maldistribution control of two-phase flow in parallel evaporating channels[J]. International Journal of Heat and Mass Transfer,2011,54(25): 5298-5305.