基于改进多目标遗传算法的船闸调度方法

冯明波

(南通航运职业技术学院，江苏 南通 226010)



基于改进多目标遗传算法的船闸调度方法

冯明波

(南通航运职业技术学院，江苏 南通 226010)

针对目前我国内河航运船闸调度采用手工编制调度计划方式速度慢、调度水平低、缺乏科学性的现状，通过对单闸多目标调度问题进行建模，并基于改进的SPEA设计了模型求解算法，对船闸调度系统进行优化，为提高船闸通航能力提供了技术支持。

船闸；多目标调度；遗传算法

0 引言

目前我国内河航运的船闸调度基本采用手工编制调度计划的方式，调度计划编制速度慢、调度水平低、缺乏科学性，从而导致船闸使用效率低下，使得本就存在的船闸资源稀缺与航运总量急升之间的矛盾日益加大，极大地制约了我国内河航运的发展步伐。本文对内河航运船闸调度方法进行研究，建立调度问题的数学模型，并基于对调度方案的多角度考虑提出针对调度模型的多目标调度求解算法。

1 多目标船闸调度模型

船闸调度问题可以描述为：在特定时间段内，有若干船舶提出通过船闸申请，调度问题即是在现有船闸空间有限的前提下，合理为每一艘船舶安排通过船闸的时间和空间，从而达到减少船舶等候时间、提高船闸利用效率等目标。

根据调度问题中包含船闸的数量，该调度问题可分为单闸调度和多闸调度，本文主要针对单闸调度展开研究。根据调度范围的时间特性，船闸调度问题可分为静态调度和动态调度，本文针对静态调度问题进行研究。

在对船闸调度问题进行建模时，需要考虑以下问题：

(1)为了简化问题，本文将所有船舶视为矩形状且有方向性，即船舶的头部必须向前。船闸同样定义为矩形形状。

(2)为了规避船舶之间潜在的碰撞风险，为每艘船舶定义一个安全区域，即其船身(实际为其对应的矩形框)向外扩展一定的区域，在该区域内不可以安置其他船舶。对于不同的船舶类型，其安全区域大小不同。

(3)待调度船舶具有不同的身份：包含必须在本调度周期安排过闸的船舶(如特殊身份船舶)和一般船舶；包含经过前期多次调度仍未安排过闸的船舶以及本次调度前新加入的船舶。

1.1 变量与符号定义

(1)船闸调度问题所需的符号定义

M：待调度船舶数量；

nc：本调度周期包含的调度闸次数量；

Ll、Wl：船闸矩形的长、宽；

li、wi：船舶i矩形的长、宽；

ldi、wdi：船舶i的安全区域的长、宽；

wti：本调度周期起始时刻船舶i已经等待的时间；

wtiMAX：船舶i允许的最长等待时间；

I：必须在本调度周期安排过闸的船舶序号集合，包括特殊身份船舶和等待时间已经超过规定时限的船舶；

Tc：一个闸次的时间，假设每个闸次的执行时间相等，即Tc为一固定值。

(2)该调度问题的决策变量

xi,j：船舶i在闸次j中安排在船闸中的X坐标；

yi,j：船舶i在闸次j中安排在船闸中的Y坐标；

flagi：船舶i在本调度周期是否被调度标识。

上述变量中，xi,j和yi,j分别为船舶左下角点相对于船闸坐标系的X、Y坐标值。船闸坐标定义为：以船闸的左下角点为原点，与船舶按规定停泊后的头尾连线平行的方向为Y轴，船舶横向方向为X轴。

1.2 约束条件

船闸调度问题的约束条件如下：

xi,j∈{-1,[0,Wl]}

(1)

yi,j∈{-1,[0,Ll]}

(2)

(3)

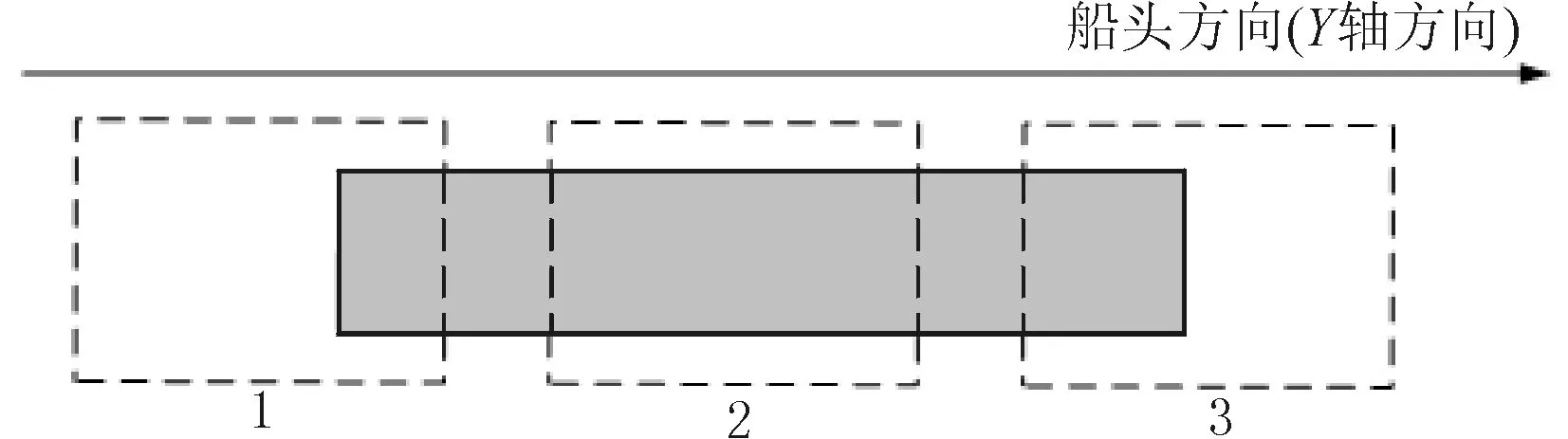
xi,j+wi+wdi

(4)

yi,j+li+ldi

(5)

∀i∈Iflagi=1

(6)

(7)

(8)

∀i1,i2∈{1,2,…,M} if (i1≠i2)∧(∃j st.

(9)

(10)

(11)

式(9)中定义的Overlapi1,i2表示在同一闸次内调度的两艘船舶i1和i2是否存在重叠的标识，其计算比较复杂，以下给出详细计算过程：

为简化分析过程，假定以船舶i1为参照，判断船舶i2是否与其有重叠区域。两船重叠分为2种情况，以船舶i2矩形的4个角点是否至少有1个落入船舶i1矩形区域内进行划分，如式(12)所示：

if (LDIni1,i2)∨(LUIni1,i2)∨(RDIni1,i2)∨

(RUIni1,i2)∨(WInci1,i2)∨(LInci1,i2)∨(AInci1,i2) then LDIni1,i2=true

else Overlapi1,i2=false

(12)

式中：LDIni1,i2、LUIni1,i2、RDIni1,i2、RUIni1,i2分别为判断船舶i2矩形左下角、左上角、右下角和右上角是否落入船舶i1矩形内的标识，可统一由下式确定：

if (xLDIni1,j

else PTlni1,i2=false

(13)

式中：xLDi,j、xRUi,j、yLDi,j和yRUi,j分别表示船舶i矩形的左下角和右上角点的X和Y坐标；xPTi2,j、yPTi2,j和PTIni1,i2为形式化变量，分别从{xLDi2,j, xLUi2,j, xRDi2,j, xRUi2,j}、{yLDi2,j,yLUi2,j,yRDi2,j, yRUi2,j}和{ LDIni1,i2，LUIni1,i2，RDIni1,i2，RUIni1,i2}中取值(3个变量取值序号一一对应)从而组成4个公式。其中xLUi,j、xRDi,j、yLUi,j和yRDi,j分别表示船舶i矩形的左上角和右下角点的X和Y坐标。

对于船舶i2矩形的4个角点均未落入船舶i1矩形区域内的情况，又分为2种情况：一是船舶i2在横向跨度(X方向)上包含i1在横向上的跨度区域(对应于式(12)的WInci1,i2)；二是船舶i2在纵向跨度(Y方向)上包含i1在纵向上的跨度区域(对应于式(12)的LInci1,i2)。如果2种情况均满足，则对应于船舶i2将船舶i1包含在其矩形框内(对应于式(12)的AInci1,i2)。而情况1与情况2的区别仅在于判断方向为X轴还是Y轴，因此下面仅以情况1(即WInci1,i2的计算)为例展开分析。满足情况1的两船关系又分为4种情形，其中3种情形如图1所示(第4种情形为船舶i2将船舶i1包含在其矩形框内)。图中实形框为船舶i1，3个虚形框分别对应于3种情形下船舶i2的位置。这3种情形可统一描述为：在Y轴方向，只要船舶i2的左下角点或者右上角点位于船舶i1的左下角点和右上角点之间即可，因此可由下式确定：

图1 船舶i2横向跨越船舶i1时两者重叠情况示意图

(14)

而船舶i2在横向跨度(X方向)上包含船舶i1在横向上的跨度区域的判断条件为：

(15)

(16)

同理：

xRUi2,j

(17)

在以上计算WInci1,i2和LInci1,i2的公式中均忽略了船舶i2将船舶i1包含在其矩形框内的情形，因此需单独计算AInci1,i2：

AInci1,i2=(xLDi1,j>xLDi2,j)∧(yLDi1,j>

yLDi2,j)∧(xRUi1,jyRUi2,j)

(18)

由此，两船重叠判断式(12)所需条件均可计算得出。

1.3 调度指标

考虑以下2个船闸调度指标：

一个是从用户的角度出发，要求所有船舶的等待调度时间尽量短。为了简便计算，在此仅考虑船舶在本调度周期内等待的时间：

(19)

另一个是从交通管理部门的角度出发要求更高的通过率，因此要求在当前调度周期内安排尽量多的船舶过闸：

(20)

2 多目标船闸调度算法

本文建立的船闸调度模型是典型的NP-hard问题，目前遗传算法、蚁群算法和粒子群算法等智能搜索算法在该类问题的求解得到了广泛应用并取得了良好的效果。本文建立的船闸调度模型是一个多目标调度问题，针对这类问题一种简单的方式是采用加权求和的方式将多目标调度转化成单目标调度问题，但是正如上一节所介绍，本调度问题所提出的2个指标分别从航运管理部门和用户角度出发，二者之间在某种程度上存在一定的冲突，难以确定相对权值，该方法存在一定限制。目前针对多目标调度问题应用比较多的是多目标遗传算法，如NPGA、NSGA和NSGA-II，以及SPEA和SPEA-II等[2-5]。其中SPEA基于Pareto支配理论进行设计，基于“支配个体所有Pareto解所支配个体的数量总和”这一隐含信息对个体周围的密度进行评价，能够避免设置其他算法涉及的小生境参数这一难题[6]。本文基于SPEA算法对多目标船闸调度问题进行求解。

2.1 算法流程

本文基于SPEA算法设计多目标船闸调度算法流程如图2所示。

2.2 染色体编码与种群初始化

定义染色体：s=[(j1,x1,j1,y1,j1),(j2,x2,j2,y2,j2),…, (jM,xM,jM,yM,jM)]，染色体包含M组基因，每组基因为1个三元组，对应于1艘船的调度闸次、在该闸次中安排在船闸的X和Y坐标。染色体长度为3×M，且基因取值-1的大幅度减少。在交叉和变异计算时，以1个三元组基因为单位进行。

图2 多目标船舶调度算法流程

在进行种群初始化时，要求生成1组对应于模型可行解的染色体，并且尽量使这些可行解具有较高指标，即对应于较优解，为后面的种群进化奠定较好基础。本文基于贪婪算法思想设计种群初始化策略，该策略生成1个染色体的过程如下：

step1:从待调度船舶集合中随机选取1艘船i；

step2:在剩余闸次的空间资源内对船舶i进行排闸；

step2.1：在未遍历闸次集合中随机选择1个闸次j；

step2.2：调取闸次j的已安排船舶集合Bj，基于式(9)判断船舶i是否可以安排进闸次j，如是则将船舶i加入集合Bj，并将船舶i安排的闸次j及在船闸中的坐标更新至染色体对应的位置中，进入step3；否则进入step2.3；

step2.3：未遍历闸次集合是否为空，如是则将染色体对应船舶i的基因三元组置为(-1,-1,-1)，并进入step3；否则将闸次j从未遍历闸次集合中去除并返回step2.1；

step3：将传播i从待调度船舶集合中去除。判断待调度船舶集合是否为空，如是则过程结束，输出染色体；否则返回step1。

上述过程反复执行N次，即可得到对应于N个可行解的染色体集合，即初始种群。由于该过程在选择船舶和闸次的过程中均为随机选取，因此可以产生不同的可行解。

2.3 主要遗传算子设计

2.3.1 适应值计算

本文对SPEA进行改进，提出个体适应值的计算方法。SPEA存在一个缺点，即容易产生适应值相同的个体，尤其针对几个相互接近而又不具有Pareto支配关系的个体，SPEA很难有效地区分它们的适应值[7]。这是因为SPEA在针对一个个体进行适应值计算式只考虑到支配该个体的Pareto解，而该个体所支配其他个体的情况并非被考虑，而后者是区分相似个体的重要因素，对此本文对SPEA的个体适应值计算方法进行改进如下：

(21)

式中：fitness(xi)为个体的适应值；PDStrSum(xi)为所有Pareto支配xi的个体的强度和(称为支配解强度和)；Str(xi)为xi的强度，即所有被xiPareto支配的个体数量；StrEqu(xi)为所有xi与具有相同支配解强度和的个体集合。

2.3.2 交叉和变异算子

交叉算子以两个个体相对应的一对三元组为单位执行。为了保持种群的多样性，针对三元组设计两种交叉模式：一种是整体交换，即将两艘船舶被安排的闸次和在闸坐标整体交换；另一种是局部交换，即不改变船舶的原调度闸次，仅交换在闸距离。针对个体I1和I2，交叉算子过程如下:

step1：在I1和I2上各随机选择基因三元组t1和t2；

step2：生成[0,1]之间的随机数，将该随机数与事先设定阈值比较，如随机数大则进入step3，否则进入step4；

step3：执行整体交换，即将t1放到I2上而将t2放到I1上，进入step5；

step4：执行局部交换，即将I1中t1上的后2个数组成的二元组与I2中t2上的后2个数组成的二元组进行交换，进入step5；

step5：针对交叉后的I1和I2上的三元组t1和t2进行微调，即加入较小随机数。

交叉过程的step5目的是进一步增加种群多样性，防止种群在船闸少数几个坐标点附近陷入局部解。为了进一步提高算法的解空间搜索能力，需进一步执行变异操作，变异算子与交叉算子的step5类似，只是加入的是一个较大随机数，并且在个体的每个三元组均执行变异操作。

算法执行完交叉和变异算子后得到新的种群，但是新种群中个体对应的解是否为可行解难以保证，因此要针对新种群的每一个个体进行可行化转化，即针对个体上每一个基因三元组对照上一节给出的约束条件组依次判断是否违反，如是，则将该三元组置为(-1，-1，-1)。

2.4 算法实例验证

本文基于VC6.0对提出的模型与算法进行了实现，算法运行在IntelCorei7 2.5GHz平台下，内存为4.0GB，操作系统为Win10。为了模拟多种规模的船舶调度问题，船舶数量和尺寸、船闸尺寸等在给定区间内随机取值。为了对算法进行验证，将该算法与基于“先到先服务”原则的贪婪算法进行比较，比较指标C设计如下：

C=PD1,2/PD2,1

(22)

2种算法同时运行K次，得到2组各K个调度结果，令本文设计的求解算法序号为1，贪婪算法序号为2，PDi,j表示算法i得到的K个调度结果中Pareto支配算法j得到的K个调度结果的个数之和。因此，C值越大表明算法1的性能越优于算法2。算法运行结果见表1。

表1 算法运行结果

由表1可以看出，在随机生成的6个实例中，C值均大于1，说明本文提出的算法相比贪婪算法具有明显的优势。

3 结论

本文针对现阶段我国内河船闸使用效率低下，导致本就存在的船闸资源稀缺与航运总量急升之间的矛盾日益明显，极大地制约了我国内河航运的发展步伐等问题，对内河航运船闸调度进行了研究；建立了该问题的调度约束满足的多目标船闸调度模型，并基于改进的SPEA设计了该多目标调度问题的求解算法；最后通过算法实例验证了该算法的可行性和有效性，为船闸调度系统优化、船闸的高效运行提供了建议方案和技术支持。

[1] 蔡恩泽. 内河水运“金”涛拍岸[J].决策与信息,2011(5)：35-37.

[2] 冯明月,李国辉,易先清，等. 一种求解多目标柔性JSP的正交遗传算法[J].系统仿真学报,2009,21(15)：4682-4690.

2016-04-13

江苏省交通运输科技项目(2014C03-05)

冯明波(1977—)，男，讲师，研究方向为轮机管理。

U641.7

A