基于有功功率解耦的高能量密度单相PWM整流器

王归新 陈海东 汤大猷 方 鑫 程 维

(三峡大学 新能源微电网湖北省协同创新中心， 湖北 宜昌 443002)



基于有功功率解耦的高能量密度单相PWM整流器

王归新 陈海东 汤大猷 方 鑫 程 维

(三峡大学 新能源微电网湖北省协同创新中心， 湖北 宜昌 443002)

单相PWM整流器直流侧含有2倍基波频率的纹波电能，输出电压随负载变化周期波动．传统方法采用无源滤波的方式，通过在直流侧添加大电容滤除低频谐波电流．但这种电容体积较大，不利于设计高能量密度的变换器．本文利用有功功率解耦的方法，利用直流电容存储纹波电能．可稳定输出电压，减小电容值．然后对控制策略进行研究，使用电压电流双闭环控制方法，实现系统快速响应和稳定特性．该方法通过仿真得到验证．

单相PWM整流器； 有功功率解耦； 纹波电能； 双闭环控制

单相PWM整流器广泛地运用于电力设备中，如不间断电源(UPS)、直流供电系统．它具有效率高和低谐波的特点．由于单相PWM整流器将电能由交流变为直流，输出的瞬时功率既含有一个直流分量又含有一个交流分量，且交流分量脉动频率为电网频率的2倍[1]．因为输出功率含有低频谐波电流，导致输出电压周期波动．随着负载功率的提升，电压纹波增大．为减少输出电压和输出功率的波动，就必须在直流侧接入大容量电容．虽然大电容能够抑制电压波动，使得输出功率平滑[2-6]．但它的体积较大[7]，使用寿命短．为了解决这些问题，文献[8]提出运用有功功率去耦合的方式，滤除输出功率的交流分量，实现输出电压的稳定．文献[9-13]介绍的几种电路拓扑利用电感或电容的储能特性，将波动的电能储存在储能元件中，减小直流侧电流波动，提高输出电压的稳定性．

图1(a)所示电路，利用电感储存纹波电能，通过调制Q5、Q6控制电感电流正弦，使电流交流分量流入滤波电感．既实现对输入电能的滤波功能，又对输出功率进行补偿．同时，由于输出电压稳定，可在直流侧采用小容量电容减小系统体积，提高系统稳定性．但是要使储能电感完全存储纹波电能，在电感大小一定的情况下，负载功率增大，流入电感纹波电流必然增大，这样才能确保滤除脉动功率，维持直流电压稳定．显然地，面对图1(a)电路中的问题，一种方法是增大储能电感容量，限制电流变化范围，但电感容量增大其体积也将增大，系统成本增加．而电感值较小，电感电流增大，电路损耗提高发热严重，同样不利于电路设计．所以尽管电感储能具有稳定耐用的特点，但还存在能量密度低的缺点．

图1(b)中辅助储能支路，采用电感电容串联的结构．电容作为储能元件，电感在电容和直流母线之间实现电能传输的作用，避免电容受直流母线电压冲击．当上桥臂Q5导通时，辅助支路工作于buck模式，电容和电感储能．当开关管Q5关断，电感电流由Q6体二极管续流．同理可知，当开关管Q6导通时，支路工作于boost模式，关断时由Q5体二极管续流向直流母线释放电能．由于电容储能的特性，提高电容电压可增加电容储能效率，同时也将减小电容充电电流．另外由于辅助支路工作于电流断续模式，电流存在尖峰．电容电压必须为正极性，电容利用效率低．

图(c)电路将LC支路与网侧相连，电容电压调制为正弦，电容利用效率高．图1(c)电路拓扑基本解决了有功功率解耦技术应用问题，但它的辅助电路控制系统计算复杂，而且需要高性能单片机．本文采用直流电容滤波的方式得到如图2所示电路，可减小电容、稳定直流电压和实现电能的双向流动．

图1 几种典型的基于有功功率解耦的单相PWM整流电路

图2 基于有功功率解耦的单相PWM电路

1 电路工作原理分析

本文提出单相PWM整流电路如图2所示．由主电路建立直流电压Udc，令C1=C2=Cf，同时用uc1(t)和uc2(t)代表上下电容电压．为了吸收直流电压上的2倍电网频率纹波，将uc1(t)和uc2(t)调制为正弦电压与直流母线电压一半之和．公式可写为：

(1)

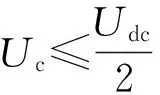
(2)

其中Ic为电容电流幅值．电容瞬时功率pc(t)可写为：

(3)

为了准确描述功率补偿大小，还需要考虑滤波电感Lf的瞬时功率pLf(t)，它的表达式为：

(4)

(5)

因此，辅助电路的主要瞬时功率pf(t)可表示为

(6)

假设电网电压如下

(7)

为实现单位功率因数输入，输入电流必须与电压同相位，则有电流为

(8)

输入瞬时功率可表示为

(9)

主电路电感L的瞬时功率可表示为

(10)

忽略变换器损耗，输入功率与输出功率相等．因此可得到等式为

(11)

由于负载功率稳定，所以有等式：

(12)

将式(6)、(9)、(10)和(12)代入式(11)得到

(13)

利用三角函数，对式(13)等式两边化简

(14)

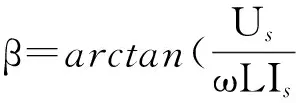
(15)

(16)

图3描述的各电量波形，忽略电感损耗、开关损耗和传输损耗．当主电路工作时，电感电流is跟踪网侧电压相位，实现单位功率因数运行．输入瞬时功率有2倍网侧基波频率的脉动功率，通过辅助支路补偿直流侧输出功率抵消功率脉动，使负载功率达到稳定．图3(c)所示，电容电压交流分量相互抵消，得到稳定直流电压．

图3 辅助电路工作时各电量波形

为了检测有功功率去耦合技术对电容容量的要求，计算电容纹波功率．电感瞬时功率占脉动功率比重较小，不考虑电感和电路损耗的影响．假设电容的脉动电压达到最大值Uc=Udc/2，此时电容利用效率最高．由式(13)忽略电感作用可得：

(17)

(18)

式中，Pload为负载功率且为纹波功率幅值．Ceq为直流侧等效电容．实际电路中直流母线电压不可能完全恒定，存在小范围波动．当辅助支路电容满足有功功率补偿要求时，可在直流侧串联电容，进一步减小电压纹波．

与传统单相PWM整流器相比，假设直流侧无脉动功率，同时电压纹波为额定电压的1%，脉动频率为网侧基波频率的2倍．直流电容的计算公式如下：

(19)

由公式可得，基于有功功率解耦的单相PWM整流器，其直流电容值为传统单相PWM整流器2/25．但在实际电路中，考虑到系统裕量．电压Uc最大值必须小于Udc/2保证电路正常运行．所以应当选择合适的Uc幅值．

2 系统的数学模型与控制策略

2.1 电路数学模型

单相PWM变换器控制策略较为成熟，在此不再赘述，只讨论辅助支路的控制策略．图4已给出辅助支路电路平均开关模型，电阻r表示等效的电感和电容损耗、开关死区效应．

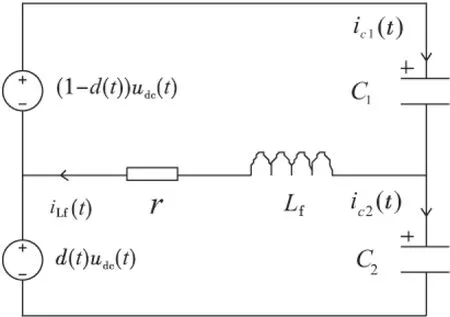
图4 辅助电路平均开关模型

根据图4列写不同回路的状态空间变量的开关周期平均值方程：

(20a)

(20b)

由等式(20a)、(20b)可得到不同变量的状态空间方程，因为系统的数学模型建立在理想的稳态条件下，所以引入电压uc(t)作为反馈量．由于在实际电路中，系统存在大量噪声和电磁干扰．如果单独依靠采样uc1(t)或c2(t)电压，经过变换得到的uc(t)反馈信号可能与实际值产生误差，影响系统的稳定性．故利用等式uc(t)=(uc2(t)-uc1(t))/2可减小采样误差信号带来的影响，使得到反馈信号更精确．因此，对等式(20a)、(20b)进行等效变换并化简为：

(21)

根据式(21)，用扰动法求解小信号交流模型．如果对输出电压udc(t)、电容电压交流分量uc(t)、占空比D和电感电流iLf(t)在直流工作点附近作为小扰动，即可得到扰动后状态空间平均方程：

(22)

根据稳态关系可知，等式(22)直流项之和为零．由于二阶交流项远小于一阶交流项，于是二阶交流项可忽略不计，式(22)化简为

(23)

系统工作时，因为扰动项udc(t)的幅值(0.5-D)远小于d(t)的幅值Udc，可忽略直流母线电压纹波扰动．对交流小信号模型进行拉氏变换，得到下列传递函数：

(24)

2.2 控制策略

采用电压环控制电容电压uc．因为被控变量为交流信号，为了消除静态误差选用比例谐振控制器(PR)．单一电压环控制结构易受电路纹波功率干扰，由于电压环很难快速跟踪参考值，反馈电压信号含有低频纹波，容易引起电压畸变，导致直流母线电压产生较大纹波．如图5所示，文中提出电压外环电流内环的控制结构．电压环控制电压uc幅值和相位，电流环快速地调整电感电流iLf，抑制电路谐波信号扰动，使电压uc能及时跟踪电压参考量．

图5 辅助电路控制结构图

其中，KPWM为桥路等效增益．为简化分析，暂不考虑uc的扰动，电流内环结构如图6所示．

图6 电流内环控制结构图

PR控制器角频率ωo为网侧基波角频率(ωo=314 rad/s)，角频率ωc用于调节控制器在谐振频率的增益和带宽，一般选择范围为5～15 rad/s．比例系数KPi控制系统增益，谐振系数KRi决定谐振频率处增益．根据图7所示PR控制器bode图，除在谐振点附近，其增益保值恒定．

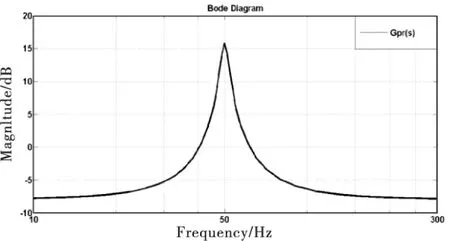
图7 传递函数bode图

电流内环中PR控制器可按P控制器进行整定，由于被控对象是工频电流，电流内环只需考虑满足对应50 Hz频率的开环增益Kg(Kg≥6 dB)，同时满足相位裕量γ(30°≤γ≤60°)．

(25)

考虑电流内环相位裕量γ，计算其开环传递函数的剪切频率ωc．

(26)

其中ω1=r/L．通过选择合适比例系数KPi满足系统裕量．PR控制器带宽ωc=10 rad/s，谐振系数KRi取值不影响系统裕量，此处取KRi=10．电压外环PR控制器参数整定与内环相似．在设计电压外环时，把内环作为控制对象，内环PR控制器传递函数近似为P控制器．外环整定方式与内环相似．首先整定外环KPv参数，满足系统裕量，然后确定谐振参数KRv．

如图8电流环bode图所示，系统在未加控制器校正时，工频频率开环增益为低．加入PR控制器提高了开环增益，可实现对交流信号的快速跟踪．从另一方面看，提高开环增益使得系统的相位裕量降低．在参数整定时，需要综合系统的开环增益和相位裕量，选择最优参数．

图8 电流环bode图

图9表明，系统未加入PR控制器时，低频段开环增益较低．加入PR控制器提高了系统增益，加快了系统的响应速度，同时进一步消除交流信号静态误差．从图中可得到，系统外环开环增益为9.6 dB，相位裕量为75°．显然采用双环控制结构，抑制了基波倍频的谐波信号，提高了系统响应速度．

图9 电压环bode图

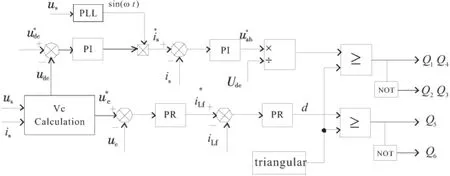
图10 系统控制结构框图

2.3 电路设计

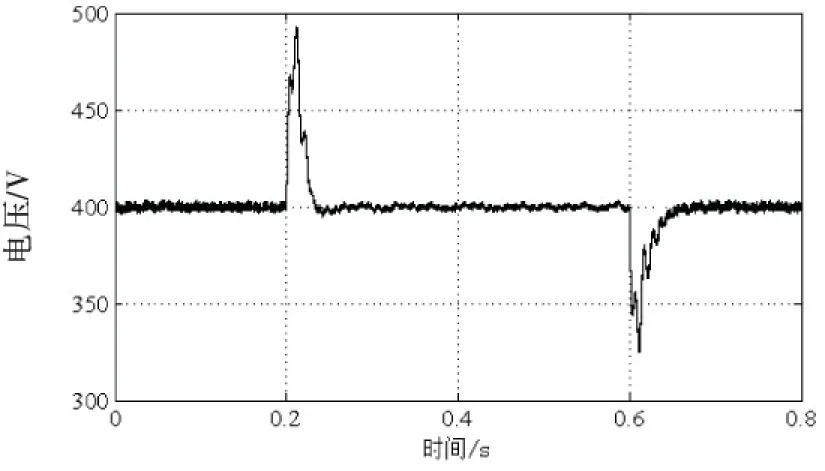
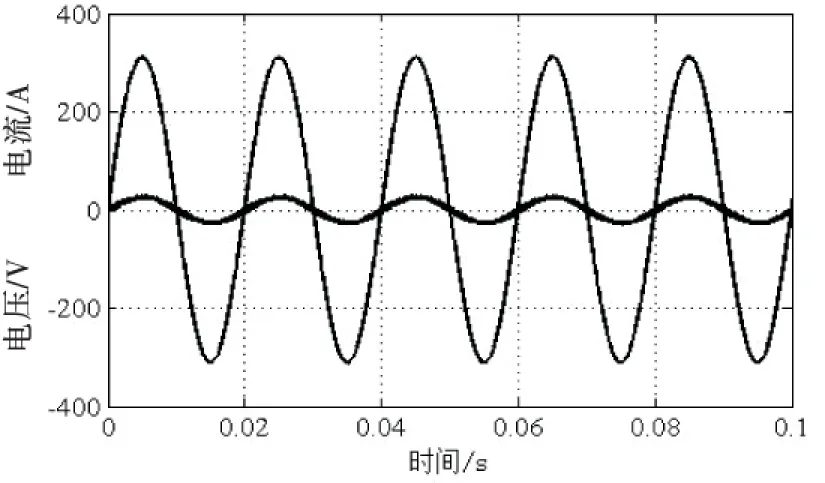
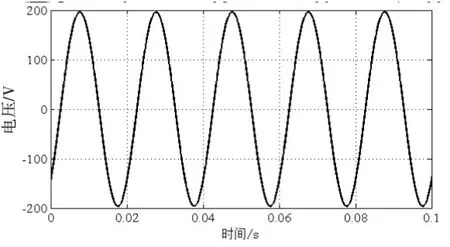
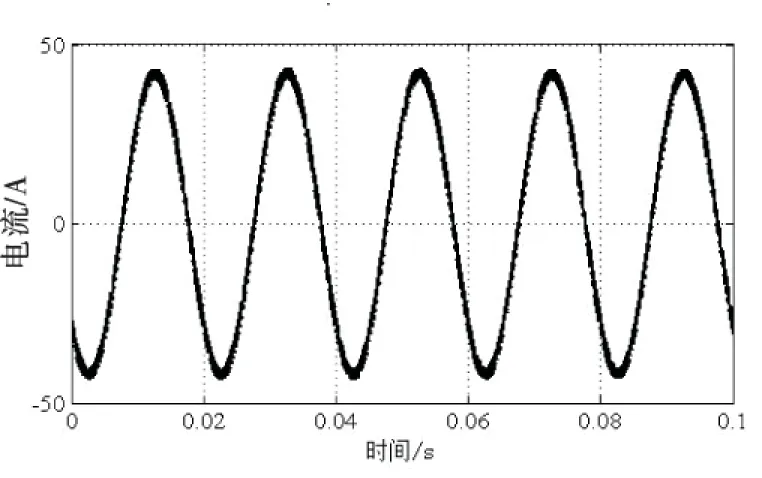
辅助支路电容可根据式(17)得到，只需考虑电感．假设开关频率fs较高，在一个开关周期内，电压uc幅值一定．忽略等效电阻r，当开关管Q5关断、Q6开通时，即在t∈(kTs≤ton

(27)

当开关管Q5开通、Q6关断时，即在t∈(kTs+DTs≤toff≤(k+1)Ts)范围内有

(28)

得到，电感电流纹波幅值有

(29)

系统稳定工作时，电感电流幅值为iLf=2ωCfUc．考虑极端情况，占空比D=1，且负载为额定功率时Uc的幅值．电流纹波与平均值之比为k，一般取值范围为20%～30%，电感值计算公式为

(30)

3 仿真分析

为验证文中所提方法的正确性，建立基于Matlab/Simulink的仿真模型．表1列出基于有功功率解的单相PWM整流系统的参数．

表1 单相PWM整流器系统参数

图11为系统在额定功率下，基于有功功率解耦的单相PWM整流器与传统变换器直流电压比较．传统变换器直流侧电容为660 μF，纹波电压50 V；新型变换器直流侧电容为330 μF，纹波电压约为4 V．显然，新型变换器能够有效滤除低频谐波电流，减小纹波电压，直流电压更加稳定．

图11 单相PWM整流器直流电压

图12和图13为负荷在50%～100%之间变换时，直流电压和交流侧电流波形．直流电压可在4个工频周期内达到稳定，响应速度快．交流侧电流变化平稳．

图12 负载功率变化时直流电压

图13 负载功率变化时交流侧电流

图14为交流侧输入电压和电流波形．从图中可知，电压电流同相位．单相PWM整流器为单位功率因数运行．

图14 交流侧电压和电流

图15和图16为直流侧电容电压交流分量和电感波形．且波形均为正弦波，与理论分析的结果一致．

图15 辅助支路电容电压交流分量

图16 辅助支路电感电流

4 结 论

基于有功功率解耦的单相PWM整流器具有响应速度快、输出功率稳定、纹波电压小等特点．它对2倍频谐波具有抑制作用，可减小主电路谐波电流，降低电磁干扰的影响，增强抗干扰能力．此外，与传统单相PWM整流器相比，新型变换器可选取小容量电容，有利于提高变换器能量密度，减小变换器体积．

[1] Musavi F, Eberle W, Dunford W G. A High-performance Single-phase Bridgeless Interleaved PFC Converter for Plug-in Hybrid Electric Vehicle Battery Chargers[J]． IEEE Trans. Ind. Appl., 2011,47(4)：1833-1843．

[2] Musavi F, Edington M, Eberle W. Evaluation and Efficiency Comparison of Front end AC-DC Plug-in Hybrid Charger Topologies[J]． IEEE Trans. Smart Grid, 2012,3(1)：413-421．

[3] Yilmaz M, Krein P T. Review of Battery Charger Topologies, Charging Power Levels, and Infrastructure for Plug-in Electric and Hybrid Vehicles[J]． IEEE Trans. Power. Electron., 2013, 28(5)：2151-2169．

[4] Chao K H, Cheng P T, Shimizu T. New Control Methods for Single Phase PWM Regenerative Rectifier with Power Decoupling Function[J]． In Proc. Power Electron. Drive Syst. Conf., Nov 2009：1091-1096．

[5] Fujita H. A Single-phase Active Filter Using an H-bridge PWM Converter with a Sampling Frequency Quadruple of the Switching Frequency[J]． IEEE Trans. Power Electron.,2009，24(4)．

[6] Thacker T, Wang R, Dong D. Phase-locked Loops Using State Variable Feedback for Single-phase Converter Systems[J]． Appl. Power Electron. Conf., 2009：864-870．

[7] Mao X, Ayyanar R, Krishnamurthy H K. Optimal Variable Switching Frequency Scheme for Reducing Switching Loss in Single-phase Inverters Based on Time Domain Ripple Analysis[J]． IEEE Trans. Power Electron., 2009, 24(4)：991-1000．

[8] Huber L, Jang Y, Jovanovic M M. Performance Evaluation of Bridgeless PFC Boost Rectifiers[J]． IEEE Trans. Power Electronics, 2008,23(3)：1381-1390．

[9] Wang R, Wang F, Boroyevich D. A High Power Density Single-Phase PWM Rectifier with Active Ripple Energy Storage[J]． IEEE Trans. Power Electronics., 2011, 26(5)：1430-1443．

[10] Li H, Zhang K, Zhao H, et al. Active Power Decoupling for High-Power Single-Phase PWM Rectifiers[J]． IEEE Trans. Power Electronics., 2013,28(3)：1308-1319．

[11] Hamid Rezaei, Hasan Rastegar, Mohammad Pichan. A New Active Power Decoupling Method for Single Phase PWM Rectifiers[J]． Iranian Conference on Electrical Engineering，2015， 23(3)：1665-1670．

[12] Krein P T, Balog R S. Cost-effective Hundred-year Life for Single-phase Inverters and Rectifier in Solar and LED Lighting Applications Based on Minimum Capacitance Requirements and a Ripple Power Port[J]． in Proc. IEEE Appl. Power Electron. Conf., Feb, 2009, pp.620-625．

[13] Yi Tang, Frede Blaabjerg, Poh Chiang Loh. Eoupling of Fluctuating Power in Single-Phase Systems Through a Symmetrical Half-Bridge Circuit[J]． IEEE Trans. Power Electronics., 2015，30(4)：1855-1865．

[责任编辑 张 莉]

Research on Active Power Decoupling of Single-phase PWM Rectifier with High Power Density

Wang Guixin Chen Haidong Tang Dayou Fang Xin Cheng Wei

(Hubei Provincial Collaborative Innovation Center for New Energy Microgrid, China Three Gorges Univ., Yichang 443002, China)

Single-phase PWM rectifier has second-order line frequency ripple power on DC-link， the output voltage will change with the load in period. The traditional way using passive filtering approach to filter low-frequency harmonic currents by adding high value capacitance to DC-link. The capacitance box has big size, which is disadvantage of designing high power density converter. This paper proposes an active power decoupling method to store ripple power in DC-link capacitance. This way can balance the output voltage and reduce the value of capacitance. And then this paper has studied the control strategy, which make the system with quick response and stabilize by voltage-current double-loop controller. Finally, the method is validated by simulation.

single-phase PWM rectifier; active power decoupling; ripple energy; double-loop control

10.13393/j.cnki.issn.1672-948X.2016.05.016

2016-04-08

王归新(1961-)，男，副教授，博士，研究方向为电力电子与电力传动．E-mail： 47424715@qq.com

TM461

A

1672-948X(2016)05-0080-07