水资源优化调度的改进量子遗传算法研究

王 攀 方国华 郭玉雪 闻 昕

(河海大学 水利水电学院， 南京 210098)



水资源优化调度的改进量子遗传算法研究

王 攀 方国华 郭玉雪 闻 昕

(河海大学 水利水电学院， 南京 210098)

针对于传统量子遗传算法在连续函数优化中出现的易陷于局部最优搜索、优化效率低等问题．本文通过深入研究量子遗传算法，将量子旋转门、量子全干扰交叉进行了改进，结合量子灾变操作，提出了一种改进的量子遗传算法，并运用于南水北调东线工程江苏段水资源优化调度研究．在50%、75%和95%三种保证率下，分别降低了系统缺水量的13.3%、13.9%、8.7%及总抽水量的13.6%、14.4%、11.1%，提高了水资源调度的合理性，取得了良好的效果．

量子遗传算法； 量子旋转门； 全干扰交叉； 量子灾变； 优化调度

水资源是人类社会生产、生活必不可少的物质基础，是极其重要的自然资源．随着社会的不断发展进步，人类对于水资源的需求急剧增长；同时由于天然降水分布不均、水资源保护措施缺乏及人类社会活动等的影响，直接或间接地产生了部分地区水资源短缺、分配不均等现象．因此，合理的水资源分配成为了全世界的关注热点，如何进行水资源优化调度成为了专家们的重要研究课题．

水资源优化调度是指采用系统分析方法和最优化技术，研究有关多水源配置系统管理运用的各个方面，并选择满足既定目标和约束条件的最佳调度策略的方法，其核心是通过水资源配置系统进行的水量调节，并具有多水源互济互调的特点．水资源系统的优化调度研究起步于20世纪50年代，由Hall及Dracup用于解决美国密苏里河流域6座水库的运行调度问题而设计．其后随着水资源系统分析理论的研究深入化，水资源系统模拟模型和联合优化调度的研究和应用工作发展迅速，涉及到的领域也越来越多．

近些年，学者们对于水资源优化调度的研究发展尤为突出．1982年，Beckor曾采用约束扰动法研究了水库群系统的多目标问题[1]；1990年，方淑秀等针对引滦调水工程五库供水系统的优化调度问题，采用聚集降维技术求得了该工程多级水库间的优化运行策略[2]；1999年，Robin和Mohd成功地将遗传算法应用于包含四座水库的水库群联合优化调度中，并对算法性能和优化潜力进行了相关分析[3]；2009年，方国华等提出了扰动遗传算法，提高了算法精确性，取得良好效果[4]；2011年，郭卫等提出人工鱼群遗传算法，应用于水库优化调度中，成果行之有效[5]；2014年，张忠波等将动态规划和改进遗传算法相融合，应用于水库调度[6]．学者们的研究为水资源优化调度的实际运用提供了极有价值的理论参考．

随着学者们的研究成果不断显现、数学规划理论的日益完善和计算机技术的广泛应用，水资源优化调度算法理论研究愈加成熟．从最早的线性规划技术[7-8]，到动态规划技术[9-11]、大系统分解协调技术[12-14]、多目标优化技术[15-16]的理论逐渐成熟．随着启发式智能优化算法(尤其是遗传算法)的提出并投入应用，水资源优化调度问题的研究手段和途径得到了极大的丰富．

目前，量子遗传算法(Quantum Genetic Algorithm，QGA)在遗传算法领域中发展迅速，备受重视．量子遗传算法是一种基于量子计算原理的概率优化的遗传算法[17-18]．QGA由Narayanan等[19]受量子计算思想启发，将量子多宇宙的概念引入遗传算法研究后提出．随后，Han等[20]引入了量子比特、量子旋转门的概念，在成功求解0-1背包问题后，掀起了全世界对于量子遗传算法的研究热潮，将QGA应用于各个领域．邵桂芳等[21]将量子遗传算法进行了改进，并应用于图像分割处理中，解决了传统分割算法的易丢失图像边缘信息、运算缓慢等问题；赵晓莉等[22]将实数编码混沌量子遗传算法应用于区域水资源可持续利用评价模型中参数的优化，取得了良好的效果．

众多学者对于QGA进行改进、优化，并应用于各个邻域，取得了一定的成果．但是，由于量子门旋转角度大小缺乏理论指导、量子交叉操作的随机性过大等因素的影响，改进的QGA依旧存在陷于局部最优搜索、优化效率较低、运行时间较长等诸多问题．本文通过对量子遗传算法的研究，提出了一种新的改进型(Improved Quantum Genetic Algorithm，IQGA)，并将其应用于水资源优化调度研究中，取得了良好的优化效果，给实际操作提供了理论支持．

1 改进量子遗传算法

量子遗传算法将量子力学中的量子比特、量子态叠加等概念运用于遗传算法中，通过将量子旋转门作用于染色体基因的更新调整，完成进化操作．但是对于相对复杂的工程问题，QGA存在一定的缺陷：(1)容易陷入局部最优解，无法保证对于全局的寻优；(2)优化效率低，无法快速进行全局寻优．

由此本文通过对量子旋转门的改进、加入量子交叉并对其改进、加入量子灾变操作等方式，对传统的量子遗传算法进行了改进，提出了一种改进量子遗传算法(improved quantum genetic algorithm，IQGA)．

1.1 量子比特编码

在IQGA中，染色体的表示不使用确定性的值(例如实数、二进制数、浮点数或符号等)，而是用量子比特(quantum bit，qubit)表示，它是一种随机概率的表示方式．一个量子比特的状态主要分为基态、叠加态，即量子比特不仅可以表示|1〉或|0〉两种基态，还可表示这两种状态之间的任意中间态，即叠加态|Ψ〉．

因此，一个量子位的状态可表示为

(1)

式中，α和β可以是复数，表示相应状态的概率幅，且满足下列归一化条件：

(2)

式中，|α|2表示|Ψ〉坍塌到|0〉的概率，|β|2表示|Ψ〉坍塌到|1〉的概率．

由此，IQGA算法中的染色体可用下式方式进行定义：

(3)

式中，k=1，2，…，g；g表示种群大小；m表示染色体长度；t表示第t代子代种群．

1.2 量子旋转门操作及其改进

在QGA中，种群更新和染色体的交叉是最关键的进化方式．在种群更新中，由于染色体的状态处于叠加或纠缠状态，故采用量子门完成更新操作．量子门作用于量子叠加态或纠缠态的基态，使其相互干涉，产生相位变化，改变其概率幅值，因此直接关系到QGA的最终性能．在QGA中，主要采用的量子旋转门(Qgate)及其操作方式如下式：

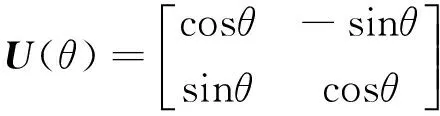
(4)

(5)

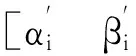
但是现如今对于旋转角度大小Δθ的理论指导较为缺乏，只有一个在[0.001π，0.05π]区间的固定值，存在明显的局限性：当Δθ过小，将影响算法的收敛速度；当Δθ过大，则容易导致算法的早熟，不利于全局解搜索．同时在传统的量子旋转门操作中，基因位的值可趋近于0或1，容易使得算法陷入局部最优解，从而使算法过早收敛．故本文通过改进旋转角度Δθ、修正概率幅值两方面对传统量子旋转门进行改进，以加强算法的全局寻优性能．

1)改进的旋转角度Δθ，表达式为：

(6)

(7)

式中，θmin为Δθ的固定值的最小值，取0.001π；θmax为Δθ的固定值的最大值，取0.05π；K为调整系数；fmax和fx分别指搜索到的最优个体适应度和当前个体的适应度值；gen表示当前的代数；MAXGEN表示最大迭代次数．

由上述改进可知：当当前个体适应度值较低时，Δθ越大，加快整体搜索速度；当当前个体适应度较大时，Δθ越小，进行局部搜索，有利于搜寻到最优解；

2)概率幅值修正[23]，具体操作如下：

①若|αi|2≥1-ϖ，且|βi|2≤ϖ

(8)

②若|αi|2≤ϖ，且|βi|2≥1-ϖ

(9)

③若|αi|2≥ϖ，且|βi|2≤1-ϖ

(10)

式中，ϖ∈(0，1)．当ϖ取值过大，将影响算法的收敛，本文取为0.01．

1.3 量子交叉操作及其改进

量子交叉的主要作用即是增加种群的多样性，防止未成熟收敛，QGA通常采用全干扰交叉操作[24](对角线排列组合方式)，如图1所示．

图1 对角线排列组合方式的全干扰交叉操作

以种群规模为5，量染色体长度为7的交叉操作为例．经典量子交叉后得到S1′：A(1)→B(2)→C(3)→D(4)→E(5)→A(6)→B(7)，同理可得到S2′、S3′、S4′、S5′，由此交叉操作完成．

这类交叉操作相比于单点交叉，有着明显的优势，但也有其局限性：虽然能够很好维持种群多样性，但是随机性偏大，有一定的盲目性，产生的新解可能不具有竞争性，并有丢失优良个体的可能性．

本文通过对上述缺陷的分析，在IQGA中对其进行了下述改进：在量子全干扰交叉操作中加入最优保留机制，记录当前最优个体，在完成量子全干扰交叉操作后，将当前最优个体取代其中一个交叉操作完成后的个体，由此避免优良个体的丢失．

1.4 量子灾变操作

为了避免传统量子遗传算法陷入局部最优解，本文在IQGA中使用群体灾变策略避免算法陷入局部寻优．群体灾变策略如下：当算法连续多代(本文取10代)的最优个体都不发生任何变化时(认为已陷入局部最优解)，则在保留最优个体的同时，对其余个体全部重生成．由此可使算法有效摆脱局部寻优，从而得到全局最优解．

1.5 算法流程

综上所述，本文提出的改进量子遗传算法的运算步骤如下：

2)根据Q中各个体的概率幅构造出量子叠加态的观测态K，K={a1，a2，…，an}，其中an(j=1，2，…，n)为每个个体的观测状态，即一个长度为n的二进制串．在IQGA中，由概率幅Q构造观测态K的过程包含解码过程，解码后得到各优化参数的当前实际值；

3)对观测态进行适应度评估；

4)保留观测态K中适应度最佳的个体，并判断是否满足终止条件，满足，则算法终止，否则，执行下一步；

5)根据本文的量子旋转角的调整策略计算旋转角Δθ，并用H门对量子旋转门操作后的概率幅进行修正，即更新Q；

6)进行量子交叉操作；

7)判断是否需要进行量子灾变，如果满足，则进行量子灾变操作；如果不满足，则进行步骤8)；

8)进化代数增1，返回步骤2)继续执行，直到算法结束．

本文提出的改进量子遗传算法流程如图2所示．

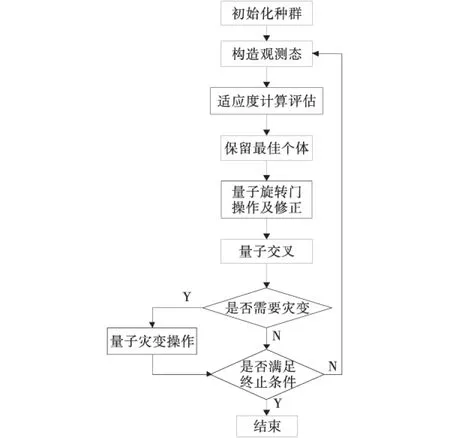
图2 改进量子遗传算法流程图

1.6 算法性能测试

为验证算法的有效性及其可行性，本文使用简单平方和函数、二维多峰函数、DeJong函数、Schaffer函数等4个复杂函数对算法进行测试，并与遗传算法、经典量子遗传算法进行比较分析．

1)简单平方和函数：

该函数只有一个极小值点：f1(xi=0)=0，i=1，2．

2)二维多峰函数：

f2(x)=e-0.001xcos2(0.8x)，0≤x≤12

该函数在其定义域内有且仅有一个全局最大值f2(0)=1；另有3个峰值，分别为f2(3.926 2)=0.996 1；f2(7.853 2)=0.992 2；f2(11.781 0)=0.988 3．

3)DeJong函数：

-2.048≤x，y≤2.048

该函数具有一个全局最小值：f4(1，1)=0；且该函数为病态函数，难以进行全局解的搜索．

4)Schaffer函数：

-100≤x，y≤100

该函数具有唯一的全局最小点：f5(0，0)=0．

每个测试函数分别用遗传算法、传统量子遗传算法、改进型量子遗传算法运行100次．其中的参数如下：种群大小均为30，染色体长度均为20，交叉概率均为0.95，变异概率均为0.05，进化代数为300．算法的优化性能从算法的效率及其质量两方面进行评估．前者主要由算法收敛成功率、最佳值、平均值3项指标来判断；后者主要由平均计算时间来进行评价．计算结果及对比见表1．

表1 GA、QGA、IQGA性能测试成果表

由表1可知：4个函数的IQGA计算结果的平均值相较于GA、QGA更接近于理论最优解；f2、f3两个函数用GA计算时，成功率很低(分别为22%、40%)，QGA算法成功率高于GA(分别为98%、90%)，用IQGA计算时，则都能取得100%的成功率；说明IQGA相对于QGA、GA具有更好的全局收敛性，有着更强的搜索性能；由于本身算法的复杂性，导致IQGA相比较于GA、QGA计算的时间更长．综上所述，IQGA相较于GA与QGA在计算的准确性及稳定性方面的优势非常明显，即本文提出的IQGA算法能有效避免局部最优解，达到全局寻优的效果，提高了优化的效率．

2 实例应用分析

2.1 南水北调东线工程江苏段水资源优化调度模型建立

为使工程能够发挥期望效益、实现高效运行，本文甄别选取了缺水量与泵站抽水量两个优化目标，根据系统构成与特点考虑了湖泊水量平衡约束、泵站工作能力约束、控制闸站最大过流能力约束、湖泊北调控制水位约束等几种约束条件，构成了南水北调东线工程江苏段水资源优化调度模型．

2.1.1 工程概况

南水北调东线工程江苏段在原江苏省江水北调工程的基础上扩大规模、向北延伸而成，其受水区地处淮河及沂沭泗流域下游，位于北纬32°15′～34°30′，东经117°00′～119°45′，涉及扬州、淮安、盐城、宿迁、连云港和徐州六市，耕地约2 930万亩，从长江下游取水，供给江苏、山东、安徽三省20个地级市共69个县(区)，直接受益人口约1亿人．输水干线全长1 467 km，河道共计17条．黄河以南沿线串联有洪泽湖、骆马湖、南四湖下级湖3个调蓄湖泊，调蓄湖泊总库容达45.25亿m3，各调蓄湖泊主要特征参数见表2．若以湖泊为节点，则从长江至南四湖下级湖共可分为3个大段，每段设3级提水泵站，共计9个提水梯级(现已建成22座泵站，总装机容量17.6万kW)．

表2 南水北调东线一期工程江苏段主要调蓄湖泊特性参数表

注：洪泽湖骆马湖采用废黄河高程，下级湖采用85国家高程

本文根据工程沿线各部门用水户的主要取水位置将供水范围重新划分为了7个计算分区，江苏省以北(南四湖的下级湖以北地区)为一个计算分区，江苏省内共划分了6个，分别为：江淮区间、洪泽湖区间、洪骆区间、骆马湖区间、骆微区间和下级湖区间．各个分区的概化示意图如图3所示．

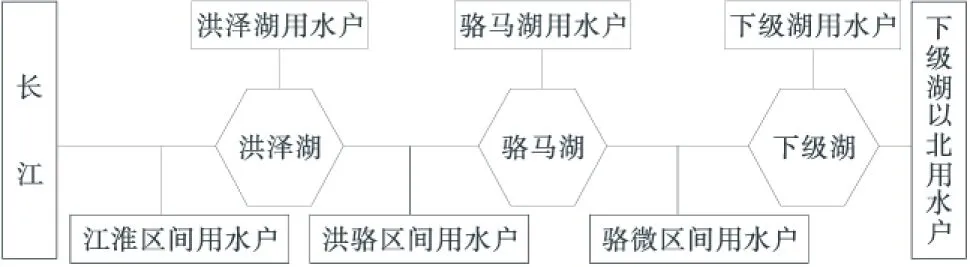
图3 南水北调东线工程江苏段受水区用水户概化示意图

2.1.2 目标函数

本文采用权重系数将缺水量、泵站抽水量两个优化目标转化单目标进行计算，目标函数的数学公式表达如下：

(11)

式中，t为时段序号；T为一年的旬数，取为36；i为分区编号；n为分区个数，取为7；QR(i，t)为t时段i分区的缺水量(亿m3)；QS(i，t)为t时段i分区的系统抽水量(亿m3)；α表示权重系数，表示缺水量与系统总抽水量的相对重要性比重[25]，本文取0.75．

2.1.3 约束条件

1)湖泊水量平衡约束

根据图2的概化图，每一个湖泊都可以各自组成一个单元，而每一个单元在每一个时段都必须要满足水量平衡约束．具体各单元通过图4的“一湖一河网”子系统方式运行，并满足如下水量平衡方程式：

(12)

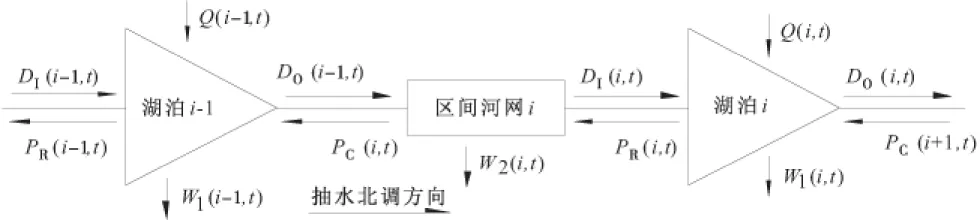
图4 “一湖一河网”水量交换子系统示意图

图中，i为湖泊编号(1-洪泽湖、2-骆马湖、3-下级湖)；t为时段数；Q(i，t)表示i湖泊t时段的入湖径流量；W1(i，t)、W2(i，t)分别表示t时段i湖泊和i河网的需水量，为扣除当地可用水量后需由南水北调工程补充的水量．DO(i，t)、DO(i-1，t)分别表示t时段i湖泊和i-1湖泊的抽湖北调水量；DI(i，t)、DI(i-1，t)表示i湖泊和i-1湖泊t时段的抽水入湖水量；PC(i，t)、PC(i+1，t)表示t时段下泄进入i-1湖泊和i湖泊的水量，PR(i，t)、PR(i-1，t)表示t时段由i湖泊和i-1湖泊自流下泄的水量．

2)泵站工作能力约束

北调抽水水量应不大于相应泵站最大工作能力：

(13)

式中，DOmax(i，t)、DImax(i，t)分别表示相应泵站的最大抽水能力．

3)控制闸站最大过流能力约束

湖泊下泄水量应不大于相应控制闸站最大过流能力：

(14)

式中，PRmax(i，t)为相应控制闸站的最大过流能力．

4)湖泊调蓄能力约束

(15)

式中，Vmin(i，t)、Vmax(i，t)分别表示相应湖泊t时段的最小蓄水能力(死库容)和最大蓄水能力(蓄满库容)．

5)北调控制水位约束

为了使当地的用水利益不致因北调抽水而受到损害，在实际的试行调度方案中还规定了湖泊不同时段的北调控制水位．一般情况下，当湖泊水位低于此水位时，停止抽湖泊既有蓄水北调．调蓄湖泊北调控制水位表见表3．

表3 调蓄湖泊北调控制水位表(单位：m)

注：下级湖为1985国家高程基准；洪泽湖、骆马湖为废黄河高程．

6)其余约束

河道输水能力约束、非负约束(流量非负等)．

2.2 南水北调东线工程江苏段水资源优化调度模型求解及分析

本文选取2020年为规划水平年，通过采用P-Ⅲ型曲线进行水文频率计算；受水区汛期为6月至9月，将模型计算起始时间设为汛期开始；选择汛限水位作为各个湖泊的起调水位．基于改进型量子遗传算法的模型求解计算参数设置为：种群大小均为100，染色体长度均为20，交叉概率均为0.95，变异概率均为0.05，进化代数为1500．计算分别按照50%(平水年)、75%(枯水年)和95%(特枯水年)保证率进行，取得较好的收敛效果，结果收敛曲线如图5～7所示，将优化调度与常规调度[26]结果进行了对比分析，详见表4、图8．

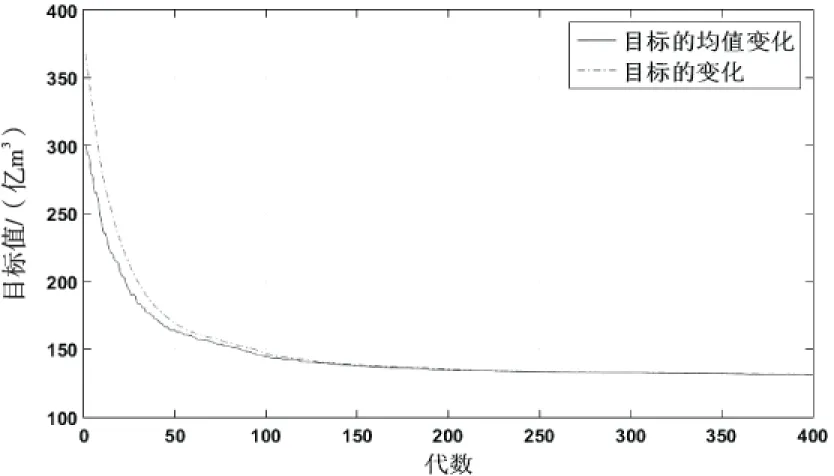
图5 50%保证率下系统适应度值-迭代次数曲线

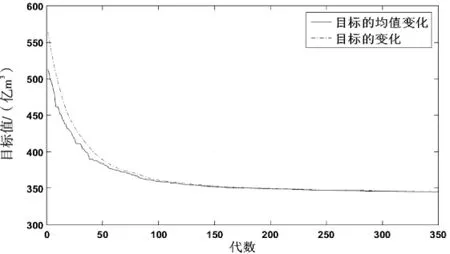
图6 75%保证率下系统适应度值-迭代次数曲线

图7 95%保证率下系统适应度值-迭代次数曲线

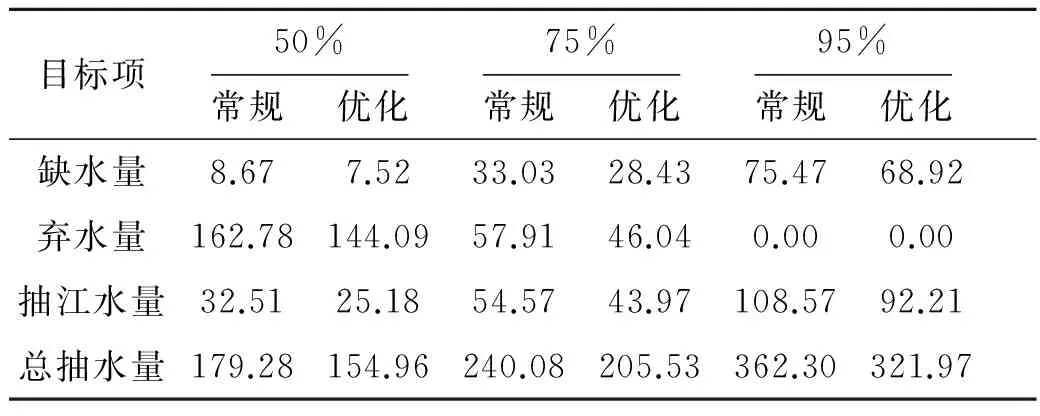
目标项50%常规 优化75%常规 优化95%常规 优化缺水量8.677.5233.0328.4375.4768.92弃水量162.78144.0957.9146.040.000.00抽江水量32.5125.1854.5743.97108.5792.21总抽水量179.28154.96240.08205.53362.30321.97

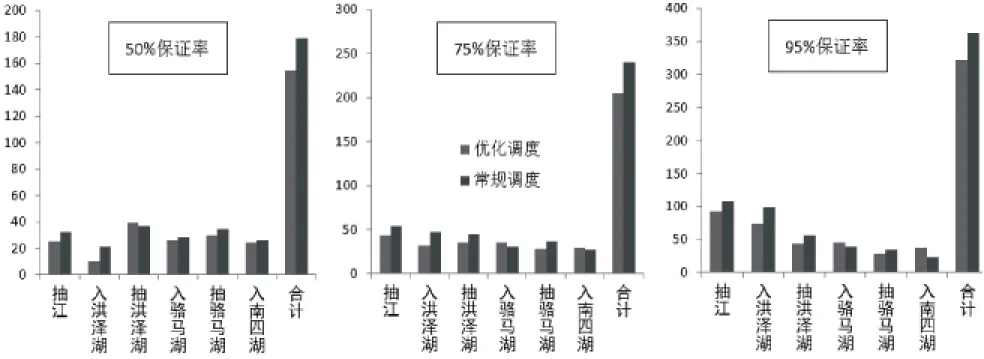
图8 各保证率下两种调度方式分区出入水量结果对比图

通过以上结果对比可以发现：

1)采用优化调度方式能有效提高系统的供水能力，减少用户缺水．根据上述对比数据，在50%、75%和95%三种保证率下，采用优化调度方式产生的系统缺水均小于常规调度方式，说明面对不同的工况背景，优化调度模型均能通过合理调度提供更多供水，体现了较为稳健的优化能力．具体而言，优化调度的系统缺水量在50%、75%、95%保证率下分别比常规调度降低了1.15亿m3(13.3%)、4.60亿m3(13.9%)和6.55亿m3(8.7%)，说明在优化调度模型能很好发挥“减少系统缺水”这一优化作用．

2)采用优化调度方式能显著减少各级泵站的总抽水水量，降低系统的运行成本．对比数据显示，在50%、75%和95%三种保证率下，采用优化调度模型计算出的总抽水量分别比常规调度减少了24.32亿m3(13.6%)、34.55亿m3(14.4%)和40.33亿m3(11.1%)，体现了良好的优化效果．

3)采用优化调度方式能提高系统内水资源的利用效率．根据对比数据，在50%、75%、95%保证率下，采用优化调度模型计算得出的总弃水量分别比常规调度减少18.70亿m3(11.5%)、11.86亿m3(20.5%)和0.00亿m3(无弃水)．常规调度方式下的弃水更多说明该模式下湖泊的调蓄功能并没有被充分发挥，对天然来水的利用效率不高．

3 结 语

本文提出了一种改进的量子遗传算法，与遗传算法、传统的量子遗传算法进行了对比分析，取得了较好的全局寻优的效果．但是在算法的运行速度上还有待进一步研究，本文运算大约需350～450代左右收敛，可进一步减少算法的迭代次数，减少其运行时间．

同时，虽然本文将改进的遗传算法应用于水资源优化调度的模型求解研究中，取得了良好的效果，给南水北调东线工程江苏段的水资源调度实际应用提供了理论指导．但是在工程系统概化上与实际情况有部分出入点，实际情况的系统概化更为详细，如何更切合实际地进行系统概化分析，还有待进一步研究．

[1] Bechor G L. Multi-objective Analysis of Multi-reservoir Operations[J]． Water Resources Research， 1982，18(5)：1326-1336．

[2] 方淑秀，黄守信，王孟华，等.跨流域引水工程多水库联合供水优化调度[J]．水利学报，1990，(12)：1-8．

[3] RobinW，Mohd S. Evaluation of Genetic Algorithms for Optimal Reservoir System Operation[J]． Journal of Water Resources Planning and Management，1999，125(1)：25-33．

[4] 方国华，耿建强.水库优化调度扰动遗传算法研究[J]．水电能源科学，2009(6)：38-40．

[5] 郭 卫，方国华，黄显峰.基于人工鱼群遗传算法的梯级水库优化调度研究[J]．水电能源科学，2011(6)：49-51．

[6] 张忠波，吴雪春，张双虎，等.并行动态规划和改进遗传算法在水库调度中的应用[J]．水力发电学报，2014(4)：21-27．

[7] Hall W A，Shephard R W.Optimum Operation for Planning of a Complex Water Resources System[C]．Technology RepWater Resources Cent School of Engineering and Applied Science． San FranciscoUniversity of California，1967．

[8] 都金康， 李罕， 王腊春，等. 防洪水库(群)洪水优化调度的线性规划方法[J]．南京大学学报：自然科学版，1995，31(2)：301-309．

[9] Turgeon A. Optimal Short-term Hydro Scheduling from the Principle of Progressive Optimality[J]． Water Resources Research， 1981，17(3)：481-486．

[10] 王丽萍，孙平，蒋志强，等.并行多维动态规划算法在梯级水库优化调度中的应用[J]．水电能源科学，2015(4)：43-47，80．

[11] Jamshidi M. Large Scale System： Modeling and Control， Northholland[M]． New York： Elsevier Science Ltd， 1984：30-36．

[12] 谢新民， 周之豪. 水电站水库群与地下水资源系统联合运行多目标管理模型[J]． 水电能源科学， 1993，11(2)：96-104．

[13] Bechor G L. Multi-objective Analysis of Multi-reservoir Operations[J]． Water Resources Research， 1982，18(5)：1326-1336．

[14] Mohan S， Raipure D M. Multi-objective Analysis of Multi-reservoir Operations[J]． Water Resources Plan Mgmt， 1992，9(5)：356-370．

[15] 廖伯书，张勇传.水库优化运行的随机多目标动态规划模型[J]．水利学报，1989(12)：43-49．

[16] 杨 侃， 刘云波. 基于多目标分析的库群系统分解协调宏观决策方法研究[J]． 水科学进展， 2001，11(2)：232-236．

[17] 王 凌.智能优化算法及其应用[M]．北京：清华大学出版社，2001．

[18] Yang J A， Li B， Zhuang Z Q，et al. Quantum Genetic Algorithm and Its Application Research in Blind Source Seperation[J]．Mini-micro Systems，2003，24(8)：1518-1523．

[19] Narayanan A， Moore M. Quantum-inspired Genetic Algorithms[C]． Procof IEEE International Conference on Evolutionary Computation. Nagoya， Japan： IEEE Press， 1996．

[20] Han K H， Kim J H. Genetic Quantum Algorithm and Its Application to Combinatorial Optimization Problem[A]． IEEE IntConf on Evolutionary Computation[C]． LaJolla，2000：1354-1360．

[21] 邵桂芳，李祖枢，刘 恒，等.基于遗传量子的自适应图像分割算法[J]．计算机工程，2005，31(22)：189-191．

[22] 赵晓莉，李祚泳，丁 晶.改进型量子遗传算法应用于区域水资源可持续利用评价[J]． 自然资源学报，2007(6)：980-985．

[23] 张小锋，睢贵芳，郑 冉，等.一种改进的量子旋转门量子遗传算法[J]． 计算机工程，2013，39：234-238．

[24] 焦李成，杜海峰，刘 芳，等.免疫优化计算、学习与识别[M]．北京：科学出版社，2006：184-190．

[25] 张建云，陈洁云.南水北调东线工程优化调度研究[J]．水科学进展，1995(3)：198-204．

[26] 王文杰，吴学文，方国华，等.南水北调东线工程江苏段水量优化调度研究[J]．南水北调与水利科技，2015，13：7803：422-426．

[责任编辑 王迎春]

Research on Water Resources Optimal Scheduling Based on Improved Quantum Genetic Algorithm

Wang Pan Fang Guohua Guo Yuxue Wen Xin

(College of Water Conservancy and Hydropower Engineering, Hohai Univ., Nanjing 210098, China)

In view of the problems such as easy to fall into the local optimal search, low efficiency of traditional quantum genetic algorithm in continuous function optimization. In order to address the issue, this paper proposes an improved quantum genetic algorithm by making an intensive study of quantum genetic algorithm, improving quantum rotation gate and full quantum interference, and combining quantum catastrophe operation, used in the studies of optimal scheduling of water resources in Jiangsu Section of South-to-North Water Transfer Eastern Route Project, the amount of water shortage about13.3%, 13.9%, 8.7% and total pumping capacity about 13.6%, 14.4%, 11.1%, at three kinds of guaranteed rates of 50%, 75%, 95%, so as to significantly improve the rationality of water resources scheduling and achieve good results.

quantum genetic algorithm; quantum rotation gate; full interference crossover; quantum catastrophe; optimal scheduling

10.13393/j.cnki.issn.1672-948X.2016.05.002

2016-06-30

长江科学院开放研究基金资助项目(CKWV2016370/KY)；中央高校基本科研业务费用专项资金资助(2015B28614)；江苏高校优势学科建设工程资助项目；江苏省水利科技项目(2014012)

方国华(1964-)，女，教授，博士生导师，主要从事水利经济与水利规划方面的研究．E-mail：382445615@qq.com

TV213

A

1672-948X(2016)05-0007-07