基于马尔科夫键蒙特卡洛抽样的最大似然时差-频差联合估计算法
赵拥军 赵勇胜 赵 闯
基于马尔科夫键蒙特卡洛抽样的最大似然时差-频差联合估计算法
赵拥军*赵勇胜 赵 闯
(解放军信息工程大学导航与空天目标工程学院 郑州 450001)
该文针对无源定位中参考信号真实值未知的时差-频差联合估计问题,构建了一种新的时差-频差最大似然估计模型,并采用马尔科夫链蒙特卡洛(MCMC)方法求解似然函数的全局极大值,得到时差-频差联合估计。算法通过生成时差-频差样本,并统计样本均值得到估计值,克服了传统互模糊函数(CAF)算法只能得到时域和频域采样间隔整数倍估计值的问题,且不存在期望最大化(EM)等迭代算法的初值依赖和收敛问题。推导了时差-频差联合估计的克拉美罗界,并通过仿真实验表明,算法在不同信噪比条件下的估计精度优于CAF算法和EM算法,且计算复杂度较低。
无源定位;时差;频差;联合估计;最大似然;马尔科夫链蒙特卡洛方法
1 引言
无源定位是近年来备受关注的问题,在雷达[1]、声呐[2]、无线通信[3]、传感器网络[4]等领域应用广泛。而时差(Time Difference Of Arrival, TDOA)和频差(Frequency Difference Of Arrival, FDOA)作为无源定位所需的基本参数[5],其估计精度将直接决定对目标的定位精度。因此,研究高精度的时差-频差估计算法具有重要意义。
互模糊函数(Cross Ambiguity Function, CAF)方法是处理时差-频差联合估计的经典算法[6],本质是时差-频差的2维相关。在高信噪比和高采样率条件下,互模糊函数方法可以得到时差-频差的精确估计,但其需要在参数空间上进行网格搜索求解,效率较低,且只能得到时域和频域采样间隔整数倍的时差-频差估计值。为此,一些针对互模糊函数计算的快速算法被提出,如基于快速傅里叶变换,分数阶傅里叶变换,两步估计等的改进算法。这些算法一定程度上减小互模糊函数的计算量。此外,基于高阶累积量[11],小波变换[12],以及自适应算法也被提出,在一些特定情况得到了优于传统CAF算法的估计效果。但本质上,这些改进算法仍然是时差-频差的2维相关,其估计精度仍受到时域和频域采样间隔的限制。为此,文献[13]提出了基于期望最大化(Expection Maximum, EM)的时差-频差估计算法。EM算法不受采样间隔的限制,但由于其求解过程中需多次对矩阵求逆,计算量过大,限制了信号的实时处理,且作为一种迭代算法,EM算法存在初值依赖和局部收敛问题。
马尔科夫链蒙特卡洛方法(Markov Chain Monte Carlo, MCMC)方法作为一种重要的Monte Carlo方法,是以概率统计理论为指导的,用随机数抽样来解决参数估计问题的一类数值计算方法,因其较高的灵活性,以及在复杂高维、高度非线性等问题中表现出的优异性能[14],近年来在参数估计领域中得到了广泛的应用。文献[15]利用MCMC方法估计降水-径流模型中的未知参数;文献[16]采用MCMC方法实现合成孔径雷达中运动目标的线性调频(chirp)回波信号的参数估计。文献[17]针对阵列信号测角问题,通过引入可逆跳转马尔科夫链蒙特卡罗(Reversible Jump Markov Chain Monte Carlo, RJMCMC)方法实现了真正意义上的信号源数和到达角度的联合估计。文献[18]将MCMC方法应用到时延估计问题中,得到了优于传统算法的估计性能。这类算法的思想是建立待估参数的概率模型或随机过程,然后利用MCMC方法对概率模型或随机过程抽样,通过对样本的统计实现参数的估计,具有估计精度高、计算复杂度低的优点。
本文针对无源定位中参考信号真实值未知的时差-频差联合估计问题,构建了一种新的时差-频差最大似然估计模型,并采用MCMC方法求解似然函数的全局极大值,得到时差-频差估计。MCMC方法通过生成时差-频差样本,并对样本进行统计得到估计值,可以突破传统算法只能得到采样间隔整数倍的限制,具有较高的估计精度,且计算复杂度较低。
2 信号模型和似然函数
考虑如图1所示的无源双基地雷达系统。参考天线用于接收来自外辐射源的直达信号,监视天线用于接收目标回波信号[1]。

图1 无源双基地雷达系统配置






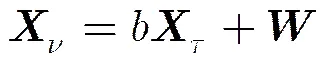



对式(10)中的概率密度函数取对数并去掉常数项,得到对数似然函数为
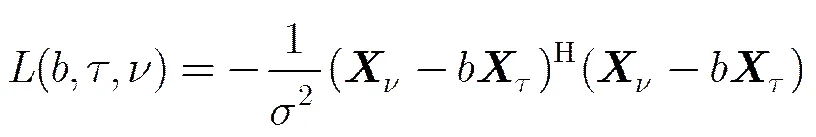



3 时差-频差联合估计
文献[19]提出的处理非线性问题全局最优解的基本理论为寻找一种无需搜索且不存在初值依赖的全局最优算法奠定了基础。根据文献[19]的理论,使得对数似然函数取得全局最大值的变量可以通过式(15)得到

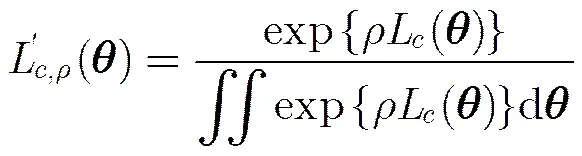
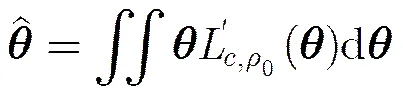
式(17)中的积分难以直接通过解析方法计算。但是如果能够得到足够多服从分布的样本,则可以通过数值计算方法估计式(17)中的积分。假设已经得到了个的样本,那么式(17)中积分可通过统计样本均值近似得到。
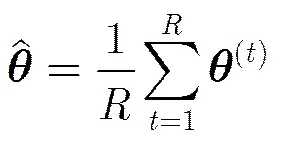
3.1 MCMC方法
MCMC方法的第1个“MC”, Markov Chain,表示利用Markov Chain从目标分布中抽取样本,第2个“MC”, Monte Carlo,则表示在抽取的样本下利用Monte Carlo方法对积分进行计算。它的基本思想是通过建立一个平稳分布为的马尔可夫链来得到服从分布的样本,然后通过对样本的统计来估计参数值。对于本文最大似然估计模型,平稳分布即为的后验分布。
Metropolis-Hasting(M-H)抽样是构造马尔科夫链的常用方法。MCMC方法的精髓在于构造合适的马尔科夫链,因此算法的主要目的是对马尔科夫链,在给定一个所处状态下,产生下一步的状态。M-H算法构造马尔科夫链的主要步骤总结如下:
(3)重复(直至马氏链达到平稳状态):

为此,本文采用自适应的随机游走采样方法,自适应地控制增量方差的大小,使其随着抽样次数的增加取值不断减小,即游走的范围不断缩小。在抽取第个样本时,

3.2 基于MCMC的时差-频差估计
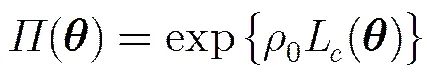
同时为避免式中指数运算的数值过大,令

那么最终构建马尔科夫链的平稳分布函数为

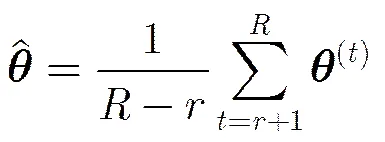

图2 对平稳分布函数形状的影响
综上,利用MCMC方法进行时差-频差联合估计的具体实现过程总结如下:
4 CRLB分析




式中,
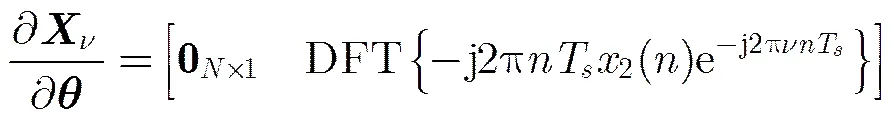

那么,Fisher信息矩阵为

CRLB是无偏算法估计误差的理论下限,其等于Fisher信息矩阵的逆。那么时差和频差的估计误差方差满足式(32)中的不等式

5 仿真实验
选取一段BPSK信号作为辐射源信号,进行仿真实验。BPSK信号参数设置为:码元速率,信号载频。采样频率,信号快拍数,两路信号之间的时差,频差。信号的信噪比初步设置为10 dB, MCMC方法的参数初步设置为,,,。
图3给出了信号信噪比为10 dB时利用MCMC方法抽取的时差频差样本。可以看出,抽样过程开始后,样本很快收敛至平稳分布,然后围绕着时差频差真实值上下波动。统计不同样本数量下MCMC算法估计的均方根误差(Root Mean Square Error, RMSE),结果如图4所示。可以看出,随着样本数量的增加,时差和频差的估计精度均不断提高,但提高的速度变慢,在样本数量增加至2000后,基本不再提高。且样本数量的增加意味着计算复杂度的增加,因此,作为折中,在后续仿真中样本数量设置为。

图3 MCMC方法抽取样本图 图4 不同样本数量下算法的RMSE
为评估算法估计性能,在不同信噪比条件下利用算法进行蒙特卡罗仿真。算法的估计误差为1000次仿真的RMSE。为了突出本文基于MCMC的ML(MCMC-ML)算法性能,将算法的RMSE与基于FFT的CAF(FFT-CAF)算法[10]、EM算法[13]和CRLB对比。仿真结果如图8所示。
从图8(a)可以看出,随着信噪比的增加,几种算法的时差估计精度均有提高。但FFT-CAF算法在信噪比增加至5 dB后,估计精度基本保持不变,不再随信噪比的增加而提高。原因在于FFT-CAF只能得到时域和频域采样间隔整数倍的时差-频差估计,估计精度受到限制。EM算法和MCMC-ML算法均可得到频域和时域采样间隔非整数倍的时差-频差估计,因此在-5 dB至20 dB信噪比范围内,估计精度可随着信噪比的增加而不断提高,但EM算法的估计精度对初值依赖严重。初值较差时,EM算法的估计精度低于CAF算法。而在给定较为准确的初值时,EM算法的估计精度高于CAF算法,较高信噪比条件下估计精度与MCMC-ML算法相近,但在信噪比较低时的估计精度低于本文MCMC-ML算法。图8(b)表明,MCMC-ML算法在频差估计中性能同样优于FFT-CAF算法和EM算法,但与时差估计相比不同的是,几种算法对频差估计的精度均相对较高,这主要由信号的互模糊特性决定。
算法的计算复杂度也是衡量算法优劣的重要指标。为此,这里比较本文MCMC-ML算法,基于网格搜索的ML(Grid search-ML)算法,FFT-CAF算法及EM算法的计算复杂度。由于实际运算过程中运算量主要由复数乘法运算次数决定,因此将算法复数乘法的次数作为衡量算法计算复杂度的指标。为便于统计,这里将共轭运算和指数运算均作为一次复数乘法运算参与统计。结果如表1所示。其中,分别为Grid search-ML算法和FFT-CAF算法在时差和频差取值区间划分点数。为MCMC算法的样本数。为EM算法的迭代次数。

图5 对算法性能的影响 图6 对算法性能的影响 图7 对算法性能的影响
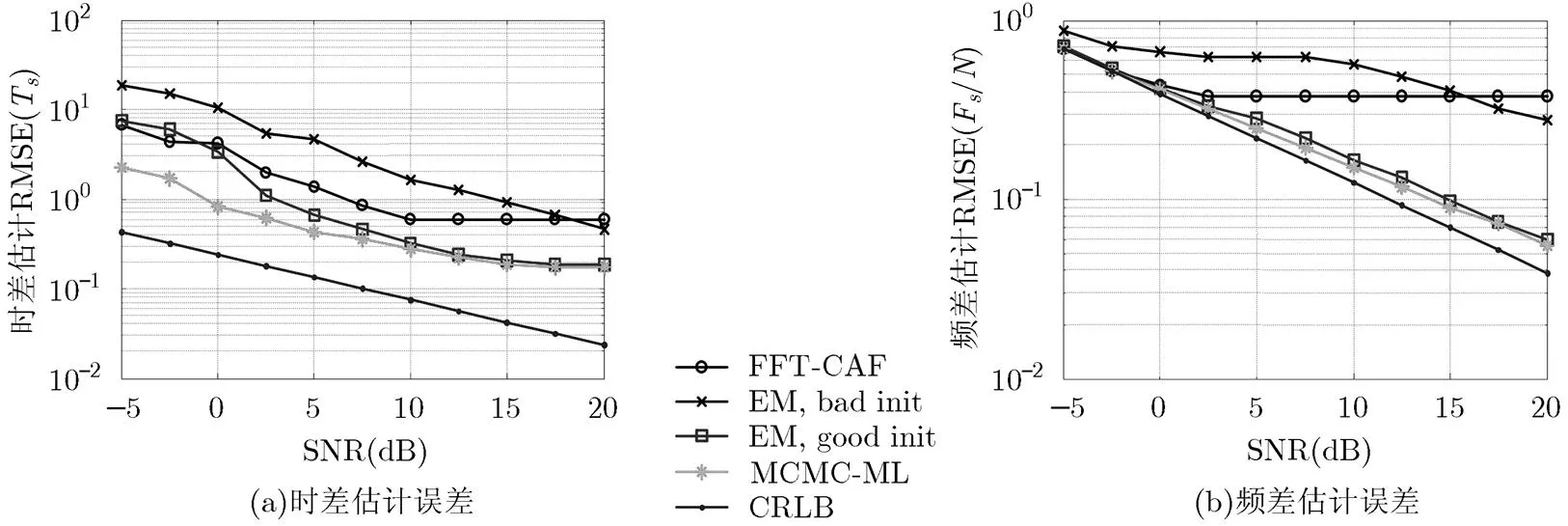
图8 不同信噪比条件下算法的估计误差
从表1可以看出,4种算法中,Grid search-ML算法的计算计算复杂度最高,难以满足实时处理的要求。而与之相比,MCMC-ML算法的计算复杂度很低,与FFT-CAF算法的计算复杂度相当。EM算法计算复杂度较高,原因在于EM算法在期望最大化的迭代过程中需多次对的矩阵求逆,造成算法计算复杂度的急剧增加。从计算复杂度的表达式可以看出,本文MCMC-ML算法的计算复杂度主要由信号快拍数和样本数量决定,计算复杂度随着生成样本数的增加而增加。对于仿真BPSK信号情况,MCMC-ML算法的计算复杂度低于FFT-CAF快速计算方法,可以满足信号实时处理的要求。
6 结论
针对无源双基地定位中参考信号真实值未知的时差-频差联合估计问题,本文构建了一种新的时
差-频差最大似然估计模型,并采用MCMC方法求解最大似然模型,得到时差-频差估计。MCMC方法通过生成时差-频差的样本,进而通过统计样本均值得到时差-频差估计。算法的计算复杂度与利用FFT的CAF快速计算方法基本相同,但是克服了CAF算法只能得到时域和频域采样间隔整数倍的时差-频差估计问题,可以得到采样间隔非整数倍的时差-频差估计,因此估计精度高于CAF算法。而与EM算法相比,本文算法不存在迭代的初值依赖和收敛问题,且计算复杂度远低于EM算法。推导了时差-频差联合估计的CRLB,并通过仿真实验表明,算法的估计精度优于CAF算法和EM算法。
表1不同算法的计算复杂度对比

算法计算复杂度BPSK信号计算复杂度比 MCMC-ML 1.000 Grid search-ML 2095.900 FFT-CAF 1.102 EM 808.070
[1] HIGGINS T, WEBSTER T, and MOKOLE E L. Passive multistatic radar experiment using WiMAX signals of opportunity. Part 1: Signal processing[J].,&, 2016, 10(2): 238-247. doi: 10.1049/iet-rsn. 2015.0020.
[2] LI Ruiyang and HO K. Efficient closed-form estimators for multistatic sonar localization[J]., 2015, 51(1): 600-614. doi: 10.1109/TAES.2014.140482.
[3] ZEMMARI R, BROETJE M, BATTISTELLO G,. GSM passive coherent location system: Performance prediction and measurement evaluation[J].,&, 2014, 8(2): 94-105. doi: 10.1049/iet-rsn.2013.0206.
[4] DECARLI N, GUIDI F, and DARDARI D. A novel joint RFID and radar sensor network for passive localization: Design and performance bounds[J]., 2014, 8(1): 80-95. doi: 10.1109 /JSTSP.2013.2287174.
[5] 曲付勇, 孟祥伟. 基于约束总体最小二乘方法的到达时差到达频差无源定位算法[J]. 电子与信息学报, 2014, 36(5): 1075-1081. doi: 10.3724/SP.J.1146.2013.01019.
QU Fuyong and MENG Xiangwei. Source localization using TDOA and FDOA measurements based on constrained total least squares algorithm[J].&, 2014, 36(5): 1075-1081. doi: 10.3724 /SP.J.1146.2013.01019.
[6] STEIN S. Algorithms for ambiguity function processing[J].,,, 1981, 29(3): 588-599. doi: 10.1109/TASSP. 1981.1163621.
[7] TOLIMIERI R and WINOGRAD S. Computing the ambiguity surface[J].,,, 1985, 33(5): 1239-1245. doi: 10.1109/ TASSP.1985.1164688.
[8] AUSLANDER L and TOLIMIERI R. Computing decimated finite cross-ambiguity functions[J].,,, 1988, 36(3): 359-364. doi: 10.1109/29.1532.
[9] OZDEMIR A K and ARIKAN O. Fast computation of the ambiguity function and the Wigner distribution on arbitrary line segments[J]., 2001, 49(2): 381-393. doi: 10.1109/78.902121.
[10] TAO R, ZHANG W Q, and CHEN E Q. Two-stage method for joint time delay and Doppler shift estimation[J].,&, 2008, 2(1): 71-77. doi: 10.1049 /iet-rsn:20060014.
[11] SHIN D C and NIKIAS C L. Complex ambiguity functions using nonstationary higher order cumulant estimates[J]., 1995, 43(11): 2649-2664. doi: 10.1109/78.482115.
[12] NIU X, CHING P C, and CHAN Y T. Wavelet based approach for joint time delay and Doppler stretch measurements[J].and, 1999, 35(3): 1111-1119. doi: 10.1109/7. 784079.
[13] BELANGER S P. Multipath TDOA and FDOA estimation using the EM algorithm[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Minneapolis, USA, 1993: 168-171. doi: 10.1109/ICASSP.1993.319621.
[14] GILAVERT C, MOUSSAOUI S, and IDIER J. Efficient Gaussian sampling for solving large-scale inverse problems using MCMC[J]., 2015, 63(1): 70-80. doi: 10.1109/TSP.2014.2367457.
[15] BATES B C and CAMPBEL E P. A Markov chain Monte Carlo scheme for parameter estimation and inference in conceptual rainfall-runoff modeling[J]., 2001, 37(4): 937-947. doi: 10.1029/2000WR900363.
[16] 林彦, 王秀坛, 彭应宁, 等. 基于MCMC的线性调频信号最大似然参数估计[J]. 清华大学学报(自然科学版), 2004, 44(4): 511-514. doi: 10.3321/j.issn:1000-0054.2004.04.020.
LIN Yan, WANG Xiutan, PENG Yingning,. Maximum likelihood parameter estimation of chirp signals based on MCMC[J].(), 2004, 44(4): 511-514. doi: 10.3321/j.issn:1000- 0054.2004.04.020.
[17] NG W, REILLY J P, KIRUBARAJAN T,. Wideband array signal processing using MCMC methods[J]., 2005, 53(2): 411-426. doi: 10.1109/TSP.2004.838934.
[18] 李晶, 赵拥军, 李冬海. 基于马尔科夫链蒙特卡罗的时延估计算法[J]. 物理学报, 2014, 63(13): 67-73. doi: 10.7498/aps.63. 130701.
LI Jing, ZHAO Yongjun, and LI Donghai. Time delay estimation using Markov chain Monte Carlo method[J]., 2014, 63(13): 67-73. doi: 10.7498/aps.63. 130701.
[19] PINCUS M. A closed form solution of certain programming problems[J]., 1968, 16(3): 690-694. doi: 10.1287/opre.16.3.690.
Maximum Likelihood TDOA-FDOA Estimator Using Markov Chain Monte Carlo Sampling
ZHAO Yongjun ZHAO Yongsheng ZHAO Chuang
(,,450001,)
This paper investigates the joint estimation of Time Difference Of Arrival (TDOA) and Frequency Difference Of Arrival (FDOA) in passive location system, where the true value of the
ignal is unknown. A novel Maximum Likelihood (ML) estimator of TDOA and FDOA is constructed, and Markov Chain Monte Carlo (MCMC) method is applied to finding the global maximum of likelihood function by generating the realizations of TDOA and FDOA. Unlike the Cross Ambiguity Function (CAF) algorithm or the Expectation Maximization (EM) algorithm, the proposed algorithm can also estimate the TDOA and FDOA of non-integer multiple of the sampling interval and has no dependence on the initial estimate. The Cramer Rao Lower Bound (CRLB) is also derived. Simulation results show that, the proposed algorithm outperforms the CAF and EM algorithm for different SNR conditions with higher accuracy and lower computational complexity.
Passive location; Time Difference Of Arrival (TDOA); Frequency Difference Of Arrival (FDOA); Joint estimation; Maximum Likelihood (ML); Markov Chain Monte Carlo (MCMC) method
TN971
A
1009-5896(2016)11-2745-08
10.11999/JEIT160050
2016-01-13;改回日期:2016-06-08;
2016-09-01
赵拥军 zhaoyongjuntg@126.com
国家自然科学基金(61401469, 41301481, 61501513),国家高技术研究发展计划(2012AA7031015)
The National Natural Science Foundation of China (61401469, 41301481, 61501513), The National High Technology Research and Development Program of China (2012AA7031015)
赵拥军: 男,1964年生,教授,博士生导师,主要研究方向为雷达信号处理、阵列信号处理.
赵勇胜: 男,1990年生,硕士生,研究方向为无源定位.
赵 闯: 男,1978年生,教授,主要研究方向为雷达信号处理.

