基于随机摄动再采样的粒子概率假设密度滤波器

徐从安 何 友 夏沭涛 程俊图 董云龙



基于随机摄动再采样的粒子概率假设密度滤波器

徐从安*①何 友①夏沭涛①程俊图②董云龙①

①(海军航空工程学院信息融合研究所 烟台 264001)②(中国人民解放军91213部队 烟台 264000)

作为概率假设密度滤波的典型实现方式，粒子概率假设密度滤波器无需线性高斯等先验假设，因而在多目标跟踪中得到了广泛的应用。为解决粒子退化问题并保持粒子规模，该滤波器引入了重采样机制，然而，该重采样机制易引起粒子多样性耗尽，导致粒子贫化问题产生。为解决这一问题，该文提出一种新的基于随机摄动再采样的粒子概率假设密度滤波器。首先，全面分析了粒子概率假设密度滤波因粒子贫化问题导致目标失跟的过程。然后设计了一种随机摄动再采样算法，该算法在重采样导致粒子多样性缺失时，根据源粒子的位置与复制次数随机产生相应数目的新粒子，并对源粒子进行删减，其可在保留源粒子信息的前提下保持粒子的多样性。最后，该文将该算法纳入概率假设密度滤波框架，提出了一种新的粒子概率假设密度滤波器。仿真结果表明该滤波器在不显著增加运行时间的前提下能够克服粒子贫化问题，相比标准的粒子概率假设密度滤波器具有更好的跟踪性能。

多目标跟踪；概率假设密度；粒子滤波；随机摄动再采样

1 引言

在实际的目标跟踪场景中，目标的数目和状态实时变化，同时量测信息也存在很大的不确定性(目标、杂波或虚警等)，这为多目标跟踪带来了巨大挑战。如何在杂波背景下实时准确估计目标数目并进行稳定跟踪，是雷达数据处理领域的研究重点和难点问题之一。传统的多目标跟踪方法通常假定目标个数已知或未知恒定，其首先要进行数据关联，常用的数据关联方法有最近邻(Nearest Neighbor, NN)[1]，多假设跟踪(Multiple Hypothesis Tracking, MHT)[2]和联合概率数据互联(Joint Probability Data Association, JPDA)[3]等。经数据关联后，多目标跟踪问题转化为单目标跟踪问题，然后采用单目标滤波算法对目标进行滤波，经典的滤波算法主要有卡尔曼滤波(Kalman Filter, KF)[4,5]、扩展卡尔曼滤波 (Extend Kalman Filter, EKF)[6]、粒子滤波(Particle Filter, PF)等。当目标密集或者虚警较多时，基于数据关联的多目标跟踪方法往往存在组合爆炸、关联误差与状态估计相互耦合等问题，此时跟踪误差较大且实时性差。

近年来，越来越多的研究者尝试运用随机有限集(Random Finite Set, RFS)理论解决多目标跟踪问题，其中最具代表性的是文献[14]提出的概率假设密度(Probability Hypothesis Density, PHD)滤波器，该算法可避免复杂的数据关联，能够估计目标个数与状态，尤其适合解决目标数未知时变的多目标跟踪问题，具有较高的研究价值。针对PHD滤波的循环递推，为避免引入复杂的点过程理论，文献[15]从物理空间的角度进行了推导。针对PHD滤波的实现，文献[16]基于线性高斯假设提出了高斯混合PHD(Gaussian Mixture PHD, GM-PHD)滤波器，文献[17]将粒子滤波融入PHD滤波框架，提出了粒子PHD(Particle PHD, P-PHD)滤波器。与GM- PHD相比，P-PHD适用于非线性非高斯情况，因而在实际中得到了更广泛的应用。

作为PHD滤波的粒子实现形式，与PF滤波算法类似，P-PHD同样存在粒子贫化问题。为克服PF的粒子贫化问题，研究者提出了一系列解决方法。正规化粒子滤波(Regularized Particle Filter, RPF)[8]用连续函数表示后验概率密度，避免了重采样算法对离散函数采样产生的粒子多样性下降问题，但该算法在高维情况下的正则化难以实现。马尔科夫蒙特卡洛(Markov Chain Monte Carlo, MCMC)算法[9]在原重采样算法的基础上增加移动处理，减弱粒子之间的关联性，但其为保证收敛所需概率转移次数大，算法运算量大，且收敛的判断也是个问题。精选重采样(Exquisite Resampling, ER)算法[10]采用拟蒙特卡罗方法产生等间隔的粒子点，粒子点数目由复制次数决定，从而保持了重采样之后粒子集的多样性，但该方法对新生点要重新确定权值，面临计算量增大的问题。裂变自举粒子滤波 (Fission Bootstrap Particle Filter, FBPF)[11]通过权值排序、裂变繁殖等来克服样本枯竭问题，但该算法同样存在计算量大的问题。此外，机器学习、人工智能等技术也为解决PF滤波算法存在的多样性匮乏问题提供了一些新思路，文献[12]对此进行了总结。

当对PHD滤波器进行粒子实现时，并非将PF完全移植过来，在粒子重采样步，标准PF与P-PHD滤波器的差异主要体现在两方面：一是P-PHD重采样后粒子权值并不是归一化到1，而是保持权值总和不变；二是P-PHD每一迭代周期都有一部分新生粒子补充进来，若不重采样则粒子规模会不断增加，因此除消除粒子权值退化外，P-PHD重采样的另一重要目的就是控制粒子数。正是这种差异性的存在，现有解决PF滤波算法粒子贫化问题的方法在推广至PHD滤波框架下时仍存在局限性(无法推广、计算量大等)，因而目前还未见文献对该问题进行专门研究。本文在全面分析P-PHD滤波器粒子贫化问题可能导致目标失跟的基础上，提出了一种随机摄动再采样算法，并将该算法融入PHD滤波框架，提出了一种新的P-PHD(Stochastic Perturbation P-PHD, SPP-PHD)滤波器并给出了其具体实现过程。

2 P-PHD滤波器的粒子贫化问题

同PF类似，在标准P-PHD滤波器中，为避免粒子退化引入了重采样机制，其主要思想为集中权值较高的粒子，淘汰权值较低的粒子。然而，由于较高权值粒子被大量复制，较低权值粒子逐渐消失，经若干次迭代后会导致“粒子坍塌”(particle collapse)，即所有粒子都坍塌到某一个或某几个点上，从而导致粒子多样性不足，以至于剩余粒子不能准确描述后验概率密度函数，这一问题被称为粒子贫化问题。

为更形象地描述这一问题，图1给出了P-PHD滤波器经重采样后粒子的演化过程，图中代表粒子的圆越大，表明对应粒子权值越大，复制次数越多。由图1可以看出，在P-PHD滤波初期的第步，大量权值相近的粒子围绕在真实目标附近，随着PHD的不断迭代更新，粒子多样性逐渐降低，当进行到第步时，出现了“粒子坍塌”现象，仅剩两种粒子来对后验概率密度进行描述，若此时再进行下一步迭代到步，粒子很可能完全丢失，从而导致P-PHD无法跟踪目标。需要说明的是，若用标准PF来对目标进行跟踪时，当迭代到步时粒子个数并不会减少，但粒子并不聚集在目标周围，而P-PHD则可能导致粒子丢失，这也正是两种算法重采样的差异所在。

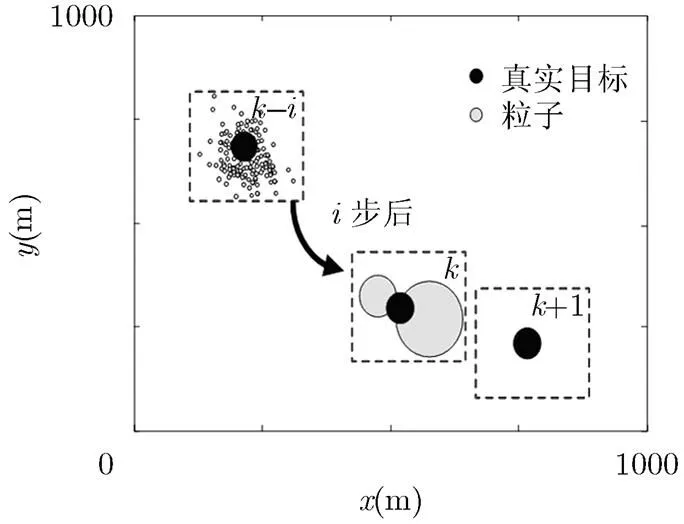
图1 P-PHD滤波器重采样后粒子的演化过程

由以上对粒子演化过程的分析可以看出，重采样过程虽避免了粒子退化，但同时带来了粒子贫化问题。为解决这一问题，可通过增加粒子数提高粒子多样性，但这会带来计算量的提升。如何在不显著提高算法计算量的前提下，克服P-PHD滤波器因粒子贫化问题带来的目标失跟，是一个很有意义且亟待解决的问题。

3 SPP-PHD滤波器

为解决P-PHD滤波器的粒子贫化问题，考虑从粒子贫化问题产生的根源对P-PHD进行改进。由前分析可知，粒子贫化问题是由P-PHD滤波器重采样步对高权值粒子的过度复制引起的，为此设计一种随机摄动再采样算法，当粒子多样性缺失时，将重采样粒子作为源粒子，根据源粒子位置和复制次数随机产生新粒子，并对源粒子进行删减，在保留重采样粒子信息的同时保持粒子多样性。然后，在P-PHD重采样后加入该随机摄动再采样算法，将其纳入P-PHD滤波框架，得到SPP-PHD滤波器。

3.1随机摄动再采样算法

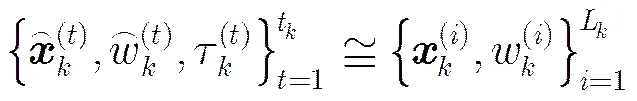
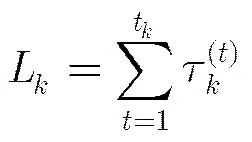
为增加粒子的多样性，考虑对粒子进行再采样，但若对所有粒子都进行再采样，将会增加计算量。为此，随机摄动再采样算法首先对粒子进行多样性判断，以决定是否需要进行再采样操作。作如下定义：若

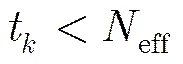
则称重采样粒子多样性不足，反之则为粒子多样性充足。需要说明的是，的取值是由经验确定的，此处参考文献[13]取。

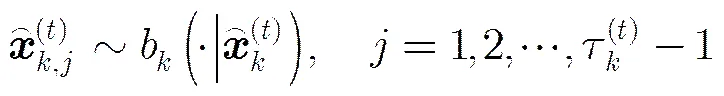
其中，

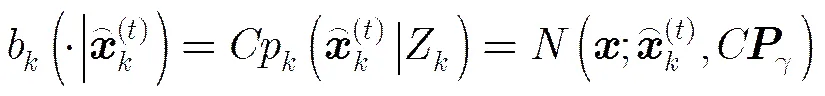
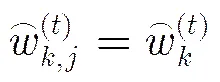
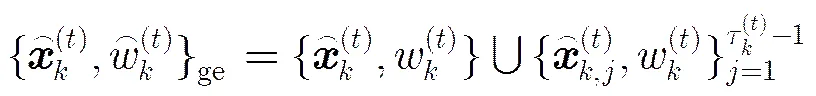
故所有基于源粒子随机摄动得到的粒子集合为

由式(7)可知，在随机摄动再采样操作中，新粒子个数取决于源粒子的复制次数，而所有源粒子仅被保留1次。这样，在这一过程中，粒子总数并没有发生变化，在保留源粒子信息的前提下，通过删减源粒子复制次数并生成新粒子增加了粒子的多样性。下面将随机摄动再采样算法的步骤总结如下：

步骤 1 在重采样过程中设置标签计数器，记录每个源粒子复制次数；

步骤3 根据式(3)进行粒子多样性判断，若粒子多样性充足，则，反之则进行后续步骤；

3.2 SPP-PHD滤波器

将上述随机摄动再采样算法纳入PHD滤波框架，便得到SPP-PHD滤波器。对于SPP-PHD滤

4 仿真实验与结果分析

为验证SPP-PHD滤波器解决粒子贫化问题的有效性，本文在不同实验条件下进行性能仿真，并同P-PHD进行对比分析，实验中目标作转弯速率未知的匀速转弯运动。

表1 时刻SPP-PHD滤波器实现伪代码

表1 时刻SPP-PHD滤波器实现伪代码

输入：(1)时刻粒子集：；(2)时刻量测集预测： for do 采样，预测权值 end for fordo 采样，预测权值 end for更新： fordo参照P-PHD滤波器更新权值end for重采样：计算目标数估计对粒子集重采样得，并设置粒子复制次数的标签Index随机摄动再采样(粒子删减与生成)：根据重采样中设置的标签得粒子复制次数，将粒子集重写成if do for do for do根据复制次数生成新粒子end for通过式(7)计算由源粒子生成的粒子集end for通过式(8)得随机摄动再采样后的粒子集else do随机摄动再采样后的粒子集 end if状态估计：采用粒子集进行状态估计，得状态估计集合输出：(1)目标数估计；(2)经随机摄动再采样后粒子集；(3)状态估计集合

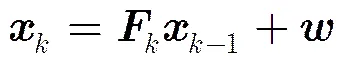
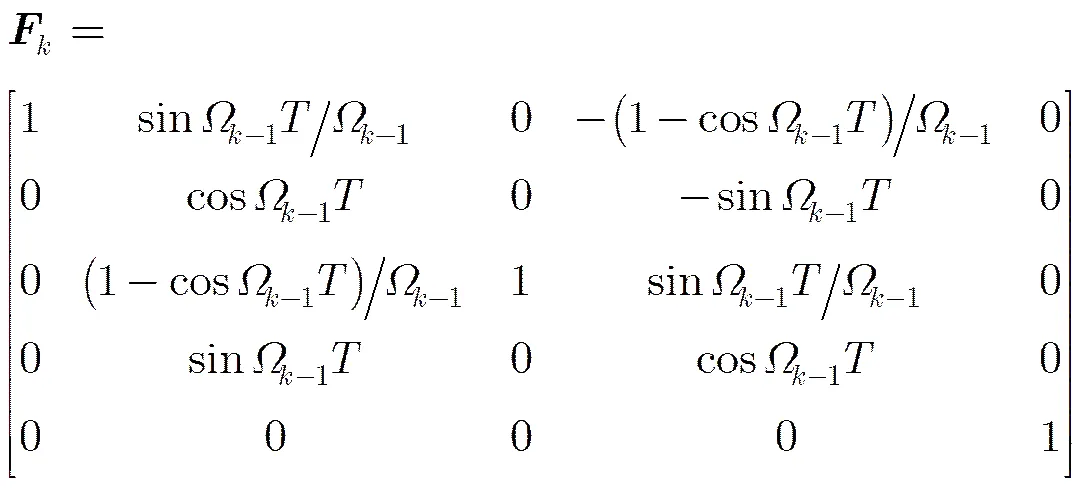
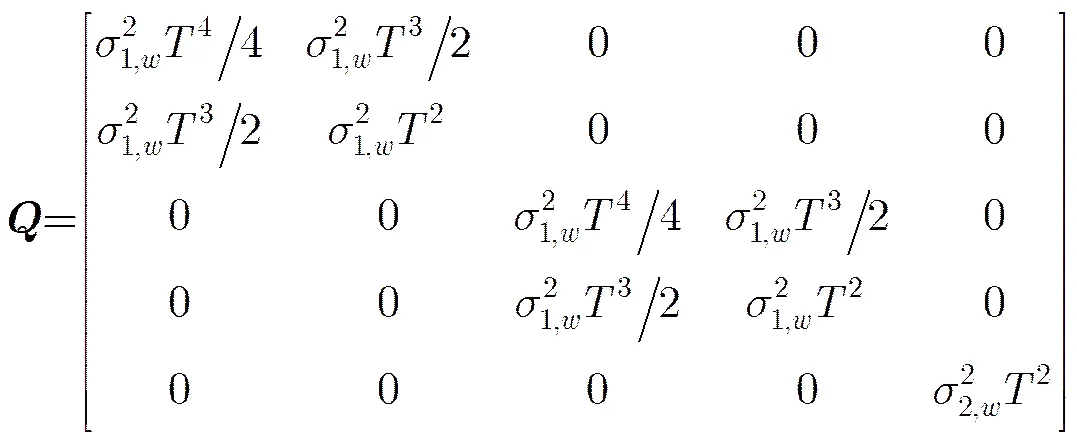
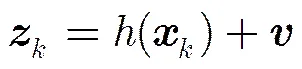
若杂波模型服从泊松点过程，其强度为

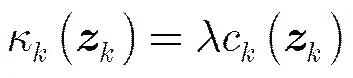
新生目标的PHD为

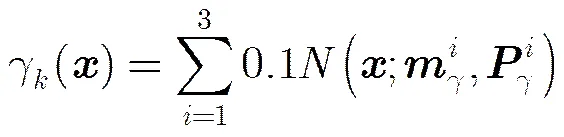
图2为目标真实运动轨迹，“○”表示目标出生位置，“□”表示目标消亡位置。目标1第2 s新生，第76 s消亡；目标2第15 s新生，第60 s消亡；目标3第40 s时新生，第100 s消亡；目标4第15 s新生，第60 s消亡。

图3表示P-PHD和SPP-PHD滤波器单次试验的多目标位置估计。由图3可以看出，SPP-PHD由于采用了随机摄动再采样算法，增加了粒子多样性，克服了粒子贫化问题，能有效地跟踪所有目标，而P-PHD则因粒子贫化问题漏掉了目标2和目标3。同时，对比图3(a)和图3(b)可以看出，对于目标1和目标4，两滤波器估计精度相近，这说明在不发生粒子贫化时，SPP-PHD并不降低目标位置估计精度。

图4表示经50次MC实验P-PHD和SPP-PHD滤波器的目标个数估计平均。由图4可以看出，SPP-PHD由于采用了随机摄动再采样算法，有效克服了粒子贫化问题，目标个数估计精度明显优于P-PHD，且随着真实目标数的增多，SPP-PHD滤波器的估计优势越明显。特别地，当真实目标数为4时，P-PHD目标估计相比SPP-PHD低约2，这是由于P-PHD因粒子贫化问题导致目标漏估，目标数越多，发生粒子贫化的可能性越大，目标漏估越多，而SPP-PHD由于采用了随机摄动再采样算法，有效克服了因粒子贫化导致的目标漏估现象。

为更好的对P-PHD和SPP-PHD的性能进行评估，本文采用OSPA距离[24]来度量两者的跟踪误差。对于任意两个有限集和，若, OSPA距离可定义为

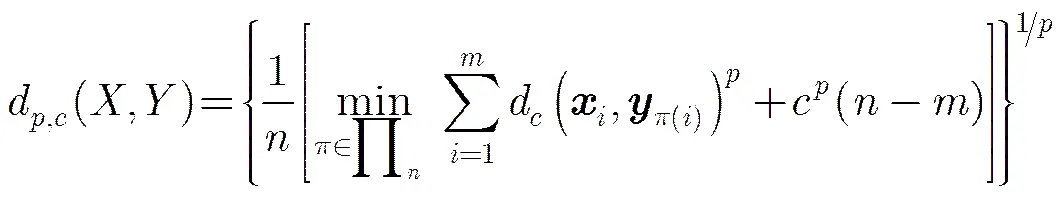
图5表示经50次MC实验P-PHD和SPP-PHD滤波器的平均OSPA距离估计。由图5可以看出，随着跟踪步数的增加，SPP-PHD算法的OSPA距离变化不大，基本维持在10 m到12 m之间，而P-PHD算法的OSPA则大幅上升直至40 m左右，即SPP-PHD算法的位置估计精度明显优于SPP- PHD。同时，随着真实目标数的增加，两滤波器OSPA均有所增加，但SPP-PHD增加幅度小于P- PHD，这说明随着目标数的增加，SPP-PHD相比P-PHD估计优势更为明显。

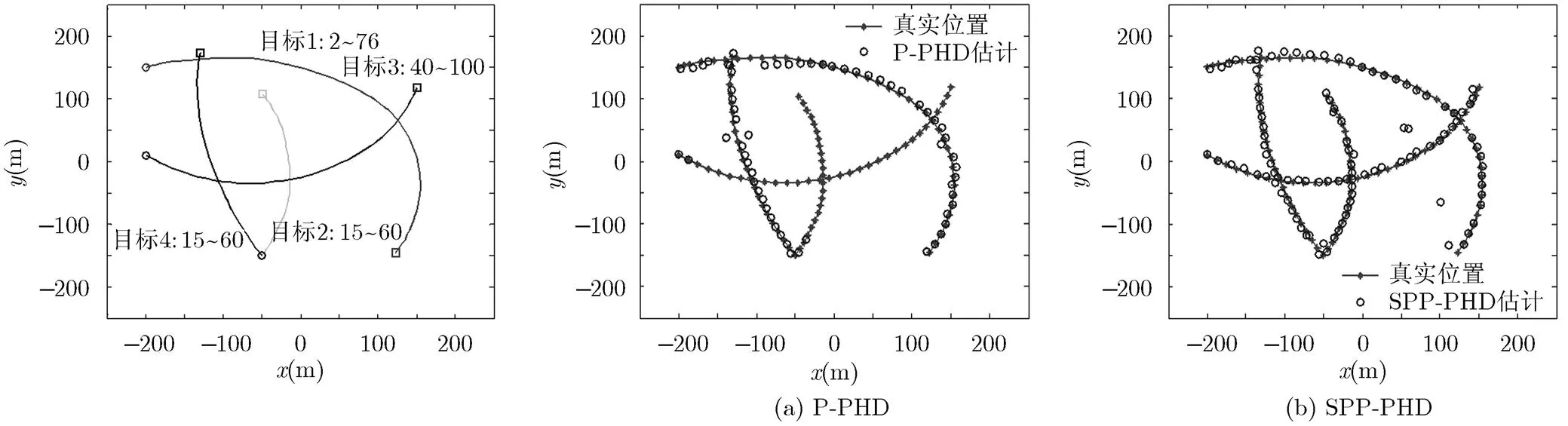
图2 目标真实运动轨迹           图3 单次实验的多目标位置估计

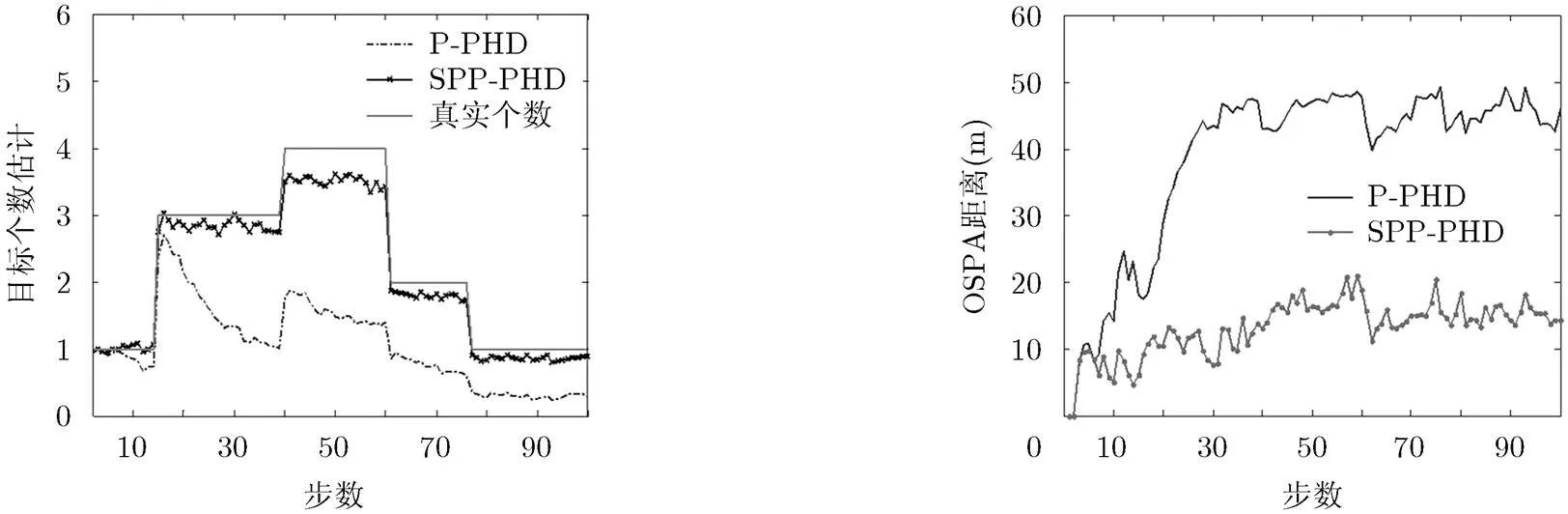
图4 目标个数估计(50次MC平均)           图5 OSPA距离估计(50次MC平均)

由于计算机性能的差异，算法实际运行时间存在差异，故本文在进行运行时间对比时采用归一化时间来表示。表2给出了50次实验P-PHD和SPP-PHD滤波器的归一化平均运行时间(以P-PHD为标准)。由表2可以看出，SPP-PHD与P-PHD运行时间差别很小。结合图5可知，SPP-PHD在几乎不提高运行时间的同时能够大幅提高算法的性能。

表2 50次实验P-PHD和SPP-PHD的平均运行时间

5 结论

本文设计了一种随机摄动再采样算法，该算法为保持粒子多样性，在粒子重采样结束后根据源粒子的位置与复制次数随机产生相应数目的新粒子，并对源粒子进行删减。同时在对粒子贫化问题进行分析的基础上，将该算法纳入P-PHD框架，提出了一种新的滤波器SPP-PHD，旨在解决P-PHD算法的粒子贫化问题。仿真实验表明，相比P-PHD算法，本文算法在不显著增加运行时间的前提下能够有效解决粒子贫化问题，具有更好的跟踪性能。

[1] BAR-SHALOM Y and FORTMANN T E. Tracking and Data Association[M]. Boston: Academic Press, 1988: 32-36.

[2] BLACKMAN S S. Multiple hypothesis tracking for multiple target tracking[J]., 2004, 19(1): 5-18. doi: 10.1109/MAES. 2004.1263228.

[3] FORTMANN T E, BAR-SHALOM Y, and SCHEFFE M. Sonar tracking of multiple targets using joint probabilistic data association[J]., 1983, 8(3): 173-184. doi: 10.1109/JOE.1983.1145560.

[4] KALMAN R E. A new approach to linear filtering and prediction problems[J]., 1960, 82(2): 95-108.

[5] 何友, 修建娟, 关欣, 等. 雷达数据处理及应用[M]. 第3版. 北京: 电子工业出版社, 2013: 31-35.

HE You, XIU Jianjuan, GUAN Xin,. Radar Data Processing with Applications[M]. Third Edition. Beijing: Publishing House of Electronics Industry, 2013: 31-35.

[6] BUCY R S and SENNE K D. Digital synthesis of nonlinear filters[J]., 1971, 7(3): 287-298. doi: 10.1016/0005- 1098(71)90121-X.

[7] CARP J, CLIFFORD P, and FEARN P. Improved particle filter for nonlinear problems[J]., 1999, 146(1): 1-7. doi: 10.1049/ip-rsn:19990255.

[8] ARULAMPALAM M S, MASKELL S, GORDON N,. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]., 2002, 50(2): 174-188. doi: 10.1109/78.978374.

[9] SPALL J C. Estimation via markov chain monte carlo[J]., 2003, 23(2): 34-45. doi: 10.1109/MCS.2003.1188770.

[10] FU Xiaoyan and JIA Yingmin. An improvement on resampling algorithm of particle filters[J]., 2010, 58(10): 5414-5420. doi: 10.1109/ TSP.2010.2053031.

[11] 程水英, 张剑云. 裂变自举粒子滤波[J]. 电子学报, 2008, 36(3): 500-504.

CHENG Shuiying and ZHANG Jianyun. Fission bootstrap particle filtering[J]., 2008, 36(3): 500-504.

[12] 程水英, 张剑云. 粒子滤波评述[J].宇航学报, 2008, 29(4): 1099-1111.

CHENG Shuiying and ZHANG Jianyun. Review on particle filters[J]., 2008, 29(4): 1099-1111.

[13] 张琪, 乔玉坤, 孔祥玉, 等. 随机摄动强跟踪粒子滤波算法[J]. 物理学报, 2014, 63(11): 1-7. doi: 10.7498/aps.63.110505.

ZHANG Qi, QIAO Yukun, KONG Xiongyu,. Study on stochastic perturbation strong tracking particle filter[J]., 2014, 63(11): 1-7. doi: 10.7498/aps. 63. 110505.

[14] MAHLER R. Multi-target Bayes filtering via first-order multi-target moments[J]., 2003, 39(4): 1152-1178. doi: 10.1109/ TAES.2003.1261119.

[15] 翟岱亮, 雷虎民, 李海宁, 等. 概率假设密度滤波的物理空间意义[J]. 物理学报, 2014, 63(20): 1-6. doi: 10.7498/aps. 63.200204.

ZHAI Dailiang, LEI Humin, LI Haining,Derivation of the probability hypothesis density filter via the physical- space approach[J]., 2014, 63(20): 1-6. doi: 10.7498/aps.63.200204.

[16] VO B N and MA W K. The Gaussian mixture probability hypothesis density filter[J]., 2006, 54(11): 4091-4104. doi: 10.1109/TSP.2006. 881190.

[17] VO B N, SINGH S, and DOUCET A. Sequential Monte Carlo methods for Bayesian multi-target filtering with random finite sets[J]., 2005, 41(4): 1224-1245. doi: 10.1109/TAES.2005. 1561884.

[18] WU Xinhui, HUANG Gaoming, and GAO Jun. Particle filters for probability hypothesis density filter with the presence of unknown measurement noise covariance[J]., 2013, 26(6): 1517-1523. doi: 10.1016/j.cja. 2013.10.007.

[19] 徐从安, 刘瑜, 熊伟, 等. 新生目标强度未知的双门限粒子PHD滤波器[J]. 航空学报, 2015, 36(12): 3957-3966.doi: 10.7527/S1000-6893.2015.0104.

XU Cong’an, LIU Yu, XIONG Wei,. A dual threshold particle phd filter with unknown target birth intensity[J]., 2015, 36(12): 3957-3966.doi: 10.7527/S1000-6893.2015.0104.

[20] FRANCESCO P and DU Y K. A particle multi-target tracker for superpositional measurements using labeled random Finite sets[J]., 2015, 63(16): 4348-4358. doi: 10.1109/TSP.2015. 2443727.

[21] YOHAN P, MARK M, FRANCOIS D,. Marginalized particle phd filters for multiple object bayesian filtering[J]., 2014, 50(2): 1182-1196. doi: 10.1109/TAES.2014.120805.

[22] LI Tiancheng, SUN Shudong, SATTAR T P,. High-speed Sigma-gating SMC-PHD filter[J]., 2013, 93(3): 2586-2593.doi: 10.1016/j.sigpro.2013.03.011.

[23] LI Bo. Multiple-model Rao-blackwellized particle probability hypothesis density filter for multitarget tracking[J]., 2015, 13(2): 426-433. doi: 10.1007/s12555-014-0148-7.

[24] SCHUHMACHER D, VO B T, and VO B N. A consistent metric for performance evaluation of multi-object filters[J]., 2008, 56(8): 3447-3457. doi: 10.1109/TSP.2008.920469.

Particle Probability Hypothesis Density Filter Based on Stochastic Perturbation Re-sampling

XU Cong’an①HE You①XIA Shutao①CHENG Juntu②DONG Yunlong①

①(,,264001,)②(. 91213,264000,)

As a typical implementation of the Probability Hypothesis Density (PHD) filter, Particle PHD (P-PHD) is suitable for highly nonlinear systems and widely used in Multi-Target Tracking (MTT). However, the resampling in P-PHD filter, recommended to avoid particle degeneracy, introduces the problem of diversity loss among the particles, namely particle impoverishment problem. To solve the problem and improve the performance of the P-PHD filter, a novel filter based on stochastic perturbation re-sampling is proposed. First, a comprehensive analysis on the particle impoverishment problem of P-PHD filter is presented. Then for the purpose of keeping the particle diversity, a new stochastic perturbation re-sampling algorithm is developed, which generates new particles according to the position and duplicating times of the original particles, and removes some excessive copied particles. Finally, the re-sampling algorithm is integrated into the P-PHD filter framework and a Stochastic Perturbation Particle PHD (SPP-PHD) filter is proposed. Numerical examples show that the proposed filter can overcome the particle impoverishment problem and improve the estimation performance on the premise of not significantly improving the simulation time.

Multi-Target Tracking (MTT); Probability Hypothesis Density (PHD); Particle Filter (PF); Stochastic perturbation re-sampling

TN391

A

1009-5896(2016)11-2819-07

10.11999/JEIT160114

2016-01-26；改回日期：2016-07-08；

2016-09-30

徐从安 xcatougao@163.com

国家自然科学基金 (61471383, 61304103)

The National Natural Science Foundation of China (61471383, 61304103)

徐从安： 男，1987年生，博士，讲师，主要研究方向为多目标跟踪、随机集理论等.

何 友： 男，1956年生，博士，教授，中国工程院院士，博士生导师，主要研究方向为多传感器信息融合、雷达数据处理、系统建模仿真等.

夏沭涛： 男，1978年生，硕士，工程师，主要研究方向为通信系统仿真建模.

程俊图： 男，1985年生，工程师，主要研究方向为系统建模仿真.

董云龙： 男，1974年生，博士，副研究员，主要研究方向为多传感器信息融合.